УДК 537.874.31

ИССЛЕДОВАНИЕ ПЛАЗМОННОГО РЕЗОНАНСА НА МЕДНОЙ ПЛЕНКЕ, НАПЫЛЕННОЙ НА СВЕТОВОД С НАКЛОННОЙ БРЭГГОВСКОЙ РЕШЕТКОЙ

 

И. А. Нечепуренко ^1,2, А. В. Дорофеенко ^1,2,3, К. А. Томышев ⁴, О. В. Бутов⁴

¹ Всероссийский научно-исследовательский институт автоматики им. Н.Л. Духова,
² Московский физико-технический институт (Государственный университет),

³ Институт теоретической и прикладной электродинамики РАН

⁴ Институт радиотехники и электроники им. В.А. Котельникова РАН

 

Статья получена 1 апреля 2015 г.

 

Аннотация. Экспериментально реализован метод возбуждения плазмонного резонанса на медной пленке, напыленной на поверхность световода с записанной в нем наклонной брэгговской решеткой. Найдено объяснение исчезновения четкого плазмонного резонанса в спектре прохождения системы. Показано, что в течение нескольких часов после нанесения пленки плазмонный резонанс испытывает красное смещение и претерпевает уширение, вплоть до полного исчезновения резонанса. Эти эффекты хорошо согласуются с расчетом, в котором учтена деградация слоя меди. Найдено характерное время, в течение которого медная пленка сохраняет плазмонные свойства.

Ключевые слова: плазмонный волоконнооптический датчик показателя преломления, наклонная брэгговская решетка, оболочечные моды оптического волновода.

Abstract. A method of surface plasmon resonance excitation in a copper film deposited onto a lateral surface of fiber, which contains a tilted fiber Bragg grating in its core, is realized experimentally. A reason for disappearance of distinct plasmon resonance is determined. It is shown that within some hours after the film deposition plasmon resonance is subject to redshift, accompanied by broadening, which leads to the resonance evanescence. These effects are in good agreement with calculation, which takes the copper degradation into account. A characteristic lifetime of the copper film is found.

Keywords: plasmonic optical fiber sensor of refractive index, tilted fiber Bragg grating, fiber cladding modes.

 

Введение

Возбуждение плазмонного резонанса на металлизированной поверхности диэлектрика в плоской (призма) или цилиндрической (световод) геометрии позволяет сделать систему высокочувствительной к параметрам внешней среды. Это, в свою очередь, открывает возможность создания сенсоров на основе подобных систем.

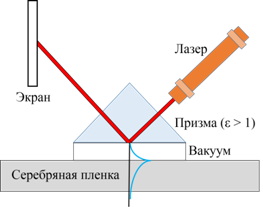
В основе такого рода устройств лежат схемы, предложенные Кречманном [1] и Отто [2], (рис. 1а, б). Схема Кречманна является более удобной для сенсорных применений, и именно она служит прообразом рассматриваемой здесь схемы. Суть методики заключается в следующем. Пучок, падающий через призму с диэлектрической проницаемостью , основание которой покрыто металлической пленкой, испытывает полное внутреннее отражение от исследуемого материала, находящегося с внешней стороны пленки (рис. 1а). При углах, больших угла полного внутреннего отражения (ПВО) от границы призма/вакуум, в гипотетическом случае отсутствия потерь коэффициент отражения равен единице. Однако такая система содержит скрытую особенность: при определенном угле падения наблюдается резкое возрастание интенсивности поля вблизи границы металла. Поэтому в реальной ситуации, благодаря потерям в металле, вблизи этого угла наблюдается рост поглощения и возникает резкий минимум коэффициента отражения (рис. 2). Это явление принято называть нарушенным полным внутренним отражением (НПВО). Положение минимума крайне чувствительно к свойствам исследуемого материала. Таким образом, по положению минимума можно определить диэлектрическую проницаемость среды, граничащей с металлом.

 

а	б
Рисунок 1. Схемы Кречманна (а) и Отто (б). Синяя линия – распределение интенсивности поля плазмона.

 

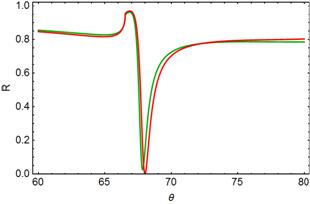
Рисунок 2. Коэффициенты отражения от призмы в схеме Кречманна для p-поляризации. Коэффициент отражения рассчитан для слоя золота толщиной 36 нм (красная кривая) и слоя меди той же толщины (зеленая кривая).

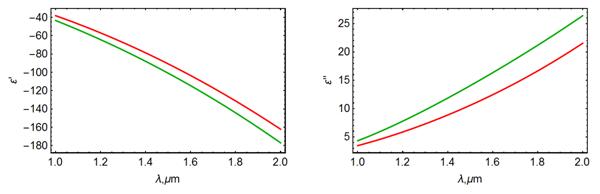
Обычно в качестве материала, обеспечивающего распространение плазмонов, используется золото. Тем не менее, дисперсии золота и меди в ближней ИК-области, часто используемой в волоконных схемах, практически совпадают (рис. 3а, б). Соответственно, спектры отражения плазмонных систем, содержащих золото и медь, также должны быть близки (см. рис. 2). Однако результатов, полученных с использованием медных пленок, в литературе встречается относительно немного [3, 4], что, вероятно, связано с меньшей химимической стабильностью данного материала.

 

а)                                                           б)

Рисунок 3. Дисперсия дейсвительной (а) и мнимой (б) частей диэлектрической проницаемости
золота (красные линии) и меди (зеленые линии).

Волоконно-оптический плазмонный датчик с наклонной брэгговской решеткой

На основе предложенной Кречманном схемы возникли и различные реализации, позволяющие резонансно усилить поле на границе металлической пленки. Одной из наиболее перспективных для приложений является схема на основе оптического волокна, реализованная и исследованная в ряде недавних работ [5-16]. Насколько нам известно, во всех подобных работах в качестве металла используется золото, и лишь в работе [8] исследуется композит из медных наночастиц. В нашей работе схема на оснве волокна с наклонной брэгговской решеткой впервые реализована с использованием сплошного медного напыления.

Рассматриваемая система представляет собой кварцевый волоконный световод, состоящий из тонкой одномодовой сердцевины диаметром 8-9 мкм и светооотражающей оболочки с внешним диаметром 125 мкм, на которую нанесена металлическая пленка толщиной 30-60 нм (рис 4). На участке сердцевины волоконного световода длиной около 10 мм записана периодическая структура в виде наклонной брэгговской решетки с углом наклона 9.5⁰ по отношению к плоскости, перпендикулярной оси световода (см., например, [7, 9]). Оптический сигнал, распространяющийся по сердцевине световода, попадает на брэгговскую решетку, на которой происходит рассеяние света с возбуждением мод, распространяющихся в оболочке оптоволокна и взаимодействующих с металлической пленкой и внешней средой.

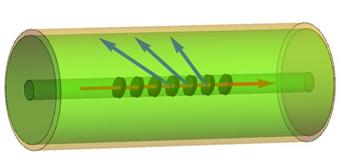
Рисунок 4. Схема плазмонного датчика показателя преломления на основе оптического волоконного световода,
содержащего наклонную брэгговскую решетку.

Локализация моды сердцевины обеспечивается полным внутренним отражением от границы сердцевина-оболочка. Моды оболочки же испытывают полное внутреннее отражение от внешней границы оболочки. Это означает, что дисперсионные кривые мод оболочки лежат в области между световыми конусами, соответствующими внешней среде () и материалу оболочки (стекло, ), см. рис. 5. Здесь  и  – показатели преломления внешней среды и оболочки соответственно. Дисперсионная кривая моды сердцевины, в свою очередь, проходит между световыми конусами оболочки и сердцевины. В реальной системе коэффициент преломления сердцевины  отличается от  на величину порядка . Поэтому дисперсию моды сердцевины можно аппроксимировать дисперсией волны в материале волокна (стекле), пренебрегая отличием между оболочкой и сердцевиной:

                                              ,                                                  
где  – волновое число моды сердцевины.

Резонансное взаимодействие моды сердцевины с брэгговским зеркалом сводится к перебросу дисперсионной кривой на постоянную обратной решетки , где  – период брэгговской решетки (рис 5, красная штриховая линия). Частота, соответствующая пересечению полученной кривой с дисперсионной кривой моды, бегущей по сердцевине в обратном направлении (показана синей линией на рис. 5), есть частота брэгговского отражения в моду сердцевины. На этой частоте наблюдается резкий минимум коэффициента прохождения (вблизи  нм на рис. 6). Сказанное означает, что волновое число  в 2 раза больше волнового числа моды сердцевины, испытывающей брэгговское отражение (условие Брэгга). Зная длину волны брэгговского резонанса, находим постоянную обратной решетки:

                                             .                                                  

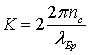На более высоких частотах (меньших длинах волн) кривая последовательно пересекает различные моды оболочки, что соответствует системе провалов в спектре прохождения (рис. 6).

 

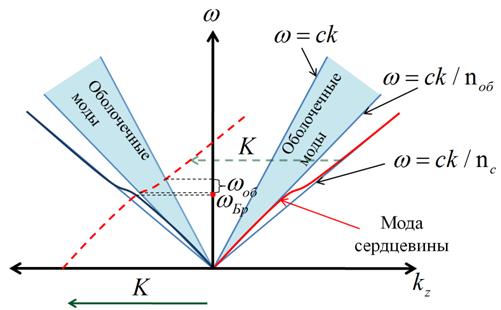
Рисунок 5. Взаимодействие мод на языке дисперсионных кривых.
Красная линия соответствует дисперсионной кривой сердцевины;
темная область заполнена дисперсионными кривыми мод оболочки,
 здесь  – тангенциальная компонента волнового вектора,  – частота брэгговского резонанса,
 – область частот, в которой расположены резонансы, связанные с оболочечными модами.

 

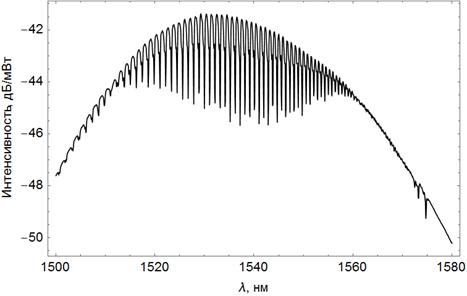
Рисунок 6. Спектр прохождения через оптическое оптоволокно, содержащее брэгговскую решетку
 с наклоном  в своей сердцевине, помещенное в воду. Диаметры сердцевины и оболочки  мкм и  мкм,
показатели преломления , , толщина металлической пленки 30-60 нм.

Условие резонансного взаимодействия мод сердцевины и оболочки получается подстановкой волнового числа  в условие переброса  ( – волновое число моды оболочки). Таким образом, в спектре прохождения моды сердцевины проявляются моды оболочки, волновое число которых связано с частотой соотношением

                                          .                                              

Возбуждение плазмонного резонанса

Для возбуждения плазмонного резонанса в системе на боковую поверхность волоконного световода был нанесен тонкий слой меди. Для нанесения использовался метод термического испарения металла в вакууме. С помощью специально разработанного механизма, в процессе напыления металла световод вращался вдоль своей оси, что обеспечивало равномерное осаждение по всей поверхности покрываемого участка оптического волокна.

При наличии металлического слоя на поверхности диэлектрического волновода происходит возбуждение отдельными оболочечными модами плазмонного резонанса на границе металл/внешняя среда. Результатом резонанса является существенное изменение интенсивности поля вблизи этой границы и резкое уменьшение длины пробега соответствующих оболочечных мод.

Возбуждение плазмонного резонанса происходит при условии равенства волновых чисел оболочечной моды и плазмона: , где

 .

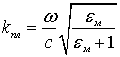 Равенство волновых чисел выполняется с точностью до ширины плазмонного резонанса: . В пределах этой ширины находится несколько оболочечных мод. Их резонансное взаимодействие с модой сердцевины гасится в результате поглощения, и система провалов в спектре прохождения моды сердцевины размывается, образуя «перетяжку» (рис. 7). Это позволяет определить положение плазмонного резонанса.

 

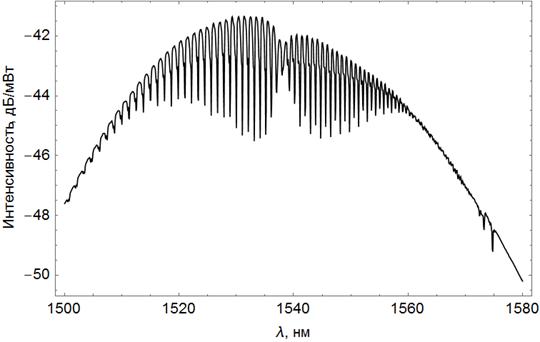
Рисунок 7. Интенсивность сигнала, прошедшего через оптоволокно, содержащее наклонную брэгговскую решетку
с наклоном  в своей сердцевине, покрытое слоем меди толщиной 33 нм.

Изменение внешнего показателя преломления приводит к смещению положения плазмонного резонанса и, как следствие, к смещению перетяжки в спектре прохождения. Смещение перетяжки может быть использовано для определения внешнего показателя преломления с точностью до . Заметим, что ширина плазмонного резонанса на медной пленке составляет примерно 10 нм, что совпадает с характерной шириной плазмонных резонансов, полученных при использовании золотой пленки (см. например [14]). Таким образом, плазмонный резонанс на медной пленке, нанесенной на оптическое волокно, оказывается достаточно узким, что позволяет ожидать высокой точности измерения показателя преломления [7].

 

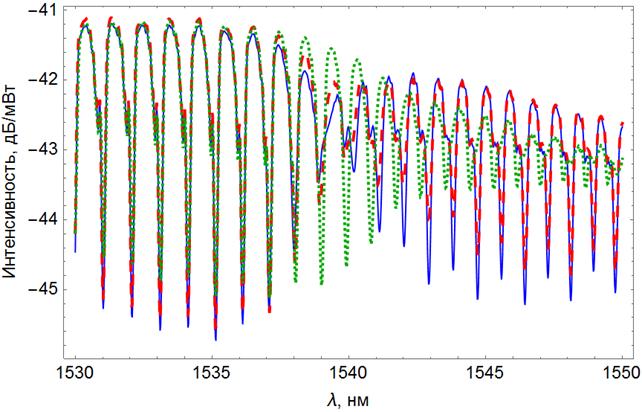
Рисунок 8. Спектральная зависимость интенсивности света, прошедшего через оптоволокно,
содержащее наклонную брэгговскую решетку с наклоном  в своей сердцевине,
покрытое слоем меди, толщиной 33 нм. Сплошная синяя, штриховая красная и пунктирная зеленая кривые
 получены, соответственно, через 35, 205 и 395 минут после нанесения медной пленки.
Измерения спектра проводились при погружении волокна в изопропиловый спирт.

Для исследования поведения плазмонного резонанса при химической деградации медной пленки были проведены измерения спектра прохождения в разные моменты времени в течение нескольких часов после нанесения пленки. Измерения проводились при погружении участка световода с медной пленкой в концентрированный раствор изопропилового спирта. В промежутках между измерениями сенсор находился в воздухе. Существенное изменение спектра происходило за время порядка 2–3 часов после нанесения пленки (рис 8). В течение этого времени наблюдается уширение резонанса с небольшим сдвигом вправо по оси длин волн.

Для анализа наблюдаемых эффектов были численно определены верхняя и нижняя огибающие спектров на рис. 8. Разность значений, соответствующих этим огибающим, дает представление о параметрах плазмонного резонанса – его частоте и ширине (рис. 9).

 

  

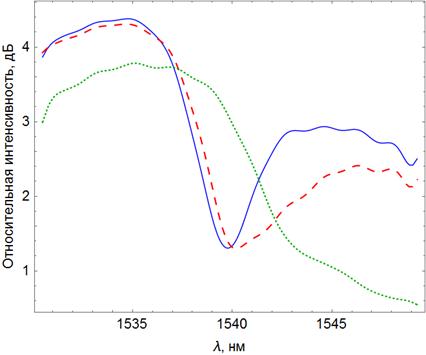
Рисунок 9. Профиль плазмонного резонанса на меди, толщиной 33 нм.
Сплошная синяя кривая – сигнал, измеренный через 35 минут после напыления,
штриховая красная кривая – сигнал, измеренный через 205 минут и
пунктирная зеленая кривая – сигнал, измеренный через 395 минут.

Уширение плазмонного резонанса в процессе деградации медной пленки связано с ростом потерь, которые могут быть вызваны рассеянием волны на неоднородностях, образующихся в результате окисления меди. Качественное описание процесса деградации медной пленки возможно путем сравнения параметров плазмонного резонанса (частоты и ширины) с аналогичными параметрами, рассчитанными для схемы Кречманна. Чтобы это сравнение было корректным, сканирование длины волны в схеме Кречманна должно сопровождаться одновременным изменением угла падения  таким образом, чтобы тангенциальное волновое число падающего луча  было равно волновому числу оболочечной моды, определенной по формуле , т.е. , где  находится по формуле . Коэффициент отражения, соответствующий табличным значениям диэлектричной проницаемости меди [17], показан синей кривой на рис. 10. Сравнение синих кривых на рис. 9 и 10 показывает, что расчет неплохо предсказывает экспериментально наблюдаемое положение плазмонного резонанса и его ширину.

Для описания наблюдаемого со временем уширения плазмонного резонанса (штриховая красная и пунктирная зеленая кривые на рис. 9) в расчете была увеличена мнимая часть диэлектрической проницаемости меди. Независящая от частоты мнимая добавка к диэлектрической проницаемости, равная , позволила описать наблюдаемое двукратное увеличение ширины резонанса (штриховая красная кривая на рис. 10). Описание дальнейшего размытия резонанса потребовало увеличения мнимой части диэлектрической проницаемости меди вплоть до значения действительной части, что может соответствовать нарушению однородности слоя в следствии неоднородности процесса окисления меди.

Естественно, в отсутствие плазмонной перетяжки работа датчика становится невозможной. По результатам наблюдений, характерное время эффективного функционирования датчика с медным напылением составило примерно 200 минут при проведении измерений с применением изопропилового спирта. Очевидно, что полученное характерное время зависит от условий и окружающей среды, в которых проводился эксперимент. Тем не менее, временя жизни медной пленки может быть увеличено, например, путем нанесения тонкого полимерного покрытия или стойкого к химическому воздействию металлического покрытия.

 

 

Рисунок 10 Коэффициент отражения для схемы Кречманна с медной пленкой.
Сплошная синяя кривая соответствует табличной дисперсии меди,
штриховая красная и пунктирная зеленая кривые – увеличению мнимой части
диэлектрической проницаемости меди на 25 и на 80, соответственно.

Заключение

В работе впервые наблюдался плазмонный резонанс на однородной медной пленке, нанесенной на боковую поверхность волоконного световода с наклонной брэгговской решеткой. По изменению спектральных характеристик плазмонного резонанса изучена динамика деградации слоя меди. Экспериментальные данные хорошо согласуются с теоретическими расчетами, основанными на предположении неравномерного разрушения медного покрытия, например, вследствие его окисления или частичного растворения. Время деградации пленки, естественно, зависит от окружающей среды, в которой проводились измерения.

Работа выполнена при финансовой поддержке Фонда перспективных исследований (контракт номер 7/004/2013-2018 от 23.12.2013) и Российского фонда фундаментальных исследований.

Литература

[1]     E. Kretschmann, "Die Bestimmung optischer Konstanten von Metallen durch Anregung von Oberflachenplasrnaschwingungen," Z. Physik, vol. 241, pp. 313-324, 1971.

[2]     A. Otto, "Excitation of nonradiative surface plasma waves in silver by the method of frustrated total reflection," Z Physik, vol. 216, pp. 398-410, 1968.

[3]     M. Mitsushio, K. Miyashita, M. Higo, "Sensor properties and surface characterization of the metal-deposited SPR optical fiber sensors with Au, Ag, Cu, and Al," Sensors and Actuators A: Physical, vol. 125, pp. 296-303, 2006.

[4]     E. Fontana, "Thickness optimization of metal films for the development of surface-plasmon-based sensors for nonabsorbing media," Applied optics, vol. 45, pp. 7632-7642, 2006.

[5]     T. Erdogan, "Cladding-mode resonances in short-and long-period fiber grating filters," JOSA A, vol. 14, pp. 1760-1773, 1997.

[6]     J. Thomas, N. Jovanovic, R. G. Becker, G. D. Marshall, M. J. Withford, A. Tünnermann, S. Nolte, M. Steel, "Cladding mode coupling in highly localized fiber Bragg gratings: modal properties and transmission spectra," Optics express, vol. 19, pp. 325-341, 2011.

[7]     J. Albert, L. Y. Shao, C. Caucheteur, "Tilted fiber Bragg grating sensors," Laser & Photonics Reviews, vol. 7, pp. 83-108, 2013.

[8]     L.-Y. Shao, J. P. Coyle, S. T. Barry, J. Albert, "Anomalous permittivity and plasmon resonances of copper nanoparticle conformal coatings on optical fibers," Optical Materials Express, vol. 1, pp. 128-137, 2011.

[9]     T. Allsop, R. Neal, S. Rehman, D. J. Webb, D. Mapps, I. Bennion, "Characterization of infrared surface plasmon resonances generated from a fiber-optical sensor utilizing tilted Bragg gratings," JOSA B, vol. 25, pp. 481-490, 2008.

[10]   G. Nemova, R. Kashyap, "Fiber-Bragg-grating-assisted surface plasmon-polariton sensor," Optics letters, vol. 31, pp. 2118-2120, 2006.

[11]   T. Allsop, R. Neal, S. Rehman, D. J. Webb, D. Mapps, I. Bennion, "Generation of infrared surface plasmon resonances with high refractive index sensitivity utilizing tilted fiber Bragg gratings," Applied optics, vol. 46, pp. 5456-5460, 2007.

[12]   J. Albert, S. Lepinay, C. Caucheteur, M. C. DeRosa, "High resolution grating-assisted surface plasmon resonance fiber optic aptasensor," Methods, vol. 63, pp. 239-254, 2013.

[13]   V. Voisin, C. Caucheteur, P. Mégret, J. Albert, "Interrogation technique for TFBG-SPR refractometers based on differential orthogonal light states," Applied optics, vol. 50, pp. 4257-4261, 2011.

[14]   L.-Y. Shao, Y. Shevchenko, J. Albert, "Intrinsic temperature sensitivity of tilted fiber Bragg grating based surface plasmon resonance sensors," Optics express, vol. 18, pp. 11464-11471, 2010.

[15]   Y. Y. Shevchenko, J. Albert, "Plasmon resonances in gold-coated tilted fiber Bragg gratings," Optics letters, vol. 32, pp. 211-213, 2007.

[16]   J. Zheng, X. Dong, J. Ji, H. Su, P. Ping Shum, "Power-referenced refractometer with tilted fiber Bragg grating cascaded by chirped grating," Optics Communications, vol. 312, pp. 106-109, 2014.

[17]   A. D. Rakic, A. B. Djurišic, J. M. Elazar, M. L. Majewski, "Optical properties of metallic films for vertical-cavity optoelectronic devices," Applied optics, vol. 37, pp. 5271-5283, 1998.