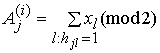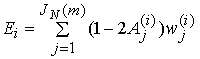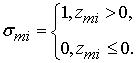УДК 621.391.01

ВЕРОЯТНОСТНЫЕ ХАРАКТЕРИСТИКИ ИТЕРАТИВНОГО ПРИЕМА ДИСКРЕТНЫХ СИГНАЛОВ НА ОСНОВЕ ПОМЕХОУСТОЙЧИВЫХ БЛОКОВЫХ НИЗКОПЛОТНОСТНЫХ КОДОВ

 

Л. Е. Назаров, М. А. Щеглов

Институт радиотехники и электроники им. В.А.Котельникова РАН, Фрязинский филиал

 

Статья получена 6 апреля 2015 г.

 

Аннотация. Приведены результаты сравнительного анализа характеристик алгоритмов итеративного приема дискретных сигналов, формируемых  на основе класса регулярных низкоплотностных кодов.

Ключевые слова: блоковые турбо-коды, низкоплотностные коды, алгоритмы итеративного приема, вероятность ошибки.

Abstract. This paper presents the symbol-by-symbol decoding algorithms for signal based on low-density parity-check codes and their error performances.

Key words: block product codes, low-density parity-check codes, iterative decoding.

 

Введение

Основные проблемы, решаемые при создании помехоустойчивых систем передачи дискретных сообщений различного назначения, связаны с разработкой эффективных алгоритмов обработки сигналов при их приеме [1].

В настоящее время интенсивно развивается теория ансамблей сигналов, для которых можно применить алгоритмы итеративного приема, т.е. представление оптимальной вычислительной процедуры посимвольного приема в виде более простой (подоптимальной) многоэтапной обработки реализаций с выхода сигнального демодулятора. Для широкого класса ансамблей сигналов этот подход приводит к существенному упрощению результирующей процедуры их приема при незначительной деградации вероятностных характеристик по отношению к вероятностным характеристикам оптимального приема [2,3,4].

Примерами ансамблей из данного класса являются сигналы на основе помехоустойчивых кодов под общим названием турбо-коды [2,5], а также сигналы на основе помехоустойчивых блоковых низкоплотностных кодов [6,7]. Исследования показывают, что эти ансамбли сигналов асимптотически оптимальны - при увеличении объемов информационных блоков (до тысячи битов и более) в совокупности с алгоритмами итеративного приема достигаются вероятностные характеристики, близкие к предельным характеристикам шенноновской пропускной способности каналов с аддитивным белым гауссовским шумом (АБГШ) [4,8].

В статье исследуются характеристики ряда алгоритмов итеративного приема дискретных сигналов, соответствующих классу низкоплотностных кодов на основе конечных геометрий (евклидово-геометрические коды, проективно-геометрические коды) [1,8], а также на основе форматного кода стандарта CCSDS [9], рекомендованного для использования в системах спутниковой связи. Основу исследуемых алгоритмов итеративного приема рассматриваемых сигналов составляет возможность организации системы одношаговых ортогональных соотношений относительно кодовых символов. Приведены оценки сложности реализации этих алгоритмов приема, определяемых объемом требуемых вычислительных операций и объемом требуемой памяти, а также их вероятностные характеристики, полученные путем компьютерного моделирования.

1. Постановка задачи

Рассматривается передача дискретных сообщений по каналу передачи без памяти с аддитивным белым гауссовским шумом с односторонней спектральной плотностью . Передача осуществляется с использованием дискретных сигналов с двоичной фазовой манипуляцией на основе двоичных блоковых кодов с параметрами () с проверочной матрицей  Здесь  - длительность кодовых слов ,  - размерность кода.

Пусть  - дискретная реализация с выхода демодулятора сигналов, поступающая на вход декодера, отсчеты реализации  задаются в виде , где  - сигнальные составляющие,  - помеховые составляющие, . Введем обозначение  - последовательность “жестких” решений, т.е.  при условии  и  в противном случае.

Полагается, что используемые блоковые коды обладают свойством организации множества ортогональных проверочных одношаговых соотношений для каждого кодового символа  кодовых слов  [1].

Пусть  - множество номеров позиций кодовых символов объемом , образующих -е проверочное соотношение;  - множество  без -го символа;  - множество проверочных ортогональных соотношений относительно кодового символа  объемом ;  - множество ортогональных проверок  без -ой проверки. Низкоплотностные коды, для которых выполняются условия  и  для всех , называются регулярными кодами.

Правило оптимального посимвольного приема сигналов  на основе обработки  заключается в вычислении апостериорных вероятностей для кодовых символов  [2]

.                                          (1)

Принятие решений относительно оценки  осуществляется по правилу: , если  и  в противном случае.

Объем арифметических операций, требуемый при вычислении (1), можно оценить соотношением , т.е. при увеличении размерности кода  реализация оптимального посимвольного приема представляет чрезмерно сложную проблему.

Альтернативу алгоритму оптимального посимвольного приема (1) относительно сложности технического исполнения составляют алгоритмы итеративного посимвольного приема [2].

Суть решаемой задачи - рассмотреть класс алгоритмов итеративного посимвольного приема ансамблей дискретных сигналов на основе низкоплотностных кодов со свойством одношаговой ортогонализации, произвести моделирование этих алгоритмов, дать сравнительный анализ их вероятностных характеристик и сложности реализации.

В статье рассмотрены наиболее эффективные алгоритмы итеративного посимвольного приема - алгоритм АРР (a’posteriori probability), алгоритм ВР (belief propagation) и их модификации [7,8].

2. Алгоритм итеративного приема АРР

При использовании алгоритма итеративного посимвольного приема АРР вычисляется оценка ошибки  () для кодовых символов  - оценка кодового символа  задается соотношением [8]:

.                                                                   (2)

Здесь  - сложение .

Алгоритм АРР, при реализации которого требуются арифметические операции «сложение-вычитание-сравнение», имеет следующие этапы обработки реализации  на каждой итерации [8].

Инициализация. Полагается . Вычисляется последовательность “жестких” решений: , если , и  в противном случае.

Вычисляются величины

.                                                    (3)

Шаг 1. Вычисляются величины

.                          (4)

Здесь параметр  определяет номер ортогональной проверки относительно кодового символа .

Шаг 2. На основе  вычисляются величины

.                                            (5)

Шаг 3. С использованием  вычисляются величины

.                                                                 (6)

Шаг 4. Если не выполняется условие на остановку работы алгоритма итеративного приема, то осуществляется последующая итерация, начиная с шага 1. В противном случае вычисляется оценка значения ошибки  на основе функции отношения правдоподобия

.                                            (7)

При условии  полагается , в противном случае . С использованием оценки  и соотношения (2) вычисляется результирующая оценка относительно кодового символа , .

Алгоритм итеративного приема АРР осуществляет параллельное использование величин  для вычисления , т.е. на шаге 2 вычисляется полное множество  и после этого реализуется шаг 3. Модификация этого алгоритма (m-APP) заключается в реализации последовательного использования величин  при вычислении , т.е. шаг 3 реализуется после вычисления очередного значения , , не требуя вычисления полного множества . В этом случае не требуется дополнительной памяти для хранения полного множества , что упрощает сложность технической реализации алгоритма m-APP по отношению к исходному алгоритму АРР.

При реализации итерации алгоритмов приема АРР и m-APP для дискретных сигналов на основе регулярных кодов объем требуемых вычислительных операций определяется вычислением выражений (4)-(6) и оценивается с использованием общего соотношения . При этом объем требуемой памяти равен  и .

3. Алгоритм итеративного приема ВР

Ниже приведены результирующие соотношения для алгоритма приема ВР, содержащего три этапа итеративной обработки  [7].

Инициализация. Устанавливаются начальные значения величин , .

Шаг 1. Вычисляется последовательность “жестких” решений

                                                       (8)

Для каждой ортогональной проверки  вычисляются величины

,                                              (9)

.                     (10)

Шаг 2. На основе значений  вычисляются величины  для последующей итерации

.                                             (11)

Шаг 3. При невыполнении условия реализации требуемого числа итераций выполняется шаг 1 последующей итерации, иначе принимается решение относительно передаваемых кодовых символов  с использованием величин

.                                                  (12)

Принимается решение , если , иначе .

Приведенный алгоритм итеративного приема ВР осуществляет параллельное использование величин  для вычисления значений  при реализации соотношения (11), т.е. на шаге 1 вычисляется полное множество  и после этого реализуется шаг 2. Модификация этого алгоритма (m-ВP) заключается в реализации последовательного использования величин  при вычислении , т.е. шаг 2 реализуется после вычисления очередного значения , , не требуя вычисления полного множества . В этом случае не требуется дополнительной памяти для хранения полного множества , что упрощает сложность технической реализации алгоритма m-ВP по отношению к исходному алгоритму ВР.

При реализации итерации алгоритмов приема ВР и m-ВP для дискретных сигналов на основе регулярных кодов объем требуемых вычислительных операций определяется вычислением выражений (8)-(11) и оценивается общим соотношением . При этом объем требуемой памяти равен  и .

4. Результаты моделирования алгоритмов итеративного приема

Для приведенных алгоритмов итеративного приема было произведено моделирование их работы для ряда низкоплотностных регулярных кодов с использованием модели АБГШ канала - для евклидово-геометрических кодов с параметрами (255,175) и (1023,781) [1]; для проективно-геометрического кода с параметрами (273,191) [1]; для кода с параметрами (8176,7156), входящего в состав форматных кодов CCSDS [9].

На рис.1 приведены вероятностные характеристики сигналов на основе проективно-геометрического низкоплотностного кода (273,191) с использованием алгоритма m-BP (кривая 1, 20 итераций) и с использованием алгоритма m-APP (кривая 2, 20 итераций). Параметры кода - , минимальное расстояние Хэмминга равно 17. Моделирование показало эквивалентность алгоритмов приема ВР и m-BP, а также АРР и m-APP для рассматриваемого низкоплотностного кода относительно вероятностных характеристик. По оси абсцисс отложены значения сигнал/помеха ,  - энергия на бит. Видно, что для вероятности ошибки на бит  энергетический выигрыш алгоритма m-BP по отношению к алгоритму m-APP составляет 0.3 дБ. Вместе с тем, при реализации алгоритма приема m-APP требуется в 2 раза меньше вычислительных операций и в 50 раз меньше требуемого объема памяти по отношению к алгоритму m-ВP.

Рис.1. Вероятностные характеристики ансамбля сигналов на основе
проективно-геометрического низкоплотностного кода (273,191):
1 - алгоритм итеративного приема m-BP (20 итераций);
2 - алгоритм итеративного приема m-APP (20 итераций).

На рис.2 приведены вероятностные характеристики сигналов на основе евклидово-геометрического низкоплотностного кода (255,175) с использованием алгоритма m-BP (кривая 1, 20 итераций) и с использованием алгоритма m-APP (кривая 2, 20 итераций). Параметры кода - , минимальное расстояние Хэмминга равно 16. В этом случае алгоритмы приема ВР и m-BP, а также алгоритмы АРР и m-APP эквивалентны относительно вероятностных характеристик. Видно, что для вероятности ошибки на бит  энергетический выигрыш алгоритма m-BP по отношению к алгоритму m-APP составляет 0.4 дБ. Вместе с тем, при реализации алгоритма приема m-APP требуется в 2 раза меньше вычислительных операций и в 48 раз меньше требуемого объема памяти по отношению к алгоритму m-ВP.

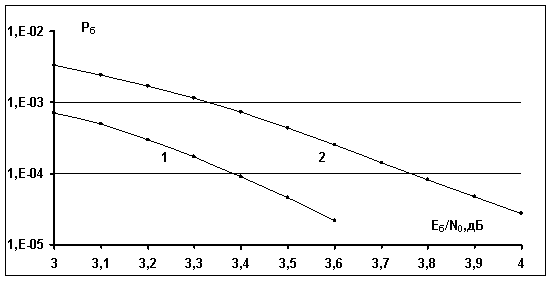
Рис.2. Вероятностные характеристики ансамбля сигналов на основе
евклидово-геометрического низкоплотностного кода (255,175):
1 - алгоритм итеративного приема m-BP (20 итераций);
2 - алгоритм итеративного приема m-APP (20 итераций).

На рис.3 приведены вероятностные характеристики сигналов на основе проективно-геометрического низкоплотностного кода (1023,781) с использованием алгоритма m-BP (кривая 1, 20 итераций) и с использованием алгоритма m-APP (кривая 2, 20 итераций). Параметры кода - , минимальное расстояние Хэмминга равно 32. В этом случае алгоритмы ВР и m-BP, а также алгоритмы АРР и m-APP эквивалентны относительно вероятностных характеристик. Видно, что для вероятности ошибки на бит  энергетический выигрыш алгоритма m-BP по отношению к алгоритму m-APP не превышает 0.5 дБ. При реализации алгоритма приема m-APP для этого кода требуется в 2 раза меньше вычислительных операций и в 95 раз меньше требуемого объема памяти по отношению к алгоритму m-ВP.

Рис.3. Вероятностные характеристики ансамбля сигналов на основе
проективно-геометрического низкоплотностного кода (1023,781):
1 - алгоритм итеративного приема m-BP (20 итераций);
2 - алгоритм итеративного приема m-APP (20 итераций).

 

Рис.4. Вероятностные характеристики ансамбля сигналов на основе
низкоплотностного кода (8176,7156) формата CCSDS:
1 - алгоритм m-ВР (10 итераций);
2 - алгоритм ВР (10 итераций);
3 - алгоритм m-АРP (10 итераций).

На рис.4 приведены вероятностные характеристики сигналов на основе низкоплотностного кода (8176,7156) формата CCSDS с использованием алгоритмов m-BP (кривая 1, 10 итераций), BP (кривая 2, 10 итераций) [8,10], m-APP (кривая 3, 10 итераций). Параметры кода -, , минимальное расстояние Хэмминга равно 32. Моделирование показало, что в этом случае алгоритмы АРР и m-APP эквивалентны относительно вероятностных характеристик. Вместе с тем, алгоритм m-BP является более эффективным алгоритма ВР - для вероятности ошибки на бит  энергетический выигрыш в этом случае достигает 0.1 дБ. Энергетический выигрыш алгоритма m-BP по отношению к алгоритму m-АРР для  достигает 1.6 дБ. При реализации алгоритма приема m-APP для этого кода требуется в 2 раза меньше вычислительных операций и в 8 раз меньше требуемого объема памяти по отношению к алгоритму m-ВP.

Заключение

Приведены описания алгоритмов итеративного посимвольного приема дискретных сигналов на основе низкоплотностных кодов со свойством организации одношаговых ортогональных проверочных соотношений для кодовых символов - алгоритмы APP, BP и их модификации m-APP и m-BP, более простые при реализации средствами цифровой вычислительной техники относительно требуемого объема памяти и объема вычислительных операций.

Путем моделирования для ряда регулярных низкоплотностных помехоустойчивых кодов на основе конечных геометрий (евклидово-геометрические и проективно-геометрические коды) показана эквивалентность вероятностных характеристик при их приеме с использованием алгоритмов m-APP и m-BP. Вместе с тем, при реализации алгоритма приема m-APP для этих кодов требуется в 2 раза меньше вычислительных операций и в 50-100 раз меньше объема памяти по отношению к реализации алгоритма m-ВP.

Моделирование алгоритмов приема для дискретных сигналов на основе низкоплотностного кода формата CCSDS (8176,7156) показало более высокую эффективность алгоритма m-BP по отношению к алгоритму ВР - для вероятности ошибки на бит  энергетический выигрыш достигает 0.1 дБ. При этом алгоритм m-АРР является существенно менее эффективным по отношению к алгоритму m-BP относительно их вероятностных характеристик.

 

Литература

1. Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. Перев. с англ. М.: Мир. 1976. 594 с.

2. Hagenauer J., Offer E., Papke L. Iterative decoding of binary block and convolutional codes. // IEEE Transactions on Information Theory. 1996. V. 42. N2. P.429-448.

3. Назаров Л.Е. Итеративный прием полосно-эффективных сигнально-кодовых конструкций, формируемых на основе турбо-кодов.// Радиотехника и электроника. 2004. Т.49. №11. Стр.1354-1361.

4 Назаров Л.Е., Головкин И.В. Класс турбо-кодов с пониженной сложностью алгоритмов декодирования. //Электросвязь. 2010. №7. Стр. 12-14.

5 Назаров Л.Е., Батанов В.В., Кузнецов О.О. Алгоритмы итеративного посимвольного приема блоковых турбо-кодов на основе кодов с проверкой на четность. // Журнал радиоэлектроники (электронный журнал). 2014. №9. http://jre.cplire.ru/jre/sep14/1/text.pdf.

6. Gallager R.G. Low-density parity-check codes.// IRE Transactions Information Theory. 1968. V.8. P.21-28.

7 MacKay D.J.C., Neal R.M. Near Shannon limit performance of low density parity check codes.// Electronics Letters. 1997. V,33. P.457-458.

8 Назаров Л.Е., Головкин И.В. Итеративный посимвольный прием ансамблей сигналов на основе низкоплотностных кодов. // Известия Вузов. Электроника. 2007. №3. Стр.43-49.

9. Research and Development for Space Data System Standards. Low density parity check codes for use in near-earth and deep space applications. Experimental specification CCSDS 131.1-O-2. September 2007.

10. Назаров Л.Е., Игошин Е.В., Зудилин А.С., Щеглов М.А. Разработка, реализация и испытания сигнально-кодовых конструкций для высокоскоростной радиолинии связи с БПЛА. // Успехи современной радиоэлектроники. 2014. №8. Стр. 68-7.