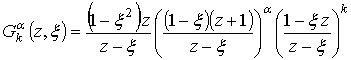УДК 681.518
УСЛОВИЕ ОПТИМАЛЬНОСТИ ФИЛЬТРОВ МЕЙКСНЕРА
С. А. Прохоров, И. М. Куликовских
Самарский
государственный аэрокосмический университет
им. академика С.П. Королева (национальный исследовательский университет)
Статья получена 8 апреля 2015 г.
Аннотация. В работе рассматриваются вопросы оптимизации фильтров Мейкснера, основанные на анализе необходимого и достаточного условий оптимальности для параметра масштаба. Для формирования фильтров Мейкснера выполнено модифицированное билинейное преобразование над обобщенными непрерывными фильтрами Лагерра. Результатами проведенных исследований являются теоретическое обоснование выбора условия оптимальности, построенное на вычислении коэффициентов связи между функциями Мейкснера, и серия вычислительных экспериментов для подтверждения теоретических результатов.
Ключевые слова: фильтры Мейкснера, модифицированное билинейное преобразование, коэффициенты связи, параметр масштаба, условие оптимальности.
Abstract. The paper delves into Meixner filters optimization problem based on considering necessary and sufficient conditions for scale parameter optimality. Applying modified bilinear transform to continuous generalized Laguerre filters, we introduced Meixner filters. The findings of this research present the convincing explanation for the optimality condition. We employed connection coefficients to work out relations for Meixner-like functions to provide this evidence and conducted a series of computational experiments to show the validity of the proposed results.
Key words: Meixner filters, modified bilinear transform, connection coefficients, scale parameter, optimality condition.
Введение
Одним из общепринятых подходов к оценке технического состояния сложной динамической системы является идентификация ее характеристик через обработку сигналов с целью определения структуры и параметров математической модели системы в базисе ортогональных функций [1-4]. Введение параметра масштаба для базисных функций позволяет значительно повысить качество данной модели при заданном числе членов разложения ортогонального ряда. Как результат, задача оптимизации процедуры идентификации систем при представлении их оператора рядом Лагерра рассматривалась многими авторами [4-12]. Работа [12] является одной из первых в данном направлении, в которой отмечается, что решением задачи оптимизации является одно из пары условий, определяемых приравниванием m-ого и (m+1)-ого коэффициентов ряда Фурье нулю. Тем не менее, в работе [5], а в последующем в [6-8], авторы указывают на целесообразность использования лишь (m+1)-ого коэффициента для определения оптимального значения параметра масштаба. В свою очередь, авторы [9, 10] пришли к аналогичному заключению относительно функций Лагерра, но указывают на неоднозначность выбора условия оптимальности в общем случае.
Сокращение количества условий снижает вычислительные затраты на решение задачи оптимизации параметров модели при обработке сигналов в два раза, так как при большом числе членов ряда возникает необходимость решения уравнений высокого порядка, в результате чего процедура оптимизации становится трудоемкой. Несмотря на значительное количество альтернативных менее ресурсозатратных, но квазиоптимальных алгоритмов поиска параметра масштаба, при решении ряда задач использование точного теоретического решения является критичным. Так в работе [13], автор указывает на необходимость использования именно оптимального алгоритма с использованием (m+1)-ого коэффициента разложения ряда Фурье для поиска значения параметра масштаба ввиду специфики предметной области [13-15], а именно, для улучшения отклика формирователя луча и получения выходного сигнала без искажений [13].
Как отмечалось ранее, в приведенных работах указывается целесообразность выбора одного из возможных условий в качестве критерия оптимальности, но не приводится ясных обоснований как для частного случая [5-9], так и для обобщенных функций Лагерра [10]. В работе [16] предлагается строгое математическое доказательство уникальности критерия оптимальности для непрерывных обобщенных функций и фильтров Лагерра, а также расширение полученных результатов на случай дискретных фильтров Лагерра. Однако отмечается, что рассмотрение обобщенных дискретных фильтров Лагерра [17, 18] – фильтров Мейкснера – находится за рамками исследования и требует доработки и расширения математического аппарата.
Таким образом, цель данной работы – определение условия оптимальности для фильтров Мейкснера, а также проведение серии экспериментов при решении практических задач обработки сигналов для подтверждения полученных результатов.
2. Фильтры Мейкснера
Пусть ![]() являются обобщенными
непрерывными ортогональными функциями Лагерра, полученными из ортогональных
полиномов для каждого фиксированного значения параметра масштаба
являются обобщенными
непрерывными ортогональными функциями Лагерра, полученными из ортогональных
полиномов для каждого фиксированного значения параметра масштаба ![]() , где
, где ![]() ,
, ![]() ,
, ![]() в
Гильбертовом пространстве
в
Гильбертовом пространстве ![]() . Для данной базисной
системы с весовой функцией
. Для данной базисной
системы с весовой функцией ![]() справедливо
справедливо
![]() ,
,
где ![]() – символ Кронекера,
– символ Кронекера, ![]() – норма функций.
– норма функций.
Представленная ортогональная система функций имеет рациональное преобразование Лапласа [16]
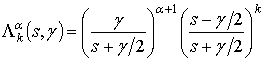 . (1)
. (1)
Для
формирования фильтров Мейкснера ![]() с действительным значением
параметра
с действительным значением
параметра ![]() необходимо применить модифицированное билинейное
преобразование [11] к выражению (1). Однако, так как мы имеем дело с
взвешенными ненормированными функциями, отличными от представленных в [10, 11],
представим пару билинейных преобразований в следующей форме
необходимо применить модифицированное билинейное
преобразование [11] к выражению (1). Однако, так как мы имеем дело с
взвешенными ненормированными функциями, отличными от представленных в [10, 11],
представим пару билинейных преобразований в следующей форме
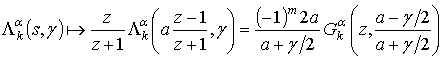 , (2)
, (2)
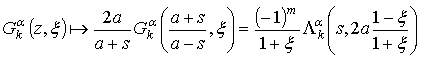 . (3)
. (3)
Применив (2) к (1), получим следующее рациональное z-преобразование, соответствующее обобщенным дискретным фильтрам Лагерра или фильтрам Мейкснера
Заметим, что
воспользовавшись (3) для решения обратной задачи, получим (1) из (4). Ряды
Мейкснера ![]() , соответствующие (4), также отличаются от
аналогичных функций, рассмотренных в [11, 17,
18], и имеют норму
, соответствующие (4), также отличаются от
аналогичных функций, рассмотренных в [11, 17,
18], и имеют норму ![]() . Важно также отметить, что полученные
фильтры (4) являются рациональными функциями в отличие от рассматриваемых ранее
[17, 18].
. Важно также отметить, что полученные
фильтры (4) являются рациональными функциями в отличие от рассматриваемых ранее
[17, 18].
3. Математическая постановка задачи
Функция ![]() , для которой
справедливо
, для которой
справедливо
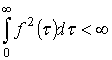
ожет быть представлена в форме ортогонального ряда с погрешностью
где ![]() – число членов ряда, коэффициенты
разложения
– число членов ряда, коэффициенты
разложения
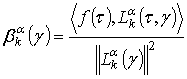 .
.
Пусть необходимо решить следующую задачу вида ![]() для каждого фиксированного
для каждого фиксированного ![]() и
и ![]() .
.
Тогда необходимо потребовать выполнения следующих условий
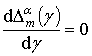 ,
, 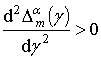 .
.
Найдя производную (5) и приравняв к нулю, можно записать
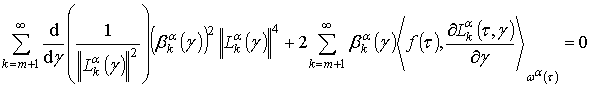 .
.
Тогда
коэффициенты связи ![]() [16, 19-21], следующие из
[16, 19-21], следующие из
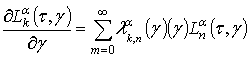 , где
, где
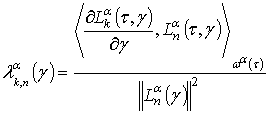 ,
,
после преобразований могут быть представлены в виде
Подставив (7) с учетом того, что ![]() для
диагоналей
для
диагоналей ![]() , смежных с главной, получим
, смежных с главной, получим
Исходя из того, что ![]() согласно
(7), нулевым является как минимум один из коэффициентов [4-13,
16]. Справедливость
условия
согласно
(7), нулевым является как минимум один из коэффициентов [4-13,
16]. Справедливость
условия ![]() для функций Лагерра
для функций Лагерра ![]() упоминается в работах [4-9,
11, 16], для
дискретных фильтров Лагерра
упоминается в работах [4-9,
11, 16], для
дискретных фильтров Лагерра ![]() – в работах [9,
11, 13],
и, наконец, содержит математическое обоснование для обобщенных функций Лагерра
– в работах [9,
11, 13],
и, наконец, содержит математическое обоснование для обобщенных функций Лагерра ![]() в работе [16]. Расширим полученные
результаты на случай обобщенных дискретных фильтров Мейкснера.
в работе [16]. Расширим полученные
результаты на случай обобщенных дискретных фильтров Мейкснера.
4. Условие оптимальности фильтров Мейкснера
Поставим задачу оптимизации фильтров Мейкснера ![]() по параметру
по параметру ![]() . Для этого зададим некоторую
передаточную функцию
. Для этого зададим некоторую
передаточную функцию ![]() , определенную на окружности с
радиусом больше 1 и меньше
, определенную на окружности с
радиусом больше 1 и меньше ![]() , которая может быть
представлена ограниченным ортогональным рядом со следующей погрешностью
приближения
, которая может быть
представлена ограниченным ортогональным рядом со следующей погрешностью
приближения
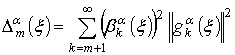 ,
, ![]() .
.
Тогда задача
оптимизации фильтров ![]() может быть представлена в виде
может быть представлена в виде
![]()
и требует выполнения необходимого и достаточного условий оптимальности, соответственно
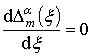 ,
,
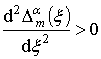 .
.
Необходимое условие оптимальности сводится к выражению, аналогичному (8). Представим достаточное условие в виде
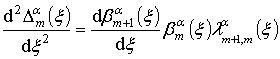 , (9)
, (9)
где ![]() – коэффициенты связи для фильтров
Мейкснера, полученные применением теоремы Парсеваля в z-плоскости к
– коэффициенты связи для фильтров
Мейкснера, полученные применением теоремы Парсеваля в z-плоскости к ![]() .
.
Оценим знак
(9) для каждого из случаев ![]() и
и ![]() .
.
Случай
1. Предположим,
что ![]() .
.
С учетом (7) и производной
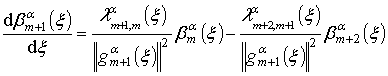
запишем (9) в виде
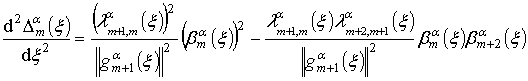 . (10)
. (10)
Исходя из
(10), принимая во внимание тот факт, что ![]() согласно
(7), можно сделать вывод, что
согласно
(7), можно сделать вывод, что
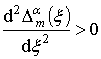 при условии
при условии ![]() . (11)
. (11)
Важно заметить, что для коэффициентов ![]() ,
выраженных через фильтры Мейкснера (4), справедливо следующее рекуррентное
соотношение.
,
выраженных через фильтры Мейкснера (4), справедливо следующее рекуррентное
соотношение.
![]() . (12)
. (12)
Соотношение (12) аналогично представленному в [16] для обобщенных непрерывных функций Лагерра, однако имеет противоположный знак.
С учетом допущения, что ![]() , из (12)
следует справедливость пары равенств
, из (12)
следует справедливость пары равенств
![]() ,
, ![]() . (13)
. (13)
Предположим,
что ![]() . Подставляя (13), а затем (12), получим
. Подставляя (13), а затем (12), получим
![]() ,
, ![]() ,
,
откуда
![]() . (14)
. (14)
Для справедливости (14), необходимо, чтобы выполнялось неравенство
![]() . (15)
. (15)
Применяя рекуррентное соотношение (11) к последнему
неравенству, получим ![]() , откуда с учетом неравенства
треугольника
, откуда с учетом неравенства
треугольника ![]() следует справедливость (15), а,
следовательно, и (14) и гипотезы (11). Таким образом, условие
следует справедливость (15), а,
следовательно, и (14) и гипотезы (11). Таким образом, условие ![]() решает задачу
решает задачу ![]() .
.
Случай
2. Предположим,
что ![]() .
.
Проведя ряд аналогичных преобразований, можно заключить
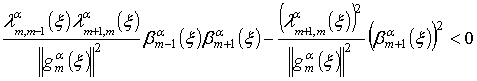 ,
,
что, в свою
очередь, свидетельствует о том, что ![]() решает задачу
решает задачу ![]() .
.
5. Экспериментальные исследования
С целью подтверждения теоретических результатов относительно справедливости выбранного условия оптимальности фильтров Мейкснера, проведем ряд вычислительных экспериментов. Зададим передаточную функцию впуска сверхзвукового реактивного двигателя [16, 22] в виде
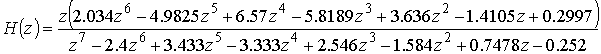 .
.
Необходимо решить задачу ![]() для
фиксированных
для
фиксированных ![]() и
и ![]() ,
рассчитав значения нормированных погрешностей
,
рассчитав значения нормированных погрешностей ![]() на
всем диапазоне
на
всем диапазоне ![]() . Решения уравнения
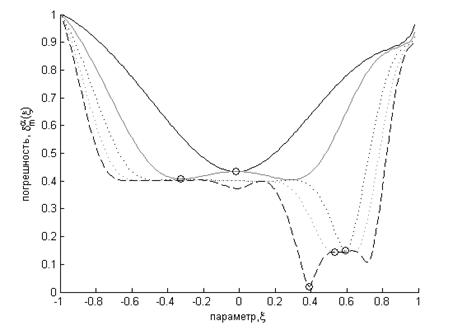
. Решения уравнения ![]() отмечены маркерами на рисунке 1, где в
качестве начального приближения выбрано значение
отмечены маркерами на рисунке 1, где в
качестве начального приближения выбрано значение ![]() = 0.48.
Численные значения результатов проведенных экспериментов представлены в таблице
1.
= 0.48.
Численные значения результатов проведенных экспериментов представлены в таблице
1.
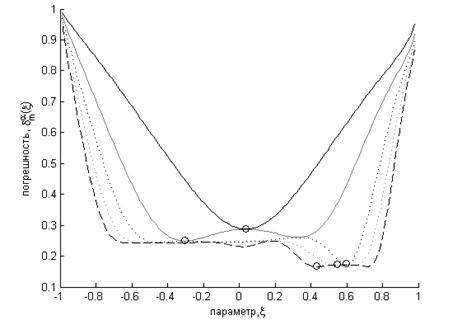
(a)
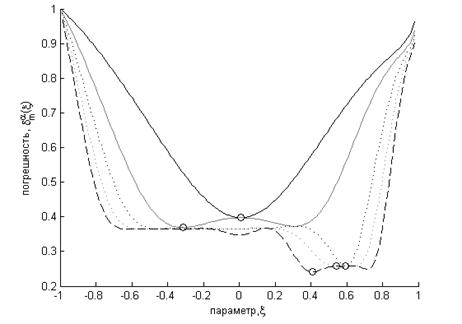
(b)
(c)
Рис. 1. Графические зависимости ![]() при изменении
при изменении ![]() :
:
(a) ![]() ; (b)
; (b) ![]() ; (c)
; (c) ![]()
Таблица 1. Численные значения результатов экспериментов
|
|
||||
|
m |
|
|
|
|
|
0 |
0.004 |
2.015 |
-0.348 |
|
|
1 |
-0.304 |
0.768 |
-0.106 |
|
|
2 |
0.597 |
0.826 |
-0.045 |
|
|
3 |
0.546 |
0.187 |
-0.089 |
|
|
4 |
0.433 |
0.247 |
-0.208 |
|
|
|
||||
|
m |
|
|
|
|
|
0 |
0.009 |
2.053 |
-0.333 |
|
|
1 |
-0.314 |
0.796 |
-0.105 |
|
|
2 |
0.594 |
0.828 |
-0.046 |
|
|
3 |
0.541 |
0.199 |
-0.099 |
|
|
4 |
0.409 |
0.336 |
-0.205 |
|
|
|
||||
|
m |
|
|
|
|
|
0 |
-0.016 |
2.098 |
-0.321 |
|
|
1 |
-0.032 |
0.826 |
-0.103 |
|
|
2 |
0.593 |
0.83 |
-0.052 |
|
|
3 |
0.531 |
0.238 |
-0.105 |
|
|
4 |
0.391 |
0.416 |
-0.194 |
|
Представленные на рисунке 1 графические зависимости с отмеченными
маркером значениями глобального минимума, являющегося решением уравнения ![]() , соответствуют
, соответствуют ![]() и
совпадают с
и
совпадают с ![]() , представленным в таблице 1. Совпадение
точек локальных максимумов и минимумов на всем диапазоне
, представленным в таблице 1. Совпадение
точек локальных максимумов и минимумов на всем диапазоне ![]() также свидетельствует о том, что условие
также свидетельствует о том, что условие ![]() решает альтернативную задачу
решает альтернативную задачу ![]() . В таблице также приведены значения
. В таблице также приведены значения ![]() и
и ![]() при
оптимальном
при
оптимальном ![]() для проверки справедливости неравенства
для проверки справедливости неравенства ![]() , положенного в основу теоретических
исследований. Как видно из представленных значений, данное неравенство является
справедливым для каждого
, положенного в основу теоретических
исследований. Как видно из представленных значений, данное неравенство является
справедливым для каждого ![]() и
и ![]() .
.
6. Выводы
Рассмотрена задача оптимизации фильтров Мейкснера ![]() по параметру
по параметру ![]() . В
результате проведенных теоретических исследований было получено и строго
обосновано, что лишь одно из пары возможных условий, а именно,
. В
результате проведенных теоретических исследований было получено и строго
обосновано, что лишь одно из пары возможных условий, а именно, ![]() является решением задачи
является решением задачи ![]() , обеспечивающей минимум-миниморум
погрешности приближения. В свою очередь, установлено, что
, обеспечивающей минимум-миниморум
погрешности приближения. В свою очередь, установлено, что ![]() дает решение
дает решение ![]() .
.
Для подтверждения теоретических результатов проведена серия
вычислительных экспериментов для передаточной функции впуска сверхзвукового
реактивного двигателя при ![]() и
и ![]() . Полученные результаты отметили целесообразность
проведенных исследований и адекватность найденного условия задачи оптимизации.
. Полученные результаты отметили целесообразность
проведенных исследований и адекватность найденного условия задачи оптимизации.
Практическим приложением предложенных в работе фильтров
Мейкснера ![]() является возможность представления
медленно возрастающих функций меньшим числом членов ряда
является возможность представления
медленно возрастающих функций меньшим числом членов ряда ![]() за счет использования параметра
за счет использования параметра ![]() в отличие от дискретных фильтров Лагерра,
а также применения в задачах синтеза фильтров, ввиду того, что
в отличие от дискретных фильтров Лагерра,
а также применения в задачах синтеза фильтров, ввиду того, что ![]() представляют собой рациональные функции.
представляют собой рациональные функции.
Финансирование
Работа выполнена при государственной поддержке Министерства образования и науки РФ в рамках реализации мероприятий Программы повышения конкурентоспособности СГАУ среди ведущих мировых научно-образовательных центров на 2013-2020 годы.
Литература
1. Л. В. Кузьмин, Р. Ю. Емельянов Система ортогональных сигналов для некогерентного приема сверхширокополосных хаотических радиоимпульсов в многолучевом канале. // Журнал радиоэлектроники: электронный журнал. 2014. №7. URL: http://jre.cplire.ru/iso/jul14/1/text.pdf
2. Д. А. Балакин, В. В. Штыков Построение ортогонального банка фильтров на основе преобразований Эрмита для обработки сигналов. // Журнал радиоэлектроники: электронный журнал. 2014. №8. URL: http://jre.cplire.ru/iso/sep14/1/text.pdf
3. В. Л. Петров Математическое обеспечение для идентификации электромеханической системы горных машин на основе представления оператора рядом функций Лагерра. // Горный информационно-аналитический бюллетень, 2002, №1, С. 330-334.
4. С. А. Прохоров Аппроксимативный анализ случайных процессов. – Самара: СНЦ РАН, 2001, – 380 с.
5. И. И. Волков, С. А. Прохоров Способ повышения точности аппроксимации корреляционных функций ортогональными функциями Лагерра. // Известия вузов СССР. Приборостроение, 1974, № 7(17), С. 66-72.
6. А. А. Бессонов, Ю. В. Загашвили, А. С. Маркелов Методы и средства идентификации динамических объектов. – Л.: Энергоатомиздат, 1989, – 280 с.
7. В. В. Филонников Выбор параметра модифицированных фильтров Лагерра при диагностировании линейной САУ. // Техническая диагностика, 2002, №2(4), С. 70-73.
8. А. Е. Нивин, А. В. Саушев, В. А. Шошмин Синтез ортогональных фильтров при статистической идентификации динамических систем. // Известия вузов. Приборостроение, 2013, № 10(56), С. 5-10.
9. T. Oliveira e Silva On the determination of the optimal pole position of Laguerre filters // IEEE Trans. Signal Process., 1995, vol. 40, pp. 2079-2087.
10. H. J. W. Belt, A. C. den Brinker Optimal parameterization of truncated generalized Laguerre series. // Proc. Int. Conf. on Acoustics, Speech, and Signal Processing (ICASSP), Munich, Germany, 21-24 April 1997, pp. 3805-3808.
11. H. J. W. Belt Orthogonal basis for adaptive filtering (Ph.D. thesis), Eindhoven University of Technology, May 1997.
12. G. Clowes Choice of the time-scaling factor for linear system approximations using orthonormal Laguerre functions. // IEEE Trans. Autom. Control, 1965, vol. 10, pp. 487-489.
13. S. R. Seydnejad, R. Ebrahimi Broadband beamforming using Laguerre filters. // Signal Processing, 2012, vol. 92, pp. 1093-1100.
14. K. M. alias Jeyanthi, A. P. Kabilan A simple adaptive beamforming algorithm with interference supression. // Журнал радиоэлектроники: электронный журнал. 2009. №6. URL: http://jre.cplire.ru/iso/jun09/1/text.pdf
15. А. А. Бабаскин, В. И. Калиничев Кольцевая антенная решетка для точек доступа с полным покрытием по азимуту. // Журнал радиоэлектроники: электронный журнал. 2014. №8. URL: http://jre.cplire.ru/iso/jun14/1/text.pdf
16. S. A. Prokhorov, I. M. Kulikovskikh Unique condition for generalized Laguerre functions to solve pole position problem. // Signal Processing, 2015, vol. 108, pp. 25-29.
17. A. C. den Brinker Meixner-like functions having a rational z-transform. // Int. J. Circuit Theory Appl., 1995, vol. 23, pp. 237-246.
18. C. J. Rivero-Moreno, S. Bres Temporal video indexing based on early vision using Laguerre filters. // Proc. Int. Conf. on Computer Analysis of Images and Patterns (CAIP), Versailles, France, 5-8 Sept. 2005, pp. 732-739.
19. R. Askey Orthogonal expansions with positive coefficients. // Proc. Amer. Math. Soc., 1965, №16, pp. 1191-1194.
20. W. F. Trench Nonnegative and alternating expansions of the one set of orthogonal polynomials in terms of another. // SIAM J. Math. Anal., 1973, vol. 4, pp. 111-115.
21. H. M. Ahmed Recurrence relations approach for expansion and connection coefficients in series of classical discrete orthogonal polynomials. // Integral Transforms and Special Functions, 2009, № 1(20), pp. 23-34.
22. M. Telescu, N. Iassamen, P. Cloastre, N. Tanguy A simple algorithm for stable order reduction of z-domain Laguerre models. // Signal Processing, 2013, vol. 93, pp. 332-337.