An interaction of a super strong linear-polarized electromagnetic wave with a dense plasma layer is investigated with the help of a self-consistent method of the analysis. It is shown that at falling a powerful harmonic wave at a thin plasma layer the reflected field can be in the form of ultrashort pulses of radiation with amplitude considerably larger than an amplitude of an incident wave. A process of interaction of a plasma layer with a standing electromagnetic wave is considered also and a generalization of classical results about character of an electron motion in an electromagnetic field is obtained for a case of a strong field and large radiation friction. In a strong field a minimum of an effective potential splits into two new that results in violation of a mirror symmetry of plasma layer radiation.

Keywords: Ultrashort pulse, plasma layer, laser-plasma interaction, radiation friction, radiation field

Recently large attention is given to the problems of generation of powerful ultrashort pulses and coherent electromagnetic radiation of high (up to x-ray) frequency through an interaction of a superstrong laser radiation with a solid target [1-6]. The reason for occurrence of high harmonics in a spectrum of reflected wave is the following: at falling a powerful electromagnetic wave with intensity on a target the electron plasma with large density (about the order of ) is formed on its boundary, the electrons of this plasma layer move not only in transversal direction but also commit the longitudinal vibrations at a double frequency under the action of magnetic component of the incident wave. There are two approaches now to the solution of such problems. First is based on a direct numerical simulation of Maxwell equations for process of interaction of plasma and powerful electromagnetic wave by a particle-in-cell method [2,4] and has all known lacks intrinsic to numerical experiments of such kind: technical complexity, difficulty of interpretation and selection of the physical solutions etc. In the second approach the simplified description permitting to receive analytical expressions is used. The model of an oscillating mirror is usually considered [1], in which the high harmonics in the reflected wave arise due to the periodic modulation of its phase: , where - is a frequency of an incident wave and is its initial phase. The incompleteness of such approach is due to the facts that, at first, the mirror is supposed to be absolutely reflecting, secondly, the time dispersion and dynamic relativistic effects are omitted. Besides the form of mirror oscillations in such approach is supposed to be harmonic that, generally speaking, does not correspond to the precise solution of self-consistent equations of motion for the plasma layer. At the same time at ultra relativistic amplitude of an external field when the work of a field on the wavelength becomes considerably larger than the rest energy of the electron (accelerating parameter ), the indicated effects should play an essential role. Actually at reflection of a wave from a mirror moving towards with constant speed the reflected amplitude is proportional to the factor, where is the ratio of mirror speed to the speed of light in vacuum [7]. In essentially relativistic regimes of interaction of the electromagnetic wave with the plasma layer (,) the form of the reflected field can evidently has a strong dependence on the amplitude factor .

The essential results describing the process of reflection of the powerful (ultra relativistic) electromagnetic wave from the plasma layer can be obtained within the framework of electron sheets model [8]. This model gives the consistent microscopic description of plasma layer interaction with electromagnetic waves and allows to solve many self-consistent problems about interaction of fields with charged medium. Especially simple equations of motion can be obtained in the case of small width of the plasma layer (considerably less than the wavelength of the incident radiation) when in the model it is possible to use one sheet only. Just this case will be considered in the present paper.

In particular it will be shown that at ultra relativistic amplitudes of the external field the reflected wave has essentially nonharmonic character: there is a synchronous radiation of harmonics of the incident wave frequency. Namely the sinusoidal incident wave can be converted into a sequence of short pulses of electromagnetic radiation with large amplitude. Thus due to the enrichment with the harmonics the decrease of each pulse duration takes place and the amplitude of pulses can essentially exceed the amplitude of the incident wave. The process of interaction of the plasma layer with a standing linear-polarized electromagnetic wave will be considered also and the generalization of the classical results about the character of electron motion in electromagnetic field [9] for the case of the strong field and large electron concentration (large radiation friction) will be obtained. It appears that in the strong electromagnetic field () each minimum of an effective potential splits into two new minima. It results in violation of a mirror symmetry of plasma layer radiation and dependence of the stationary state on the initial conditions due to essentially non-linear character of electron’s oscillations.

For simplicity in the following analysis we shall consider that an ion background is fixed and electron concentration in plasma is large enough, so that the frequency of an external field will be much less than plasma characteristic frequency. Besides we shall consider that the initial velocity of the electrons is zero (approximation of a cold plasma).

Let consider a charged medium homogeneous in directions perpendicular to Oz axis. In this case the densities of charge and current depend only on and are independent on and . Formal solutions of Maxwell equations can be in this case obtained by a method of a Green function and look like [8]:

(1)

Here [ , ] is the sign of a vector product.

Let now consider a thin layer of electrons extended in x and y-direction with the width considerably smaller than the wavelength of the incident radiation. In this case the layer is equivalent to an infinitely thin charged sheet the dynamics of which can be described by 3 + 1 functions of time: three components of speed and one space coordinate (fig.1).

Figure. 1. (3 + 1) - model of electron sheet.

The densities of charge and current of such sheet have the form:

,                                       (2)

where is the surface density of charge.

Substituting now expressions (2) in equations (1) and integrating over and , one can obtain the following expressions for the components of electromagnetic field:

,                                    (3)

where , , and the "delaying" time is determined from the equation .

It is worth to mention that the expressions (3) are one dimensional (or, more precisely, 3 + 1 dimensional) analogues of the classic Lienar-Wihert solutions [7] and give the exact expressions for the field created by the infinite plane. Here the component can be interpreted as a near field and component as a field of radiation.

Let consider an expression for a spectral component of the radiation field . Substituting into equation

                                                         (4)

the expressions for the field (1), one can receive

,                                     (5)

where and . Then using expression for the current density according to (2) one can obtain:

                                                       (6)

For periodic (with period ) motion of the plane the spectral decomposition of the radiation field contains only components at frequencies with values

.                                                   (7)

Let consider now an influence of the radiation field (3) on the motion of the electron sheet. It follows from expressions (3) that the interaction of the electron sheet with the own radiation field results in appearance of a specific self-action force [8]:

,                                           (8)

I.e. there is effective viscous force (8) with a constant coefficient of viscosity 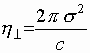for transversal motion and non-linear coefficient of viscosity 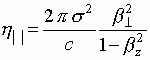for longitudinal motion.

The equations of motion for a separate electron of the sheet in homogeneous along x and y fields look like:

,

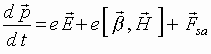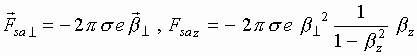                                                        (9)

Here is the relativistic momentum of the electron and is its charge.

Let at first consider a given longitudinal motion of the sheet. For transversal motion of the sheet in a field (normal falling of the linear-polarized wave at the plasma layer) one has from equations (9):

.                                 (10)

Let for simplicity the surface density of charge is large enough. In this case the sheet is practically an ideal mirror and, as was shown in Ref. [8], it is possible to neglect the inertial (dispersion) term in equation (10) (strictly speaking, the larger the greater should be the surface density for the sheet be the ideally reflecting mirror). Under these conditions the expression for the reflected wave has according to (3) the following form:

                                                   (11)

Note that the expression for the amplitude Doppler factor in this case appears valid not only for uniform motion but also for arbitrary dependence with replacement of t by the delaying time .

Let now the dependence of the longitudinal velocity on time is determined by an expression (a phase difference between the mirror oscillations and electromagnetic wave is determined by the value ). From (11) it follows that for the function A has a form of infinitely high pulses at the double frequency. The amplitude modulation of the reflected field due to the factor (cf. (11)) essentially enriches for the radiation spectrum so the shape of the reflected wave considerably differs from a sine wave. In fig. 2 the time dependence of the reflected field is displayed for different values of .

Figure. 2. Reflected field for (а) ; 0.9 (b); 0.99 (c).

There is a large number of odd harmonics of base frequency in the reflected wave and the closer is to unit the more harmonics is involved in the formation of the reflected wave. The principle point is the rigid binding for the phases of all harmonics to the phase of the incident wave. As a result all harmonics are added synchronously and the reflected field has the form of short pulses of radiation following with frequency with the amplitude directly proportional to the number of harmonics and with duration inversely proportional to that number. For relative complex amplitude of 2p + 1 harmonic one can obtain substituting the solution (11) into the spectral decomposition of the radiation field (7)

                 (12)

where the coefficients A and B are defined by the following expressions:

,

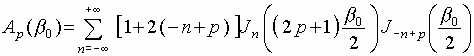
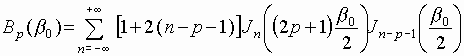Here is the Bessel function of the n-th order. Thus the expression (12) gives the precise analytical solution to the problem of reflection of the sine wave with frequency from the ideally reflecting mirror oscillating in the longitudinal direction with arbitrary amplitude and frequency . It is worth to mention that similar formulas can be obtained for the general case with dispersion.

The analysis of expression (12) gives not only a numerical value for a conversion coefficient of the incident wave power into harmonics, but also displays its strong dependence on the phase difference between the oscillations of the electron sheet and the wave.

Let proceed now to the self-consistent analysis of the reflected field in the case when the sheet moves under the action of the linear-polarized incident wave . Here contrary to the case considered in section 2 the dispersion of electron medium (inertial term) and highly nonharmonic character of electron oscillations will be taken into account. The trajectory of the electron sheet in this case can be presented as the sum of three components:

1). Transversal oscillations at the frequency of the incident wave.

2). Longitudinal oscillations at the double frequency of the incident wave.

3). Longitudinal drift under the action of a radiation pressure force.

At relativistic intensities the radiation pressure force acting on the sheet will be very large that will cause fast longitudinal acceleration of the sheet to about the speed of light; after that the sheet practically will stop to reflect the incident radiation. Therefore it is necessary to compensate the mean radiation pressure by, for example, an external electrostatic field (in real experiment such field can be produced by positive charge of heavy ions, for example. Actually for , where , the force of the electrostatic attraction from the ionic background appears to be larger than the force of light pressure, and the steady state regime is possible in the system). At for the full compensation of the radiation pressure force it is necessary to put [8]. In this case equations of motion (3) for the electron sheet have the following form:

                   (13)

where is a dimensionless compensatory force. A numerical analysis of the system (13) displays that the longitudinal oscillations of the electron sheet have essentially nonharmonic character for large that differs from the usually supposed sinusoidal law of motion. Besides there are parts of trajectory where the mirror moves towards to the incident wave with the speed close to the speed of light. According to expressions (3) just from these parts there is the radiation of large amplitude pulses (generation of high harmonics).

The most effective increase of reflected pulses’ amplitude and enrichment by harmonics occur according to (3) for the motion of the sheet towards the incident wave with the speed close to . For the oncoming acceleration of the electron sheet a swinging wave with frequency considerably smaller than the frequency of the incident radiation can be used in addition to the constant compensating field. Then the constant electrostatic field compensates the radiation pressure force of the incident wave and the swinging field provides at some moments the counter speed of the sheet close to the speed of light. Let, for example, the external field is selected in the form 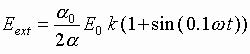, where the factor is introduced for the regime to be quasistationary. For this case the shape of the reflected field is shown in fig. 3 for and different values of and . The reflected field represents a set of trains following with frequency of the swinging wave ( in fig. 3) and each train consists of the short pulses with large amplitude which are radiated from the parts of trajectory where . The duration of each train is about the half of the swinging field period and there is a nonuniform effective compression of the train due to the Doppler conversion of the frequency. Distance between different trains in the set practically does not change because these segments correspond to the instants when and the Doppler frequency conversion is inessential. Note that here contrary to the approximation utilized in section 3 (fig. 2) accounting the inertial term results in the two-polar shape of each pulse.

Figure. 3. Radiation field of the plasma layer at the presence of the swinging field for (а) and (b).

It was already noted that the electron sheet commits finite oscillations in the field of the powerful electromagnetic wave when the radiation pressure force is compensated. In the previous section the force of radiation pressure was compensated by the homogeneous electrostatic field. However for the interaction of the electron sheet with the high-power electromagnetic wave the realization of such field in real experiment can be impossible. A more attractive scheme exists in which there are two waves of equal amplitudes running towards one another. Thus the problem of interaction of the electron sheet with a standing electromagnetic wave arises.

For electric and magnetic components of the standing linear-polarized wave one has:

; .                                              (14)

The equations of motion (9) will be recorded now in the following way:

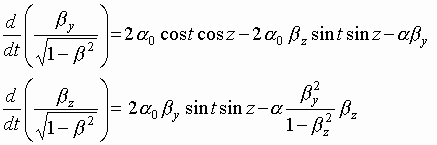.                                            (15)

The normalized dimensionless variables are introduced here.

Let at first . In this case equations (15) become:

.                                                    (16)

In the equation for the term should be taken into account despite of the smallness of longitudinal and transversal velocities of the electron sheet because the factor and this term can be about the order of remaining terms in the second equation of the system (16).

One can conclude that equations (16) belong to the well known type of particle’s equations of motion in a high frequency electromagnetic field when the force of the sheet self-action (radiation friction) described by the last term in (16) is neglected. The classical result [9] is that in the absence of radiation friction the longitudinal motion of particles represents fast oscillations at frequency and slow drift in an effective Gaponov-Miller potential (here character means time-averaging operation). It is natural to suppose that if there is a dissipation of energy due to the radiation the particles after some time will occur in a minimum of the potential energy ), i.e. in a node of the wave. At this points the electric field is equal to zero so the particles will stay at rest and will not radiate. Rigorous analysis of the system (16) displays that the inclusion of the non-linear radiation friction terms can essentially change the situation.

Let, for example, the condition is valid (this condition does not limit the analysis to a case of small amplitudes, since for any accelerating parameter it is possible to take rather large density for the sheet charge so that the condition remains valid). Retaining in equations (16) the terms of the first and second order in one can obtain for the slow longitudinal drift the following equation (see Appendix):

,                                            (17)

and for an effective potential energy and effective friction coefficient the expressions:

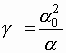,  .                                                             (18)

The first term in (18) corresponds to the Gaponov-Miller potential, the second one describes the effect of non-linear radiation friction. It can be shown that at the drift corresponds to the motion in the Gaponov-Miller potential: the steady state equilibrium position is in the node of the standing wave electric component (). However for the former equilibrium position becomes unstable, each effective potential minimum splits into two adjacent minima which for large tend to (fig. 4).

Figure. 4. Dependence of the normalized effective potential energy of the slow drift on longitudinal coordinate for different values of acceleration parameter: curve 1 - ; curve 2 - (point of bifurcation) and 3 -.

Comparing for an effective oscillation frequency near the minima of the potential energy with damping (cf. (18)) one can conclude that the drift of the sheet has a character of aperiodic motion to a new equilibrium position. At new equilibrium positions the amplitudes of electric and magnetic fields of the standing wave are nonzero so the electron sheet commits intensive oscillations at frequency in transverse direction and at frequency in longitudinal direction radiating the electromagnetic waves. Thus the effective radiation of the plasma layer in the field of standing wave is possible only for powerful enough fields ensuring (note that the analytical solution is obtained under condition of ). The numerical analysis for the complete set of equations of motion displays that taking into account the relativistic factors in the system (15) does not change qualitatively the character of the longitudinal drift. For large enough intensity of the standing wave the amplitude of the relativistic velocity of fast longitudinal anharmonic oscillations at frequency aims to unit and the radiation takes the form of a sequence of powerful pulses following at the double frequency of the wave. The shape of the radiation field is shown in the fig. 5 and 6. The essential point here is the dependence of the radiated field on the initial conditions. Actually if the initial value of the longitudinal coordinate is close to the equilibrium position then the steady-state amplitude of the radiation field is achieved practically during one-two periods of the incident wave. If initial position is far from equilibrium then at first one or two pulses are radiated with amplitude larger than the steady-state values (fig. 5) then a long period follows when the pulses have rather small amplitude and further the steady-state regime is achieved. Last case can be interesting to a problem of generation of ultra broadband single optical pulse.

Figure. 5. Non-stationary radiation field of the plasma layer in the transient regime: ; normalized initial coordinate of the layer .

Figure. 6. Radiation field of the plasma layer in positive (a) and negative (b) directions of axis for . The motion is near the left equilibrium position (with regard to the node of electrical component of standing wave).

Let mark another interesting effect arising due to a bifurcation in the considered system. For the radiation of the plasma layer acquires an asymmetrical character (fig. 6), i.e. fields radiated to the left and to the right are different. In this case not only the transient process of steady-state achievement but also the stationary state itself becomes dependent on the initial conditions. In fig. 7 the steady-state trajectories of an electron in the ultra relativistic case ( and ) are shown for some initial position of the layer.

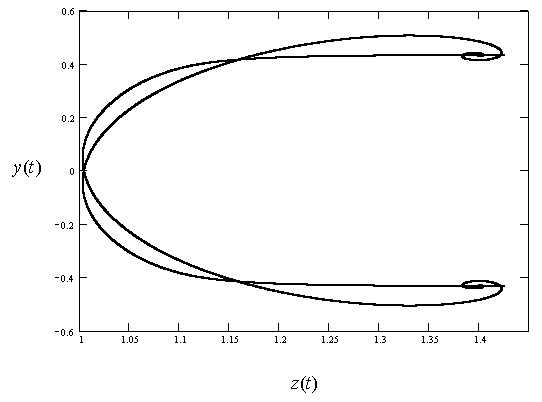
Figure. 7. Stationary trajectories of the plasma layer motion for (а) and 150 (b). The motion is near the left equilibrium position.

The asymmetry of the curves indicates asymmetry of radiation in the positive and negative directions of z axis. For other initial conditions the trajectory can be mirror reflected with regard to the node of electric component of the standing wave. The parameters of the layer radiation in this case change to the opposing.

Above considerations show that during interaction of the powerful electromagnetic wave with the dense plasma layer the sequence of ultrashort pulses with amplitude much greater than the amplitude of the incident wave can be generated.

Let estimate the value of acceleration parameter which can be realized experimentally now. From expression (8) one has for a power density of an incident radiation W/cm and a wavelength of 2 microns. The increase in the amplitude of the reflected pulses with regard to the amplitude of the incident wave is more than 15 times (see fig. 3a). Further advance in super-power laser pulses generation will allow to increase the acceleration parameter. For values (fig.3b) the intensity of the pumping wave about W/cm is necessary that does not seem inaccessible. An alternative way for the increase of efficiency of powerful ultrashort pulses generation during the reflection from the plasma layer can be the usage of cascaded reflection process that will be considered elsewhere.

Let estimate the value of parameter accessible in modern experiments. The surface density is determined by a volume concentration of electrons and by a thickness of the sheet. Let the wavelength of radiation falling at the sheet is . Then for the thickness of the sheet smaller than all points of the sheet will move practically along the same trajectories. For such case all expressions obtained for indefinitely thin sheet are valid (if the width of the medium is larger than then for the correct solution of the problem it is necessary to take into account the difference of velocities for different layers inside the sheet so the set of equations becomes more complicated though the proposed method is still usable). Thus for the electron concentration of the order of cm and the sheet width equal to one can obtain for parameter the value from 10 to 100 depending on the wavelength. It is obvious that for more thin sheets the value of can be made smaller.

In the present paper the perpendicular falling of the electromagnetic wave at the plasma sheet is considered. The obtained results can be easily generalized for the case of oblique falling using the method considered in Ref. [3]. Besides the proposed technique allows to find not only the reflected field but also the transmitted wave. For example in Ref. [8] the expression up to the third order in parameter is analytically retrieved for radiation passing through the thin plasma sheet.

For simplicity the ionic background was not considered in the above calculations. However one can easily take into account the effects of ions with the help of the approach used here for electrons. This is valid also if there is nontrivial initial distribution of electrons with velocity - for each value of velocity it is necessary to use the separate electron sheet with partial charge density, in this case the effective force of radiation reaction can be calculated by integrating over the velocity distribution function.

In experiment the thin plasma sheet model can be realized by evaporation of the freely suspended thin (about several microns or less) film by the powerful laser radiation. Probably this problem can be solved most naturally in the field of two counter propagating waves. It is necessary to note that the analogue of longitudinal low frequency swinging of the sheet considered in section 3 is evidently the case when one of the waves or both are modulated.

It is worth to mention in conclusion that the experimental confirmation of a capability of electromagnetic pulses’ generation can be obtained in interferometric experiments, for example, using the division of a wave front [11] already for a moderate value of incident radiation power. Also the optical nonlinearities can be used for demonstration in the scheme based on the effects of two-photon (multiphoton) luminescence [12,13].

In this appendix the analytical results concerning the character of the electron sheet motion in the field of two counter propagating waves used without proof in section 4 will be justified.

The equations (16) can be written as the system of three first order equations:

                                                  (A.1)

Let introduce the following dimensionless parameter (hereinafter we shall suppose that it is small): 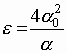. Then the equations (A.1) can be written in the following way:

                                               (A.2)

The solution of the first equation of a system (A.2) can be obtained with the method of sequential approximations, using for the transversal velocity the series expansion and equating factors with identical powers of . For the solution to within one has

       (A.3)

For the second bracket in the r.h.s. one can omit all terms proportional to and 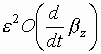. Substituting equation (A.3) into the system (A.2) one can obtain two equations of the first order:

                                  (A.4)

Introducing one has

.                                            (A.5)

The equations (A.5) can be solved by the averaging method [14,15], for what it is necessary to write them in a canonical form: . With this purpose we shall make a change of variables , where the function is choosen so that to compensate in the first equation of the system (A.5) the term . It is easy to test that for this purpose it is enough to put .

The system (A.5) in new variables has the form:

                (A.6)

Making now in (A.6) time-averaging operation one can obtain for the drift component of the longitudinal coordinate the following equation:

,                                             (A.7)

whence equation (17) directly follows. According to the averaging theorem [15] the error due to the replacement of the solutions of equations (A.6) by the solution of the average equation (A.7) have the order of evenly for the times of the order of .

1. D .Von der Linde, K. Rzazewski, “High-order optical harmonic generation from solid surfaces”, Appl. Phys. B., 63, pp. 499-506, 1996.
2. R. Lichters, J. Meyer-ter-Vehn, A. Pukhov, “Short-pulse laser harmonics from oscillating plasma surfaces driven at relativistic intensity”, Phys. Plasmas , 3, pp.3425-3437, 1996.
3. A. Bourdier, Phys. Fluids, 26, pp. 1804-1813, 1983.
4. P. Gibbon, “Harmonic generation by femtosecond laser-solid interaction: a coherent “water-window” light source?”, Phys. Rev. Lett., 76, pp. 50-53, 1996.
5. S. V. Bulanov, A. Macchi, F. Pegogaro, “On the theory of ionization of a thin foil by a laser pulse”, Phys. Lett. A., 245, pp. 439-444, 1998.
6. D. Bauer, R. R. E. Salomaa, P. Mulser, “Generation of ultrashort light pulses by a rapidly ionizing thin foil”, Phys. Rev. E, 58, pp. 2436-2440, 1998.
7. L. D. Landau, E. M. Lifshitz, Theory of the Field, Science, Moscow, 1967 (in russian).
8. A. S. Il’in, V. V. Kulagin, V. A. Cherepenin, “Radiation effects in the model of electron sheets”, J. of Comm. Tech. and Electronics, 44, pp. 389-400, 1999.
9. A. V. Gaponov, M. A. Miller, Sov. Phys. JETP, 34, pp. 242-251, 1958.
10. V. L. Bratman, S. V. Samsonov, “Radiation and radiative damping of a charged plane, oscillating with a relativistic velocity”, Phys. Lett. A, 206, pp. 377-382, 1995.
11. M. Born, E. Wolf, Principles of Optics, Pergamon Press, L-N.Y., 1968.
12. S. A. Akhmanov, Yu. E. Diakov, S. A. Chirkin, Introduction to Statistical Radiophysics and Optics, Science, Moscow, 1981 (in russian).
13. S. A. Akhmanov, V. A. Vysloukh, S. A. Chirkin, Optics of Femtosecond Laser Pulses, Science, Moscow, 1988 (in russian).
14. N. N. Bogolubov, Yu. A. Mitropolsky, Asymptotic methods in theory of non-linear oscillations, Science, Moscow, 1974 (in russian).
15. V. I. Arnold, Additional chapters of the theory of ordinary differential equations, Science, Moscow, 1978 (in russian).

Authors:
Anton S. Il'in, Victor V. Kulagin,  Vladimir A. Cherepenin and S.L. Ziglin