| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 7, 2001 |  |
ПРОСТРАНСТВЕННАЯ СЕЛЕКЦИЯ СИГНАЛОВ ПРОИЗВОЛЬНОЙ ПОЛЯРИЗАЦИИ
Д.
Д. Габриэльян, М. Ю. Звездина,
С. А. Черных
Ростовский военный институт ракетных
войск
Получена 18 апреля 2001 г.
Рассмотрены два алгоритма формирования весовых коэффициентов (адаптации) для подавления помеховых сигналов произвольной поляризации в антенной решетке с крестообразными электрическими вибраторами. Формирование общего весового множителя для сигналов, принятых обоими плечами, приводит к формированию "нулей" в обеих компонентах векторной диаграммы направленности независимо от вида поляризации помехового сигнала. Обеспечение независимого взвешенного суммирования указанных сигналов позволяет при линейной поляризации помехового сигнала формировать "нуль" только в одной из компонент диаграммы направленности. Приводятся результаты расчетов.
1. ВВЕДЕНИЕ
Пространственная селекция сигналов является одной из актуальных проблем современной антенной техники, т.к. позволяет максимизировать отношение сигнал/помеха+шум (ОСПШ) на выходе антенной решетки при одновременном приеме полезного и группы помеховых сигналов [1]. Несмотря на большое число работ, посвященных вопросам пространственной селекции сигналов, например [1-5], в них, как правило, рассматривается решение указанных вопросов применительно к антеннам с линейной поляризацией. В тоже время вопросы пространственно-поляризационной селекции сигналов для антенн круговой поляризации при воздействии на них полезного и группы помеховых сигналов произвольной поляризации не получили достаточного освещения. В связи с этим решение задач о нахождении амплитудно-фазового распределения, обеспечивающего максимальное ОСПШ для сигналов произвольной поляризации, является актуальной как в теоретическом плане так и с практической точки зрения.
В предлагаемой статье рассматривается решение задачи пространственно-поляризационной селекции сигналов на основе формирования "нулей" в одной или обеих компонентах векторной диаграммы направленности (ДН). Для простоты изложения будем рассматривать случай антенной решетки крестообразных вибраторов, расположенных в узлах прямоугольной сетки. Излучатели будем считать идентичными, а эффектами их взаимного влияния будем пренебрегать.
2. ЗАДАЧА ВЫБОРА АМПЛИТУДНО-ФАЗОВОГО РАСПРЕДЕЛЕНИЯ
Пусть
антенная решетка работает на одновременный прием K+1 сигналов. Каждый из
сигналов характеризуется направлением прихода
![]() и параметрами поляризационного эллипса
и параметрами поляризационного эллипса
![]() , причем индекс k=0
соответствует полезному сигналу, а индексы k из интервала
значений [1,K] – K помеховым сигналам. Угол
, причем индекс k=0
соответствует полезному сигналу, а индексы k из интервала
значений [1,K] – K помеховым сигналам. Угол
![]() отсчитывается от нормали к
плоскости раскрыва антенной решетки, угол
отсчитывается от нормали к
плоскости раскрыва антенной решетки, угол
![]() отсчитывается от положительного
направления оси 0x. Напряжение на выходе x- и y-плеч
n-го (n=1,¼, N)
излучателя, наводимое k-м сигналом, в соответствии с [6] может быть записано
в виде:
отсчитывается от положительного
направления оси 0x. Напряжение на выходе x- и y-плеч
n-го (n=1,¼, N)
излучателя, наводимое k-м сигналом, в соответствии с [6] может быть записано
в виде:
где
![]() ; i – мнимая
единица;
; i – мнимая
единица;
![]() ‑
координаты n-го излучателя в раскрыве антенной решетки;
‑
координаты n-го излучателя в раскрыве антенной решетки;
![]() ‑ диаграммы
направленности x- и y-плеча в направлении
‑ диаграммы
направленности x- и y-плеча в направлении
![]() соответственно;
соответственно;
![]() ‑ комплексная амплитуда
напряжения, соответствующая k-му сигналу.
‑ комплексная амплитуда
напряжения, соответствующая k-му сигналу.
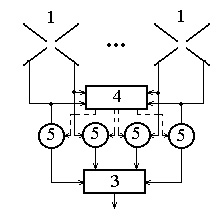
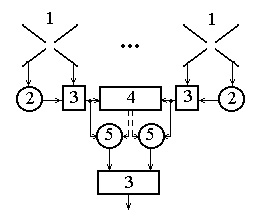
В работе [7] показана возможность независимого управления компонентами векторной ДН. В соответствии с этим возможны два варианта построения алгоритма формирования весовых коэффициентов: не учитывающий и учитывающий поляризационные параметры помеховых сигналов. Структурные схемы, соответствующие данным вариантам, приведены на рис.1, 2.
На
данных схемах использованы следующие обозначения: 1 – крестообразный
электрический вибратор; 2 – фазосдвигающий на
![]() элемент; 3 – сумматор; 4 – адаптивный
процессор; 5 – устройство, обеспечивающее комплексное взвешивание сигнала.
Сплошными линиями показаны линии передачи СВЧ-сигналов, штриховыми – линии
передачи сигналов управления с адаптивного процессора на устройство,
формирующее весовые коэффициенты.
элемент; 3 – сумматор; 4 – адаптивный
процессор; 5 – устройство, обеспечивающее комплексное взвешивание сигнала.
Сплошными линиями показаны линии передачи СВЧ-сигналов, штриховыми – линии
передачи сигналов управления с адаптивного процессора на устройство,
формирующее весовые коэффициенты.
При построении антенн по первому варианту сигнал на выходе n-го излучателя для k-го сигнала определяется формулой:
Мощности сигналов на выходе антенной системы могут быть записаны в виде
где
![]() ‑ N-мерный
вектор-столбец, элементами которого являются комплексные амплитуды весовых
коэффициентов в каналах антенны; т, * – символы операций транспонирования и
комплексного сопряжения;
‑ N-мерный
вектор-столбец, элементами которого являются комплексные амплитуды весовых
коэффициентов в каналах антенны; т, * – символы операций транспонирования и
комплексного сопряжения;
![]() ‑ матрица размерности N´N,
определяемая выражением
‑ матрица размерности N´N,
определяемая выражением
![]() .
.
Вектор
весовых коэффициентов
![]() ,
максимизирующий ОСПШ, определяется соотношением
,
максимизирующий ОСПШ, определяется соотношением
в котором
![]() ‑
мощность тепловых шумов в каналах антенной решетки; I
– единичная матрица размерности N´N.
‑
мощность тепловых шумов в каналах антенной решетки; I
– единичная матрица размерности N´N.
Для такой антенной системы x-компонента (x=q,j) диаграммы направленности может быть описана следующими равенством:
где
Анализ соотношений (6) показывает, что для алгоритма, построенного по первому варианту, формирование "нулей" будет происходить одновременно в обеих компонентах векторной ДН.
Для
независимого формирования "нулей" в каждой из компонент векторной ДН
необходимо осуществлять раздельное управление сигналами x-
и y-плеч каждого из излучателей. В этом случае вектор k-го
сигнала на выходе излучающих элементов представляет собой 2N-элементный
вектор-столбец, первые N элементов которого есть
![]() , а вторые N
элементов ‑
, а вторые N
элементов ‑
![]() . Мощность k-го
сигнала при использовании данного алгоритма формально определяется формулой
(3). Однако в данном случае вектор весовых коэффициентов имеет размерность 2N,
а матрица
. Мощность k-го
сигнала при использовании данного алгоритма формально определяется формулой
(3). Однако в данном случае вектор весовых коэффициентов имеет размерность 2N,
а матрица
![]() ‑
‑
![]() . При этом
выражение (4) сохраняет свою силу, но вектор
. При этом
выражение (4) сохраняет свою силу, но вектор
![]() имеет вид:
имеет вид:
![]() .
.
После данного переопределения вектора сигналов соотношение (5) сохраняет свою форму, хотя, как уже отмечалось, размерности входящих в него векторов и матриц удваиваются.
Компоненты векторной ДН при таком алгоритме управления весовыми коэффициентами определяются соотношениями (6), в которых
По найденным компонентам векторной ДН могут быть вычислены коэффициент направленного действия и отношение сигнал/помеха+шум. Последнее определяется выражением [2]
2. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ
Для
сравнения энергетических характеристик, обеспечиваемых с использованием
указанных алгоритмов, была рассмотрена антенная решетка 8´8 крестообразных электрических вибраторов с длиной
плеча
![]() ,
расположенных на высоте
,
расположенных на высоте
![]() над поверхностью бесконечной идеально
проводящей плоскости. Шаг размещения излучателей в составе раскрыва по обеим
координатам был выбран равным
над поверхностью бесконечной идеально
проводящей плоскости. Шаг размещения излучателей в составе раскрыва по обеим
координатам был выбран равным
![]() . Направленные свойства излучателей
определяются функциями
. Направленные свойства излучателей
определяются функциями
Из
представленных выше соотношений несложно заметить, что в случае помеховых
сигналов круговой поляризации использование обоих алгоритмов приводит к
одинаковым результатам. В связи с этим рассмотрим случаи линейно поляризованных
(![]() -поляризованных)
помеховых сигналов при работе адаптивной антенной решетки на прием сигналов
круговой поляризации.
-поляризованных)
помеховых сигналов при работе адаптивной антенной решетки на прием сигналов
круговой поляризации.
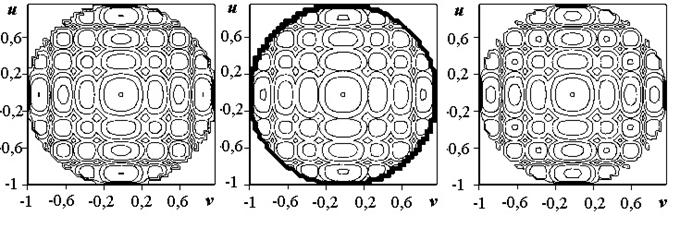
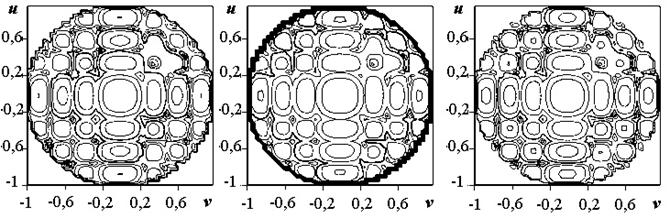
Карты
уровней диаграмм направленности в
обобщенной системе координат (![]() ,
,![]() ) при
использовании алгоритмов совместного и независимого управления токами в плечах
крестообразных вибраторов приведены на рис. 3-12. Во всех случаях рисунки с
индексом "а" соответствуют ДН по мощности, с индексом "б" ‑
) при
использовании алгоритмов совместного и независимого управления токами в плечах
крестообразных вибраторов приведены на рис. 3-12. Во всех случаях рисунки с
индексом "а" соответствуют ДН по мощности, с индексом "б" ‑
![]() -компоненте
ДН, с индексом "в" ‑
-компоненте
ДН, с индексом "в" ‑
![]() -компоненте. Мощности полезного и помехового
сигналов относительно мощности тепловых шумов антенной решетки составляли
-компоненте. Мощности полезного и помехового
сигналов относительно мощности тепловых шумов антенной решетки составляли
![]() и
и
![]() .
.
Для
удобства анализа на рис. 3 показана ДН, формируемая антенной решеткой в
отсутствие помех для неотклоненного луча (![]() ;
;
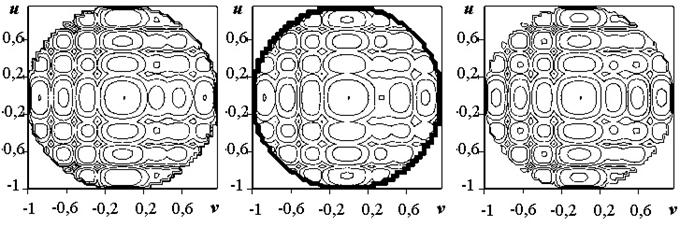
![]() ). Рис. 4, 5 иллюстрируют ДН в случае воздействия одного помехового
сигнала, приходящего с направления
). Рис. 4, 5 иллюстрируют ДН в случае воздействия одного помехового
сигнала, приходящего с направления
![]() (первый боковой лепесток в главном сечении
исходной ДН) и
(первый боковой лепесток в главном сечении
исходной ДН) и
![]() (первый
боковой лепесток в диагональном сечении) при применении первого алгоритма
управления (
(первый
боковой лепесток в диагональном сечении) при применении первого алгоритма
управления (![]() ). На рис. 6, 7 представлены ДН для аналогичных помеховых ситуаций при
использовании второго алгоритма управления (
). На рис. 6, 7 представлены ДН для аналогичных помеховых ситуаций при
использовании второго алгоритма управления (![]() ;
;
![]() ). Сравнение представленных результатов показывает, что применение
алгоритма с общим управлением "нули" ДН в направлениях прихода помеховых
сигналов формируются в обеих компонентах векторной ДН и, соответственно, в диаграмме
по мощности. Для второго алгоритма формирование "нулей" наблюдается
только в
). Сравнение представленных результатов показывает, что применение
алгоритма с общим управлением "нули" ДН в направлениях прихода помеховых
сигналов формируются в обеих компонентах векторной ДН и, соответственно, в диаграмме
по мощности. Для второго алгоритма формирование "нулей" наблюдается
только в
![]() -компоненте
векторной ДН рис.6б), а
-компоненте
векторной ДН рис.6б), а
![]() -компонента (рис.6в) остается без
изменений. Соответственно искажение диаграммы направленности по мощности
(рис.6а) значительно меньше, чем при использовании первого алгоритма (рис.3а).
Однако при попадании направления прихода помехового сигнала в диагональное
сечение (
-компонента (рис.6в) остается без
изменений. Соответственно искажение диаграммы направленности по мощности
(рис.6а) значительно меньше, чем при использовании первого алгоритма (рис.3а).
Однако при попадании направления прихода помехового сигнала в диагональное
сечение (![]() ) формирование
"нуля" ДН происходит в обеих компонентах векторной диаграммы
направленности. Это объясняется тем, что в данных сечениях вклад обоих плеч
излучателя в обе компоненты ДН одинаков.
) формирование
"нуля" ДН происходит в обеих компонентах векторной диаграммы
направленности. Это объясняется тем, что в данных сечениях вклад обоих плеч
излучателя в обе компоненты ДН одинаков.
Представляет
интерес возможность подавления линейно поляризованных сигналов, попадающих в
главный лепесток диаграммы направленности антенной решетки с излучателями
круговой поляризации. На рис. 8, 9 показаны результаты работы адаптивной
антенной решетки при использовании первого (рис.8) и второго (рис.9) алгоритмов
управления токами в плечах вибраторов. Полагалось, что помеха приходит с направления
![]() . Несложно
заметить, что применение алгоритма общего управления токами приводит к
разрушению (раздвоению) главного лепестка ДН в обеих компонентах векторной ДН
и, следовательно, в диаграмме направленности по мощности. Для второго алгоритма
данный эффект наблюдается только в
. Несложно
заметить, что применение алгоритма общего управления токами приводит к
разрушению (раздвоению) главного лепестка ДН в обеих компонентах векторной ДН
и, следовательно, в диаграмме направленности по мощности. Для второго алгоритма
данный эффект наблюдается только в
![]() -компоненте векторной ДН, что обуславливает
и значительно меньшие искажения в диаграмме направленности по мощности. Для
указанной помеховой обстановки снижение ОСПШ из-за действия помехи составляет 7
дБ для первого алгоритма и 4 дБ для второго алгоритма, а снижение коэффициента
направленного действия 1,5 дБ и 0,5 дБ соответственно.
-компоненте векторной ДН, что обуславливает
и значительно меньшие искажения в диаграмме направленности по мощности. Для
указанной помеховой обстановки снижение ОСПШ из-за действия помехи составляет 7
дБ для первого алгоритма и 4 дБ для второго алгоритма, а снижение коэффициента
направленного действия 1,5 дБ и 0,5 дБ соответственно.
Перейдем
к анализу вариантов с отклоненным главным лучом ДН. На рис.10 показана
диаграмма направленности, формируемая антенной решеткой при отклонении главного
лепестка в направлении
![]() ;
;
![]() в отсутствии помех. На рис. 11, 12 показаны карты уровней ДН при данном
положении главного максимума и направлении прихода помехи
в отсутствии помех. На рис. 11, 12 показаны карты уровней ДН при данном
положении главного максимума и направлении прихода помехи
![]() при использовании алгоритмов
общего и независимого управления токами в плечах крестообразного излучателя.
Как и в ранее рассмотренных случаях, реализация амплитудно-фазового распределения
на основе первого алгоритма формирование "нуля" наблюдается в обеих
компонентах векторной ДН и ДН по мощности. Для случая второго алгоритма
появление "нуля" отмечается только
при использовании алгоритмов
общего и независимого управления токами в плечах крестообразного излучателя.
Как и в ранее рассмотренных случаях, реализация амплитудно-фазового распределения
на основе первого алгоритма формирование "нуля" наблюдается в обеих
компонентах векторной ДН и ДН по мощности. Для случая второго алгоритма
появление "нуля" отмечается только
![]() -компоненте векторной ДН, а изменение
диаграммы направленности по мощности значительно меньше.
-компоненте векторной ДН, а изменение
диаграммы направленности по мощности значительно меньше.
3. ЗАКЛЮЧЕНИЕ
Анализ полученных результатов показывает, что при пространственной селекции помеховых сигналов круговой поляризации эффективность обоих рассматриваемых алгоритмов одинакова, однако при линейной поляризации помехи применение алгоритма с независимым формированием "нуля" в компонентах векторной диаграммы направленности обеспечивает лучшие энергетические характеристики. Наиболее эффективно применение предложенного алгоритма в случае подавления линейно поляризованных помеховых сигналов, попадающих в главный лепесток диаграммы направленности антенны с излучателями круговой поляризации.
|
Рис.1 |
Рис.2 |
а б в
Рис.3. Карта уровней компонентов ДН для помеховой
ситуации
![]()
а б в
Рис.4. Карта уровней компонентов ДН для помеховой ситуации
![]()
(общее управление токами в плечах излучателя)
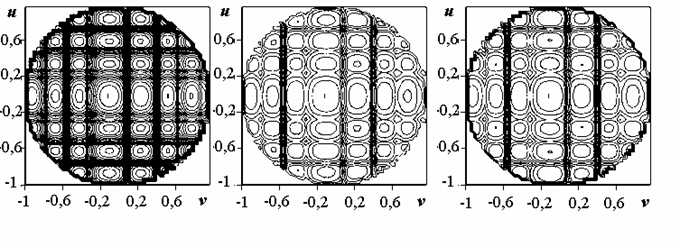
а б в
Рис.5. Карта уровней компонентов ДН для помеховой ситуации
![]()
(общее управление токами в плечах излучателя)
а б в
Рис.6. Карта уровней компонентов ДН для помеховой ситуации
![]()
(независимое управление токами в плечах излучателя)
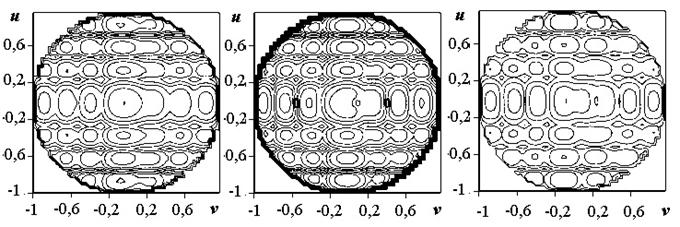
а б в
Рис.7. Карта уровней компонентов ДН для помеховой ситуации
![]()
(независимое управление токами в плечах излучателя)
а б в
Рис.8. Карта уровней компонентов ДН для помеховой ситуации
![]()
(общее управление токами в плечах излучателя)
а б в
Рис.9. Карта уровней компонентов ДН для помеховой ситуации
![]()
(независимое управление токами в плечах излучателя)
а б в
Рис.10. Карта уровней компонентов ДН для помеховой ситуации
![]()
а б в
Рис.11. Карта уровней компонентов ДН для помеховой ситуации
![]()
(общее управление токами в плечах излучателя)
а б в
Рис.12. Карта уровней компонентов ДН для помеховой ситуации
![]()
(независимое управление токами в плечах излучателя)
СПИСОК ЛИТЕРАТУРЫ
1. Проблемы антенной техники /Под ред. Л.Д. Бахраха, Д.И. Воскресенского. – М.: Радио и связь, 1989. – 368с.
2. Монзинго Р.А., Миллер Т.У. Адаптивные антенные решетки: Введение в теорию. – М.: Радио и связь, 1986. – 448 с.
3. Журавлев А.К., Лукошкин А.П., Поддубный С.С. Обработка сигналов в адаптивных антенных решетках. – Л.: Изд-во ЛГУ, 1983. – 240 с.
4. Лосев Ю.И., Бердников А.Г., Гойхман Э.Ш и др. Адаптивная компенсация помех в каналах связи. М.: Радио и связь, 1988. –207 с.
5. Нгуен Тан Динь, Нгуен Зи Линь. Свойства адаптивной антенной решетки управляемой поляризации при наличии группы полностью поляризованных помех // Изв. вуз. Радиоэлектроника. 1980. №9. С. 90-92.
6. Бахрах Л.Д., Кременецкий С.Д. Синтез излучающих систем (теория и методы расчета). – М.: Сов. радио, 1974. – 232 с.
7. Габриэльян Д.Д., Мануилов Б.Д., Мищенко С.Е., Сариев К.Э. Синтез векторной диаграммы направленности волноводной антенной решетки с многослойным диэлектрическим покрытием конечных размеров // Радиотехника и электроника. 2000. Т. 45. №3. С. 285-289.
Авторы:
ГАБРИЭЛЬЯН Дмитрий Давидович ‑ доктор технических наук, профессор РВИ РВ;
ЗВЕЗДИНА Марина Юрьевна ‑ кандидат технических наук, младший научный сотрудник РВИ РВ zvezd@jeo.ru;
ЧЕРНЫХ Сергей Александрович ‑ адъюнкт РВИ РВ.
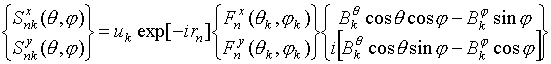 ,
(1)
,
(1)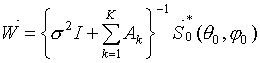 ,
(5)
,
(5)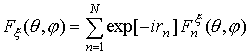 ,
,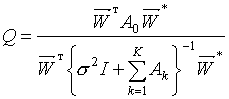 .
.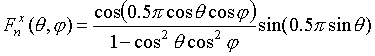 , (12)
, (12)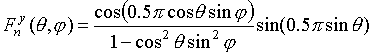 , (13)
, (13)