|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 8, 2002 |
|
МОДИФИЦИРОВАННЫЙ АЛГОРИТМ ВЫЧИСЛЕНИЯ КОЭФФИЦИЕНТОВ ВЗАИМНОЙ СВЯЗИ РАСПОЛОЖЕННЫХ ВБЛИЗИ КРУГОВОГО ЦИЛИНДРА ПРОДОЛЬНЫХ ЭЛЕКТРИЧЕСКИХ ВИБРАТОРОВ
Звездина М.Ю.; e-mail: zvezd@aaanet.ru
Ростовский военный институт ракетных войск
Получена 23 августа 2002 г.
В статье описывается модифицированный алгоритм вычисления коэффициентов взаимной связи системы продольных электрических вибраторов, расположенных вблизи импедансного кругового цилиндра. Отличие от традиционно используемого алгоритма заключается в аппроксимации распределения тока обобщенными модами и вычислении добавки, обусловленной особенностью спектрального представления функции Грина. Приводятся результаты вычислений величины добавки и коэффициентов связи для случаев размещения двух продольных вибраторов в свободном пространстве и вблизи импедансного кругового цилиндра.
Бурное развитие современных систем подвижной радиосвязи и телекоммуникаций, ведомственных и корпоративных спутниковых систем сделало актуальным задачу разработки антенн базовых станций. Одним из вариантов антенн, используемых в настоящее время для этих целей, является антенная решетка продольных вибраторов, расположенных вблизи импедансной цилиндрической несущей конструкции кругового сечения [1, 2]. Дальнейшее совершенствование антенн данного типа возможно только при проведении численных исследований на базе моделирования структуры возбуждаемого излучающим элементом электромагнитного поля. Точность получаемых при этом результатов во многом зависит от способа аппроксимации распределения тока в вибраторах. Так, в [3] показано, что при нахождении характеристик согласования, связанных с коэффициентами взаимной связи излучателей, достижение требуемой для практических целей точности результатов возможно только при аппроксимации распределения тока обобщенными модами.
Традиционный алгоритм вычисления
коэффициентов взаимной связи ![]() идентичных излучателей, расположенных
вблизи цилиндрической поверхности с произвольным импедансом, методом наводимых
ЭДС [4] описан в ряде работ, например, в [4-8]. В соответствии с ним структура
электромагнитного поля в ближней зоне моделируется в виде спектрального разложения
в интегралы Фурье, позволяющего представить функцию Грина в виде произведения
поперечной
идентичных излучателей, расположенных
вблизи цилиндрической поверхности с произвольным импедансом, методом наводимых
ЭДС [4] описан в ряде работ, например, в [4-8]. В соответствии с ним структура
электромагнитного поля в ближней зоне моделируется в виде спектрального разложения
в интегралы Фурье, позволяющего представить функцию Грина в виде произведения
поперечной ![]() и
продольной
и
продольной ![]() составляющих
[5-11]:
составляющих
[5-11]:
где ![]() для всех видов сечений
цилиндрического тела;
для всех видов сечений
цилиндрического тела; ![]() ‑ продольное волновое число;
‑ продольное волновое число;![]() ‑
поперечное волновое число, связанное в предположении о малых потерях в импедансной
среде с продольным волновым числом
‑
поперечное волновое число, связанное в предположении о малых потерях в импедансной
среде с продольным волновым числом ![]() и волновым числом свободного пространства
и волновым числом свободного пространства ![]() соотношением
соотношением ![]() ;
; ![]() ‑ длина
волны;
‑ длина
волны; ![]() ‑
мнимая единица;
‑
мнимая единица; ![]() ,
, ![]() ‑ координаты радиус-векторов
соответственно точки наблюдения и точки интегрирования в цилиндрической системе
координат
‑ координаты радиус-векторов
соответственно точки наблюдения и точки интегрирования в цилиндрической системе
координат ![]() .
.
С использованием данного представления поля nm-й
элемент матрицы коэффициентов взаимной связи 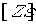 , описывающий связь n-го
продольного вибратора с m-м (
, описывающий связь n-го
продольного вибратора с m-м (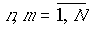 ) продольным вибратором, определяется
соотношением [4,5]:
) продольным вибратором, определяется
соотношением [4,5]:

 ,
,
где ![]() ‑ длина плеча вибратора;
‑ длина плеча вибратора; ![]() ;
; ![]() ‑
амплитуды токов в точке питания n-го и m-го излучателей;
‑
амплитуды токов в точке питания n-го и m-го излучателей; ![]() ‑ функции, описывающие распределение
тока в вибраторах;
‑ функции, описывающие распределение
тока в вибраторах; ![]() ‑ вычеты подынтегрального выражения,
взятые в полюсах функции
‑ вычеты подынтегрального выражения,
взятые в полюсах функции ![]() ; L – контур
интегрирования. Вид контура интегрирования и нахождение вычетов подробно
описаны в работах [7, 8] и здесь не рассматриваются.
; L – контур
интегрирования. Вид контура интегрирования и нахождение вычетов подробно
описаны в работах [7, 8] и здесь не рассматриваются.
При аппроксимации распределения
тока ![]() в
в
![]() -м
вибраторе обобщенными модами
-м
вибраторе обобщенными модами
 ,
,
nm-й
элемент матрицы коэффициентов взаимной связи из (2) после выполнения преобразований
данного выражения по известному алгоритму (см., например, [4,5,7]) становится
блочным, имеющим размерность ![]() (
(![]() ‑ число мод тока, используемых для
аппроксимации распределения тока в вибраторе), и приобретает вид:
‑ число мод тока, используемых для
аппроксимации распределения тока в вибраторе), и приобретает вид:
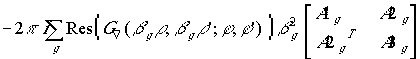 .
.
В выражениях (3), (4) ![]() ‑
координаты центра
‑
координаты центра ![]() -го излучателя;
-го излучателя; ![]() ‑ дельта-функция
Дирака;
‑ дельта-функция
Дирака; ![]() ‑
неизвестные комплексные амплитуды токов, определяемые из условия равенства нулю
тангенциальных составляющих электрического поля на поверхности электрического
вибратора;
‑
неизвестные комплексные амплитуды токов, определяемые из условия равенства нулю
тангенциальных составляющих электрического поля на поверхности электрического
вибратора; ![]() ‑
символ транспонирования;
‑
символ транспонирования; ![]() ‑ блочные матрицы размерностью
‑ блочные матрицы размерностью ![]() , описывающие
связь
, описывающие
связь ![]() -го
и
-го
и ![]() -го
вибраторов на
-го
вибраторов на ![]() -х (
-х (![]() ) модах для косинусных, смешанных и синусных
гармоник соответственно. Индексом «
) модах для косинусных, смешанных и синусных
гармоник соответственно. Индексом «![]() » обозначена дискретная составляющая,
обусловленная
» обозначена дискретная составляющая,
обусловленная ![]() -м полюсом функции
-м полюсом функции ![]() .
.
Соотношения, полученные в
соответствии с данным алгоритмом для вычисления коэффициентов взаимной связи
расположенных вблизи импедансного кругового цилиндра продольных электрических
вибраторов, ток в которых описывается различными законами, известны и
приводятся в ряде работ, например, в [7,8,12]. Однако в случае аппроксимации
распределения тока с использованием обобщенных мод данный алгоритм имеет
ограничение. В частности, при нахождении реактивных составляющих собственных коэффициентов
связи на одинаковых модах тока (![]() ) при численном интегрировании возникают
расходящиеся слагаемые, соответствующие особенности функции Грина при расположении
точки источника и точки наблюдения в одной плоскости [9].
) при численном интегрировании возникают
расходящиеся слагаемые, соответствующие особенности функции Грина при расположении
точки источника и точки наблюдения в одной плоскости [9].
Цель данной статьи – разработка численного алгоритма, позволяющего выделить особенность функции Грина и исключить расходящиеся слагаемые при нахождении коэффициентов взаимной связи расположенных вблизи кругового импедансного цилиндра продольных электрических вибраторов, ток в которых аппроксимируется обобщенными модами.
Анализ выражений (2) и (4)
показывает, что появление расходящихся слагаемых в данных соотношениях вызван
особенностью интегрального ядра 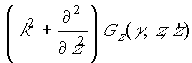 при
при ![]() и
и ![]() . Выделение данной особенности будем
проводить по стандартному алгоритму, описанному, например, в [9], начиная с понижения
порядка производной. С этой целью выполним интегрирование выражения
. Выделение данной особенности будем
проводить по стандартному алгоритму, описанному, например, в [9], начиная с понижения
порядка производной. С этой целью выполним интегрирование выражения
по частям, учитывая при этом
симметричность продольной компоненты спектральной составляющей функции Грина ![]() относительно
аргументов
относительно
аргументов ![]() и
и
![]() , а
также условие обращение в нуль тока на концах тонкого вибратора [4]. После
выполнения интегрирования по частям выражение (5) может быть записано в виде
суммы однократного
, а
также условие обращение в нуль тока на концах тонкого вибратора [4]. После
выполнения интегрирования по частям выражение (5) может быть записано в виде
суммы однократного ![]() и двукратного
и двукратного ![]() интегралов, определяемых соотношениями:
интегралов, определяемых соотношениями:
Используя аппроксимацию (3)
для распределения тока, интегралы ![]() для элементов блоков
для элементов блоков ![]() могут быть записаны в
виде:
могут быть записаны в
виде:
где
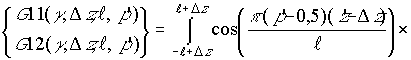

Анализ
соотношений (11)-(14) показывает, что возникновение особенностей функции Грина
возможно в случаях, когда вибраторы хотя бы частично перекрываются (![]() ). На
рис.1,а
показан случай частичного перекрытия вибраторов (
). На
рис.1,а
показан случай частичного перекрытия вибраторов (![]() ), а на рис.1,б –
расположения излучателей на расстоянии
), а на рис.1,б –
расположения излучателей на расстоянии ![]() . Штриховкой на указанных рисунках показано
возможное расположение зон, в которых возникает особенность функции Грина. Несложно
заметить, что расположение и размер зон (
. Штриховкой на указанных рисунках показано
возможное расположение зон, в которых возникает особенность функции Грина. Несложно
заметить, что расположение и размер зон (![]() или
или ![]() ) зависит как от кратности интеграла, так и
от степени перекрытия вибраторов.
) зависит как от кратности интеграла, так и
от степени перекрытия вибраторов.
Представим интегралы (11)-(14) в
виде суммы интегралов двух типов: не содержащих и содержащих особенность функции
Грина и допускающих различную точность при проведении расчетов. Для этого
выделим из областей интегрирования зоны, в которых возникает особенность
функции Грина. При этом предположим, что размер данных зон не превышает ![]() , где
, где ![]() ‑
некоторая фиксированная малая величина.
‑
некоторая фиксированная малая величина.
В замкнутой форме выражения для
двукратных интегралов ![]() , не содержащих особенность функции Грина,
имеют вид:
, не содержащих особенность функции Грина,
имеют вид:
при ![]() и
и
при ![]() ;
;
Аналитические соотношения для однократных интегралов из соотношений (13), (14), из которых выделена особенность функции Грина, имеют вид:
При ![]() сумма
сумма ![]() совпадает с
соответствующими выражениями, полученными для двукратных интегралов. При
частичном перекрытии вибраторов переменная
совпадает с
соответствующими выражениями, полученными для двукратных интегралов. При
частичном перекрытии вибраторов переменная ![]() при
при ![]() описывается теми же выражениями,
что и для двукратных интегралов, а переменная
описывается теми же выражениями,
что и для двукратных интегралов, а переменная ![]() имеет вид:
имеет вид:
для интегралов
![]() :
:
для
интеграла ![]() :
:
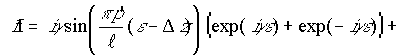
При ![]() переменные
переменные ![]() и
и ![]() описываются
соотношениями:
описываются
соотношениями:
Интегралы, содержащие
особенность функции Грина, как отмечалось ранее, отличны от нуля только при ![]() и также могут
быть записаны в свернутой форме:
и также могут
быть записаны в свернутой форме:
где
а однократные интегралы
где
С использованием
приведенных соотношений традиционный алгоритм вычисления коэффициентов взаимной
связи расположенных вблизи кругового импедансного цилиндра продольных
излучателей, ток в которых аппроксимирован обобщенными модами, может быть
модифицирован следующим образом. Вычисления проводятся в два этапа. На первом
этапе для всех ![]() излучателей вычисляются интегралы (15),
(26). При этом верхняя граница второго интервала, на который разбивается контур
интегрирования
излучателей вычисляются интегралы (15),
(26). При этом верхняя граница второго интервала, на который разбивается контур
интегрирования ![]() , может быть небольшой. Затем только для
вибраторов, расположенных на расстоянии
, может быть небольшой. Затем только для
вибраторов, расположенных на расстоянии ![]() , с использованием выражений (31), (33)
вычисляется добавка, обусловленная особенностью функции Грина. Верхняя граница
второго интервала интегрирования должна быть высокой, обеспечивающей требуемую
точность вычисления.
, с использованием выражений (31), (33)
вычисляется добавка, обусловленная особенностью функции Грина. Верхняя граница
второго интервала интегрирования должна быть высокой, обеспечивающей требуемую
точность вычисления.
Определим размеры зоны, в
которой будет вычисляться особенность функции Грина. Для используемого
представления поля зададим зону особенности функции Грина в виде цилиндра
длиной ![]() и
радиусом
и
радиусом ![]() ,
причем
,
причем
Для тонких вибраторов
параметр ![]() ,
как показано в [3,4], имеет величину порядка
,
как показано в [3,4], имеет величину порядка ![]() . Отношение
. Отношение ![]() длины зоны особенности
к его радиусу должно составлять целую величину из интервала чисел
длины зоны особенности
к его радиусу должно составлять целую величину из интервала чисел ![]() . В большинстве
случаев достаточно принять
. В большинстве
случаев достаточно принять ![]() .
.
3. РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ИССЛЕДОВАНИЙ
С использованием
приведенных выше соотношений в языковой среде MathCad 7.0 Pro
был разработан пакет программ, позволяющий проводить вычисления матрицы
коэффициентов решетки продольных электрических вибраторов, расположенных как в
свободном пространстве, так и вблизи кругового цилиндра радиуса ![]() , поверхностный
импеданс которого описывается тензором
, поверхностный
импеданс которого описывается тензором 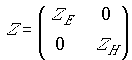 , где
, где ![]() ‑ волновые сопротивления в
классах
‑ волновые сопротивления в
классах ![]() и
и
![]() волн
соответственно.
волн
соответственно.
В случае размещения излучателей в свободном пространстве в качестве поперечной функции Грина использовалась функция, описываемая соотношением [10]:
а при размещении вибраторов вблизи импедансного кругового цилиндра – функцией, определяемой выражением [7, 8]:
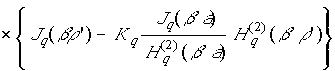 ,
,
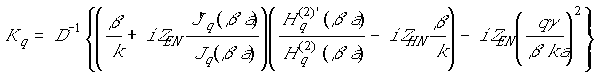 ;
;
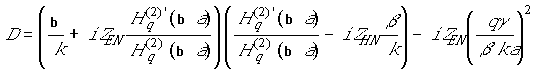 ;
;
где ![]() ‑ функция Бесселя q-го порядка и ее производная;
‑ функция Бесселя q-го порядка и ее производная; ![]() ‑ функция
Ганкеля q-го порядка 2-го рода и ее производная
соответственно;
‑ функция
Ганкеля q-го порядка 2-го рода и ее производная
соответственно; ![]() ;
; ![]() ;
; ![]() Ом;
Ом; ![]() ‑ амплитуда тока в точке пучности.
‑ амплитуда тока в точке пучности.
В табл. 1 приводятся
результаты вычислений добавки в собственные и взаимные коэффициенты связи на ![]() -х обобщенных
модах (
-х обобщенных
модах (![]() )
двух продольных вибраторов с длиной плеча
)
двух продольных вибраторов с длиной плеча ![]() при размещении излучателей в
свободном пространстве и на удалении
при размещении излучателей в
свободном пространстве и на удалении ![]() от поверхности кругового цилиндра радиусом
от поверхности кругового цилиндра радиусом
![]() для
трех значений величины поверхностного импеданса: нулевого и двух анизотропных с
для
трех значений величины поверхностного импеданса: нулевого и двух анизотропных с
![]() и
и ![]() . Для оценки
величины добавки в табл.2 приведены окончательные значения коэффициентов связи,
для которых проводились расчеты. При составлении табл.1 и
табл.2 учтена
симметричность матрицы коэффициентов взаимной связи относительно главной
диагонали, а также исключены элементы, равные нулю.
. Для оценки
величины добавки в табл.2 приведены окончательные значения коэффициентов связи,
для которых проводились расчеты. При составлении табл.1 и
табл.2 учтена
симметричность матрицы коэффициентов взаимной связи относительно главной
диагонали, а также исключены элементы, равные нулю.
Расчеты проводились при разных значениях верхних границ отрезков интегрирования. Так, при вычислении интегралов, не содержащих особенность функции Грина, данная величина принималась равной 30 для случая размещения в свободном пространстве и 13 – при расположении излучателей вблизи кругового цилиндра. Вычисление добавки проводилось при верхней границе, равной соответственно 2000 и 100. Время вычислений каждого варианта под управлением операционной системы Win2K на ЭВМ с процессором AthlonXP-1700+ и оперативной памятью 256 Мб составило порядка 10 мин.
Анализ данных из
табл.1 и
табл.2 показывает, что в случае аппроксимации распределения тока в продольных
вибраторах с использованием обобщенных мод при вычислении собственных
коэффициентов связи величина добавки, обусловленной особенностью функции Грина,
велика, особенно для реактивной составляющей, и отлична от нуля только для
диагональных элементов в блоках одинаковых гармоник (![]() ). Для элементов,
расположенных на расстоянии
). Для элементов,
расположенных на расстоянии ![]() , добавка присутствует во всех элементах
блоков, однако ее вклад в соответствующий коэффициент связи значительно меньше.
Для элементов, удаленных на большие расстояния, добавка равна нулю, поскольку
особенности функции Грина при этом не возникает.
, добавка присутствует во всех элементах
блоков, однако ее вклад в соответствующий коэффициент связи значительно меньше.
Для элементов, удаленных на большие расстояния, добавка равна нулю, поскольку
особенности функции Грина при этом не возникает.
Сравнение данных табл.2 с аналогичными, но полученными с использованием других алгоритмов [3,5], позволяет сделать вывод о корректности разработанных программ и достаточной для практических целей точности получаемых результатов. Анализ временных затрат показал, что в случае расположения вибраторов в свободном пространстве вычисления все же целесообразнее проводить с использованием функции Грина свободного пространства. При размещении излучателей вблизи цилиндра временные затраты сопоставимы с данным параметром для известных алгоритмов.
Таким образом, при
аппроксимации распределения тока с использованием обобщенных мод при вычислении
коэффициентов взаимной связи расположенных вблизи импедансного кругового
цилиндра продольных вибраторов для излучателей, смещенных вдоль оси ![]() на расстояния,
меньшие двух длин плеч вибратора, необходимо вычислять добавку, обусловленную
особенностью функции Грина.
на расстояния,
меньшие двух длин плеч вибратора, необходимо вычислять добавку, обусловленную
особенностью функции Грина.
Величина добавки в коэффициент связи на ![]() -х модах тока,
-х модах тока,
обусловленной особенностью функции Грина
|
№ в блоке ( |
Свободное пространство |
Круговой цилиндр |
||
|
|
|
|
||
|
|
||||
|
Блок |
||||
|
(2,2) |
-58,6-1,73·103i |
-59,2-1,429·103i |
-80,7-1,426·103i |
-84,2-1,418·103i |
|
(3,3) |
-173,1-5,139·103i |
-174,8-4,246·103i |
-238,2-4,237·103i |
-248,6-4,214·103i |
|
Блок |
||||
|
(1,1) |
-22,11-650,78i |
-22,3-537,7i |
-30,4-536,5i |
-31,8-533,5i |
|
(2,2) |
-109,17-3,23·103i |
-110,3-2,669·103i |
-150,3-2,663·103i |
-156,8-2,648·103i |
|
(3,3) |
-249,5-7,443·103i |
-251,9-6,151·103i |
-343,4-6,137·103i |
-358,4-6,103·103i |
|
|
||||
|
Блок |
||||
|
(1,1) |
0,09+1,93i |
0,09+1,57i |
0,13+1,56i |
0,13+1,55i |
|
(1,2) |
-0,28-5,79i |
-0,28-4,7i |
-0,38-4,69i |
-0,39-4,65i |
|
(1,3) |
0,46+9,64i |
0,47+7,84i |
0,64+7,81i |
0,66+7,75i |
|
(2,2) |
0,83+17,29i |
0,84+14,06i |
1,14+14,02i |
1,19+13,91i |
|
(2,3) |
-1,38-28,83i |
-1,39-23,44i |
-1,9-23,36i |
-1,98-23,18i |
|
(3,3) |
2,28+47,74i |
2,31+38,82i |
3,14+38,68i |
3,28+38,79i |
|
Блок |
||||
|
(1,1) |
-0,19-3,86i |
-0,19-3,14i |
-0,25-3,13i |
-0,27-3,1i |
|
(1,2) |
0,37+7,71i |
0,37+6,27i |
0,51+6,25i |
0,53+6,2i |
|
(1,3) |
-0,56-11,57i |
-0,56-9,41i |
-0,76-9,38i |
-0,79-9,3i |
|
(2,2) |
-1,11-23,07i |
-1,12-18,75i |
-1,52-18,69i |
-1,59-18,54i |
|
(2,3) |
1,66+34,59i |
1,67+28,13i |
2,28+28,03i |
2,38+27,81i |
|
(3,3) |
-2,74-57,29i |
-2,77-46,58i |
-3,77-46,32i |
-3,93-46,06i |
|
Блок |
||||
|
(1,1) |
-0,37-7,7i |
-0,37-6,26i |
-0,51-6,24i |
-0,53-6,19i |
|
(1,2) |
0,74+15,41i |
0,74+12,53i |
1,02+12,49i |
1,06+12,39i |
|
(1,3) |
-1,11-23,11i |
-1,12-18,79i |
-1,52-18,73i |
-1,59-18,58i |
|
(2,2) |
-1,47-30,67i |
-1,48-24,94i |
-2,02-24,85i |
-2,11-24,65i |
|
(2,3) |
2,2+46,0i |
2,23+37,4i |
3,03+37,27i |
3,16+36,98i |
|
(3,3) |
-3,27-68,46i |
-3,3-55,65i |
-4,49-35,46i |
-4,69-55,02i |
Коэффициенты связи на ![]() -х модах тока
-х модах тока
|
№ в блоке ( |
Свободное пространство |
Круговой цилиндр |
||
|
|
|
|
||
|
|
||||
|
Блок |
||||
|
(1,1) |
73,13+41,79i |
86,18+64,23i |
100,01+32,28i |
101,61+19,41i |
|
(1,2) |
-20,3-85,06i |
-24,8-77,18i |
-27,92-73,01i |
-27,96-69,08i |
|
(1,3) |
12,06+86,56i |
14,76+67,6i |
16,59+65,12i |
16,61+62,73i |
|
(2,2) |
5,937-2,291·103i |
7,39-1,812·103i |
8,19-1,833·103i |
8,15-1,832·103i |
|
(2,3) |
-3,53-176,87i |
-4,4-111,25i |
-4,88-110,54i |
-4,85-109,61i |
|
(3,3) |
2,11-5,857·103i |
2,62-4,538·103i |
2,91-4,559·103i |
2,89-4,556·103i |
|
Блок |
||||
|
(1,1) |
8,61-911,9i |
8,27-747,74i |
11,44-767,25i |
12,49-767,23i |
|
(1,2) |
-3,96-136,15i |
-3,86-106,07i |
-5,27-106,14i |
-5,73-105,14i |
|
(1,3) |
2,6+144,69i |
2,54+101,59i |
3,46+101,65i |
3,76+100,98i |
|
(2,2) |
1,83-3,832·103i |
1,8-3,07·103i |
2,43-3,09·103i |
2,63-3,087·103i |
|
(2,3) |
-1,2-218,33i |
-1,19-134,3i |
-1,59-134,36i |
-1,73-133,99i |
|
(3,3) |
0,8-7,764·103i |
0,78-6,144·103i |
1,05-6,16·103i |
1,13-6,16·103i |
|
|
||||
|
Блок |
||||
|
(1,1) |
26,41+19,73i |
36,6+24,49i |
37,82+15,89i |
34,91+10,5i |
|
(1,2) |
-9,97-40,7i |
-13,51-38,56i |
-14,12-36,31i |
-13,51-34,35i |
|
(1,3) |
6+42,14i |
8,11+36,33i |
8,49+34,98i |
8,13+33,78i |
|
(2,2) |
3,41+74,02i |
4,52+61,01i |
4,81+60,25i |
4,65+59,43i |
|
(2,3) |
-2,06-87,7i |
-2,72-66,96i |
-2,89-66,51i |
-2,81-66i |
|
(3,3) |
1,23+11,74i |
1,62+79,76i |
1,73+79,49i |
1,67+79,18i |
|
Блок |
||||
|
(1,1) |
-16,18-43,19i |
-17,61-46,05i |
-21,61-42,98i |
-22,67-40,05i |
|
(1,2) |
3,93+61,5i |
4,26+52,28i |
5,02+51,65i |
5,18+50,66i |
|
(1,3) |
-2,31-66,90i |
-2,26-49,97i |
-2,62-49,61i |
-2,69-49,03i |
|
(2,2) |
-1,87-82,38i |
-2,12-65,27i |
-2,52-64,94i |
-2,59-64,4i |
|
(2,3) |
0,93+97,85i |
1,09+71,77i |
1,25+71,59i |
1,28+71,28i |
|
(3,3) |
-0,73-120,08i |
-0,83-83,77i |
-0,98-83,64i |
-1,01-83,43i |
|
Блок |
||||
|
(1,1) |
-2,5-60i |
-1,38-54,68i |
-3,24-56,01i |
-4,02-55,71i |
|
(1,2) |
1,06+68,43i |
0,57+56,66i |
1,36+57,18i |
1,70+56,95i |
|
(1,3) |
-0,7-72,45i |
-0,38-56,16i |
-0,9-56,5i |
-1,13-56,34i |
|
(2,2) |
-0,44-93,72i |
-0,22-71,06i |
-0,57-71,27i |
-0,71-71,12i |
|
(2,3) |
0,31+108,23i |
0,17+77,44i |
0,39+77,58i |
0,49+77,47i |
|
(3,3) |
-0,18-130,19i |
-0,09-88,69i |
-0,236-88,79i |
-0,29-88,72i |
- Климашов И.А. Антенны для базовых станций сотовой связи// Технологии и средства связи. 2002. №2. С.40-45.
- Николаев В.П. Позиционирование подвижных объектов в сетях сотовой связи // Технологии и средства связи. 2002. №2. С.50-58.
- Овсянников В.В. Вибраторные антенн с реактивными нагрузками, – М.: Радио и связь, 1985. – 120 с.
- Антенны УКВ / Под ред. Г.З. Айзенберга в 2-х ч.Ч.1. – М.: Радио и связь, 1977. – 384 с.
- Кравцов В.А., Кравцова Г.В. Взаимные сопротивления продольных вибраторов, расположенных вблизи кругового цилиндра // Радиотехника. 1978. Т.33 № 2. С.85-90.
- Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. – М.: Радио и связь, 1983. – 296 с.
- Звездина М.Ю. Вычисление взаимной связи крестообразных вибраторов в присутствии импедансного кругового цилиндра // Журнал радиоэлектроники. 2002. №2. http:/jre.cplire.ru/feb02/3/text.html.
- Габриэльян Д.Д., Звездина М.Ю., Костенко П.И. Возбуждение кругового цилиндра с анизотропным импедансом продольным электрическим диполем // Радиотехника и электроника. 2001. Т.46. №8. С.875-879.
- Фелсен Л., Маркувиц Н. Излучение и рассеяние волн. Т.1 Т.2. – М.: Мир, 1978, – 548 с., 556 с.
- Каценеленбаум Б.З. Высокочастотная электродинамика. – М.: Наука, 1966. – 240 с.
- Шевченко В.В. Плавные переходы в открытых волноводах. – М.: Наука, 1969. – 192 с.
- Габриэльян Д.Д., Звездина М.Ю. Взаимное сопротивление продольных вибраторов вблизи импедансного кругового цилиндра // Радиотехника. 2000. №5. С.67-69.
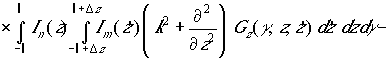 (2)
(2)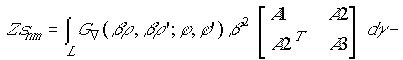 (4)
(4) (5)
(5)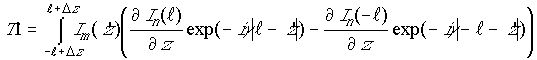 , (6)
, (6)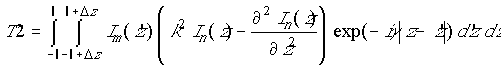 . (7)
. (7)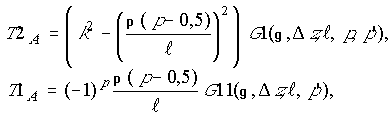 (8)
(8)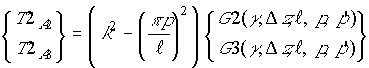 ,
(9)
,
(9) ,
(10)
,
(10) ; (11)
; (11) ;
(12)
;
(12)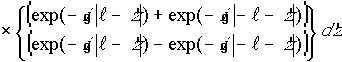 ; (13)
; (13)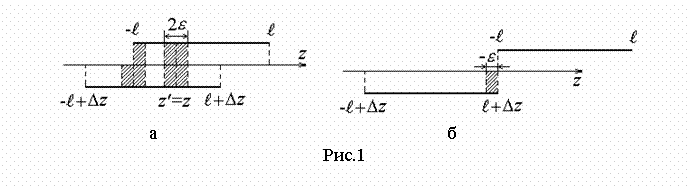
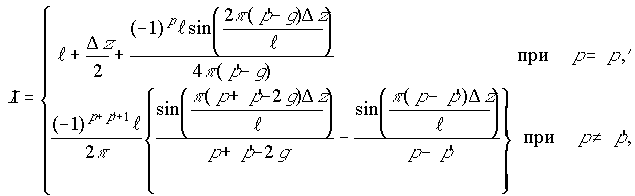
 , (15)
, (15)
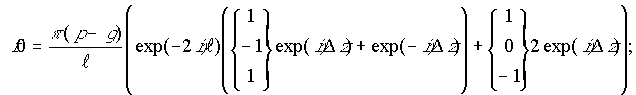
 ;
; 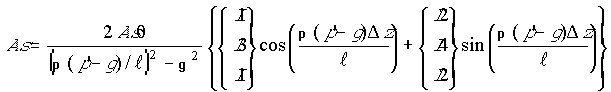 ;(20)
;(20) ;
(21)
;
(21) (22)
(22)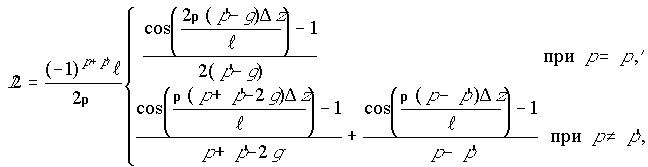 (23)
(23)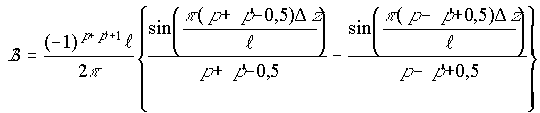 ;
(24)
;
(24)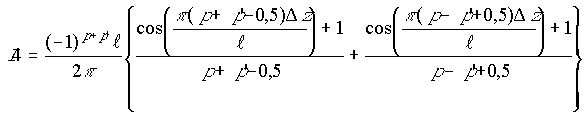 . (25)
. (25) .
(26)
.
(26)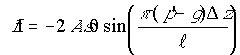 (27)
(27)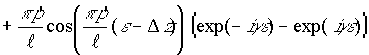 .
(28)
.
(28)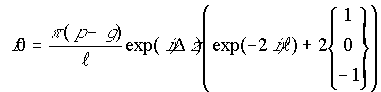 ;
(29)
;
(29)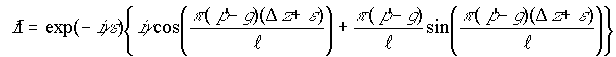 . (30)
. (30)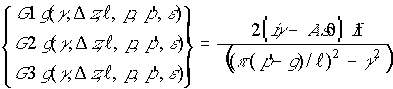 ,
(31)
,
(31) ;
(32)
;
(32)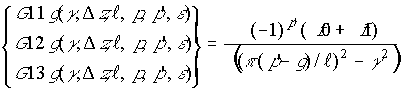 ,
(33)
,
(33) (34)
(34) (35)
(35)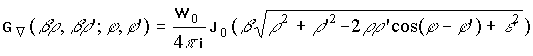 , (37)
, (37)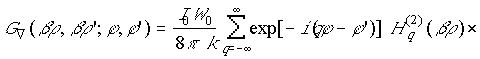 (38)
(38)