Квантово-энергетические и кинетические свойства материалов кремниевой наноэлектроники на основе кластеров Si2-Si10

УДК 537.311.322

квантово-энергетические и кинетические свойства материалов кремниевой наноэлектроники на основе кластеров Si₂-Si₁₀ А. Н. Власов, В. В. Филиппов
Липецкий государственный педагогический университет, кафедра физики

Получена 27 июня 2011 г., после доработки – 22 августа 2011 г.

Аннотация. Выполнен анализ квантовохимических методов расчета структурных, энергетических и транспортных параметров кремниевых наночастиц. Рассмотрено влияние заряда структуры на физические параметры наночастицы, определяющие свойства переноса заряда. Показано, что для качественной оценки свойств стабильности, геометрии и электронной структуры, кремниевых наночастиц можно использовать метод NDDO PM3. Представлены результаты оптимизации атомной структуры, расчет и анализ электронных характеристик кремниевых кластеров Si₂-Si₁₀ методом PM3.

Ключевые слова: полупроводниковые наночастицы, кремний, квантовохимические методы, энергетические характеристики.

Abstract. The analysis of quantum chemical methods for calculating the structural, energy and transport parameters of silicon nanoparticles. The effect of the charge structure on the physical parameters of the nanoparticles determine the properties of charge transfer. It is shown that for a qualitative assessment of the properties of stability, geometry and electronic structure of silicon nanoparticles can use the method NDDO PM3. The results of optimization of atomic structure, calculation and analysis of electronic properties of silicon clusters Si₂-Si₁₀ method PM3.

Keywords: semiconductor nanoparticles, silicon, quantum-chemical methods, the energy characteristics.

Введение

В последние десятилетия резко возрос интерес к нанообъектам самой различной природы. Это связано с тем, что частицы таких размеров обладают уникальными свойствами, отличающими их от соответствующей макрофазы [1, 2]. Использование таких свойств позволит решить наиболее острые проблемы современной электроники, связанные с приближением размеров элементов электронных схем к фундаментальному пределу, определяемому атомарным строением вещества. Это позволит развивать быстродействие и информационную емкость электронных схем в будущем. В сложившейся ситуации для дальнейшего развития электроники весьма перспективным представляется переход к схемам, построенным на базе одноэлектронных наноструктур молекулярного масштаба [3-7]. Такие схемы обеспечивают, как признанные преимущества одноэлектронных систем наноэлектроники (возможность построения цифровых систем с принципом кодирования информации одиночными электронами, предельно малое энерговыделение в таких структурах), так и достижение высокой (до 300 К) рабочей температуры.

Необходимо отметить, что самым распространенным материалом современной электроники является кремний. Естественно полагать, что различные наноформы кремния можно использовать в качестве структурных элементов наноэлектронных транзисторов, выпрямляющих элементов, а также других одноэлектронных приборах.

В данной работе представлена известная в литературе модель одноэлектронного транспорта в наноструктурах основанных на нанокластерах и наночастицах. Впервые выполнен анализ квантовохимических методов расчета структурных, энергетических и транспортных параметров кремниевых наночастиц. Выполнен анализ электронных и кинетических характеристик полупроводниковых кремниевых наночастиц с малым числом атомов (Si₂-Si₁₀). Рассмотрено влияние заряда структуры на физические параметры наночастицы, определяющие свойства переноса заряда.

Модель электронного транспорта в наноструктурах

Перенос заряда вдоль цепочки наночастиц в случае низкой плотности электронов описывается гамильтонианом [7]:

. (1)

Здесь оператор энергии возбуждения:

, (2)

где и – операторы рождения и аннигиляции возбужденного электрона с энергией в наночастице n; аналогично и – операторы рождения и уничтожения фонона с энергией .

Гамильтониан описывает перенос электрона от наночастицы (n) к наночастице (m) за счет перекрывания электронных оболочек :

. (3)

Операторы Н₃ и Н₄ описывают влияние колебаний решетки на движения электронов. Соответствующий оператору Н₃ диагональный матричный элемент (п=т), дает изменение энергии электрона, локализованного в узле п при взаимодействии с фононами:

, (4)

где g_nl – безразмерная константа электрон-фононного взаимодействия. Данный гамильтониан записан в предположении, что электрон взаимодействует лишь с одной ветвью нормальных колебаний решетки. Учет других фононных ветвей требует суммирования всех их вкладов с соответствующим статистическим весом. Оператор Н₄ записывается для случая п¹т и отражает влияние линейных колебаний на вероятность перехода с одного узла на другой.

, (5)

– константа взаимодействия.

При теоретическом описании конкретных молекулярных систем учесть все перечисленные выше составляющие гамильтониана не представляется возможным. Обычно ограничиваются рассмотрением первых двух слагаемых ( и ) гамильтониана (1), а остальными пренебрегают, для их определения необходимо рассчитать основные квантово-энергетические параметры наночастиц, участвующих в переносе заряда.

Для модельного описания переноса заряда в кластерных и молекулярных структурах удобно воспользоваться квантовомеханической моделью движения заряда в последовательности потенциальных барьеров. Ряд кластеров, отделенных друг от друга лигандной оболочкой, можно представить в виде ряда потенциальных ям, содержащих электронные уровни основного и возбужденного состояний (рис. 2) [2].

Рис. 2. Схема потенциальных ям для ряда кластеров, отделенных лигандными оболочками (энергетическим барьером или величиной емкости С). Пунктиром показаны уровни, соответствующие основному и первому возбужденному состоянию сплошными линиями – волновые функции электронов.

Рис. 3. Трехмерное изображение организации кластеров в кластерный кристалл с помощью спейсеров.

В основном состоянии валентные электроны локализованы, в возбужденном состоянии возможно туннелирование через непроводящую среду. Следовательно, электропроводимость можно менять, изменяя расстояние между кластерами за счет лигандов, которые получили название спейсеров (рис. 3).

Таким образом, транспорт электрона в наноразмерных структурах представим в виде переноса волнового пакета частицы через последовательность потенциальных барьеров.

Основными электронными и кинетическими параметрами полупроводниковых кластеров и наночастиц в применении к электронике являются [2, 4-6]:

1. Размер наночастицы и её геометрическая структура.

2. Величина энергии связи, как критерий устойчивости структуры.

3. Распределение заряда и электрического потенциала в наночастице и вблизи её поверхности.

4. Энергетическая щель между верхним заполненным и нижним свободным состоянием (HOMO-LUMO щель), являющаяся аналогом запрещенной зоны в объемных полупроводниках.

5. Величина первого потенциала ионизации (работа выхода электрона).

6. Энергия сродства электрону (энергия Ферми).

7. Электрическая ёмкость наночастицы.

Эффективная собственная емкость объектов молекулярного масштаба [5,6]:

, (6)

I₁ – первый потенциал ионизации объекта, А₁ – первое сродство к электрону.

8. Электронный и фононный спектры.

9. Характер зависимости вышеуказанных свойств от электрических и магнитных полей, а также величины температуры и механических напряжений.

10. Влияние примесей на свойства наноструктуры.

Квантово-энергетические параметры кремниевых наночастиц

В настоящее время хорошо изучена техника квантовохимических расчетов основных параметров углеродных наноматериалов [8], однако методика расчетов основных энергетических параметров наночастиц на основе неорганических материалов далеко не совершенна. Сложность расчета физико-химических свойств полупроводниковых наночастиц состоит в том, что ни один из разработанных квантовых методов расчета молекулярных и кластерных структур не позволяет с равной степенью точности вычислять весь спектр вышеуказанных энергетических и кинетических параметров.

В качестве проверки точности расчета некоторых энергетических параметров нами выполнен расчет некоторых из вышеуказанных параметров для некоторых основных электронных свойств Si₂ различными расчетными методами квантовой химии [8, 9]. Результаты представлены в табл. 1.

В приведенной ниже таблице 1 введены следующие обозначения: d(Si-Si) – межатомное расстояние в нейтральной молекуле, d(Si-Si)⁺ – межатомное расстояние в ионизированной молекуле, d(Si-Si)^– – межатомное расстояние в молекуле с одним лишним электроном (межатомное расстояние представлено в Å), E_HOMO – верхнее энергетическое заполненное состояние, DE – ширина HOMO-LUMO щели, I₁ – первый потенциал ионизации (работа выхода электрона), А₁ – первое сродство к электрону (энергетические параметры определены в eV). Необходимо отметить, что экспериментальные значения в таблице определены с погрешностью порядка 5-10% [10, 11].

Таблица 1.

Параметры молекулы Si₂, вычисленные различными методами.

Параметр нано-частицы	Метод расчета (во всех случаях UHF)
Параметр нано-частицы	INDO	PM3	HF (3-21G)	HF (6-31G*)	HF-MP2 (6-31G*)	DFT B3-LYB (6-31G*)	Экспе-римент [10, 11]
d(Si-Si)	2.03	2.30	2.37	2.25	2.26	2.34	2.25
d(Si-Si)⁺	2.14	2.48	2.42	2.41	2.41	2.38	–
d(Si-Si)^–	2.10	1.97	2.39	2.16	2.16	2.20	–
E_HOMO	-11.93	-7.61	-8.11	-8.02	-7.38	-5.62	–
DE	8.52	3.56	7.48	7.58	6.03	1.70	–
I₁	11.7	7.5	7.2	7.5	6.7	7.8	7.5
A₁	3.6	3.7	1.5	1.1	1.9	1.9	2.2

Согласно представленным в таблице 1 результатам расчета можно сделать следующие выводы.

1. Наиболее точно длину связи Si-Si определяет метод Хартри-Фока в расширенном базисе.

2. При отрыве электрона длина связи в кремниевых структурах возрастает, при захвате электрона – уменьшается. Следовательно, геометрию наноструктуры необходимо оптимизировать каждый раз при изменения её заряда.

3. Энергию сродства электрону и потенциал ионизации для большей точности расчета следует вычислять в теории DF. Однако, при оценке длины связи ошибка методов DF сопоставима с грубым методом HF(3-21G*).

4. Энергия верхнего заполненного состояния в приближении HF(6-31G*) хорошо соответствует работе выхода (теорема Купманса).

5. Расчет в теории HF-МР2 занижает значение потенциала ионизации, но энергия электронного сродства определяет наиболее точно.

6. Как показывает теория [8, 10, 11] величина HOMO-LUMO щели в атомах и молекулах близка к энергии электронного сродства. Поэтому, расчет HOMO-LUMO щели необходимо определять в теории функционала плотности, т.к. остальные методы дают значительные ошибки.

Анализируя литературные данные и полученные нами результаты, можно утверждать, что для качественной оценки свойств стабильности, геометрии и электронной структуры, кремниевых наночастиц можно воспользоваться методом PM3, как это было сделано в ряде работ по кремниевым наночастицам [12-16]. Затем геометрию структуры можно уточнить методом Хартри-Фока в расширенном базисе. Для количественного расчета основных энергетических и транспортных параметров кремниевых наночастиц необходимо воспользоваться методами HF-МР-2 и DFT. Необходимо отметить, что при практических расчетах необходимо также учитывать влияние конденсирующей наночастицы подложки [14, 15] и внешнего электромагнитного поля [16].

Вычисление энергетических характеристик при изменении заряда важно при описании взаимодействия поверхности металла с наночастицей. Если высший заполненный энергетический уровень наночастицы лежит выше уровня Ферми в твердом теле, то электрон может перейти к твердому телу, а адсорбируемый атом становится положительным (рис. 4а), если же незаполненный уровень адсорбируемой наночастицы лежит ниже уровня Ферми (рис. 4б), то электрон может перейти к наночастрице, который заряжается отрицательно. Вероятность подобных процессов определяется, высотой энергетического барьера между наночастицей и твердым телом [2].

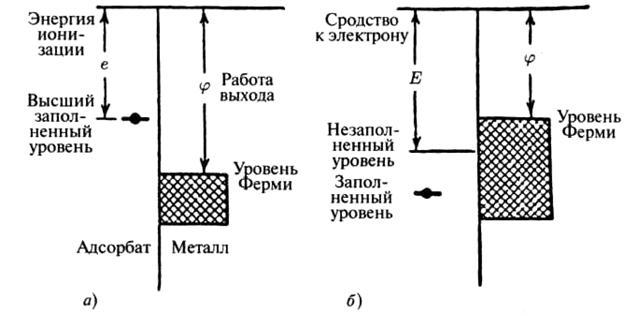
Рис. 4. Энергетические уровни адсорбируемой наночастицы и металлической поверхности. Случай (а) соответствует переходу электрона к металлу, случай (б) соответствует переходу электрона к наночастице.

Выполним расчет основных квантово-энергетических параметров малых кремниевых наночастиц Si₃-Si₁₀ . Расчет геометрии (табл. 2.) структуры энергетических свойств выполнен нами с помощью квантовохимического метода NDDO PM3 (UHF) [11, 12]. В таблице также представлены средние значения длин связей <d> для оценки размеров наночастиц [8].

В приведенной ниже таблице 3 представлены следующие величины: E_св – энергия связи, E_св/ат – удельная энергия связи, E_HOMO – верхнее энергетическое заполненное состояние, DE – ширина HOMO-LUMO щели, I₁– первый потенциал ионизации (работа выхода электрона), А₁ – первое сродство к электрону, энергетические параметры определены в eV.

Таблица 2.

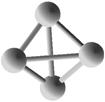
Геометрическая структура наночастиц Si₃-Si₁₀.

Si₃, <d>=2,20 Å	Si₄, <d>=2,66 Å	Si₅, <d>=2,61 Å	Si₆, <d>=2,47 Å

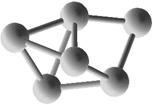
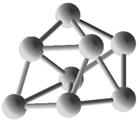
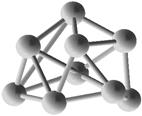
Si₇, <d>=2,55 Å	Si₈, <d>=2,52 Å	Si₉, <d>=2,77 Å	Si₁₀, <d>=2,54 Å

Таблица 3.

Энергетические характеристики наночастиц Si₃-Si₁₀.

наночастица	E_св, eV	E_св/ат, eV	E_HOMO, eV	DE, eV	I₁, eV	А₁, eV
Si₃	-7,48	-2,49	-8,22	5,61	8,03	-2,7
Si₄	-10,60	-2,65	-7,84	4,78	7,97	-3,48
Si₅	-16,17	-3,23	-8,43	4,80	8,48	-4,02
Si₆	-21.00	-3,50	-8,13	4,62	7,84	-3,81
Si₇	-26,95	-3,85	-8,64	4,47	8,07	-4,49
Si₈	-31,33	-3,92	-8,02	4,18	7,68	-4,15
Si₉	-35,54	-3,95	-8.00	5,28	7,64	-4,11
Si₁₀	-40,51	-4,05	-8,15	4,01	7,84	-4,50

Таблица 4.

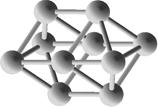
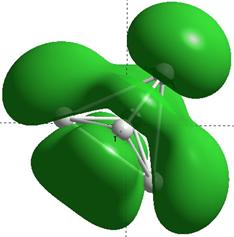
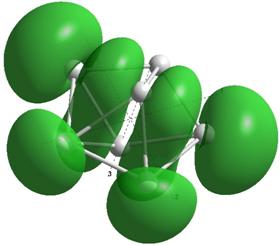
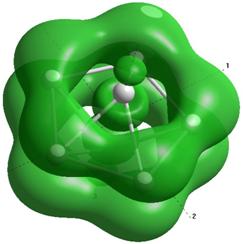
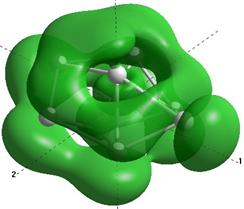
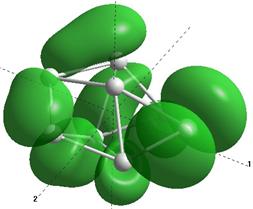
Формы верхних заполненных молекулярных орбиталей (HOMO) для кремниевых кластеров обладающими замкнутыми орбиталями, рассчитанные по методу NDDO PM3.

Si₅

Si₇

Si₈

Выводы и результаты

Выполненные расчеты позволяют сделать следующие выводы.

Все исследуемые структуры имеют отрицательные значения энергии связи, что говорит об их химической устойчивости, величина энергии связи, приходящаяся на атом (E_св/ат), возрастает с увеличением числа атомов составляющих наночастицу.

Работа выхода электрона I₁ теоретически приблизительно соответствует энергии верхнего заполненного уровня E_HOMO по абсолютной величине. Данное утверждение находится в полном согласии с теоремой Купманса [8, 11].

Величина HOMO-LUMO щели в рассматриваемых молекулярных структурах существенно отлична от энергии электронного сродства А₁, что говорит о существенном перестроении внешних электронных орбиталей после захвата дополнительного электрона.

Для оценки проводниковых свойств кремниевых наночастиц, построим определим в приближении метода РМ3 электронные HOMO орбитали для нейтрального кластера и кластера с одним дополнительным электроном (проходящему по нему). В таблице 8 представлены результаты расчетов только таких структур Si_n Si_n^- , у которых имеются замкнутые HOMO орбитали.

Как показывают выполненные расчеты, частично представленные в таблице 4, проводниковыми свойствами обладают геометрически оптимизированные наноструктуры с числом атомов 5, 7, 8. Однако, при минимальном изменении заряда структуры её проводниковые свойства исчезают.

Необходимо также указать, что при туннелировании через полупроводниковые частицы малых размеров заряд молекулы в течение некоторого времени (полупериода Т/2) изменяется на -е, вследствие чего происходит значительное изменение энергетической структуры. При этом положение вновь образовавшегося верхнего заполненного уровня не совпадает с нижним свободным для нейтрального кластера. Т.о. существует неопределенность по энергии, что связано с частотным пределом использования подобных одноэлектронных приборов на молекулярных кластерах , где – энергия нижнего свободного уровня для нейтрального кластера, – верхнего занятого уровня кластера с зарядом -е. В случае рассматриваемых кремниевых кластеров данная величина составляет ~10¹⁵Гц. Полученная частота соответствует диапазону оптических излучений и практически недостижима в реальных приборах, используемых при передаче и обработке электрических сигналов.

Таким образом, выполненный нами краткий анализ энергетических свойств наночастиц Si₂-Si₁₀ позволяет предлагать их использование в одноэлектронных приборах наноэлектроники. Управлять энергетическими и кинетическими свойствами полупроводникового нанокластера можно путем изменения атомарной структуры, заряда или внешних полей.

Литература

1. Гусев А.И. Нанокристаллические материалы: методы получения и свойства. – Екатеринбург: УрО РАН, 1998.

2. Суздалев И.П. Нанотехнология: физико-химия нанокластеров, наноструктур и наноматериалов. – М.: КомКнига, 2006.

3. Аверин Д.В., Лихарев К.К. Кулоновская блокада туннелирования и когерентные осцилляции в малых туннельных контактах. // ЖЭТФ. – 1986. – Т. 90, №2. – С. 733.

4. Солдатов Е.С., Ханин В.В., Трифонов А.С., Губин С.П., Колесов В.В., Преснов Д.Е., Хомутов Г.Б., Яковенко С.А. Одноэлектронный транзистор на основе одиночной кластерной молекулы при комнатной температуре // Письма в ЖЭТФ. – 1996. – Т.64, №7. – С.510-514.

5. Soldatov Е.S., Gubin S.P., Johansson P., Kolesov V.V., Sergeev-Cherenkov A.N., Shorokhov V.V., Sulaimankulov K.S. Correlated electron tunneling in the single-molecule nanosystems. // Phys. Low-Dim. Struct. – 2002. – V. 1-2. – P. 113-134.

6. Губин С.П., Катаева И.А., Колесов В.В., Солдатов Е.С., Трифонов А.С., Хомутов Г.Б.,Шорохов В.В. Нанофазные материалы в электронике – вещества, технология, устройства. // Нелинейный мир. – 2005. – №1-2. – C. 10-26.

7. Плотников Г.С., Зайцев В.Б. Физические основы молекулярной электроники. – М.: МГУ, 2000.

8. Минкин В.И., Симкин Б.Я., Миняев Р.М. Теория строения молекул. – Ростов-на-Дону: Феникс, 1997.

9. Кон В. Электронная структура вещества – волновые функции и функционалы плотности. // УФН. – 2002. – Т. 172, №3. – С. 336-348.

10. Бацанов С.С. Структурная химия. Факты и зависимости. М.: Диалог-МГУ. – 2000.

11. Гурвич Л.В., Караченцев Г.В., Кондратьев В.Н., Лебедев Ю.А., Медведев В.А., Потапов В.К., Ходеев Ю.С. Энергии разрыва химических связей. Потенциалы ионизации и сродство к электрону. – М.: Наука, 1974.

12. Курганский С.И., Борщ Н.А. Геометрическая и электронная структура кремниевых и кремниево-металлических наночастиц. // Известия РАН. Серия физическая. – 2004. – Т. 68, № 7. – С. 1023-1025.

13. Борщ Н.А., Переславцева Н.С., Курганский С.И. Атомная и электронная структура кремниевых и кремний-металлических наночастиц Si₂₀, Si₂₀^-, NaSi₂₀ и KSi₂₀ . // ФТП. – 2006. – Т. 40, № 12. – С. 1457-1462.

14. Филиппов В.В., Курганский С.И., Переславцева Н.С. Квантовохимическое моделирование структуры напряженных нанокристаллов кремния. // Журнал структурной химии. – 2007. – Т. 48, № 5 – С. 1016-1019.

15. Филиппов В.В., Переславцева Н.С., Курганский С.И. Квантовохимическое моделирование структуры напряженных нанокристаллов кремния на германиевой подложке. // Известия РАН. Серия физическая – 2008. – Т. 72, №9. – С. 1314-1316.

16. Филиппов В.В., Власов А.Н. Моделирование электронных свойств кремниевых наночастиц с плотной атомной упаковкой. // Известия вузов. Физика. – 2010. – № 1 – С.70-75.