“ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ” N 8, 2012

оглавление

УДК 57.012.3; 57.081.23; 616.8

 МЕТОД ПАРАМЕТРИЧЕСКОЙ АППРОКСИМАЦИИ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ НАБОРА  ДИСКРЕТНЫХ 3-D ВЕРШИН, ПРЕДСТАВЛЕННЫХ В ВИДЕ ОБЛАКА ТОЧЕК

 

В. Е. Анциперов, О. В. Евсеев, Ю. В. Обухов

Институт радиотехники и электроники им. В. А. Котельникова РАН

 

Получена 8 августа 2012 г.

 

Аннотация. Вопросы реконструкции непрерывных трехмерных распределений по дискретным пространственным данным (облакам точек) приобрели в последнее время большое значение. Это связано с целым рядом обстоятельств. К примеру, использование стандартной техники аппроксимации B-сплайнами не всегда удобно, поскольку в реальности выборочные данные, составляющие облако точек, не всегда  заданы в удобных, например,  прямоугольных областях. Другие прямые методы интерполяции (например, методы сверточного преобразования облака точек в стереолитографическую модель) могут требовать больших вычислительных ресурсов: больших размеров файлов, памяти, времени вычислений. В данной работе обосновывается новый, экономный метод параметрической аппроксимации плотности распределения набора  дискретных 3-D вершин, представленных в виде облака точек, который основан на межсрезовой интерполяции контуров следа облака в наборе параллельных сечений. Обоснование метода начинается с интерпретации проблемы аппроксимации плотности распределения как задачи построения трехмерного распределения вероятностей согласованного с определенным семейством двумерных условных распределений. Показано, что в данной интерпретации, ввиду удачного выбора параметризации, получающееся распределение хорошо описывает исходные данные и тем самым решает задачу аппроксимации. Обсуждаются практические результаты применения метода к задаче реконструкции трехмерного распределения нейронов на основе микро-изображений срезов головного мозга мышей.

Ключевые слова: Реинжиниринг, САПР (Системы Автоматизированного Проектирования) на основе моделирования, трехмерная визуализация и анализ, реконструкция распределения плотности облака точек, B-сплайны, реконструкция трехмерных распределений по изображениям сечений.

Abstract. Continuous distribution reconstruction from discrete point cloud has been receiving extensive attention recently. There are a number of reasons for that occurrence. For example, when using the conventional B-spline approximation technique, the difficulty of parameterization exists since the real point clouds are not always sampled from rectangular regions. Other direct methods (converting, for example, point clouds in stereolithography models) lead to a huge file size and require expert modeling skills. The objective of this work is to establish a new 3-D distribution reconstruction method based on intersectional approximation of cross-sectional clouds contour parameters. We present an interpretation of 3-D distribution reconstruction problem as a problem of constructing 3-D probability density which is in a certain way associated with a discrete set of 2-D conditional probability densities. Based on a good parameterization, the final density distribution is achieved with tight tolerance. One practical example – three-dimensional reconstruction neurons distribution from microscopic images of brain slices have demonstrated the feasibility of the proposed method.

Keywords: Reverse engineering, CAD (Computer Aided Design) modeling, three dimensional visualization and analysis, Point cloud density reconstruction, B-splines, methods for 3-D reconstruction of data collected from serial sections.

 

Задача аппроксимации дискретных экспериментальных данных непрерывными моделями популярна давно [1] и имеется огромное число исследований на эту тему. В теоретических исследованиях вопрос о размерности данных, как правило, не является определяющим, поскольку исследуются достаточно общие подходы и основными являются вопросы, связанные с точностью, гладкостью, другими характеристиками аппроксимаций [2]. Совсем иная ситуация имеет место в прикладных разработках, когда на первых план выдвигаются вопросы времени вычислений, объема хранения промежуточных данных, размеры используемых файлов и т.д. Здесь размерность данных оказывается принципиальной и, по существу, для одномерных, двумерных, 3D- данных эффективными оказываются совершенно разные классы аппроксимационных задач.

В отличие от хорошо развитых методов аппроксимации функций одного переменного и одномерных наблюдений (например, временных рядов), а также, хоть и в меньшей, но в значительной степени продвинутых методов аппроксимации двумерных данных, прикладные методы аппроксимации результатов трехмерных измерений находятся на сегодняшний день в стадии интенсивных исследований [3]. Это обусловлено тем, что благодаря возросшей производительности вычислительных систем стали реально реализуемыми такие сложные, взаимные технологии, как реинжиниринг и САПР (CAD) на основе моделирования. Первая технология связана с компьютеризированным сбором данных и их компактным представлением для компьютерных приложений, вторая ориентирована на создание компьютерных моделей с помощью которых осуществляется последующий анализ, синтез, усовершенствования, разработка новых моделей исследуемых объектов.

В качестве примеров широкого применения технологий реинжиниринга и компьютерного моделирования приведем технологии 3D печати [4], быстрого прототипирования [5], биометрии [6]. В качестве еще одного примера, центрального для данной статьи, отметим выполненный авторами проект «Разработка и исследование программно-алгоритмических методов автоматизации распознавания изображений нейронов и реконструкции их трехмерного распределения» (Мин. обр. и науки РФ, гос. контракт N 07.514.12.4029) [7].

В последнем проекте нами на основе концепций реинжиниринга и компьютерного моделирования было спроектировано и реализовано программно-алгоритмическое обеспечение для визуализации трехмерных распределений нейронов по данным компьютерной обработки серий двумерных срезов мозга. Отметим, что хотя мы последовательно придерживались основных рекомендаций методологии реинжиниринга/компьютерного моделирования, многие технические/алгоритмические детали пришлось либо существенно переработать,  адаптировать к проекту, либо разрабатывать заново. В итоге, как нам представляется, был получен ряд интересных, оригинальных результатов, некоторые из которых обсуждаются ниже.

Исходными данными о распределении нейронов в черной субстанции мозга являются цифровые микроизображения нейронов и волокон в специальным образом подготовленных срезах головного мозга экспериментальных животных. Cрезы имеют толщину ~20 мкм. Серия срезов одного животного может включать 60-80 микроизображений. Не останавливаясь подробно на деталях первичной подготовки  микроизображений, которые можно найти в работе [8], перейдем к обсуждению особенностей технологий реинжиниринга и компьютерного моделирования.

Технологию реинжиниринга в описываемом проекте можно разделить на два этапа: во-первых, распознавание отдельных нейронов в срезах, а, во-вторых, компактное представление этих данных для последующей обработки. Первый этап – распознавание нейронов – осуществляется на основе реализованного конвейера современных компьютерных средств распознавания изображений и описан в [9]. Результатом первого этапа являются наборы координат распознанных в срезах нейронов. Далее, отвлекаясь от специфики исходных данных, будем для общности считать, что имеющиеся данные представляют собой набор дискретных вершин в пространстве, для которой будем использовать специальный термин – облако точек (point cloud). Заметим, что это облако имеет специальную структуру: точки облака сконцентрированы в определенных параллельных плоскостях – слоях.

Второй этап реинжиниринга – компактное представление облака точек для последующей обработки – заключается в послойной 2D непрерывной аппроксимации дискретных точек непрерывными распределениями. Этот этап подробно описан в работе [10]. Здесь же кратко отметим, что в качестве аппроксимирующих распределений использовались гауссовы смеси, а в качестве метода подгонки распределений к данным – специальным образом адаптированный  EM алгоритм. Результатом второго этапа является совокупность распределений по слоям в виде гауссовых смесей со слабо пересекающимися носителями. Отметим, что, формально,  каждый элемент гауссовой смеси является параметрическим распределением – задается набором из пяти параметров, например,  двух координат центра и трех вторых моментов.

На основе результатов реинжиниринга посредством компьютерного моделирования строится уже пространственное 3D-распределение точек облака, что представляется в данном случае как дополняющая реинжиниринг технология. Ввиду выше изложенного, моделирование в данном случае подразумевает интерполяцию непрерывных распределений в слоях на межслойное пространство. Обычно такая интерполяция осуществляется посредством несложного обобщения одномерной интерполяции, например, при помощи линейной, или B-сплайновой интерполяции, на трехмерный случай [11]. Именно, пусть последовательность распределений  представляет собой соответствующие друг другу (и некоторому 3D кластеру конструируемого пространственного распределения), отдельные в каждом слое : , элементы 2D непрерывных аппроксимаций (т.е. элементы смесей). При этом мы считаем, что  – это координатная плоскость, которой параллельны все  срезов, сами срезы считаем  расположенными эквидистантно, с шагом 1, вдоль оси . Вопросы соответствия элементов смесей в соседних слоях при слабом перекрытии элементов смеси в слое не являются принципиальными, поскольку выбор ближайшего в любой разумной метрике элемента дает решение этой проблемы (в общем случае см. работу [12]).  Пусть конструируемое пространственное распределение  является интерполяцией семейства  посредством, например, B-сплайнов:

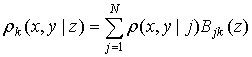 ,                                          (1)

 

где  –  последовательность  однородных  B‑сплайнов некоторого порядка  (случай соответствует линейной интерполяции ).

B-сплайны обладают рядом привлекательных свойств, которые обусловили их широкое применение в задачах приближения. В частности, все являются положительными, симметричными функциями на финитном носителе . При помощи B-сплайнов можно записать конечное разложение единицы произвольного интервала действительной оси.  Например, для   имеет место разложение:

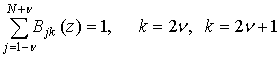 .                               (2)

 

В силу перечисленных свойств, набор  при можно интерпретировать как дискретное распределение вероятностей полной системы событий : . Ввиду того, что эта система событий оказывается несколько шире набора индексов системы , можно формально расширить систему распределений за счет фиктивных

и интерпретировать правую часть (1) как формулу полной вероятности по системе событий . Отсюда следует, что левая часть – является корректно определенной плотностью распределения вероятностей при всех .

С теоретической точки зрения конструкция (1) выглядит привлекательно простой и, как можно было убедиться, допускает простую и изящную интерпретацию. Однако с точки зрения практической реализации объем вычислений огромен. Действительно, (1) подразумевает, что межслойная интерполяция для ~ 100 слоев должна быть выполнена для всех , а это, как правило, ~106 точек! По этой причине, обычно, имея в виду (1) как теоретическую цель аппроксимации, на практике ищут те или иные подходы  моделирования, которые позволили бы снизить вычислительные ресурсы [12].

В ходе выполнения упомянутого выше проекта нами был предложен и обоснован алгоритмический метод параметрической аппроксимации, который позволяет очень экономно решить задачу компьютерного моделирования пространственного распределения набора  дискретных вершин, представленных в виде описанного выше облака точек. Главными факторами, обеспечившим эту возможность, являются следующие. Во-первых, специфика задачи – облака точек имеют в проекте “квази-одномерную” структуру – простая форма сечения облака в каждом из слоев в направлении координат  может сопровождаться существенными деформациями формы вдоль продольной оси . Во-вторых, форма представления результатов реинжиниринга в виде параметрических распределений. Из этих особенностей задачи вытекает основная идея подхода: вместо интерполяции на межслойное пространство самих распределений   (1), осуществить интерполяцию их параметров, а уже по параметрам, при любом , восстанавливать распределение .  Другими словами, вместо интерполяции распределений предлагается осуществлять интерполяцию их сжатого представления.

Изложенная выше идея выглядит перспективно: вместо ~106 процедур интерполяции по (1) предлагается осуществить всего лишь несколько, по числу параметров, процедур. Отметим, что и на самом деле, предложенный метод зарекомендовал себя в проекте с самой лучшей стороны. Однако чтобы гарантировать его эффективность и для других приложений, следует четко обосновать критерии, оценки его корректности в общей ситуации. Анализу эффективности и выработке критериев применения предложенного метода – метода параметрической аппроксимации распределений дискретных, в виде облака точек данных посвящена оставшаяся часть работы.

Пусть все плотности семейства распределений точек в слоях  принадлежат некоторому ‑параметрическому семейству распределений , , которое для наших целей удобно представить в экспоненциальной форме:

,                                          (3)

где, соответственно, . При этом для всякого  найдутся такие значения параметров , что:

.                                              (4)

Кроме этого, будем считать, что семейство  является экспоненциальным [13-14], т.е. конкретизируем вид :

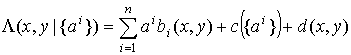.                                (5)

 

Отметим, в частности, что элементы гауссовых смесей имеют вид распределений (4-5), поэтому (5) является лишь небольшим обобщением используемого в проекте алгоритма. Подобное обобщение полезно для адаптации метода к другим приложениям, поскольку семейства распределений экспоненциального типа достаточно часто встречаются на практике [13]. Для целей последующего анализа отметим некоторые свойства экспоненциальных распределений. Во-первых, имеет место условие нормировки:

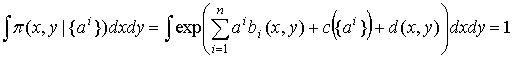.                   (6)

 

Дифференцируя условие (6) по какому-либо параметру , пoлучим:

     или     ,            (7)

 

где  означает среднее значение статистики  по распределению ,   – частную производную от  по .  Другими словами,  (7)  означает, что статистики  являются несмещенными оценками функций параметров . Аналогичным образом, дифференцируя условие (7) по какому-либо другому параметру , пoлучим следующее соотношение:

,                                    (8)

Которое можно интерпретировать как совпадение матриц ковариаций статистик  и  матрицы вторых смешанных производных от  .  Действуя подобным образом можно получить любые моменты . В частности, приведем необходимый для дальнейшего результат касающийся четвертых моментов:

.                 (9)

 

Вернемся к соотношению (1) и рассмотрим задаваемую им интерполяцию на каком-либо конкретном межслойном интервале . Ввиду отмеченной выше финитности , только  слагаемых правой части (1), где   для четных  и , дают ненулевой вклад в  (в крайних отрезках учитываются фиктивные распределения):

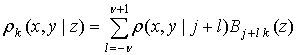,                                  (10)

 

равным образом и разложение единицы для приобретает вид -членного соотношения:

.                                         (11)

Если параметры  изменяются от слоя к слою не резко, то для плотностей (10) можно воспользоваться локальными разложениями  по приращениям параметров, например, по приращениям  :

 

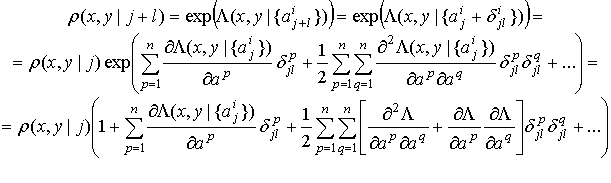                                 (12)

Подставляя (12) в (10), получим:

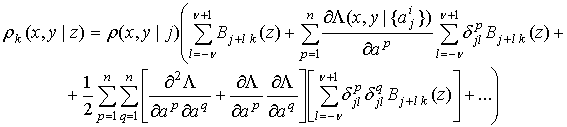.                                        (13)

Первое слагаемое во втором сомножителе (13) в силу формулы разложения единицы (11) равно единице. Сплайновая аппроксимация приращений   во втором слагаемом есть:

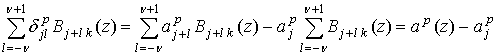,            (14)

где   -  B-сплайновая интерполяция параметров исходных распределений:

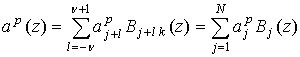.                                 (15)

Сплайновую аппроксимацию произведения приращений  в третьем слагаемом (13) преобразуем следующим образом:

,                                                (16)

В итоге, c учетом (14-16), перепишем (13) в виде:

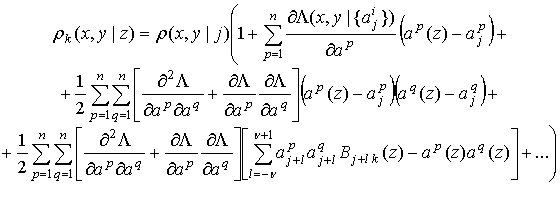.                                   (17)

Сравнивая (17) с разложением  по приращениям  ,  видим, что с точностью до членов второго порядка по , имеет место представление: 

,                                                                (18)

где остаток  имеет следующий вид:

                                      (19)

 

В соотношении (18) первое слагаемое –  есть в точности восстановленное в точке z между слоями j и j+1 по интерполированным параметрам  (15) распределение, о котором речь шла в предлагаемом методе параметрической аппроксимации. Его отличие от конструкции прямой интерполяции (1) как раз и задается остатком  (19).

Для формирования критерия отличия проанализируем главную – квадратичную по приращениям   часть , которую обозначим . Преобразуем   ее к виду, в котором отсутствуют интерполяции параметров :

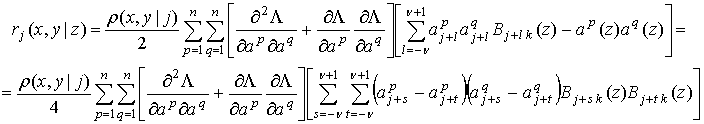                                   (20)

 Второй сомножитель во внешней сумме (20)  можно несколько упростить, если ввести локальные приближения , , где  – изменения параметров на границах рассматриваемого межслойного пространства :

 

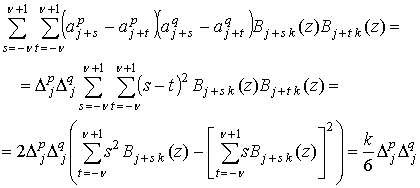  .                                                           (21)

 

Для вывода (21) помимо формулы разложения единицы (11) были использованы следующие свойства B-сплайнов [15]:

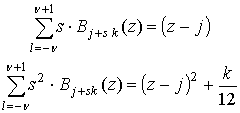
Отметим, что в выбранном приближении  выражение (21), а следовательно и  не зависят от z.  Учитывая (21) и явный вид  (5), перепишем (20) в виде:

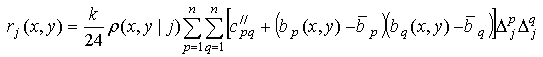.                                               (22)

Окончательно, если в качестве безразмерной величины, характеризующей относительную разность двух аппроксимаций  (1) и  (18) в области  ввести невязку , то получим:

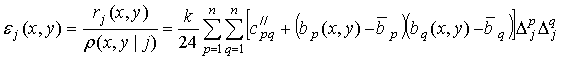.                                           (23)

Невязка  детально, в каждой точке  характеризует различие двух аппроксимаций  (1) и  (18) в сравнении с величиной самого распределения  и, тем самым, может быть выбрана в качестве оценки корректности параметрической аппроксимации. Однако, столь детальная информация для характезации  различия распределений будет избыточной если требуется иметь какую-то может быть грубую, но интегральную характеристику их отличия. Очевидно, среднее  по  для этих целей явно не подходит, поскольку в силу (8) оно будет равно нулю. Выберем поэтому, в качестве критерия корректности параметрической аппроксимации величину стандартного отклонения :

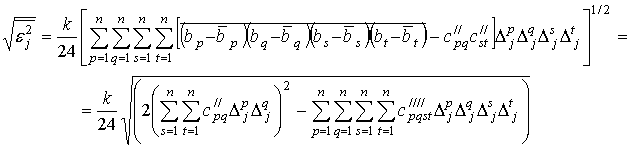,                             (24)

 

где использовано выражение (9) для четвертого момента .

Критерий (24) позволяет по имеющимся реинжинирингом данным  (определив ), , на основании выбранной модели распределений (4-5) (на основании функции параметров ) быстро оценить корректность параметрической аппроксимации в каждом из межслойных промежутков . Там, где величина критерия не превосходит допустимого уровня , , можно воспользоваться предложенным эффективным методом параметрической аппроксимации, там где нет – следует использовать прямые методы аппроксимации или методы сшивки кусков параметрической аппроксимации в местах резкого изменения параметров.

 

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации, гос. контракт № 07.514.12.4029.

 

 

Литература

1.     Арнольд В.И. Аппроксимация функций и наблюдений. Лекция, Париж, 2004, [Электронный ресурс]. Режим доступа: http://dimitrov.ucoz.ru/arnold.pdf.

2.     Ахиезер Н.И. Лекции по теории аппроксимации. М.; Наука, 1965г.

3. Ng S.C., Ismail N., Reconstruction of the 3D object model: a review. SEGi Review ISSN 1985-5672, Vol. 4, No. 2, December 2011, pp. 18-30.

4. 3D-принтеры. 3DNews Daily Digital Digest - независимое Российское онлайн-издание [Электронный ресурс]. Режим доступа: http://www.3dnews.ru/peripheral/3d-print/.

5. Wright P.K. 21st Century manufacturing. New Jersey: Prentice-Hall Inc., 2001.

6. Geng J., Zhuang P., May P., Yi S., and Tunnell D. A Fast and Accurate 3D Facial Imaging Device for Biometrics Applications. Proceeding SPIE – Biometric Technology for Human Identification, 5404, 2004, pp. 316–327.

7. Обухов Ю.В., Анциперов В.Е. и др. Система распознавания нейронов и реконструкции их трехмерного распределения по цифровым изображения срезов черной субстанции и стриатума мозга экспериментальных животных. Сб. тезисов всероссийской конференции «Проведение научных исследований в области обработки, хранения и защиты информации». Москва, 2011. – С. 97-99.

8. Хаиндрава В.Г., Ершов П.В., Анциперов В.Е., Обухов Ю.В. и др. Оптимизация количественного анализа дофаминергических нейронов в черной субстанции у мышей при моделировании болезни Паркинсона. – Цитология, 2010. - Т. 52, № 6. - С. 423-430.

9. Gurevich I.B., Kozina E.A., Myagkov A.A., Ugryumov M.V., Yashina V.V. Automating Extraction and Analysis of Dopaminergic Axon Terminals in Images of Frontal Slices of the Striatum. Pattern Recognition and Image Analysis: Advances in Mathematical Theory and Applications, 20(3). 2010. – pp. 349-359.

10. Обухов Ю.В., Анциперов В. Е., Евсеев О. В. Система компьютерной реконструкции 3D-распределений нейронов на основе априорной морфологической информации и серий изображений 2D-срезов головного мозга. ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ, электронный журнал, ISSN 1684-1719, N 7 - июль 2012 г., [Электронный ресурс]. Режим доступа: http://jre.cplire.ru/jre/jul12/5/text.html.

11. Yuwen S.,·Dongming G.,· Zhenyuan J., Weijun L. B-spline surface reconstruction and direct slicing from point clouds. Int J Adv Manuf Technol, 27, 2006, pp. 918–924

12. Ju Т., Warren J., Carson J.  Building 3D surface networks from 2D curve networks with application to anatomical modeling. Visual Comput 21, 2005, pp/ 764–773.

13. Кендалл М., Стьюарт А. Статистические выводы и связи. том 2, М.: Наука, 1973.

14. Кокс Д., Хинкли Д. Теоретическая статистика. М.: Мир, 1978.

15. Schoenberg I. J.  Cardinal Spline Interpolation. CBMS, SIAM (Philadelphia), 1973.