Удк 621.396.697
Формирование тестового массива отсчётов ыходного сигнала радиолокационного датчика
с непрерывным излучением для имитации движущейся точечной цели
А. Н. Детков, С. И. Жеребцов, И. А. Макаров
ОАО «НПК НИИДАР» г. Москва
Получена 27 июня 2013 г.
Аннотация. Предложен алгоритм формирования тестового массива отсчётов сигнала, имитирующего отклик на выходе частотно-зависимой части бортового радиолокационного датчика (БРЛД) непрерывного излучения от движущейся точечной цели при облучении её зондирующим периодическим сигналом с линейной частотной модуляцией (ЛЧМ). Получено аналитическое выражение «разностной» частоты и фазы имитируемого сигнала, а также его спектр. Рассмотрены вопросы генерации последовательности цифровых отсчётов и учёта случайного значения начальной фазы зондирующего сигнала в начале периодов модуляции. Полученный алгоритм может быть использован в акусто- и гидролокации, а также для расчёта опорных функций при синтезировании апертуры антенны в РЛС с непрерывным излучением.
Ключевые слова: радиолокационный датчик непрерывного излучения, тестовый сигнал, линейная частотная модуляция.
Abstract. The algorithm of formation of a test file of readout of the signal simulating the response on an exit of a frequency-dependent part of the onboard radar-tracking gauge of continuous wave from the moving dot target at an irradiation by its probing periodic chirp signal is offered. Analytical expression of a difference of frequencies and phases of a simulated signal, and also its spectrum is received. Questions of generation of sequence of digital readout and the account of casual value of an initial phase of a probing signal in the beginning of the periods of modulation are considered. The received algorithm can be used in akusto - and hydrolocations, and also for calculation of basic functions at CW SAR.
Keywords: the onboard radar-tracking gauge of continuous wave, a test file of the signal simulating, chirp signal.
Введение
Для создания комплексов типа БРЛД [1, 2], безусловно, важным моментом является наличие так называемых тестовых записей сигналов, по которым можно было бы проводить в дальнейшем калибровку и испытания аппаратуры. Это позволяет при создании аппаратного образца БРЛД существенно оптимизировать временные, финансовые и материальные затраты на всех этапах его проектирования. Вопрос снижения затрат на испытательные полёты также может быть решен за счёт увеличения доли имитационного моделирования [3]. При этом в качестве объекта моделирования выступают реальные устройства из состава БРЛД непрерывного излучения, внешние условия и процессы обработки информации, воспроизведение которых необходимо для успешного проведения стендовой отработки.
Наиболее сложной задачей при проведении моделирования БРЛД является формирование тестовых записей сигнала, который бы адекватно отражал физические процессы, протекающие при сопровождении движущейся цели радиолокатором. В настоящее время в доступной научной литературе такая задача не формулировалась, примеры таких тестовых сигналов, их основные характеристики, а также алгоритмы их генерации отсутствуют.
Особенностью БРЛД непрерывного излучения зондирующих сигналов с ЛЧМ, которую обязательно необходимо учитывать при моделировании, является то, что при сопровождении движущейся цели измеряется «фиктивная» дальность до неё, определяемая как задержкой зондирующего сигнала по трассе БРЛД – цель, так и доплеровским сдвигом частот биений.
Целью статьи является синтез тестового сигнала, имитирующего на выходе частотно-зависимой части БРЛД непрерывного излучения отклик от движущейся точечной цели при облучении её зондирующим сигналом с пилообразной ЛЧМ при условии точного учёта доплеровского смещения частот биений.
Модель сигнала биений на выходе БРЛД при использовании несимметричной периодической ЛЧМ
Общая геометрия движущейся цели и структура БРЛД показаны на рис. 1. Положим, что цель движется прямолинейно с постоянной скоростью перпендикулярно направлению на БРЛД, которая совпадает с электрической осью диаграммы направленности антенной системы. Предполагается также, что величина смещения цели за время задержки зондирующих сигналов на порядок меньше характерных размеров цели, поэтому этим смещением можно пренебречь.
Введём обозначения для математических символов, используемых в статье:
·
– начальная
несущая частота сигнала с ЛЧМ;
·
– девиация
частоты сигнала с ЛЧМ;
· B – коэффициент, определяющий скорость изменения частоты сигнала с ЛЧМ;
·
– период
модуляции сигнала с ЛЧМ;
· t – текущее время, которое принимает отрицательные значения при приближении цели к передатчику и положительные – при удалении от него;
·
–
время задержки зондирующего сигнала;
· c – скорость света;
· v – скорость цели;
·
– минимальное
расстояние от БРЛД до цели по траверзе;
·
–
время нахождения цели в диаграмме направленности антенны (ДНА) БРЛД;
·
– ширина ДНА БРЛД в горизонтальной
плоскости на уровне 3 дБ.
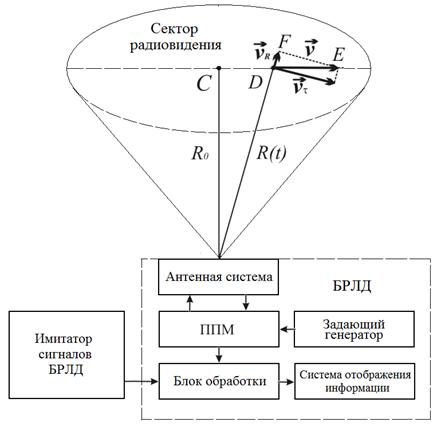
Рис.1. Геометрия радиовидения движущейся точечной цели и структура БРЛД.
Рис.2. Вид периодического пилообразного несимметричного непрерывного зондирующего ЛЧМ сигнала.
Для радиолокаторов,
использующих периодический несимметричный закон изменения ЛЧМ (рис. 2), несущая
частота зондирующего сигнала 
изменяется в соответствии
с выражением:
где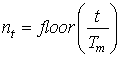 
, 
–
функция, принимающая минимальное целое значение.
Рассмотрим положение цели в произвольный момент времени t, считая, что в начальный момент времени t = 0 цель находится на траверзе.
Частота сигнала, отраженного от движущейся цели изменяется в силу эффекта Доплера и определяется выражением [4]:
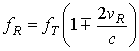, (2)
где 
– частота
отражённого электромагнитного излучения, 
– модуль радиальной
составляющей скорости цели, определяемой как:
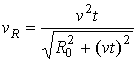, (3)
где 
.
С учётом выбора направления движения цели как показано на рис. 1 (слева направо) и выражения (3) формулу (2) можно переписать в виде:
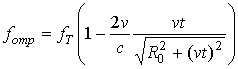. (4)
Поскольку в рассматриваемом случае частота зондирующего сигнала изменяется по закону ЛЧМ, то зависимость частоты отраженного от цели сигнала от времени с учётом (1), (4) может быть записана в виде:
.
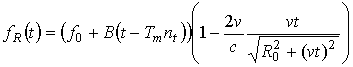Кроме того, отражённый от цели сигнал приходит задержанным по времени на величину:
.
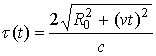В приёмно-передающем модуле (ППМ) БРЛД зондирующий сигнал через аттенюатор поступает на смеситель, где он перемножается с отражённым от цели сигналом. Таким образом, формируется сигнал частоты биений (разностной частоты):
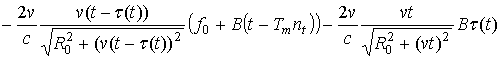, (5)
где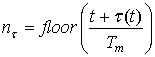 
.
Выражение (5) можно существенно
упростить. В самом деле, первое слагаемое в дальнейшем можно не учитывать,
поскольку оно отражает появление скачков частоты биений на короткое время 
, величина которого определяется произведением
и в дальнейшем подавляется в фильтре
нижних частот (ФНЧ). Последнее слагаемое в (5) имеет порядок малости 
и при оговорённых выше условиях и малых даёт крайне малый вклад, как в величину 
,
так и в накопленный за время наблюдения набег фазы рассматриваемого сигнала. По
этой же причине можно пренебречь во втором слагаемом зависимостью от времени задержки
сигнала .
Таким образом, после прохождения ФНЧ фактически выделяется следующий сигнал частоты биений:
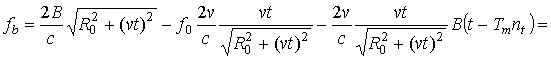
Отметим физический смысл каждого из слагаемых в (6).
Первое слагаемое
− статическая «дальностная»
составляющая, обусловленная возникновением разности частот между линейно изменяющимся
по частоте зондирующим сигналом и принятым сигналом, задержанным на время , в случае если бы цель не двигалась
(фактически учитывается текущая дальность от БРЛД до цели). Слагаемое зависит
от параметра ЛЧМ и не зависит от текущего значения частоты зондирующего сигнала
и скачков частоты при смене периодов модуляции, т.к. эти скачки частоты подавляется
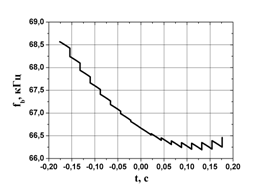
в ФНЧ. Типичный вид зависимости компоненты частоты
сигнала биений от времени 
наблюдения цели в
секторе радиовидимости приведён на рис. 3.
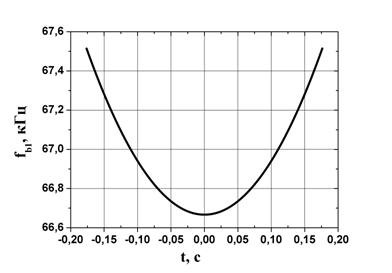
Рис.3. Зависимость компоненты частоты сигнала биений от времени наблюдения цели в секторе радиовидимости.
Параметры модели: =10 ГГц, B=100 ГГц/с,
= 100 м, v=100 м/c, = 200.
Второе слагаемое
− статическая доплеровская
составляющая, обусловленная результатом умножения частоты на
доплеровский коэффициент
.
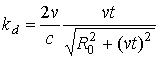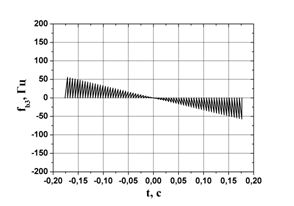
Эта составляющая зависит
от текущего положения цели и от скорости её перемещения. Типичный вид
зависимости компоненты 
частоты сигнала биений от
времени 
наблюдения цели в секторе радиовидимости
приведён на рис. 4. Заметим, что, хотя зависимость функции 
от
времени в целом нелинейная, но на практике при достаточно больших расстояниях
до цели и узких ДНА зависимость 
от времени близка к линейной.
Рис.4. Зависимость компоненты частоты сигнала биений от времени наблюдения цели в секторе радиовидимости.
Параметры модели: =10 ГГц, B=100 ГГц/с, = 100 м, v=100 м/c, = 200.
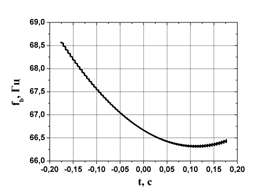
Третье
слагаемое 
− динамическая
доплеровская составляющая, обусловленная результатом умножения доплеровского
коэффициента 
на изменяющуюся в пределах девиации часть
частоты зондирующего сигнала. Кроме того это слагаемое имеет периодически изменяющийся
множитель. Доплеровский же коэффициент представляет собой гладкую функцию от
времени, не зависящую от наличия модуляции зондирующего сигнала. Типичный вид
зависимости компоненты частоты сигнала биений от
времени наблюдения цели в секторе радиовидимости
приведён на рис. 5 для различных периодов модуляции: 
=
20 мс (рис. 5а) и = 5 мс (рис. 5б).
Видно, что с ростом периода модуляции вклад данной составляющей в частоту
сигнала биений возрастает.
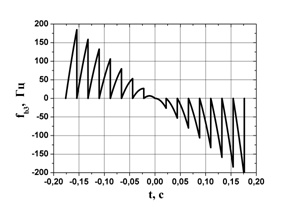
На рис. 6 приведены
итоговые зависимости частот сигналов биений 
от времени
при одних и тех же параметрах модели, за
исключением периодов модуляции ЛЧМ сигнала: = 20
мс (рис. 6а) и = 5 мс (рис. 6б). Видно,
что вклад каждого слагаемого может быть существенным и зависит от таких параметров
модели как дальность до цели, скорости цели, частота зондирующего сигнала, скорости
изменения частоты и периода повторения ЛЧМ сигнала. Важно заметить, что
итоговая зависимость частоты сигнала биений от времени принципиально
несимметрична относительно момента времени t
=
0
из-за доплеровских составляющих.
|
|
|
|
а) |
б) |
|
|
Рис.5. Зависимость компоненты |
||
|
|
|
|
а) |
б) |
|
|
Рис.6. Зависимость частоты сигнала
биений |
||
Фаза сигнала биений
При решении задачи формирования тестового сигнала БРЛД важно отметить, что для случая одной точечной цели при использовании зондирующего сигнала с ЛЧМ на выходе ФНЧ БРЛД формируется один гармонический сигнал, в котором информация о цели содержится в его относительно медленно меняющейся фазе. Это позволяет утверждать, что для решения задачи формирования тестового сигнала достаточно сначала найти фазы искомого сигнала биений для любого момента времени, после чего для получения значений отсчётов самого тестового сигнала произвести подстановку полученных значений текущей фазы в гармоническую функцию.
Следует отметить, что
частота биений испытывает скачки на границах смены периодов модуляции, в то
время как фаза сигнала биений на выходе ФНЧ меняется непрерывно, без скачков и
не зависит от случайной начальной фазы на каждом периоде модуляции. Поэтому для
получения фазы сигнала биений для любого момента времени необходимо проинтегрировать
частоту биений по времени. Пределы интегрирования следует выбирать из геометрии
задачи: нижний предел равен 
, верхний предел равен t,
где 
.
Первое слагаемое фазы сигнала биений определяется как интеграл от первого слагаемого выражения (6):
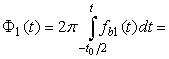
. (7)
Аналогично для второго слагаемого фазы получаем:
. (8)
Для вычисления 
разобьём
выражение 
на два слагаемых:
,
.
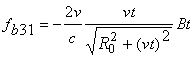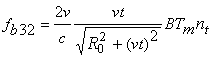Соответственно, зависимость фазы от времени для третьего слагаемого сигнала биений представим в следующем виде:
.
Фаза 
определяется
путём интегрирования слагаемого 
:
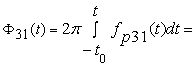
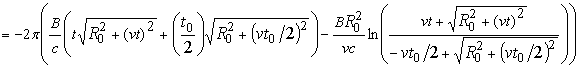. (9)
Фаза
определяется путём интегрирования
слагаемого 
:
.
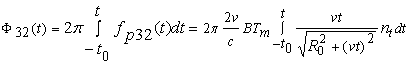Интеграл в последнем выражении можно
взять аналитически, если разбить интервал времени 
на 
«целых» отрезков длиной и
один оставшийся «нецелый» отрезок 
, где 
.
В результате такого разбиения итоговое значение компоненты фазы будет рассчитываться как сумма фазовых
набегов на каждом таком интервале времени. На каждом из таких отрезков
целочисленная функция 
принимает постоянное
значение и может быть вынесена за знак интеграла. Например, 
для
произвольного i-го целого отрезка 
, где 
. Поэтому вклад в фазовый набег на i-ом
целом отрезке составит
.
В то же время для
последующего за ним «нецелого» отрезка 
функция
и
вклад в общий фазовый набег на i-ом отрезке составит
.
Выражение для компоненты фазы 
получается с переменным (зависимым от
времени t) верхним индексом оператора суммирования:
. (10)
Окончательное выражение фазы сигнала
биений 
получим, сложив последовательно все компоненты
из (7) − (10):
, (11)
где
, 
.
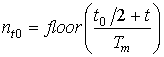Формирование отсчётов тестового сигнала
Полученное в (11)
выражение текущего значения фазы является основой
для формирования требуемого комплексного тестового сигнала, который в общем
виде можно представить либо в экспоненциальной, либо в тригонометрической форме
, (12)
где 
, 
−
амплитуда формируемого тестового сигнала.
Окончательный вид тестового сигнала должен соответствовать последовательности отсчётов сигнала биений с выхода АЦП. Поэтому непрерывный процесс (12) должен быть подвергнут дискретизации во времени и квантованию по уровням, а затем кодированию двоичным кодом. С учётом большого числа уровней квантования шумом квантования можно пренебречь и (12) будет представлять собой дискретный процесс в виде косинусной и синусной составляющих:
, 
,
(13)
где 
– интервал
дискретизации АЦП, выбранный в соответствии с теоремой В.А. Котельникова; k
– номер отсчёта АЦП.
Результаты моделирования
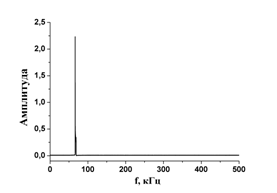
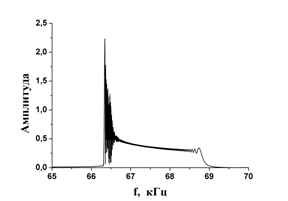
На рис. 7 представлены характерные спектры сигнала биений для последовательных временных выборок длиной около 10% от всей длины тестовой последовательности, соответствующей времени нахождения движущейся цели в ДНА. Видно смещение спектра по частоте, отвечающее при заданных параметрах задачи сначала сближению цели с БРЛД, а затем удалению от него. На рис. 8 приведён спектр полной тестовой последовательности: в обзорном спектральном окне (рис. 8а) и в «узком» спектральном окне (рис. 8б).
Заключение
В аналитическом виде решена задача фазово-частотных отношений формируемых отсчётов тестового сигнала БРЛД непрерывного излучения для имитации движущейся цели. Любые воздействия на тестовый сигнал – амплитудные, помеховые и аппаратурные – могут накладываться на уже готовую тестовую реализацию в любой комбинации, что зависит от конкретной цели моделирования.
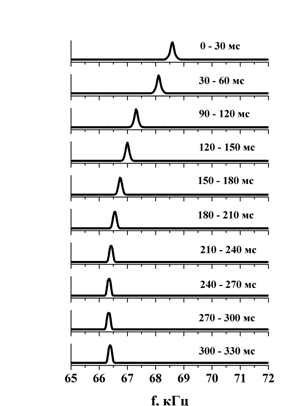
Рис.7. Полное время записи сигнала
соответствует времени нахождения цели в секторе радиовидимости. Спектры
разностных сигналов на последовательных временных интервалах длительностью 30
мс. Параметры модели: =10 ГГц, B=100
ГГц/с, = 100 м, v=100 м/c, = 200, =
1 мс.
а) б)
Рис.8. Спектр разностного сигнала на полном интервале времени записи: а) – во всём диапазоне частот полосы пропускания фильтра, б) – в ограниченном спектральном диапазоне частот. Полное время записи сигнала соответствует времени нахождения цели в секторе радиовидимости.
Параметры модели:
=10 ГГц, B=100 ГГц/с, = 100 м, v=100 м/c, = 200, =
1 мс.
При необходимости представленная модель может быть дополнительно расширена за счёт включения в неё других факторов воздействия на формируемый тестовый сигнал, например, изменение амплитуды сигнала, связанное с зависимостью от: дальности до цели, эффективной поверхности рассеяния цели, а также от характеристик диаграммы направленности антенны.
Также данная модель формирования тестового сигнала на выходе БРЛД от точечной цели может быть расширена до модели формирования такого сигнала от нескольких распределённых целей или от одной протяжённой цели, которую можно разбить на множество точечных излучателей. При этом итоговый сигнал может быть получен в соответствии с предложенной моделью как сумма сигналов от всех точечных излучателей.
Предложенный алгоритм формирования тестового сигнала биений является универсальным и может применяться в акусто- и гидролокации, а также может быть использован для расчёта опорных функций при синтезировании апертуры антенны в РСА с непрерывным излучением [5].
Литература
1. Радиолокационная система дистанционного зондирования земли. Патент РФ № 2480788 / Прилуцкий А.А., Детков А.Н., Ницак Д.А. Приоритет от 10.07.2012 г.
2. Прилуцкий А. А., Детков А. Н., Жеребцов С. И. и др. Радиолокационный вертолетный датчик миллиметрового диапазона радиоволн с непрерывным излучением // Успехи современной радиоэлектроники. 2012. № 2. С.26 − 33.
3. Сенцов А.А. Программно-аппаратные средства обеспечения стендовой отработки бортовх РЭК // Вопросы радиоэлектроники. Радиолокационная техника. 2010. Вып. 1. С. 145 – 154.
4. Васин В.В., Власов О.В., Дудник П.И., Степанов Б.М. Авиационная радиолокация. – М.: ВВИА им. проф. Н.Е. Жуковского, 1964. – 584 с.
5. Детков А. Н. Оптимальный алгоритм формирования радиолокационных изображений в РСА с непрерывным излучением // Успехи современной радиоэлектроники. 2011. № 4. С.46 − 52.