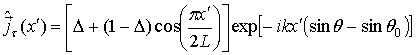УДК 621.396.679.4

СТАБИЛИЗАЦИЯ ДИАГРАММЫ НАПРАВЛЕННОСТИ ЗЕРКАЛЬНОЙ АНТЕННЫ В ПОЛОСЕ ЧАСТОТ

 

Н. И. Бобков ¹, Д. Д. Габриэльян ²

¹ ОАО «ВНИИ «Градиент», ² ФГУП «Федеральный научно-производственный центр «РНИИРС», г. Ростов-на-Дону
 

Получена 12 февраля 2013 г., после доработки - 31 июля 2013 г.

 

Аннотация. В статье представлен метод синтеза амплитудно-фазового распределения токов на поверхности отражателя зеркальной антенны с сохранением заданных характеристик диаграммы направленности неизменными в широкой полосе частот. Приведены основные соотношения и на примере параболического цилиндра исследованы закономерности поведения амплитудно-фазового распределения, обеспечивающего стабилизацию параметров диаграммы направленности в полосе частот три октавы.

Ключевые слова: Зеркальная антенна, параболический цилиндр, отражатель, амплитудно-фазовое распределение, поверхностные токи, диаграмма направленности.

Abstract. The article presents the method of synthesis of the current’s amplitude-phase distribution on the dish antenna’s reflection surface, that preserves the given constant pattern characteristics over a wide frequency band. The fundamental relations are presented and properties of the amplitude-phase distribution, which supports stability characteristics of the radiation pattern over the three-octave frequency band, are investigated on the example of a parabolic cylinder.

Keywords: reflector antenna, parabolic cylinder, reflector, amplitude phase distribution, surface currents, radiation pattern.

 

Введение.

Одними из наиболее сложных вопросов современной теории и техники антенн, в частности зеркальных антенн, являются вопросы разработки широкополосных антенных систем, диаграммы направленности (ДН) которых сохраняют свои параметры в широкой полосе частот. Такие антенны могут применяться в различных радиоэлектронных комплексах, а общим требованием для них является сохранение параметров ДН в полосе частот 2…4 октавы. В [1-4] предложен метод построения многолучевых сверхширокополосных зеркальных антенн, основанный на применении частотнозависимых радиопоглощающих покрытий на рабочей поверхности отражателя. Эффект стабилизации параметров ДН обеспечивается за счет совместного использования направленных свойств облучателей и радиопоглощающего покрытия с частотнозависимыми характеристиками, для которых должны соответственно выполняться следующие требования:

‑  ширина ДН облучателей с ростом частоты должна монотонно убывать;

‑ отклонение амплитудно-фазового распределения (АФР) токов, возбуждаемых облучателем на поверхности отражателя, от требуемого на соответствующей частоте для формирования ДН с заданными характеристиками должно корректироваться путем применения частотно-селективных радиопоглощающих покрытий.

Характеристики сверхширокополосных рупорных облучателей в настоящее время достаточно подробно исследованы и рассмотрены, например, в работах [5-7]. Методика расчета параметров частотнозависимого покрытия отражателя рассмотрена в [8]. Метод анализа характеристик излучения сверхширокополосной многолучевой зеркальной антенны изложен в [9]. Там же приведен пример практической реализации такой антенны, предназначенной для работы в девятикратном диапазоне частот. Что касается покрытий, то  разработанные в последние годы радиопоглощающие покрытия на основе кремнийорганических связующих обладают высокой степенью адгезии к металлам и повышенными физико-механическими характеристиками и могут обеспечить надежную работу антенн в широком интервале температур при воздействии вибрации и других механических факторов. Таким образом, в настоящее время имеются практически все теоретические и технологические предпосылки для построения сверхширокополосных многолучевых зеркальных антенн на основе предложенного метода. Однако среди теоретических вопросов в настоящее время недостаточно исследованы основные закономерности изменения АФР поверхностных токов на отражателе, обеспечивающего в полосе частот формирование ДН с неизменными заданными параметрами с учетом характеристик облучателей и формы отражателя.

Известен ряд работ, в которых излагаются основы синтеза амплитудно-фазового распределения по заданной (заранее известной) комплексной ДН [10-14]. Основное внимание в этих работах уделяется синтезу АФР для криволинейных излучателей и плоских АР. В то же время вопросы синтеза АФР на отражателях произвольной формы по ограниченному набору заданных параметров ДН (ширина и ориентация главного лепестка, огибающая боковых лепестков) требуют проведения отдельных исследований. Таким образом, рассматриваемые в настоящей статье вопросы синтеза АФР на криволинейной поверхности являются актуальными в практическом плане и имеют несомненный интерес с теоретической точки зрения.

Цель статьи – разработка метода синтеза АФР на произвольной поверхности по параметрам заданной ДН и исследование частотных зависимостей АФР, обеспечивающего сохранение параметров ДН в полосе частот.

 

1.     Постановка задачи.

  В рассматриваемой постановке задачи синтеза АФР на криволинейной поверхности будем считать заданными:

‑ форму и размеры поверхности  отражателя, удовлетворяющей условиям Ляпунова [15];

‑ параметры требуемой векторной ДН, определяемые шириной и ориентацией главного максимума ДН, а также пространственным распределением огибающей боковых лепестков.

Необходимо найти закон распределения плотностей поверхностных электрических  токов на поверхности отражателя  (- и -касательные орты локальной системы координат , - и -координаты отсчитываются вдоль соответствующих координатных линий), обеспечивающий формирование ДН, параметры которой имеют минимальное среднее квадратичное отклонение от заданных.

Рассматриваемая постановка задачи отличается от известных [12-14] заданием только ряда параметров требуемой ДН. Это не позволяет напрямую использовать хорошо известные методы синтеза АФР по заданной ДН, при использовании которых необходимо иметь заданную комплексную или амплитудную диаграмму направленности. В связи с этим первым шагом решения поставленной задачи является синтез АФР  на некоторой вспомогательной поверхности , обеспечивающего формирование ДН с требуемыми параметрами. Такую ДН в дальнейшем будем называть вспомогательной. Результатом этого является возможность описания требуемой ДН в виде функции , которая соответствует не только требуемым параметрам, но и детально  описывает ДН с заданными параметрами (определяет угловые положения и уровни боковых лепестков, нули ДН). В дальнейшем это дает возможность перейти к решению задачи синтеза АФР на произвольной поверхности  по заданной ДН . Данный подход применительно к решению задачи синтеза амплитудно-фазового распределения в раскрыве плоской антенной решетки рассматривался в работе [16].

В качестве вспомогательной поверхности наиболее просто использовать круг или прямоугольник, размеры которых определяются параметрами ДН. При этом для нахождения АФР  на  возможно использование хорошо известной взаимосвязи параметров распределения токов и ДН [17] или изложенного в [18] алгоритма определения АФР в линейной антенне по заданным в одном сечении параметрам ДН.

 

2.     Решение задачи синтеза.

  На основе достаточно простых преобразований компоненты ДН полей, возбуждаемых распределенными на поверхности  токами, можно представить в виде [15]

,                                                    (1)

.                                            (2)

 

В соотношении (1) ,  и аналогичные сомножители из (2) представляют элементы тензорной функции Грина, определяющие вклад касательных к поверхности отражателя - и - компонент электрических токов в - и - составляющие ДН.

Для нахождения неизвестного распределения плотности электрического тока на поверхности отражателя, обеспечивающего формирование ДН с минимальным средним квадратическим отклонением параметров от заданных, потребуем совпадения формируемой и заданной ДН в  направлениях, определяемых углами , ()

 

                                                                          (3)

 

Система уравнений (3) представляет собой систему интегральных уравнений (ИУ) Фредгольма первого рода относительно неизвестных распределений компонентов токов  и . Для решения данной системы ИУ разделим поверхность  отражателя на элементы  (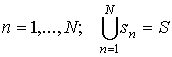) и представим неизвестное разложение компонент токов с помощью кусочно постоянных функций следующим образом

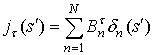,                                                                                       (4)

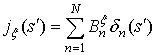,                                                                                       (5)

 

где

   

 

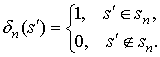
Выбранная аппроксимация неизвестного распределения поверхностных токов позволяет свести решение системы интегральных уравнений к решению системы линейных алгебраических уравнений (СЛАУ)

.                                                                                                   (6)

В соотношении (6) вектор-столбец , элементами которого являются искомые коэффициенты разложения токов, имеет размерность , вектор-столбец , элементами которого являются комплексные значения - и -компоненты ДН, имеет размерность . Элементы матрицы  определяют соответственно вклад компонент поверхностного электрического тока -го элемента поверхности отражателя () в - или -компоненты ДН в -м направлении ().

В развернутом виде матричное уравнение (6) имеет вид

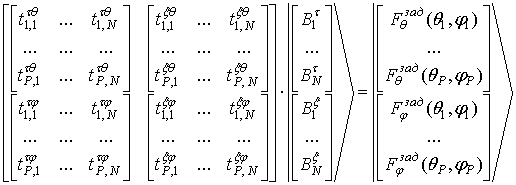,                  (7)

где , , , .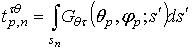

 

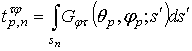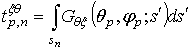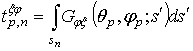При выполнении условия  получаемое решение СЛАУ (7) будет давать наилучшее приближенное решение по методу наименьших квадратов [19]. Поскольку ранг матрицы  равен , решение задачи амплитудно-фазового синтеза антенной решетки при этом может быть найдено в виде [19]

,                                                                                                  (8)

где  ‑ псевдообратная матрица для матрицы , определяемая выражением [19]

.                                                                                       (9)

В выражении (9)  ‑ матрица, транспонированная и комплексно-сопряженная по отношению к . Параметр регуляризации  выбирается из условия компромисса между точностью синтеза ДН и гладкостью получаемого амплитудно-фазового распределения.

Соотношения (3)-(8) вместе с алгоритмом формирования  описывают метод синтеза АФР по заданным параметрам ДН на произвольной криволинейной поверхности. Определение АФР для различных электрических размеров отражателя и неизменной в частотном диапазоне  позволяет определить частотную зависимость АФР, обеспечивающую стабилизацию параметров формируемой ДН в диапазоне частот.

 

3. Пример синтеза АФР в широкой полосе частот.

 Проанализируем возможность сохранения характеристик ДН на различных частотах путем изменения параметров АФР по поверхности криволинейного отражателя. Рассмотрим частный, но важный с практической точки зрения случай синтеза АФР на поверхности цилиндрического параболоида по заданной ДН. Поперечное сечение отражателя  описывается уравнением

,   .                                                                                     (10)

В качестве заданной будем рассматривать ДН, формируемую на нижней частоте  электрическим током, распределенным по закону

                                    (11)

 

на вспомогательной плоской поверхности , совпадающей с раскрывом антенны (отрезок прямой ). При проведении расчетов параметры отражателя принимались равными ,  ( ‑ скорость распространения электромагнитных волн в свободном пространстве).

На рисунках 1-4 и 5-8 приведены синтезированные амплитудно-фазовые распределения и формируемые ДН для частот , , , для случая  постоянного амплитудного распределения на вспомогательной поверхности, т.е. при Δ=1. При этом первая группа рисунков иллюстрирует результаты, полученные в случае неотклонённого главного максимума  (), вторая группа рисунков – при отклонении главного максимума на угол .

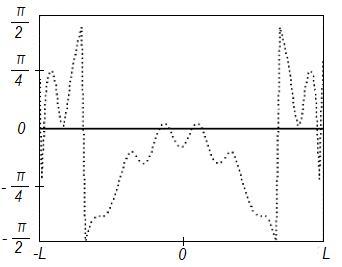
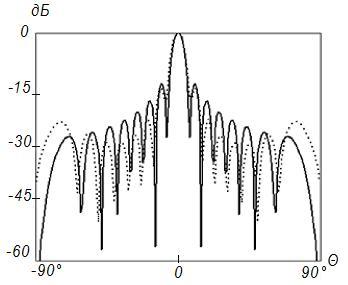
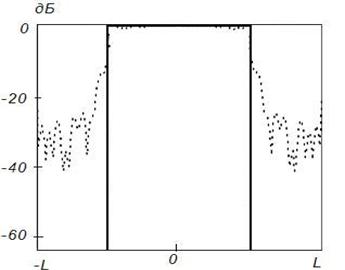
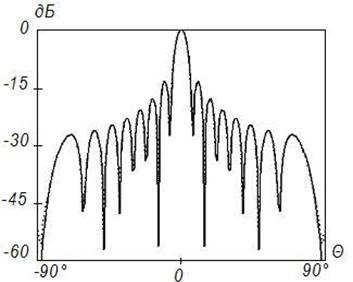
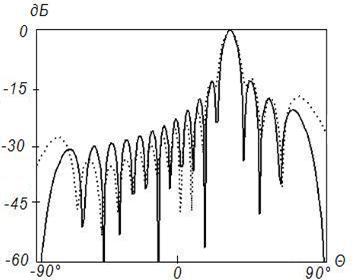
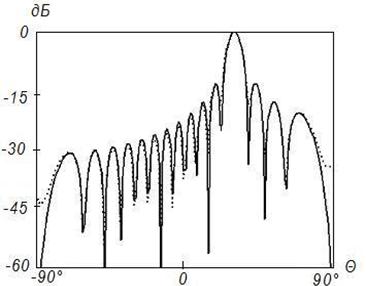
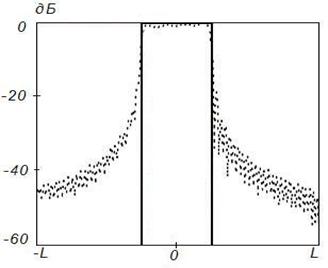
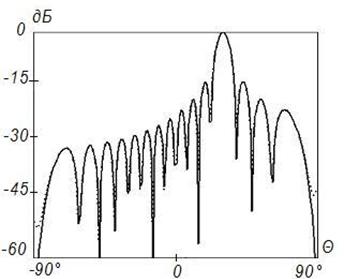
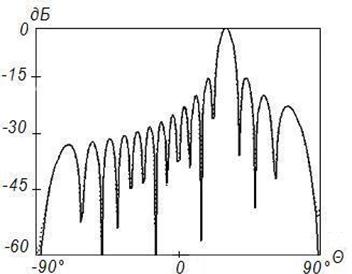
Во всех случаях на рисунках с индексом «а» представлены амплитудные распределения тока по поверхности отражателя, на рисунках с индексом «б» – фазовые распределения токов по поверхности отражателя и на рисунках с индексом «в» ‑ синтезированные ДН (штриховая линия). Заданная ДН и АФР на вспомогательной поверхности на этих рисунках показаны сплошной линией. Возрастание частоты при неизменных геометрических размерах отражателя приводит к пропорциональному увеличению его электрических размеров. В то же время электрические размеры поверхности, используемой для формирования вспомогательной ДН, остаются неизменными.

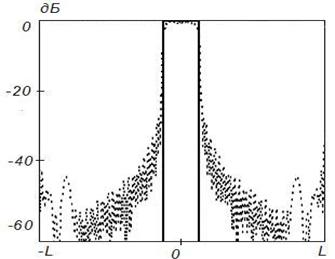
          Анализ приведенных результатов показывает, что синтезируемое АФР хорошо совпадает с заданным. В частности, на частоте  модуль АФР является практически  постоянным  в  пределах  отражателя  (рисунок 1,а),  а  на  более высоких частотах – в пределах центральной области отражателя, равной по размерам вспомогательной поверхности (рисунки 2,а - 4,а).

Вне пределов центральной области АФР не равно нулю. Это связано не с погрешностями метода, а только с отличием формы отражателя от плоской вспомогательной поверхности. С повышением частоты центральная область отражателя уменьшается в размере, приближаясь к плоской, и модуль АФР вне центральной области стремится к нулю.

 

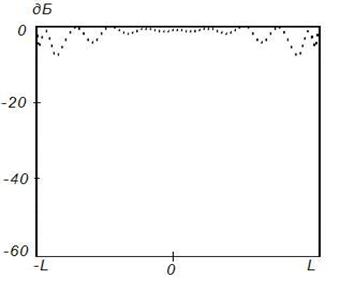
а)

     б)

       в)

Рисунок 1. Синтез ДН с заданными параметрами () на частоте , Δ=1

 

а)

            

б)

   

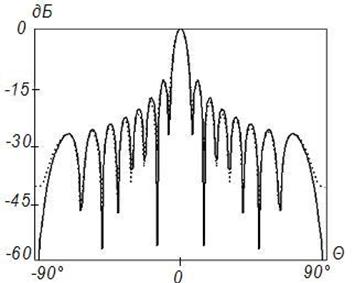
в)

Рисунок 2. Синтез ДН с заданными параметрами () на частоте 2, Δ=1

 

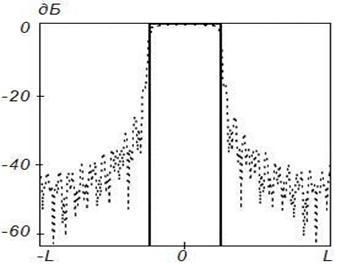
а)

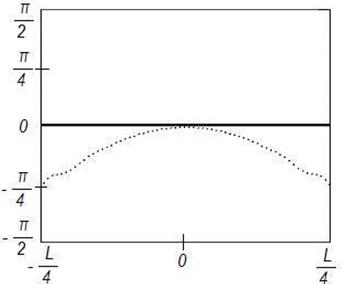
  б)

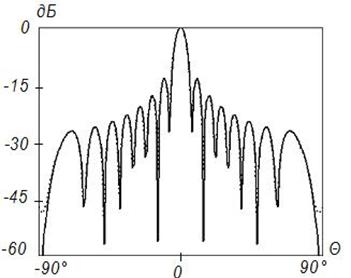
  в)

Рисунок 3. Синтез ДН с заданными параметрами () на частоте 4,  Δ=1

 

    а)

    б)

   

     в)

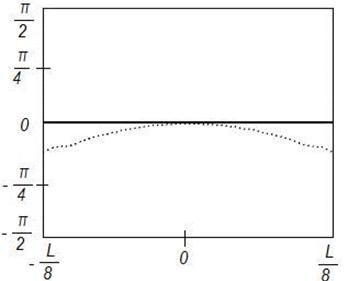
Рисунок 4. Синтез ДН с заданными параметрами () на частоте 8, Δ=1

 

  

     а)

       б)

        

        в)

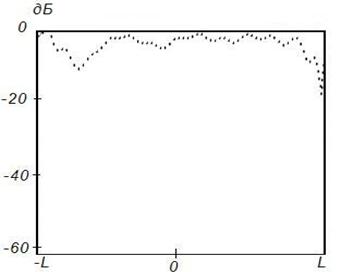
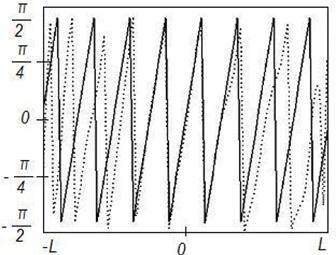
Рисунок 5. Синтез ДН с заданными параметрами () на частоте , Δ=1

   а)

     б)

    

      в)

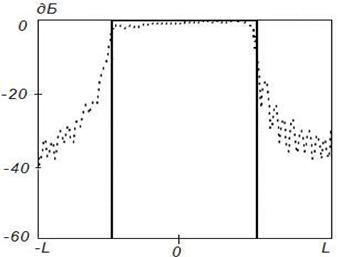
Рисунок 6. Синтез ДН с заданными параметрами () на частоте 2, Δ=1

    а)

    б)

   

        в)

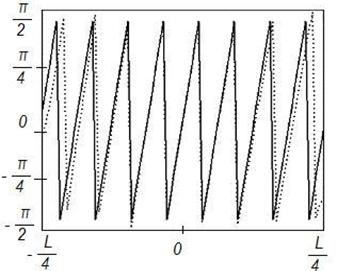
Рисунок 7. Синтез ДН с заданными параметрами () на частоте 4, Δ=1

      а)

    б)

     

        в)

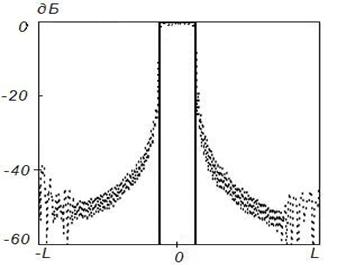
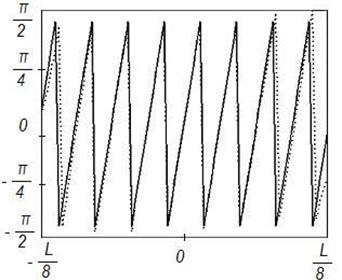
Рисунок 8. Синтез ДН с заданными параметрами () на частоте 8, Δ=1

 

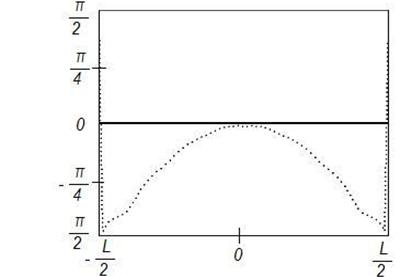
Аналогичное объяснение имеет и отличие фазового распределения токов на поверхности отражателя от заданного фазового распределения токов (рис. 1,б, 2,б, 3,б, 4б). При повышении частоты центральная область отражателя сокращается  в размере,  приближаясь  к плоской,  и  распределение  токов  по

центральной области отражателя приближается к синфазному. На рисунках 5-8 представлены результаты синтеза АФР на поверхности отражателя для случая отклоненного луча  при постоянном амплитудном распределении на вспомогательной поверхности. Как следует из результатов расчета, на частоте  наблюдается некоторое различие поведения амплитуды токов в заданном и синтезированном распределениях. Однако, как и в случае неотклоненного луча, с ростом частоты в пределах центральной области отражателя, равной по размерам вспомогательной поверхности, это различие уменьшается. Отличие синтезированного фазового распределения от линейного закона также объясняется отличием формы отражателя от плоской, которую имеет вспомогательная поверхность.

Группа рисунков 9-16 иллюстрирует применение разработанного метода синтеза для случая вспомогательной ДН, сформированной с использованием спадающего распределения вида (11) на вспомогательной поверхности при . При этом приведенные на рисунках 9-12 результаты соответствуют случаю ориентации главного максимума заданной ДН , приведенные на рисунках 13-16 ‑ случаю .

        

а)

б)

     

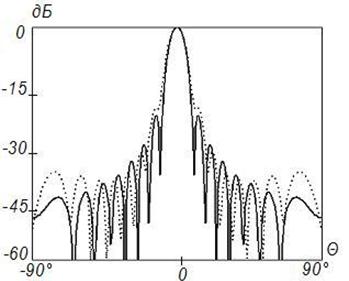
     в)

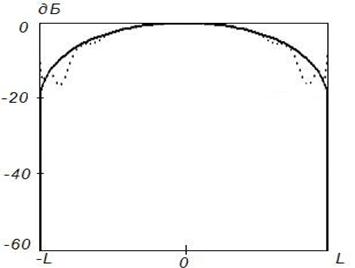
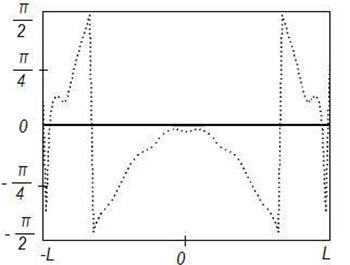
Рисунок 9. Синтез ДН с заданными параметрами () на частоте ,   Δ=0,1

 

          

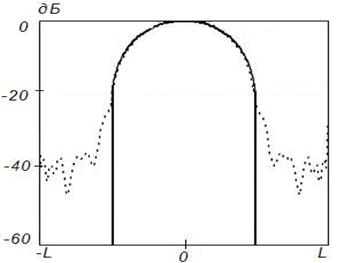
а)

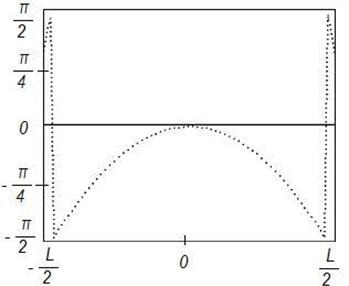
б)

     

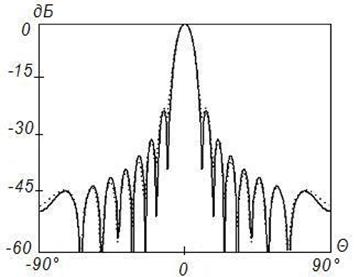
в)

Рисунок 10. Синтез ДН с заданными параметрами () на частоте 2, Δ=0,1

а)

  б)

   

      в)

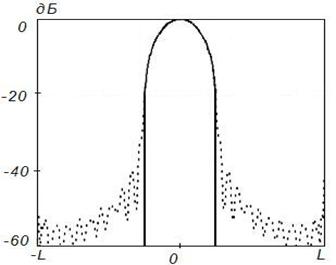
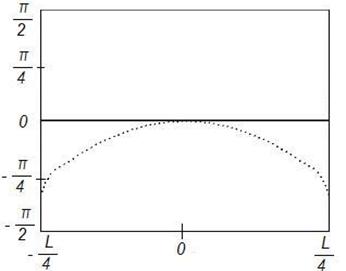
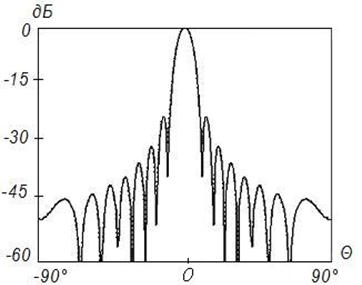
Рисунок 11. Синтез ДН с заданными параметрами () на частоте 4, Δ=0,1

     а)

 

      б)

 

         в)

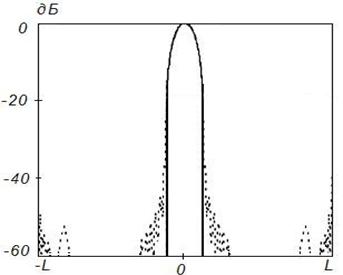
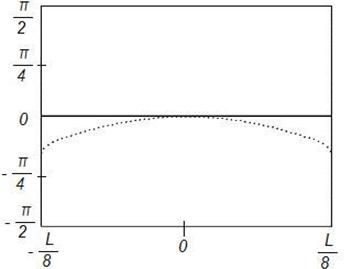
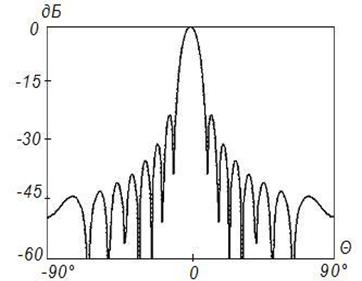
Рисунок 12. Синтез ДН с заданными параметрами () на частоте 8, Δ=0,1

 

а)

б)

        

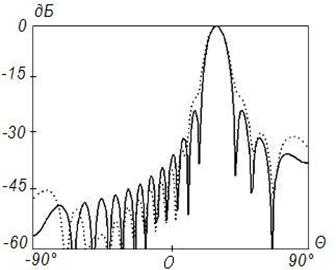
в)

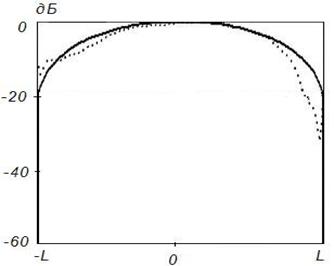
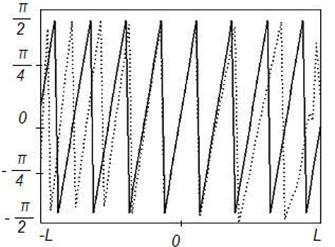
Рисунок 13. Синтез ДН с заданными параметрами () на частоте , Δ=0,1

 

 

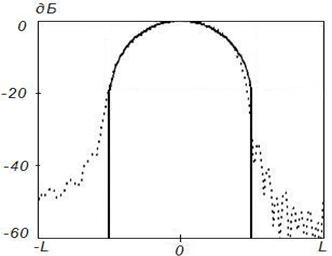
   а)

     

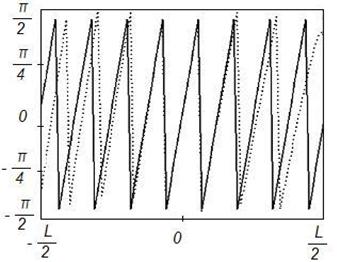
      б)

         

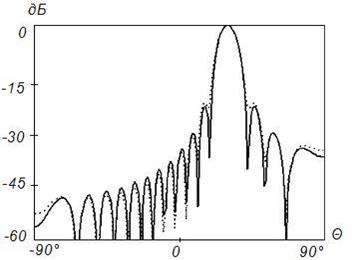
            в)

Рисунок 14. Синтез ДН с заданными параметрами () на частоте 2,  Δ=0,1

 

  а)

   б)

      

       в)

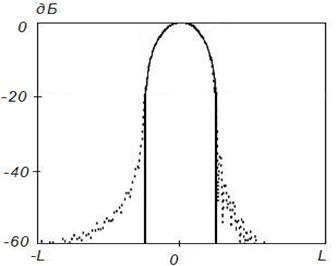
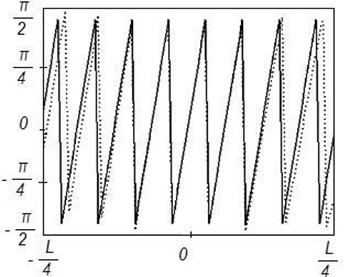
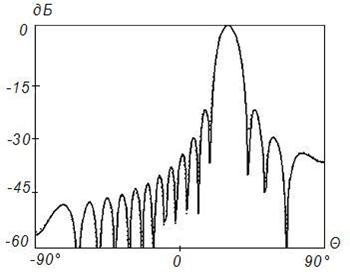
Рисунок 15. Синтез ДН с заданными параметрами () на частоте 4,  Δ=0,1

 

     а)

 

       б)

        

          в)

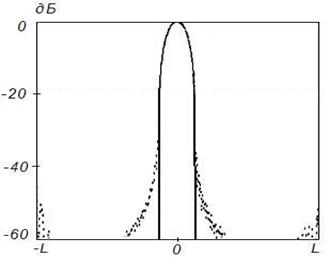
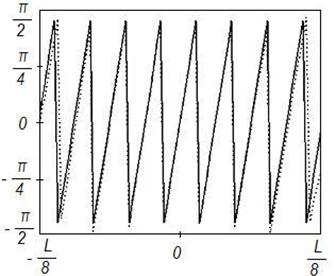
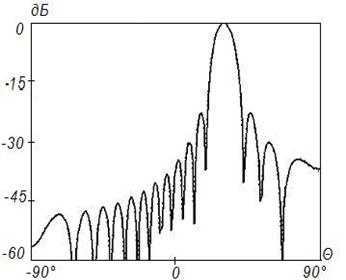
Рисунок 16. Синтез ДН с заданными параметрами () на частоте 8,  Δ=0,1

 

Данные результаты подтверждают отмеченные выше закономерности. При этом различие между заданным на вспомогательной поверхности и синтезируемым АФР меньше, чем для равномерного распределения. Уменьшение различия связано с тем, что основной вклад в формирование ДН вносят токи, возбуждаемые в центральной области отражателя, которая по своим геометрическим параметрам более близка к вспомогательной поверхности.

Более точное совпадение синтезируемого АФР с заданным для случая  спадающего распределения с физической точки зрения эквивалентно более точному совпадению амплитудно-фазовых распределений, наблюдаемому при равноамплитудном распределении  на более высоких частотах.

Таким образом, предложенный метод позволяет синтезировать частотнозависимое АФР на криволинейной поверхности, которое обеспечивает сохранение требуемых параметров ДН в широкой полосе частот.

                                                      

Литература

1. Патент 2435262 (RU) Многолучевая зеркальная антенна.- Бобков Н.И., Лизуро В.И., Шабашов А.О., Ступин В.Е., Стуров А.Г., Перунов Ю.М., Мисиков А.Ф., - Бюллетень изобретений № 33, 27.11.2011, МПК H01Q 15/14.

2. Бобков Н. И. Сверхширокополосная многолучевая зеркальная антенна. ‑ Сборник докладов международной научной конференции «ИРЭМВ-2011», Таганрог – Дивноморское, 27 июня - 2 июля  2011г., с.93-97.

3. Бобков Н. И., Габриэльян Д.Д., Зелененко А.Т., Семененко В.Н., Стуров А.Г. - Многолучевая зеркальная антенна для систем сверхширокополосной радиолокации. - Сб. докладов V Всероссийской научно-технической конференции «Радиолокация и радиосвязь», Москва, 21-25 ноября 2011 г., с.173-177.

         4. Бобков Н. И., Габриэльян Д.Д. -  Сверхширокополосная многолучевая приемная зеркальная антенна. - Сб. докладов «67-я Всероссийская конференция с международным участием «Научная сессия, посвященная Дню радио» RDC-2012, Москва, 16-17 мая 2012 г., с.14-18.

        5.  Бобков Н.И. Сверхширокополосный рупорный облучатель. – Сб. научных трудов «Современные проблемы радиоэлектроники». Материалы третьей международной конференции, Ростов-на-Дону, изд. РТИСТ ГОУ ВПО «ЮРГУЭС», 2010 г., с.248-251.

6. Бобков Н.И., Семенихин А.И., Семенихина Д.В. Рупорный облучатель для многолучевой сверхширокополосной зеркальной антенны. - Сб. докладов «67-я Всероссийская конференция с международным участием «Научная сессия, посвященная Дню радио» RDC-2012, Москва, 16-17 мая 2012 г., с.18-22.

7. Бобков Н.И., Саркисян А.А., Семенихин А.И., Семенихина Д.В. Электродинамическое моделирование рупорного облучателя многолучевой сверхширокополосной зеркальной антенны. - Сб. докладов «Радиоэлектронные средства передачи и приема сигналов и визуализации информации». Материалы второй Всероссийской конференции, г. Таганрог, 27-28 июня 2012 г., с. 18-22.

8. Бобков Н.И., Габриэльян Д.Д., Пархоменко Н.Г. Методика расчета параметров частотнозависимого покрытия отражателя сверхширокополосной многолучевой зеркальной антенны. - Сборник докладов международной научной конференции «ИРЭМВ-2013», Таганрог – Дивноморское, 24 - 28 июня  2013г., с.311-315.

       9. Басков К.М., Бобков Н.И., Краснолобов И.И., Семененко В.Н. Математическое моделирование сверхширокополосной многолучевой зеркальной антенны. // Журнал радиоэлектроники: электронный журнал. 2013. №4. URL: http: // jre. cplire.ru/ jre/apr13/9/text.pdf (дата обращения 25.07.2013 г.).

10. Фролов О.П., Вальд В.П. Зеркальные антенны для земных станций спутниковой связи. – М.: Горячая линия-Телеком, 2008. – 496 с.

11. Будагян И.Ф., Щучкин Г.Г. Моделирование характеристик излучения зеркальных антенн с корректирующим переменным импедансом // Антенны. 2004. №12 (91)., с.6-27.

12. Зелкин Е.Г., Кравченко В.Ф. Задачи синтеза антенн и методы их решения. Кн.1. – М.: ИПРЖР, 2002. – 72 с.: ил.

13. Зелкин Е.Г., Кравченко В.Ф. Синтез антенн на основе атомарных функций. Кн.2. – М.: ИПРЖР, 2003. – 72 с.: ил.

14. Бахрах Л.Д., Кременецкий С.Д. Синтез излучающих систем. Теория и методы расчета. – М.: Сов. радио, 1974.

15. Васильев, Е.Н. Возбуждение тел вращения / Е.Н. Васильев.  ‑ М.: Радио и связь, 1987. ‑ 272 с.

16. Габриэльян Д. Д., Звездина М.Ю., Цыпорина И.Г., Шацкий В.В., Шацкий Н.В. Формирование диаграммы направленности плоской активной фазированной решетки с произвольной границей раскрыва // Журнал радиоэлектроники: электронный журнал. 2012. №12. URL: http: // jre. cplire.ru/ jre/dec12/1/text.pdf (дата обращения 10.01.2013 г.).

17. Устройства СВЧ и антенны. Проектирование фазированных антенных решеток: Учеб. пособие для вузов / Д.И. Воскресенский, В.И. Степаненко, В.С. Филиппов и др. Под ред. Д.И. Воскресенского. 3-е изд., доп. и перераб. – М.: Радиотехника, 2003. – 632 с.

18. Волошин В.А., Ларин А.Ю., Оводов О.В. Алгоритм синтеза линейных антенных решеток по заданной огибающей боковых лепестков диаграммы направленности // Антенны. 2011. №12(175)., с.3-8.

19. Гантмахер Ф.Р. Теория матриц. 4-изд. М.: Наука. Гл. ред. физ.-мат. лит. 1988.