| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 12 , 2000 |
ВЛИЯНИЕ
НЕОДНОРОДНОСТИ СРЕДЫ В ПЛОСКОМ ВОЛНОВОДЕ НА ИМПУЛЬСНОЕ ИЗЛУЧЕНИЕ ТОНКОЙ
ЭЛЕКТРИЧЕСКОЙ АНТЕННЫ
Е. А. Шорохова(1),
В. А. Яшнов(2)
(1) НИИ Измерительных Систем (НИИИС), Нижний
Новгород
(2) Нижегородский Государственный Университет
Получена 4 декабря 2000 г.
Исследовано
импульсное излучение тонкого электрического вибратора, расположенного в плоском
волноводе с идеально проводящими стенками, заполненном неоднородной средой.
Задача решена с учетом конечной проводимости
проводников антенны. Предложена модель неоднородности среды, допускающая
строгое решение краевой задачи. С использованием преобразования Фурье получены
интегральные выражения для тока в антенне и продольной (относительно оси
вибратора) компоненты напряженности электрического поля. В качестве примера
проведены расчеты отклика антенны на приложенное к ней импульсное напряжение
колоколообразной формы. Проанализировано влияние неоднородности среды в
волноводе на характеристики электрической антенны.
ВВЕДЕНИЕ
Теоретические и экспериментальные исследования особенностей излучения и распространения импульсных сигналов в различных средах представляют значительный интерес для радиолокации с целью подповерхностного зондирования земных недр [1-3], для радиосвязи с подземными и подводными объектами [4], для диагностики среды радиофизическими методами [4]. Для этих целей в качестве передающих и приемных антенн часто используют электрические вибраторы. В связи с широким применением в современной радиолокации широкополосных и сверхширокополосных сигналов становятся актуальными исследования рассеивающих свойств вибраторных антенн при действии негармонических сигналов [5].
При расчетах характеристик вибраторных антенн широко используется модель тонкой цилиндрической антенны. Отклик проволочной антенны при ее импульсном возбуждении обычно рассчитывают методом преобразования Фурье [5-8]. В работе [9] для исследования переходных процессов в тонких проволочных антеннах применяют метод, основанный на использовании свойств меморфных функций в окрестностях особых точек (Singular Expansion Method). В [10] описывается аналогичный аналитический метод, позволяющий аналитическим путем исследовать переходные процессы в симметричных вибраторах.
В работе [11] рассмотрена задача об излучении монохроматических электромагнитных волн тонким идеально проводящим электрическим вибратором, расположенным в плоском волноводе с идеально проводящими стенками, который заполнен однородным магнитодиэлектриком. Влияние омических потерь в проводниках электрической антенны на ее характеристики исследуется в [12]. В работе [13] проанализировано влияние цилиндрической магнитодиэлектрической оболочки на входной импеданс тонкого электрического вибратора в плоском волноводе. Возбуждение тонкого вибратора в плоском волноводе с однородным заполнением импульсным напряжением треугольной формы рассмотрено в [14]. Целью настоящей работы является исследование влияния неоднородности среды в плоском волноводе с идеально проводящими стенками на излучение тонкого электрического вибратора.
ИМПУЛЬСНОЕ ВОЗБУЖДЕНИЕ ТОНКОГО ЭЛЕКТРИЧЕСКОГО
ВИБРАТОРА В НЕОДНОРОДНОЙ СРЕДЕ
Рассмотрим
задачу об излучении антенны, представляющей собой электрический вибратор,
состоящий из двух тонких цилиндрических проводников с конечной
электропроводностью. Концы вибратора замкнуты на идеально проводящие стенки
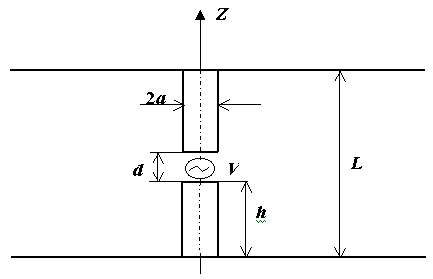
плоского волновода, как показано на Рис.
1. Здесь L - расстояние между идеально проводящими стенками волновода, ![]() - радиус проводников антенны,
- радиус проводников антенны, ![]() - длина одного из
плеч антенны, d – ширина зазора, в
котором запитывается антенна. Волновод заполнен неоднородной средой с магнитной
проницаемостью
- длина одного из
плеч антенны, d – ширина зазора, в
котором запитывается антенна. Волновод заполнен неоднородной средой с магнитной
проницаемостью ![]() и диэлектрической
проницаемостью, зависящей от расстояния до точки наблюдения r по закону
и диэлектрической
проницаемостью, зависящей от расстояния до точки наблюдения r по закону
где![]() и
и ![]() - некоторые
постоянные величины, a – радиус
цилиндрических проводников антенны. Заметим, что такая зависимость
диэлектрической проницаемости от расстояния позволяет получить строгое решение
задачи об излучении электромагнитных волн антенной, расположенной в
неоднородной среде.
- некоторые
постоянные величины, a – радиус
цилиндрических проводников антенны. Заметим, что такая зависимость
диэлектрической проницаемости от расстояния позволяет получить строгое решение
задачи об излучении электромагнитных волн антенной, расположенной в
неоднородной среде.
Рис. 1. Схематическое изображение электрического вибратора в плоском волноводе
В качестве примера рассмотрим возбуждение антенны импульсным напряжением колоколообразной формы:
где
![]() - амплитуда,
- амплитуда, ![]() - длительность импульса.
Спектр такого сигнала имеет вид
- длительность импульса.
Спектр такого сигнала имеет вид
где введено
обозначение ![]() ,
, ![]() - циклическая
частота.
- циклическая
частота.
Используя преобразование Фурье, выражение для распределения тока вдоль антенны можно представить в виде
где ток ![]() определяется через
продольную компоненту векторного потенциала с помощью соотношения
[15]
определяется через
продольную компоненту векторного потенциала с помощью соотношения
[15]
Заметим, что в силу
цилиндрической симметрии задачи электромагнитные поля не зависят от
азимутального угла и определяются только продольной к оси антенны компонентой
векторного потенциала ![]() [11], уравнение для
которой имеет вид
[11], уравнение для
которой имеет вид
где ![]() - волновое число среды,
заполняющей волновод,
- волновое число среды,
заполняющей волновод, ![]() - волновое число в вакууме,
- волновое число в вакууме, ![]() и
и ![]() - электрическая и
магнитная постоянные вакуума. Равенство нулю радиальной составляющей вектора
напряженности электрического поля на стенках волновода приводит к следующим
граничным условиям:
- электрическая и
магнитная постоянные вакуума. Равенство нулю радиальной составляющей вектора
напряженности электрического поля на стенках волновода приводит к следующим
граничным условиям:
Предположим, что на
поверхности цилиндрической антенны при ![]() выполняется граничное
условие импедансного типа
выполняется граничное
условие импедансного типа
Здесь ![]() - значение волнового
числа при
- значение волнового
числа при ![]() ;
; 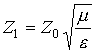 - характеристический импеданс среды, заполняющей волновод;
- характеристический импеданс среды, заполняющей волновод; 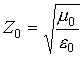 - импеданс свободного
пространства;
- импеданс свободного
пространства; ![]() - внутренний погонный
импеданс цилиндрического проводника [16]
- внутренний погонный
импеданс цилиндрического проводника [16]  , где
, где ![]() - удельная проводимость металла, из которого изготовлены
элементы антенны,
- удельная проводимость металла, из которого изготовлены
элементы антенны, ![]() и
и ![]() - функции Бесселя первого рода нулевого и первого порядка,
- функции Бесселя первого рода нулевого и первого порядка, 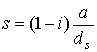 ,
, 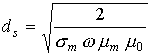 - толщина скин-слоя,
- толщина скин-слоя, ![]() - относительная
магнитная проницаемость металла. Стороннее поле в зазоре антенны считается
заданной функцией координаты и представляется в виде
- относительная
магнитная проницаемость металла. Стороннее поле в зазоре антенны считается
заданной функцией координаты и представляется в виде
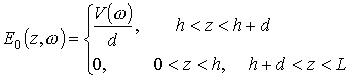
Используя тот же подход, что и в работе [11], решение краевой задачи (6)-(8) будем искать в виде ряда по собственным функциям плоского волновода. Опуская промежуточные вычисления, сразу запишем выражение для тока
где использованы следующие обозначения:
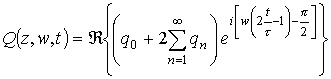 ;
; 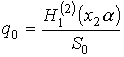 ,
, 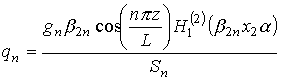 ,
,  ;
;
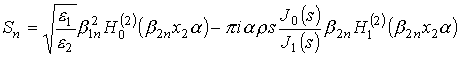 ,
,
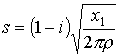 ;
;  ;
;
![]() ,
, ![]() , (c – скорость
света в вакууме).
, (c – скорость
света в вакууме).
Символ ![]() обозначает реальную
часть выражения в фигурных скобках.
обозначает реальную
часть выражения в фигурных скобках.
Аналогичным образом найдем выражение для продольной (по отношению к оси антенны) компоненты напряженности электрического поля. Применяя преобразование Фурье
а также используя решение граничной задачи для векторного потенциала и известные соотношения между потенциалами и электромагнитными полями [16], можно записать
Здесь использованы следующие обозначения:
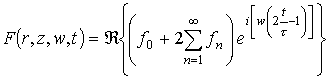 ,
,
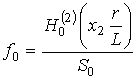 ,
,  ,
,
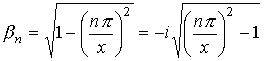 ,
, ![]() .
.
АНАЛИЗ ЧИСЛЕННЫХ РАСЧЕТОВ
Выражения (10) и
(11), полученные в
предыдущем разделе, позволяют численно проанализировать влияние неоднородности
среды в плоском волноводе на характер временных зависимостей тока и продольной
компоненты напряженности электрического поля. На
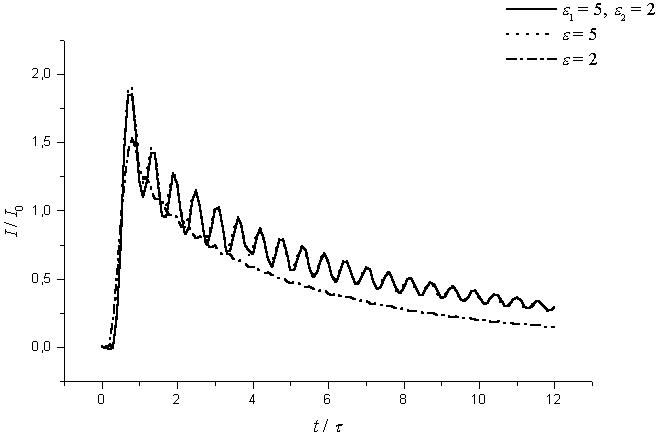
Рис.2 и Рис.3 представлены
зависимости тока, нормированного на величину 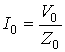 , от времени для различных значений параметра
, от времени для различных значений параметра ![]() : для длинного импульса (
: для длинного импульса (![]() ) – Рис.2 и короткого (
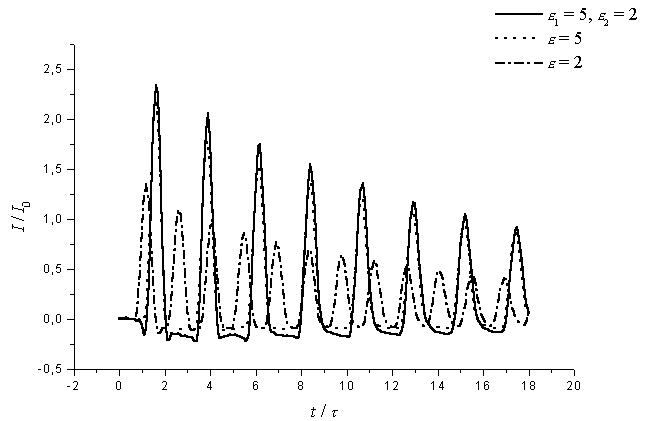
) – Рис.2 и короткого (![]() ) – Рис.3.
) – Рис.3.
Рис. 2. Временная зависимость тока для однородной и
неоднородной среды в волноводе при ![]()
Рис. 3. Временная зависимость тока для однородной и
неоднородной среды в волноводе при ![]()
Расчеты
проведены для симметричного вибратора 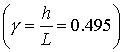 при
при ![]() ,
, ![]() ,
, ![]() и
и ![]() . Сплошная линия соответствует случаю неоднородного
заполнения волновода с
. Сплошная линия соответствует случаю неоднородного
заполнения волновода с ![]() и
и ![]() . Для сравнения там же приведены кривые для волновода,
заполненного однородной средой с
. Для сравнения там же приведены кривые для волновода,
заполненного однородной средой с ![]() (пунктирная линия) и
(пунктирная линия) и ![]() (штрих пунктирная
линия). Заметим, что такие же значения параметров и обозначения будут
использоваться и в дальнейшем. Из сравнения этих графиков видно, что в
зависимости от длительности импульса приложенной э.д.с. для неоднородного заполнения
волновода прослеживаются некоторые общие закономерности в поведение кривых: для
длинных импульсов характерно медленное спадание амплитуды тока со временем,
т.е. растягивание заднего фронта (Рис.2); с уменьшением длительности импульса в
зависимости тока от времени появляются осцилляции, амплитуда которых растет с
уменьшением длительности; для короткого импульса зависимость силы тока от
времени представляет собой последовательность импульсов, отраженных от концов
вибратора и стенок волновода (Рис.3).
(штрих пунктирная
линия). Заметим, что такие же значения параметров и обозначения будут
использоваться и в дальнейшем. Из сравнения этих графиков видно, что в
зависимости от длительности импульса приложенной э.д.с. для неоднородного заполнения
волновода прослеживаются некоторые общие закономерности в поведение кривых: для
длинных импульсов характерно медленное спадание амплитуды тока со временем,
т.е. растягивание заднего фронта (Рис.2); с уменьшением длительности импульса в
зависимости тока от времени появляются осцилляции, амплитуда которых растет с
уменьшением длительности; для короткого импульса зависимость силы тока от
времени представляет собой последовательность импульсов, отраженных от концов
вибратора и стенок волновода (Рис.3).
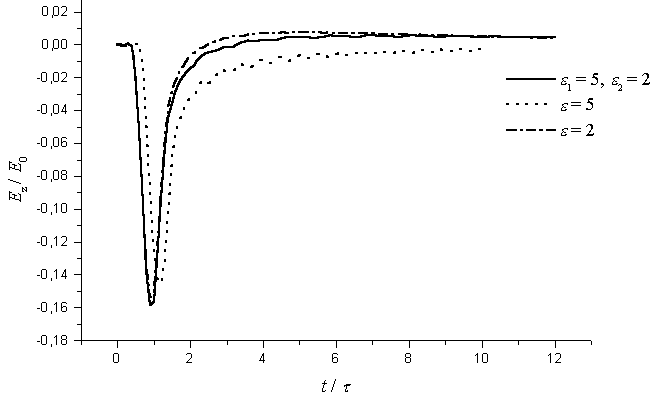
В качестве примера на
Рис.4 и Рис.5
изображены нормированные на величину ![]() временные зависимости
z-компоненты напряженности электрического поля для однородной и неоднородной
среды в волноводе, рассчитанные с помощью выражения (11). Вычисления
проводились для симметричной антенны на расстоянии от нее
временные зависимости
z-компоненты напряженности электрического поля для однородной и неоднородной
среды в волноводе, рассчитанные с помощью выражения (11). Вычисления
проводились для симметричной антенны на расстоянии от нее ![]() при двух значениях
длительности импульса (
при двух значениях
длительности импульса (![]() - Рис.4 и
- Рис.4 и ![]() - Рис.5). Из анализа
приведенных кривых видно, что наличие неоднородности среды вблизи антенны
приводит к уменьшению искажения формы излучаемого сигнала по сравнению со
случаем волновода с однородным заполнением. Наиболее ярко эта особенность
проявляется при возбуждении антенны короткими импульсами.
- Рис.5). Из анализа
приведенных кривых видно, что наличие неоднородности среды вблизи антенны
приводит к уменьшению искажения формы излучаемого сигнала по сравнению со
случаем волновода с однородным заполнением. Наиболее ярко эта особенность
проявляется при возбуждении антенны короткими импульсами.
Рис. 4. Временная зависимость z-компоненты напряженности электрического поля
для однородной и неоднородной среды в волноводе при ![]()
Рис. 5. Временная зависимость z-компоненты напряженности электрического поля
для однородной и неоднородной среды в волноводе при ![]()
ЗАКЛЮЧЕНИЕ
В представленной работе рассмотрено импульсное излучение тонкой вибраторной антенны, которая расположена в плоском волноводе с идеально проводящими стенками, заполненном неоднородной средой. С использованием преобразования Фурье получены интегральные выражения для тока и напряженности электрического поля. В качестве примера численно исследован отклик антенны на приложенное к ней импульсное напряжение колокообразной формы. При достаточно больших длительностях импульса форма излученного сигнала незначительно отличается от формы приложенной э.д.с., хотя в этом случае наблюдается затягивание заднего фронта. При возбуждении антенны короткими импульсами происходит существенное искажение подаваемого на антенну сигнала, связанное с многократным отражением волн тока от концов вибратора. Наличие неоднородности среды вблизи антенны приводит к уменьшению искажений импульсных сигналов, что особенно ярко наблюдается при возбуждении антенны короткими импульсами.
СПИСОК ЛИТЕРАТУРЫ
[1] Финкельштейн М.И., Кутаев В.А., Злотарев В.П. Применение радиолокационного подповерхностного зондирования в инженерной геологии. М.: Недра, 1986.
[2] Попов С.Б., Ярмахов И.Г. // РЭ. 2000. Т. 45. № 1. С.39.
[3] Чжань Л.Ч., Моффэтт Д.Л., Питерс Л. мл. // ТИИЭР. 1979. Т.67. №7. С.18.
[4] Хармут Х.Ф. Несинусоидальные волны в радиолокации и радиосвязи. М.: Радио и связь, 1985.
[5]
Бриккер
А.М., Зернов Н.В., Мартынова Т.Е. // РЭ. 2000. Т. 45. № 5. С.559.
[6]
Schmitt H.J., Harrison C.W., Williams C.S. // IEEE Trans. 1966. V. AP-14. № 9. P.120.
[7]
Tesche F.M. // IEEE Trans. 1974. V. AP-22.
№ 2. P.352.
[8]
Liu Y.P., Sengupta D.L. // IEEE Trans. 1974. V. AP-22. № 2. P.212.
[9]
Hoorfar A., Chang D.C. // IEEE Trans. 1982. V. AP-30. № 6. P.1145.
[10] Tesche F.M. // IEEE Trans. 1973. V. AP-21. №
1. P.53.
[11] Докучаев В.П., Яшнов В.А. // РЭ. 1996. Т. 41. № 7. С.792.
[12] Докучаев В.П., Яшнов В.А. // Радиотехника. 2000. № 4. С.28.
[13] Докучаев
В.П., Шорохова Е.А., Яшнов В.А. // IV Международная
научно-техническая конференция. Радиолокация, навигация и связь, Воронеж, 1998.
С. 1749.
[14] Docuchaev V.P., Shorochova E.A.., Yashnov V.A. // Proceedings of the XXVIII Moscow Interenational Conference on Antenna Theory and Technology, Moscow, Russia, 1998. P. 197.
[15] Марков Г.Т., Сазонов Д.М. Антенны. М.: Энергия, 1975.
[16] Вайнштейн Л.А. Электромагнитные волны. М.: Радио и связь, 1988.
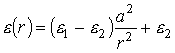 ,
,
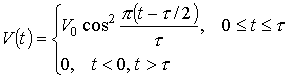 ,
,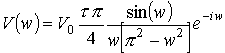 ,
,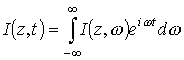 ,
, .
. 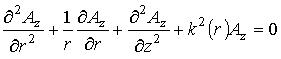 ,
, , при
, при  .
. ,
, ,
, .
.