|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 12 , 2000 | |
МНОГОТОНАЛЬНЫЙ АЛГОРИТМ ОБНАРУЖЕНИЯ РАДИОМИКРОФОНОВ
Г. В. Макаров, В. В. Быковников, А. Н. Пятунин
Воронежский Государственный технический университет
Получена 5 декабря 2000 г.
Предлагается алгоритм обнаружения радиомикрофонов, использующий многотональный тестовый сигнал, что в условиях неравномерного распределения плотности акустической энергии внутри помещения позволяет получить более высокие качественные показатели, чем при использовании однотональных сигналов. Алгоритм пригоден для использования в аппаратно-программных комплексах для поиска радиомикрофонов и технических каналов утечки информации.
Как было показано в [1], тональный алгоритм обнаружения радиомикрофонов обладает намного лучшими качественными характеристиками, чем алгоритм, использующий импульсные ЛЧМ сигналы. Но при излучении акустического тонального сигнала плотность звуковой энергии внутри помещения распределена неравномерно. Образуются области с большой энергией и области замираний. Поскольку местоположение радиомикрофона в пространстве априорно неизвестно, то существует опасность того, что он окажется в одной из областей замираний. При этом сильно ухудшится отношение сигнал/шум в канале радиомикрофона, а, следовательно, уменьшится вероятность правильного обнаружения.
Для борьбы с явлением акустических замираний предлагается использовать более сложный тестовый сигнал, состоящий из нескольких тонов разных частот. При этом области замираний для тонов разных частот будут находиться в различных точках пространства (если частоты не кратны друг другу). В этом случае вероятность того, что радиомикрофон окажется в точке замирания всех тональных сигналов, мала. Таким образом, применение многотонального тестового сигнала позволяет улучшить характеристики алгоритма. Ниже рассмотрен случай двухтонального тестового сигнала, приведен синтез алгоритма и анализ его качественных показателей.
Работа корреляционных алгоритмов
[1] основана на выявлении зависимости между тестовым акустическим колебанием a(n) и сигналом, принимаемым приемником s(n) (оба сигнала дискретизируются в аппаратуре обнаружения, n - номер временного отсчета сигнала 
). В случае обнаружения зависимости между сигналами принимается решение о наличии радиомикрофона (гипотеза H1), а в противном случае о его отсутствии (гипотеза H0).
Предполагается, что мешающий сигнал представлен в виде нормального гауссовского шума. При справедливой гипотезе H0 входной сигнал представляет собой чисто шумовую последовательность
,
где 
- отсчеты шумового сигнала. При справедливой гипотезе H1 сигнал на входе обнаружителя представляет собой аддитивную смесь детерминированного тестового сигнала a(n) и шума
,
где k – масштабный коэффициент, определяемый усилительными свойствами радиомикрофона, 
- отсчеты шумового сигнала.
Для двухтонального тестового сигнала акустическое колебание a(n) представляет собой сумму двух гармонических функций
,
,
где 
,
- приращения фазы, 
,
- неизвестные начальные фазы
,
,
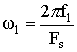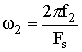где f1, f2- частоты гармонических колебаний, FS - частота дискретизации.
В первом приближении выборки 
и 
можно принять за совокупность некоррелированных гауссовских величин неизвестной интенсивности. Обозначим средние мощности шума величинами 
и 
соответственно.
Синтез алгоритмов обнаружения детерминированных сигналов неизвестной интенсивности на фоне нормального белого шума описан в [2]. Аналогично можно синтезировать алгоритм для обнаружения многотональных сигналов.
Учитывая взаимную независимость отсчетов сигнала s(n), их совместная плотность распределения вероятностей равна произведению распределений каждого отсчета, тогда функционалы правдоподобия для гипотез H0, H1 будут иметь вид
,
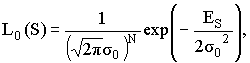
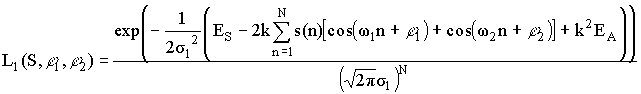где ES – энергия сигнала s(n),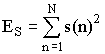 
,
EА – энергия акустического сигнала a(n), 
.
В функционал 
входят неизвестные параметры 
. Чтобы избавиться от этой зависимости, необходимо провести усреднение по .
Воспользуемся подстановкой
,
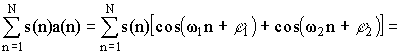
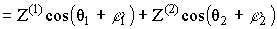где
,
,
,
,
,
,
,
,
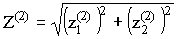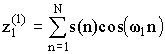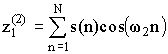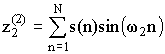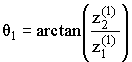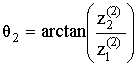тогда нетрудно показать что
,
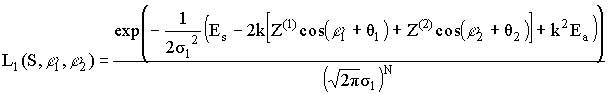Усредняя функционал правдоподобия 
по 
получим
,
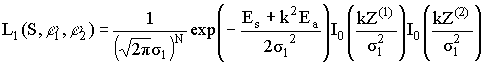где I0(x) – функция Бесселя чисто мнимого аргумента первого рода нулевого порядка.
Полагая, что отношение сигнал/шум на выходе корреляторов огибающей велико
,
,
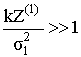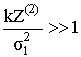можно записать
,
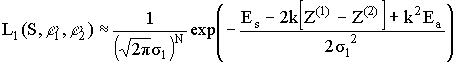Задачу обнаружения будем решать методом максимума правдоподобия. В нашем случае неизвестными являются параметры 
, 
и масштабный коэффициент k. Найдем максимально правдоподобные оценки величин 
и 
,
.
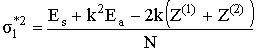После замены неизвестных значений параметров и их максимально правдоподобными оценками и выполнения ряда простых преобразований отношение функционалов правдоподобия примет вид
.
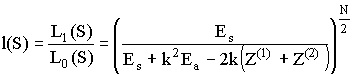Максимально правдоподобная оценка величины k равна
.
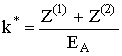Подставляя вместо неизвестной величины k в отношение функционалов правдоподобия ее максимально правдоподобную оценку и проведя ряд несложных преобразований, получим
.
Отсюда выразим оптимальное правило принятия решения о наличии радиомикрофона
.
Преобразуем неравенство в следующий вид
.
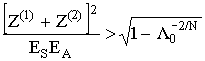Правая часть этого неравенства является константой
,
а оптимальное правило принятия решения принимает вид
.
где Z(N) – сумма корреляций огибающих входных гармонических колебаний
.
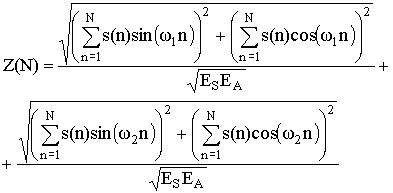Мы получили оптимальное правило принятия решения для двухтонального алгоритма. Для оценки качества обнаружения в условиях замираний акустического сигнала следует воспользоваться приближенной акустической моделью помещения и исследовать качественные показатели алгоритма методом статистического моделирования. Такую модель можно построить на основе геометрической или волновой теории акустики [3].
Для построения модели помещения воспользуемся геометрической теорией акустики. В [3] приведен ряд формул, позволяющих рассчитать энергию и задержку прихода лучей от любого мнимого источника звука в предположении, что микрофон и действительный источник звука расположены в любых произвольных точках пространства. Это довольно сложные формулы с множеством степеней свободы. В нашем случае мы можем зафиксировать расположение источника тестового сигнала в любой конкретной точке, например, в геометрическом центре помещения. И если ввести декартову систему координат с началом в геометрическом центре помещения, то формула для вычисления расстояния d между микрофоном и мнимым источником звука упростится и примет вид
,
где l, m, n - индексы мнимых источников звука 
(случай, когда l=m=n=0 - соответствует действительному источнику звука),
x, y, z - координаты микрофона,
X, Y, Z - линейные размеры помещения.
При каждом отражении энергия акустического сигнала уменьшается в 
раз, где 
- коэффициент звукового поглощения поверхностей. Таким образом, колебание, воздействующее на микрофон, примет вид
,
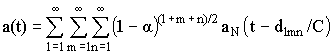где aN (t) - сигнал источника звука,
C - скорость распространения звука в воздухе.
Коэффициент поглощения можно приближенно рассчитать исходя из времени реверберации по формуле Сэбина [3,4]
,
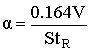где V - объем помещения,
S - площадь поверхностей помещения,
tR - время реверберации.
Данная модель верна в предположении, что микрофон и источник звука ненаправленные, а помещение совершенно пустое с формой параллелепипеда и все его поверхности имеют одинаковый коэффициент поглощения. Также не учитываются потери при распространении звука в воздухе, которые для частот менее 4000 Гц пренебрежительно малы. Конечно, такая модель не претендует на полноту описания акустической картины, но она позволяет качественно оценить влияние акустических искажений на форму принимаемого сигнала.
При излучении гармонического колебания, зная задержку прихода и коэффициент поглощения для каждого луча можно найти соотношение между амплитудами и фазами излученного и принятого сигнала. Если колебания накладываются друг на друга, то результат определяется как сумма синусоидальных величин [5]. В случае если колебания имеют одинаковую частоту, то их сумма имеет ту же частоту
,
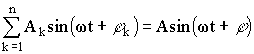где Ak, 
- амплитуда и фаза k-го колебания.
При n=2 имеют место следующие соотношения:
,
,
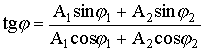На основе этих формул можно рассчитать амплитуду и фазу гармонического сигнала в любой точке помещения.
Проведем статистическую оценку качества обнаружения для однотонального и двухтонального алгоритмов. Наиболее наглядной является оценка качества с помощью кривых обнаружения, которые отображают зависимость между отношением сигнал/шум 
и вероятностью правильного обнаружения D. Для лучшей наглядности мы будем использовать отношение сигнал/шум по мощности в логарифмическом масштабе , выраженное в дБ (отношение мощности излученного акустического сигнала к уровню шума, приведенному к входу обнаружителя). Для моделирования акустических свойств помещения воспользуемся описанной моделью. В качестве параметров модели выберем линейные размеры помещения равные 4x6x10 м, время реверберации 0.5с и стандартную частоту дискретизации 8000 Гц.
На рис.1 изображены кривые обнаружения для однотонального алгоритма. В качестве тестового использован гармонический сигнал длительностью 128 отсчетов. Каждая кривая построена по 11 точкам. Каждая точка является результатам проведения 100000 опытов. Для построения графика между точками используется сплайновая аппроксимация. На каждом рисунке изображено по четыре кривые, соответствующие разным значениям вероятности ложной тревоги F=10-1, 10-2, 10-3, 10-4 и соответствующие значения пороговых уровней l1, l2, l3, l4. Как показано в [4], границе разборчивости речи соответствует уровень –5 дБ. А так как мы имеем дело с закрытым помещением, уровень речевых сигналов возрастает приблизительно на 6-7 дБ по сравнению с открытым пространством. Таким образом, качество алгоритмов следует оценивать при соотношении сигнал/шум в районе –15 дБ и выше.
Рис.1. Кривые обнаружения для однотонального алгоритма
На рис. 2 изображены кривые обнаружения для двухтонального алгоритма при той же длительности тестового сигнала и тех же исходных данных.
Рис.2. Кривые обнаружения для двухтонального алгоритма
Как видно из графиков, в условиях акустических замираний применение двухтонального алгоритма позволяет улучшить качественные показателями обнаружения сравнению с однотональным алгоритмом. Например, при отношении сигнал/шум –15 дБ и вероятности ложной тревоги 10-3, двухтональный алгоритм обеспечивает вероятность правильного обнаружения около 0.88, в то время как однотональный алгоритм около 0.8. Таким образом, изменение формы сигнала позволяет улучшить характеристики алгоритма. Описанный алгоритм был внедрен в производство и использован в программно-аппаратном комплексе поиска каналов утечки информации АРК-Д1Т, выпускаемым фирмой ЗАО “ИРКОС” (www.ircoc.ru).
ЛИТЕРАТУРА
Авторы:
Профессор Макаров Геннадий Васильевич
Быковников Владимир Владимирович, е-mail: vb@ircoc.vrn.ru
Пятунин Андрей Николаевич
Воронежский Государственный технический университет
 |
 |
