УДК 537.876.4
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ РАСПРЕДЕЛЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ В
ВОЛНОВОДЕ НА ОСНОВЕ ФОТОННОГО КРИСТАЛЛА
А. С. Логгинов,
А. Ш. Майоров
Московский государственный университет им. М. В. Ломоносова, физический
факультет
Получена 19 апреля 2006 г.
Методом
численного моделирования рассчитаны распределения электромагнитных полей в
волноводе на основе фотонного кристалла. Двумерное уравнение Даламбера,
описывающее процесс распространения волны в интегрально-оптическом устройстве,
решено методом конечных разностей с помощью явной численной схемы типа "крест". Показано, что волновод на основе фотонного кристалла
обладает частотной селективностью. Это явление может найти применение при создании
высокоскоростных систем связи со спектральным уплотнением каналов. Волноводы на
основе фотонных кристаллов могут быть использованы в качестве базовых элементов
нового поколения интегрально-оптических схем.
Введение
Стремительное
развитие технологии изготовления устройств интегральной оптики и увеличение
производительности персональных компьютеров открывают возможности для
численного моделирования и экспериментальной реализации приборов, использующих
фотонные кристаллы (ФК) [1]. ФК называют строго периодичную структуру, период
которой сравним с длиной волны падающего на нее оптического излучения. При
взаимодействии света с ФК возникает ряд кардинально новых явлений.
Многократная
интерференция электромагнитных волн, дифрагировавших на каждой элементарной
ячейке кристалла, приводит к образованию диапазонов частот (фотонных
запрещенных зон), для которых распространение излучения по ФК невозможно. На
этих частотах свет испытывает идеальное отражение от поверхности кристалла
вследствие деструктивной интерференции, в то время как на других частотах он
проходит через ФК. Это явление может быть использовано для решения широкого
спектра физических задач, связанных с локализацией и эмиссией света. Материалы
с фотонными запрещенными зонами позволяют создавать лазеры с микрорезонаторами,
высокоэффективные волноводы, высокоскоростные оптические переключатели [2]. ФК
обладают и многими другими интересными свойствами, связанными с дисперсией,
оптической анизотропией и поляризационными характеристиками излучения. Такие
свойства открывают возможность создания эффективных дисперсионных
компенсаторов, преобразователей частоты, современных суперпризм, оптических
поляризаторов, фильтров и т. д. [3–5]
Целью настоящей
работы является численное моделирование распространения электромагнитной волны
и расчет характеристик волновода на основе фотонного кристалла (рис.1). В нем
создан волноведущий канал, ширина которого равна  . Основная задача исследования —
изучение селективности подобного устройства. ФК, период которого обозначим
символом
. Основная задача исследования —
изучение селективности подобного устройства. ФК, период которого обозначим
символом  ,
образован элементарными ячейками в форме квадрата со стороной
,
образован элементарными ячейками в форме квадрата со стороной 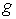 .
.
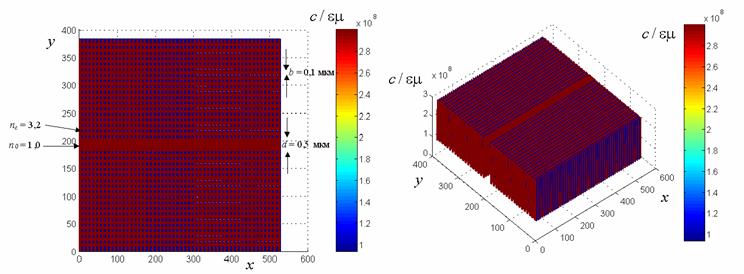
Рис. 1, 2. Волновод на основе ФК.
Методы
Для определения
характеристик изучаемого волновода для случая 
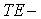 распространения ограничимся
рассмотрением только одной компоненты поля —
распространения ограничимся
рассмотрением только одной компоненты поля —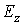 , для которой справедливо
скалярное уравнение Даламбера [6]:
, для которой справедливо
скалярное уравнение Даламбера [6]:
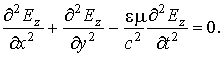 (1)
(1)
В работах [7] и [8], посвященных
численному моделированию интегрально-оптических устройств, при вычислениях
рассматривают уравнения Максвелла и для их решения используют алгоритм Кейна Йе.
Непосредственное сравнение этой методики с результатами численного решения
уравнения (1) показало, что его использование позволяет сократить время
вычислений примерно на порядок. Этот выбор весьма важен, так как в
рассматриваемой задаче объем вычислений значителен.
Явная численная
схема типа "крест" [9] для двумерного волнового уравнения (1)
может быть изображена в виде шаблона (рис.3). Сделаем некоторые пояснения.
Пространство и компонента напряженности электрического поля 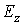 дискретизированы
так, что пространственная точка представлена как
дискретизированы
так, что пространственная точка представлена как 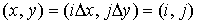 , а
, а 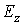 —
— 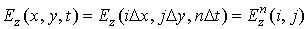 , где
, где  ,
, 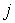 и
и 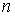 — целые числа,
— целые числа, 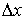 и
и 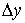 —
пространственные приращения,
—
пространственные приращения,  — временное
приращение. Пространственные и временные производные второго порядка в (1)
заменяются так:
— временное
приращение. Пространственные и временные производные второго порядка в (1)
заменяются так:
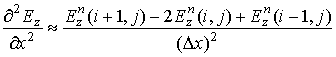 , (2)
, (2)
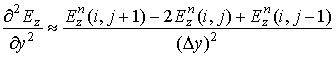 , (3)
, (3)
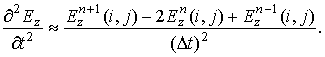 (4)
(4)
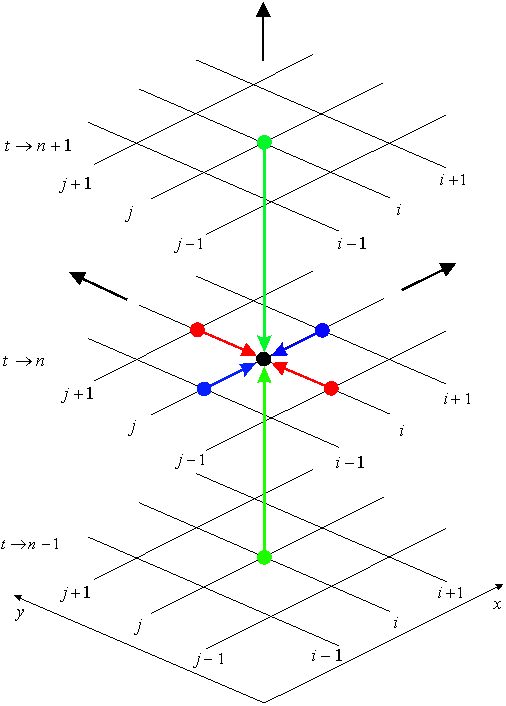
Рис. 3. Шаблон для явной
трехслойной численной схемы типа “крест”.
Если производные вычислять таким образом, тогда
погрешность аппроксимации численной схемы порядка 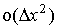 ,
,  и
и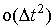 . Если учесть (2)–(4), то
конечно-разностная форма (1) примет вид:
. Если учесть (2)–(4), то
конечно-разностная форма (1) примет вид:
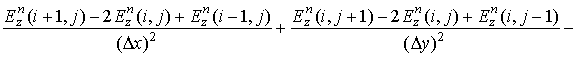
(5)
 .
.
Используя (5),
найдем решение на 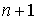 шаге по времени. Оно вычисляется по
(6), для этого необходимо знать распределение
шаге по времени. Оно вычисляется по
(6), для этого необходимо знать распределение 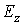 в двух предыдущих шагах времени.
в двух предыдущих шагах времени.
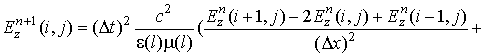
(6)
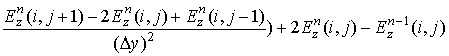 ,
,
где 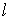 характеризует
точку пространства, соответствующую текущим значениям
характеризует
точку пространства, соответствующую текущим значениям 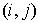 , с диэлектрической
проницаемостью
, с диэлектрической
проницаемостью 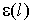 и магнитной проницаемостью
и магнитной проницаемостью  , а
, а 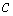 — скорость
света в вакууме.
— скорость
света в вакууме.
Существуют определенные практические соображения при дискретизации
пространства координат. Для того чтобы длина волны была представлена корректно,
пространственные интервалы должны быть малы по сравнению с ней. При выборе
временного шага дискретизации необходимо учитывать обобщенное условие
устойчивости Куранта [9]:
 (7)
(7)
Уравнение (6) необходимо дополнить граничными и начальными условиями. В
задаче анализа электромагнитных полей в волноводе на основе ФК исследуемое
пространство содержит поля, уходящие в бесконечность. Поскольку вычисления
можно производить лишь в конечной области, рассматриваемое пространство
необходимо ограничить, и на этих границах волны должны быть поглощены без
возникновения существенных отражений [8].
Выбором начальных условий в систему
вводится входной сигнал (гауссов профиль по оси 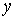 , модулированный гармонической
функцией с несущей частотой оптического сигнала). Математический образ входного
сигнала можно представить в виде (8):
, модулированный гармонической
функцией с несущей частотой оптического сигнала). Математический образ входного
сигнала можно представить в виде (8):
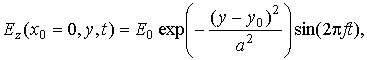 (8)
(8)
где  - амплитуда входного сигнала,
- амплитуда входного сигнала, 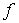 — несущая частота, значения
— несущая частота, значения 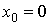 ,
, 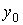 и
и 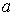 задают форму и
пространственное положение функции Гаусса.
задают форму и
пространственное положение функции Гаусса.
Результаты
Численное моделирование двумерного волнового уравнения
(1) выполнено с использованием явной трехслойной схемы типа "крест" [9]. При расчете предполагались следующие
параметры системы (рис.1, 2): показатель преломления материала ФК 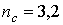 ; показатель
преломления окружающей среды
; показатель
преломления окружающей среды 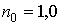 ; ширина волноведущего канала
; ширина волноведущего канала 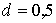 мкм; период ФК
мкм; период ФК
 мкм,
размер элементарной ячейки
мкм,
размер элементарной ячейки 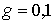 мкм. На рис. 4–11 показано распределение компоненты электромагнитного
поля
мкм. На рис. 4–11 показано распределение компоненты электромагнитного
поля 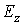 в
устройстве (рис.1, ) при возбуждении волновода сигналом (8) различной несущей
длины волны. ФК при определенных значениях длины волны
в
устройстве (рис.1, ) при возбуждении волновода сигналом (8) различной несущей
длины волны. ФК при определенных значениях длины волны 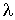 является "зеркалами", обеспечивающими волноводный режим распространения
света, отражающегося от них.
является "зеркалами", обеспечивающими волноводный режим распространения
света, отражающегося от них. 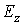 при
волноводном распространении содержит "боковые лепестки", образующиеся при
интерференции света. Рис.4-12
демонстрируют спектральную селективность волновода на основе ФК. Это явление
может найти применение при создании высокоскоростных систем связи со
спектральным уплотнением каналов (WDM).
при
волноводном распространении содержит "боковые лепестки", образующиеся при
интерференции света. Рис.4-12
демонстрируют спектральную селективность волновода на основе ФК. Это явление
может найти применение при создании высокоскоростных систем связи со
спектральным уплотнением каналов (WDM).
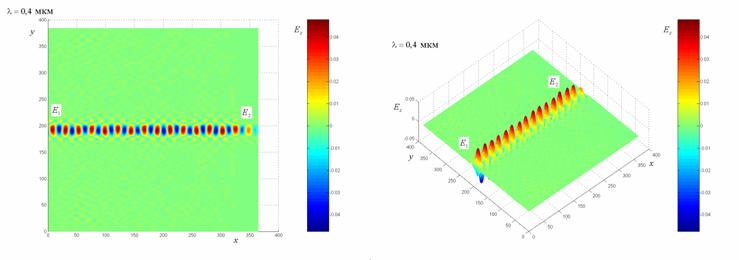
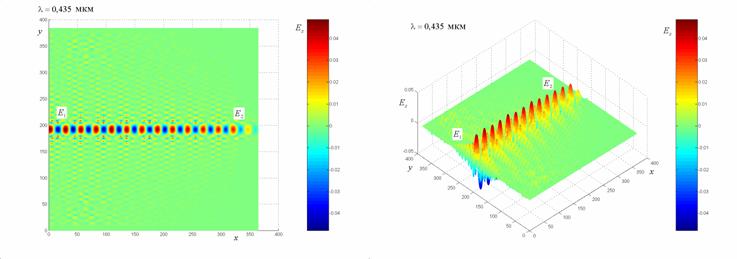
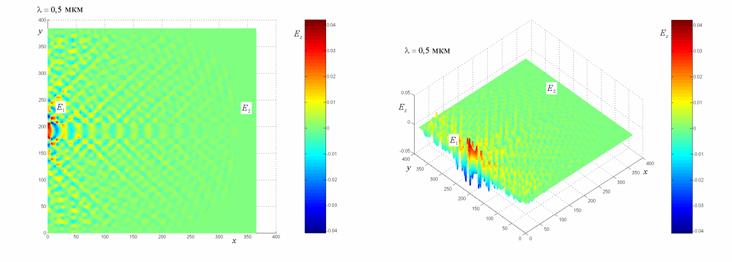

Рис. 4–11. Распределение компоненты электромагнитного поля 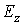 в волноводе
при распространении по нему электромагнитной волны с различной несущей
частотой.
в волноводе
при распространении по нему электромагнитной волны с различной несущей
частотой.

Рис. 12. Зависимость отношения амплитуды
электромагнитного поля на выходе волновода на основе ФК к амплитуде на входе от
длины волны входного сигнала.
Заключение
Численное
моделирование позволяет определить распределение компоненты электромагнитного
поля 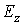 для
предложенной конфигурации волновода на основе фотонного кристалла. Эти
результаты являются основополагающими при проектировании (выборе требуемых
параметров) и дальнейшей реализации устройств интегральной оптики. Компактность,
высокое быстродействие и возможность интеграции ФК волноводов с ФК направленными
ответвителями и резонаторами на одной подложке позволит использовать эти
устройства в новом поколении интегральных схем.
для
предложенной конфигурации волновода на основе фотонного кристалла. Эти
результаты являются основополагающими при проектировании (выборе требуемых
параметров) и дальнейшей реализации устройств интегральной оптики. Компактность,
высокое быстродействие и возможность интеграции ФК волноводов с ФК направленными
ответвителями и резонаторами на одной подложке позволит использовать эти
устройства в новом поколении интегральных схем.
Литература
[1] Joannopoulos J.D., Meade R.D., Winn J.N. Photonic Crystals: Molding the Flow of Light, Princeton: Princeton University Press,
1995. Pp. 45–50.
[2] Baba T. // IEEE J. Select. Topics Quantum Electron. 1997. Vol.
3. № 3. Pp. 808–830.
[3] Kosaka H., Kawashima T., Tomita A. et al. // J. Lightwave Technol.
1999. Vol. 17. № 11. Pp. 2032–2038.
[4] Steeland M.J., Osgood R.M. // J. Lightwave Technol. 2001. Vol.
19. № 4. Pp. 495–503.
[5] Imada M., Noda S., Chutinan A. et al // J. Lightwave Technol.
2002. Vol. 20. № 5. Pp. 873–878.
[6] Логгинов
А.С., Майоров А.Ш., Кряжимский С.А. // Радиотехника. 2005. №1.
Cтр. 24–29.
[7] Hagness S.C., Rafizadeh D., Ho S. T., and Taflove A. // J. Lightwave
Technol. 1997. Vol. 15. № 11. Pp. 2154–2165.
[8] Chu S.T. and Chaudhuri
S.K. // J. Lightwave Technol. 1989. Vol. 7. № 12. Pp. 2033–2038.
[9] Калиткин
Н.Н. Численные методы. М.: Наука, 1978. 425–439 с.
. Основная задача исследования — изучение селективности подобного устройства. ФК, период которого обозначим символом
, образован элементарными ячейками в форме квадрата со стороной
.

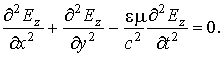
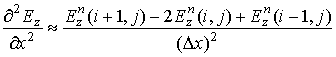 , (2)
, (2)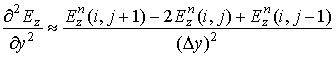 , (3)
, (3)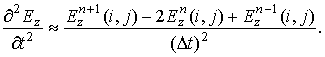 (4)
(4)
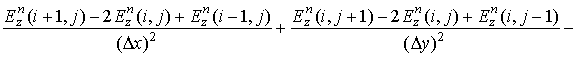
 .
. 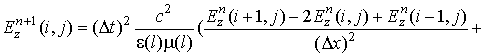
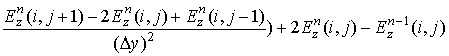 ,
, 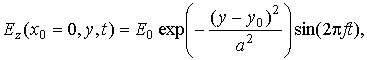 (8)
(8)



