Стенка радиопрозрачного укрытия, состоящая из диэлектрических слоев и компенсационных металлических решеток
К. М. Басков
Институт теоретической и прикладной электродинамики РАН
Получена 8 декабря 2011 г.
Аннотация. Исследуются новые возможности применения компенсационных металлических решеток при создании радиопрозрачных укрытий, предназначенных для защиты объектов, работающих в дециметровом и длинноволновой части сантиметрового диапазонов длин волн. Рассматривается использование искривленных проводов в компенсационных решетках, за счет чего увеличивается эквивалентное реактивное поверхностное сопротивление решетки. В результате можно оптимальным образом производить электродинамическое согласование тонкой диэлектрической стенки радиопрозрачного укрытия в дециметровом и длинноволновой части сантиметрового диапазонов длин волн.
Ключевые слова: радиопрозрачное укрытие, компенсационные решетки, эквивалентная линия передачи, слоистый диэлектрик.
Abstract. We investigate new possibilities of countervailing metal grids to create radio-shelters for the protection of facilities, work-melting in the decimeter and centimeter wavelength ranges of wavelengths. Be regarded a case of twisted wires in the compensation grids, thereby increasing the surface resistance of the equivalent reactance of the lattice. This allows an optimal way to produce electrodynamic matching thin dielectric wall radome in the decimeter and centimeter wavelength ranges of wavelengths.
Keywords: radome, compensating lattice, equivalent long line, sandwich dielectrics structure.
Введение
При создании радиопрозрачных укрытий (РПУ) с улучшенными радиотехническими характеристиками часто используют конструкцию стенки с включением металлических решеток индуктивного типа [1] (рис. 1). Это позволяет решать различные конструкционные задачи, такие как повышение радиопрозрачности стенки, увеличение ее прочности, обеспечение подогрева для защиты от снега и наледи, обеспечение освещения внутри укрытия.

Рис.1. Решетка из металлических полосок (проводов) шириной t с периодом Tx.
В последнее время публикуется много патентов, в которых приводятся конструкции стенок с решетками с индуктивной проводимостью (например, [2,3,4]), что свидетельствует о перспективности такого способа повышения качества РПУ.
Часто для защиты РПУ от обледенения, статического электричества (молниезащита), а также для обеспечения освещения используется решетка из проводов, индуктивная проводимость которой частично компенсируется решеткой из вибраторов, обладающей емкостным характером отражения падающей волны [2]. Однако внесение дополнительных элементов с емкостным характером отражения может оказаться малоэффективным и привести к сужению диапазона частот и углов падения волны, в котором стенка укрытия обладает низким уровнем отражения.
Известна стенка РПУ для антенн прицельных станций и систем сопровождения целей [3], состоящая из диэлектрических слоев и металлических элементов в виде решёток с индуктивной проводимостью из набора периодически расположенных металлических проводов. Такая стенка может быть использована для создания РПУ изделий, работающих в миллиметровом диапазоне и верхней части сантиметрового диапазона длин волн.
В работе [4] описана стенка РПУ для СВЧ датчиков в автомобиле, которая состоит из диэлектрического слоя, толщина которого кратна половине длины падающей волны. Слой лакокрасочного покрытия, который необходимо наносить на стенку РПУ, ухудшает прохождение радиоволн через стенку. Для компенсации влияния лакокрасочного покрытия в этой работе предлагается использовать решетку из проводов, параллельных вектору напряженности электрического поля, излучаемого укрываемым датчиком. Так как СВЧ датчики в автомобилях, как указано в этой публикации, работают в миллиметровом диапазоне длин волн, такой способ компенсации может быть эффективным. Также в этой публикации указывается, что если период решетки окажется очень большим, то можно использовать в решетке волнистые провода. Как будет показано ниже, незначительное искривление проводов в решетке не приводит к существенному изменению ее радиотехнических характеристик.
К сожалению, во всех патентах рассматривались варианты стенок РПУ для работы в сантиметровом и миллиметровом диапазоне длин волн. Если использовать подходы, приведенные в этих патентах для создания стенки РПУ для устройств, работающих в дециметровом диапазоне или длинноволновой части сантиметрового диапазона длин волн, то возникнут непреодолимые технологические трудности: потребуется либо неприемлемо большая толщина стенки, либо неприемлемо малая толщина провода.
В [5,6] приведен расчет радиотехнических характеристик стенки РПУ, состоящей из диэлектрических слоев и решетки из металлических проводов. Это позволяет конструировать структуры, обладающие повышенными как прочностными, так и радиотехническими характеристиками. В этих работах приводится формула для расчета коэффициента пропускания (КП) такой структуры:
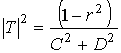 (1)
(1)
где r – коэффициент отражения (КО) диэлектрического слоя без решетки, а С и D – некоторые величины, зависящие от параметров диэлектрика и величины реактивного шунтирования решетки.
В [5] показано, что решетку из проводов, период которых меньше длины волны можно представлять в эквивалентной линии передачи в виде реактивного шунтирующего сопротивления ZЭ (рис. 2), величина которого определяется из вычисленного значения КО от диэлектрической структуры с решеткой. При этом шунтирующее сопротивление имеет индуктивный характер.
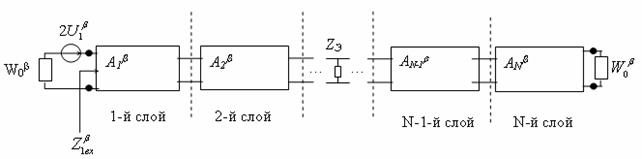
Рис. 2. Эквивалентная длинная линия для многослойного магнитодиэлектрика.
Ниже исследуются вопросы, каким должно быть это сопротивление, чтобы обеспечить наилучшие радиотехнические характеристики (РТХ) стенки РПУ. Предлагается способ увеличения величины шунтирующего сопротивления за счет использования в решетке проводов с периодическими искривлениями. Кроме этого, в отличие от [5], в работе значение ZЭ вычисляется сразу из параметров эквивалентной линии, что упростило математическую модель и облегчило численные исследования.
1. Расчет радиотехнических характеристик диэлектрических слоев, содержащих решетки с индуктивной проводимостью
В [7] представлена математическая модель, основанная на регуляризации уравнений Максвелла с помощью потенциалов Дебая, которая позволяет рассматривать плоские бесконечные магнитодиэлектрические слои в виде некоторой длинной линии. В итоге любое количество плоских магнитодиэлектрических слоев можно рассматривать как каскадное соединение четырехполюсников с матрицами передачи, элементы которых зависят от параметров слоев (рис. 2):
 (2)
(2)
где ![]() – длина участка длинной линии (толщина i-го слоя);
– длина участка длинной линии (толщина i-го слоя); 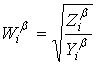 - волновое сопротивление длинной линии, описывающей i-й магнитодиэлектрический слой;
- волновое сопротивление длинной линии, описывающей i-й магнитодиэлектрический слой; ![]() - постоянная распространения волны вдоль нормали к
границе слоя;
- постоянная распространения волны вдоль нормали к
границе слоя; ![]() -постоянная распространения волны в i-м слое магнитодиэлектрика с
относительными магнитной и диэлектрической проницаемостями mi ei;
-постоянная распространения волны в i-м слое магнитодиэлектрика с
относительными магнитной и диэлектрической проницаемостями mi ei; ![]() ;
; ![]() ,
, ![]() ;
; ![]() - уголы падения волны в сферической
системе координат;
- уголы падения волны в сферической
системе координат; ![]() - индекс для обозначения электрического
(Е) или магнитного (М) типа четырехполюсника;
- индекс для обозначения электрического
(Е) или магнитного (М) типа четырехполюсника; ![]() ;
; 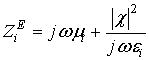 ;
;  ;
; ![]() , w - круговая частота падающее волны; k0 – постоянная распространения волны в свободном
пространстве.
, w - круговая частота падающее волны; k0 – постоянная распространения волны в свободном
пространстве.
Слоистому
магнитодиэлектрику, содержащему решетку, можно сопоставить эквивалентную схему,
представленную на рис. 3а. Для решения задачи прохождения электромагнитной
волны через слоистый магнитодиэлектрик, содержащий решетку из проводов,
необходимо найти поля, рассеянные решеткой. Сначала надо вычислить
электрические токи, наводимые падающим полем на проводах. В эквивалентной схеме
решетка представляется в виде источника тока, величина ![]() которого определяется преобразованием
Фурье по пространственным частотам тока на проводах решетки [7]. Для
определенности рассматривается случай, когда стенка РПУ имеет одну решетку,
которая обладает периодичностью только вдоль координаты Х. Так как матричный
метод позволяет найти функцию Грина и значения полей в любой точке слоистого
магнитодиэлектрика, можно составить интегральное уравнение (ИУ) для решетки из
проводов с использованием граничных условий на металле и периодических
граничных условий:
которого определяется преобразованием
Фурье по пространственным частотам тока на проводах решетки [7]. Для
определенности рассматривается случай, когда стенка РПУ имеет одну решетку,
которая обладает периодичностью только вдоль координаты Х. Так как матричный
метод позволяет найти функцию Грина и значения полей в любой точке слоистого
магнитодиэлектрика, можно составить интегральное уравнение (ИУ) для решетки из
проводов с использованием граничных условий на металле и периодических
граничных условий:
 (3)
(3)
для перпендикулярной поляризации;
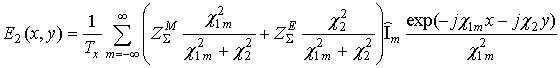 (4)
(4)
для параллельной поляризации,
где ![]() - падающее поле в области решетки, т.е.
прошедшее через верхние слои диэлектрика (точка 2 на рис. 3);
- падающее поле в области решетки, т.е.
прошедшее через верхние слои диэлектрика (точка 2 на рис. 3);
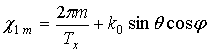 ;
;
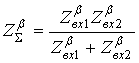 ,
,
![]() ,
, ![]() - входные сопротивления в длинной линии,
как показано на рис. 3;
- входные сопротивления в длинной линии,
как показано на рис. 3; ![]() - волновое сопротивление эквивалентной
линии передачи, описывающей свободное пространство;
- волновое сопротивление эквивалентной
линии передачи, описывающей свободное пространство; 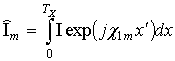 - преобразование Фурье от тока
- преобразование Фурье от тока ![]() на проводах решетки.
Все параметры линии передачи под знаком суммы вычисляются при значении
пространственной частоты
на проводах решетки.
Все параметры линии передачи под знаком суммы вычисляются при значении
пространственной частоты ![]() .
.
Из ИУ (3), (4) после
процедуры взвешивания с учетом того, что ток вдоль провода постоянный по
амплитуде, а фаза тока меняется линейно ![]() , можно найти токи на проводах решетки:
, можно найти токи на проводах решетки:
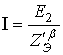 , (5)
, (5)
где  - для перпендикулярной поляризации;
- для перпендикулярной поляризации;
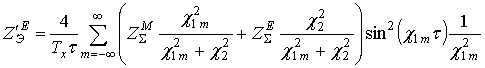 для параллельной поляризации.
для параллельной поляризации.
Так как рассматриваются только распространяющиеся гармоники, а в конструкции стенки РПУ обычно используют решетки с периодом меньшим половины длины волны, в рассеянном решеткой поле существует только нулевая гармоника. В приближении малой ширины проводов относительно длины волны можно найти величину источника тока в эквивалентной схеме:
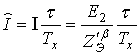 . (6)
. (6)
Можно показать, что схема на рис. 3а, где решетка проводов описывается источником тока, управляемым напряжением Е2, эквивалентна схеме на рис. 3б, где вместо источника тока стоит некоторое сопротивление ZЭ, которое можно вычислить по формуле:
 , (7)
, (7)
где b - заменяется на М для
перпендикулярной поляризации и на Е для параллельной поляризации, при этом ![]() вычисляются для 0-й
гармоники.
вычисляются для 0-й
гармоники.
Рис. 3. Эквивалентная схема для диэлектрического слоя с решеткой из проводов.
Для решеток с проводами из идеального металла с периодом меньшим длины волны [5] величина ZЭ имеет чисто реактивное значение. Для таких решеток можно ввести понятие эквивалентной индуктивности, измеряемое в Гн на квадрат поверхности:
![]() . (8)
. (8)
Таким образом, определены параметры для расчета РТХ стенки с решеткой.
2. Зависимость эквивалентной индуктивности от параметров решетки
На рис. 4 представлены расчетные частотные и угловые зависимости эквивалентной индуктивности в поверхностном сопротивлении решетки проводов с периодом Tx и шириной провода t. Эквивалентная индуктивность гораздо сильнее зависит от периода решетки, чем от ширины провода. Величина индуктивности прямо пропорциональна периоду решетки и обратно пропорциональна логарифму ширины провода. Для того чтобы две решетки с разными периодами обладали одинаковой эквивалентной индуктивностью, необходимо в решетке с меньшим периодом брать провод намного тоньше. Из рис. 4 а) б) в) следует, что решетки с равной индуктивностью и с периодом, отличающимся в два раза, должны быть сделаны из проводов с толщиной, отличающейся в 33 раза (красные и зеленые графики).

Рис. 4. Частотные и угловые зависимости эквивалентной индуктивности в поверхностном сопротивлении решетки:
а) частотная зависимость при нормальном падении волны;
б) угловая зависимость при перпендикулярной поляризации волны
в) угловая зависимость при параллельной поляризации волны
г) угловая зависимость при параллельной поляризации волны и наличии двух взаимно перпендикулярных решеток.
С увеличением периода возрастает зависимость LЭ от частоты и угла падения волны, а также от параметров диэлектрических слоев и местоположения в них решетки. Это, несомненно, приведет к сложностям при согласовании стенки в широкой полосе частот и интервале углов падения волны.
Решетки из скрещенных проводов применяются для поляризационной независимости стенки РПУ. Как следует из рис. 4 г, решетки из скрещенных проводов с контактами, имеют другую угловую зависимость при наклонном падении параллельно поляризованной волны, чем решетки из параллельных проводов. Это необходимо учитывать при расчетах. (Вычисление LЭ для решетки из скрещенных проводов осуществлялось с помощью ИУ с применением метода Галеркина). Еще можно заметить, что при наклонном падении параллельно поляризованной волны значение LЭ уменьшается. Это приведет к тому, что при различных углах падения частота согласования магнитодиэлектрика с решеткой будет разной.

Рис. 5. Частотные зависимости КО диэлектрического слоя (d=2,5мм, e=4,0) с решетками из проводов, расположенными в центре диэлектрика.
а) нормальное падение; б) перпендикулярная поляризация, q=500;
в) параллельная поляризация, q=500;
г) параллельная поляризация, q=500 (решетка из скрещенных проводов).
На рис. 5 показаны расчетные частотные зависимости КО диэлектрического слоя с параметрами d=2,5мм и e=4,0 с решетками разного периода. Решетки располагались в центре диэлектрического слоя. Хорошо видно, как зависимость LЭ от частоты и угла падения волны сказывается на качестве согласования диэлектрического слоя. Так, стенка с решеткой с периодом 30 мм при разных углах падения перпендикулярно поляризованной волны имеет разную частоту электродинамического согласования. На этих же графиках показаны частотные зависимости КО в варианте использования для согласования диэлектрического слоя некоторой поверхности с индуктивной проводимостью LЭ, не зависящей от частоты и угла падения волны. Этот вариант обеспечивает наилучшее просветление. Результаты расчетов на рис. 5 показывают, что решетки с периодами меньше чем l/3 обладают максимально близкими характеристиками с такой поверхностью. При параллельной поляризации уменьшение значения LЭ с увеличением угла падения наблюдается у решеток с любым периодом, поэтому приблизиться к идеальному случаю нельзя.
График на рис. 5г показывает проблему при использовании решеток из скрещенных проводов с контактами для согласования диэлектрических слоев. Как можно заметить, в случае падения параллельно поляризованной волны в частотной зависимости КО диэлектрической структуры с решеткой есть паразитные резонансы, из-за чего сужается полоса согласования. По-видимому, эти резонансы связаны с высшими гармониками периодической структуры, которые могут распространяться в слое диэлектрика. При отсутствии контакта между скрещенными проводами эти резонансы лежат в области более высоких частот.
Из всего выше сказанного можно сделать вывод, что для получения стенок РПУ с хорошим согласованием в широкой полосе частот необходимо использовать решетки с периодом не больше l/3, а для подбора необходимой индуктивности варьировать шириной провода. Для поляризационной независимости стенки надо использовать решетки из скрещенных проводов без контактов между ними.
3. Увеличение индуктивности решетки за счет искривления проводов в виде меандра
Хорошо известно, что при падении электромагнитной волны на тонкие диэлектрические слои часть ее отражается, причем отражение носит емкостной характер. Отражение электромагнитной волны от решетки с индуктивной проводимостью носит индуктивный характер. Отраженные поля от тонких диэлектрических слоев и от решетки частично компенсируют друг друга. Оптимальная компенсация достигается в том случае, когда амплитуда отраженного поля от тонких диэлектрических слоев равна амплитуде отраженного поля от решетки, а фазы этих полей сдвинуты на 1800. Приблизительно это условие достигается при выполнении следующего равенства:
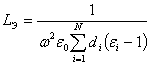 . (9)
. (9)
В (9) необходимая для согласования индуктивность решетки зависит от квадрата частоты. При уменьшении частоты индуктивность решетки надо сильно увеличивать, а значит надо увеличивать ее период. Увеличение периода возможно только до величины l/2. В дециметровом диапазоне и в нижней части сантиметрового диапазона длин волн часто необходимая индуктивность достигается только у разряженных решеток с очень тонкими проводами. Кроме этого, подбором индуктивности нельзя решить проблему согласования при наклонном падении параллельно поляризованной волны. Увеличения индуктивности в поверхностной проводимости решетки можно добиться за счет периодических искривлений проводов, входящих в ее состав. Одним из простых и максимально технологичных видов искривлений проводов является меандр – решетка изготавливается хорошо известным фотолитографическим способом на основе технологии изготовления печатных плат. На рис. 6а показан провод, изогнутый в виде меандра, а также эквивалентная длинная линия стенки РПУ, в составе которой есть решетка из проводов с дополнительной индуктивностью.
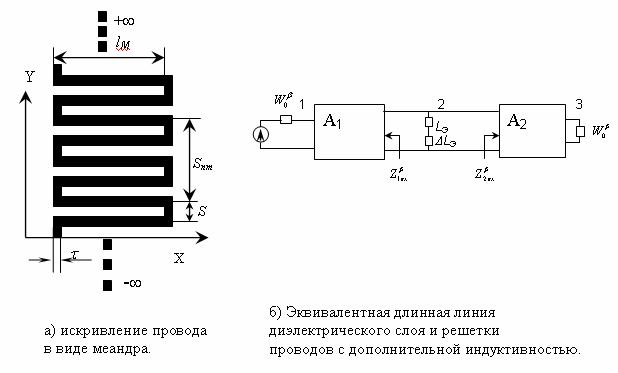
Рис. 6. Искривление проводов решетки в виде меандра для увеличения эквивалентной индуктивности.
Дополнительной
поверхностной индуктивностью в такой решетке будет индуктивность от элементов
меандра, которые помещаются на длине одного периода решетки. Это будет
эквивалентно подключению дополнительной индуктивности ![]() последовательно к LЭ (рис. 6б). Для вычисления
последовательно к LЭ (рис. 6б). Для вычисления ![]() можно воспользоваться
методом участков [8]. По методу участков общая индуктивность Lобщ конструкции равна собственной
индуктивности его участков плюс взаимная индуктивность между каждой парой участков:
можно воспользоваться
методом участков [8]. По методу участков общая индуктивность Lобщ конструкции равна собственной
индуктивности его участков плюс взаимная индуктивность между каждой парой участков:
![]() (10)
(10)
где n¹m; ![]() - собственная индуктивность участков меандра, а
- собственная индуктивность участков меандра, а ![]() - взаимная индуктивность
между участками n и m. N - количество рассматриваемых участков меандра. В общем
случае N ®¥.
- взаимная индуктивность
между участками n и m. N - количество рассматриваемых участков меандра. В общем
случае N ®¥.
По формулам [8] для высокочастотного приближения можно найти:
![]() , (11)
, (11)
где lМ – длина одного элемента меандра (рассматривается случай, когда все элементы меандра одинаковые),
 , (12)
, (12)
где ![]() - расстояние между m-м и n-м элементами меандра, S - расстояние между центрами элементов меандра.
- расстояние между m-м и n-м элементами меандра, S - расстояние между центрами элементов меандра.
Тогда ![]() в поверхностной проводимости
решетки на квадрат поверхности может быть вычислена по формуле:
в поверхностной проводимости
решетки на квадрат поверхности может быть вычислена по формуле:
![]() , (13)
, (13)
где ![]() - количество элементов меандра на расстоянии одного периода ТХ
.
- количество элементов меандра на расстоянии одного периода ТХ
.
На рис.7 показаны зависимости DLЭ от удлинения провода lпровода /l0 = lM/S + 1, вычисленные двумя способами: точным методом ИУ и методом участков. При небольшом удлинении метод участков дает большую погрешность, что связано с неравномерным распределением электрического тока на элементе меандра. При удлинении больше, чем в 10 раз, два метода дают почти одинаковые результаты. Кроме этого, искривление проводов в виде меандра дает небольшие значения DLЭ, а удлинение провода в виде меандра менее чем в два раза почти не изменяет индуктивность в поверхностной проводимости решетки.
На рис. 8 показана рассчитанная методом ИУ угловая зависимость Lобщ решетки из проводов, искривленных в виде меандра. При наклонном падении параллельно поляризованной волны Lобщ решетки из искривленных проводов меньше зависит от угла падения волны.
На рис. 9 показаны рассчитанные методом ИУ частотные зависимости КО диэлектрического слоя с решеткой из прямых проводов и с решеткой из проводов, искривленных в виде меандра с удлинением 4. Как видно, использование меандра позволяет применять более широкие провода при меньшем периоде решетки. (Для получения необходимой для согласования индуктивности в решетке с периодом Тх=10,5мм необходимо использовать провод шириной 4,2 мкм, при этом в решетке из проводов, искривленных в виде меандра, использовался провод с шириной 164 мкм). При электродинамическом согласовании тонких диэлектрических слоев с помощью решетки из изогнутых проводов можно добиться таких же частотных зависимостей КО, как при наилучшем согласовании диэлектрических слоев с помощью модельной поверхности с проводимостью, индуктивность которой не зависит от частоты и угла падения волны.
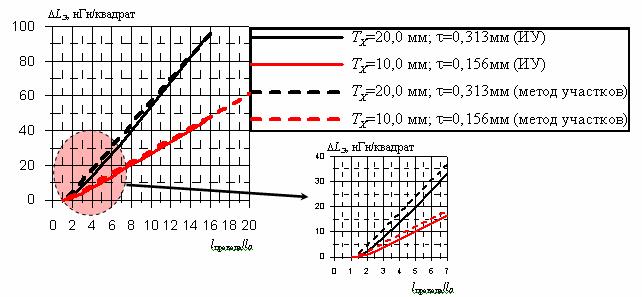
Рис. 7. Зависимость дополнительной индуктивности от относительного удлинения провода в виде меандра.
Рис. 8. Угловая зависимость эквивалентной индуктивности при разных удлинениях провода. Частота 5 ГГц. ТХ=20,0мм, t=0,625мм, S=2t. Решение методом интегральных уравнений.
В представленном на рис. 9 примере решетка из изогнутых проводов обладала DLЭ = 7,6 нГн/ квадрат. При расчете методом участков получается DLЭ = 9,2 нГн/квадрат, т. е. погрешность метода участков при таком удлинении составила 1,6нГн/квадрат.
Для получения поляризационно-независимой стенки можно использовать две взаимно перпендикулярные решетки из меандра. Наличие контакта между решетками также приводит к появлению паразитных резонансов, как и в случае с решетками из прямых проводов. Отсутствие контактов позволяет избавиться от них.
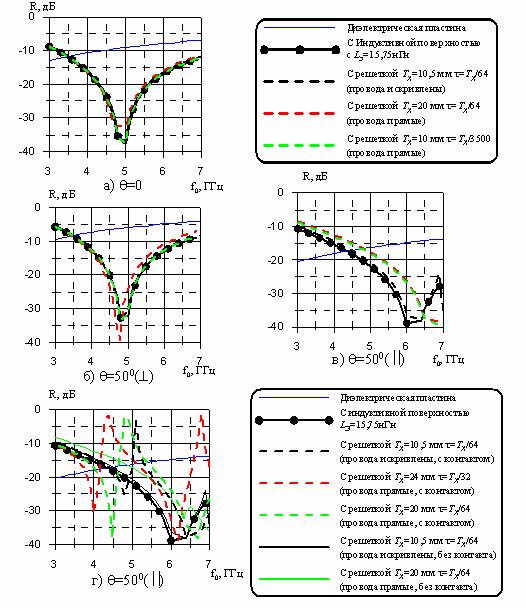
Рис. 9. Частотные зависимости КО диэлектрического слоя (d=2,5мм, e=4,0) с решетками из проводов, расположенными в центре диэлектрика.
а) нормальное падение; б) перпендикулярная поляризация, q=500; в) параллельная поляризация, q=500; г) параллельная поляризация, q=500 (решетка из скрещенных проводов).
Для примера рассмотрим случай, когда использование дополнительной индуктивности является обязательным. Необходимо спроектировать стенку РПУ с коэффициентом отражения не более -20 дБ в секторе углов от 0 до 50 градусов в диапазоне частот от 1,2 до 1,4 ГГц. Так как размеры РПУ очень большие, то для снижения веса его конструкции был выбран трехслойный вариант стенки (рис. 10). Для выполнения поставленной задачи без использования компенсационных решеток толщина сотового слоя должна быть не менее 80,0 мм. Оптимальная с точки зрения производства и эксплуатации толщина сот должна быть около 20,0 мм. Параметры диэлектрических слоев стенки показаны на рис 10. Чтобы использовать более тонкую стенку для создания РПУ с нужными электродинамическими характеристиками, надо использовать компенсационную решетку из проводов.
Из (9) можно определить, что для согласования стенки РПУ с тонкими сотами на центральной частоте рабочего диапазона индуктивность в поверхностной проводимости решетки должна быть 165,3 нГн/квадрат. Такой индуктивностью при нормальном падении волны обладает решетка с периодом TX=10 см из прямых проводов шириной 20 мкм. Однако период решетки близкий к половине длины волны в рабочем диапазоне частот приведет к сильной зависимости LЭ от угла падения волны. Кроме того, тонкие провода обладают низкой электрической прочностью и могут перегореть при мощном излучении укрываемого объекта.

Рис. 10. Трехслойная конструкция стенки радиопрозрачного укрытия с решеткой из меандра. Цифрами 1, 2, 3 обозначены места возможной установки решетки.
Использование решетки из периодически
искривленных проводов в виде меандра позволяет решить поставленную задачу. Для
определенности выберем решетку с параметрами Тx=40,0мм и t=0,625мм. Такая решетка обладает
собственной индуктивностью LЭ=30,6нГн/квадрат,
поэтому необходима ![]() нГн/квадрат. При параметре S=2t (рис. 6а) удлинение провода за счет
меандра должно быть lпровода/l0 ≈ 12, т.е. lМ=13,75мм. Более точные вычисления методом ИУ показали,
что необходимое удлинение проводов за счет их искривлений в виде меандра должно
быть равно 14, т.е. lМ=16,25мм. Рассматриваются
три случая расположения решетки в стенке РПУ: 1) в месте 1 или 3; 2) в месте 2;
3) в месте 1 и 3 (рис. 10). На рис. 11 приведены характеристики таких стенок.
Последнее расположение двухслойной решетки эквивалентно параллельному включению
в схему двух индуктивных сопротивлений, поэтому надо приблизительно в два раза
увеличить индуктивности решеток. Увеличение индуктивности было обеспечено
увеличением периода решеток до 70мм. Как можно заметить, все три варианта
обеспечивают требуемые характеристики стенки. Самый лучший – второй вариант, но
он самый сложный с точки зрения технологии производства, третий вариант
приближается по характеристикам ко второму, но является более узкополосным. В
самом технологически простом первом варианте не обеспечивается полное
согласование, но он также подходит по требуемым характеристикам. Надо заметить,
что ни одна стенка без решетки с толщиной сот 20 или 80 мм полностью не обеспечила требуемых характеристик в заданных диапазонах
частот и углов падения волны.
нГн/квадрат. При параметре S=2t (рис. 6а) удлинение провода за счет
меандра должно быть lпровода/l0 ≈ 12, т.е. lМ=13,75мм. Более точные вычисления методом ИУ показали,
что необходимое удлинение проводов за счет их искривлений в виде меандра должно
быть равно 14, т.е. lМ=16,25мм. Рассматриваются
три случая расположения решетки в стенке РПУ: 1) в месте 1 или 3; 2) в месте 2;
3) в месте 1 и 3 (рис. 10). На рис. 11 приведены характеристики таких стенок.
Последнее расположение двухслойной решетки эквивалентно параллельному включению
в схему двух индуктивных сопротивлений, поэтому надо приблизительно в два раза
увеличить индуктивности решеток. Увеличение индуктивности было обеспечено
увеличением периода решеток до 70мм. Как можно заметить, все три варианта
обеспечивают требуемые характеристики стенки. Самый лучший – второй вариант, но
он самый сложный с точки зрения технологии производства, третий вариант
приближается по характеристикам ко второму, но является более узкополосным. В
самом технологически простом первом варианте не обеспечивается полное
согласование, но он также подходит по требуемым характеристикам. Надо заметить,
что ни одна стенка без решетки с толщиной сот 20 или 80 мм полностью не обеспечила требуемых характеристик в заданных диапазонах
частот и углов падения волны.
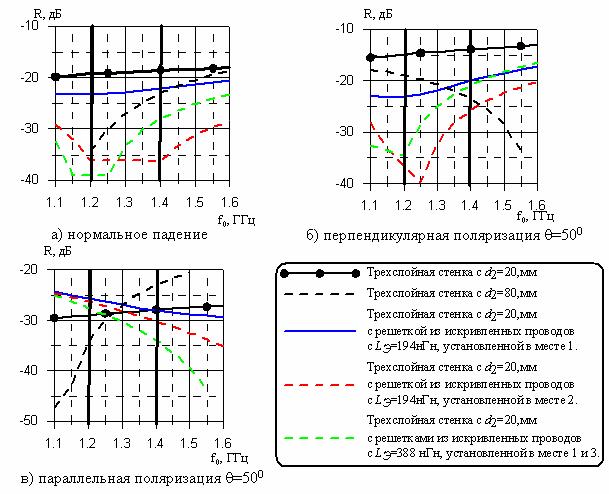
Рис. 11. Частотная зависимость КО трехслойной стенки с решеткой из проводов с периодическими искривлениями в виде меандра с удлинением lпровода /l0 =14.
4. Решетки проводов с дополнительной индуктивностью, полученной за счет искривления проводов в виде соленоида
Варианты с использованием решеток из меандра просто реализовать технологически, однако при этом возникают проблемы, связанные с получением больших значений индуктивности в поверхностной проводимости решетки. При необходимости получения большой индуктивности элементы меандра необходимо сильно удлинять, что неизбежно увеличит дополнительное отражение емкостного характера стенки РПУ в случае, когда падающее поле будет направлено вдоль элементов меандра. Это приведет в лучшем случае к сужению полосы согласования, а в худшем – к образованию паразитных резонансов, ухудшающих радиотехнические характеристики системы укрываемый объект – РПУ. В первом примере задача согласования решалась для РПУ плоской формы, использование дополнительных перпендикулярных решеток из меандра не требовалось. К тому же, в рабочем диапазоне частот элементы меандра были невелики по сравнению с длиной волны, что позволило бы использовать дополнительные перпендикулярные слои решеток, но с некоторой корректировкой на вносимую в эквивалентную линию передачи емкость. Расчет такой емкости в данной работе не рассматривается.
Обеспечить большие значения индуктивности при небольших поперечных размерах искривленных проводов позволяет трехмерное искривление проводов. Один из вариантов – это решетка из проводов, искривленных в виде соленоида (рис. 12).

Рис. 12. Искривление проводов решетки в виде соленоида для увеличения эквивалентной индуктивности.
Расчет индуктивности соленоида, состоящего из N витков, хорошо известен [8]. Дополнительная эквивалентная индуктивность в поверхностной проводимости решетки, полученная за счет искривления провода в виде соленоида, будет равна удельной индуктивности одного витка соленоида, умноженной на количество витков в одном периоде решетки:
![]() при
при ![]() , (14)
, (14)
где dс – диаметр соленоида, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - количество витков в одном периоде
решетки, S – шаг соленоида.
- количество витков в одном периоде
решетки, S – шаг соленоида.
На рис. 13 представлена структура стенки РПУ, состоящей из трех слоев диэлектрика и решетки с периодом Тх=20 мм из проводов, искривленных в виде соленоида. Параметры соленоида: t=0,5мм, dC=4,5мм, S=1,18мм. Добавочная индуктивность, полученная за счет искривления проводов в виде такого соленоида, DLЭ =289 нГн/квадрат, а общая индуктивность решетки LЭ + DLЭ =299нГн/квадрат. На рис. 14 показаны для сравнения измеренные и вычисленные частотные зависимости КО для такой структуры. Как можно заметить, решетка из искривленных проводов обеспечивает согласование трехслойной диэлектрической структуры на частоте 1,3 ГГц и существенно снижает КО в полосе от 1 до 2 ГГц. Также видно хорошее совпадение вычисленных и измеренных зависимостей, что говорит о правильности построенной модели.
В работе [2] отмечалось, что влияние проводов систем освещения или обогрева на характеристики антенны, можно компенсировать с помощью диполей. Использование искривленных проводов для этих же целей позволяет также снизить их влияние на антенну, при этом такой способ более технологичен. Из рис. 14 следует, что решетка из проводов, искривленных в виде соленоида, мало влияет на КО стенки РПУ в высокочастотной области. Это связано с низкой межвитковой емкостью и большой индуктивностью такого соленоида. Можно использовать провода, искривленные в виде соленоида с достаточно большой дополнительной индуктивностью, при этом их влияние на работу укрываемого объекта в области высоких частот будет минимальное.

Рис. 13. Структура стенки РПУ с решеткой из искривленных в виде соленоиде проводов.
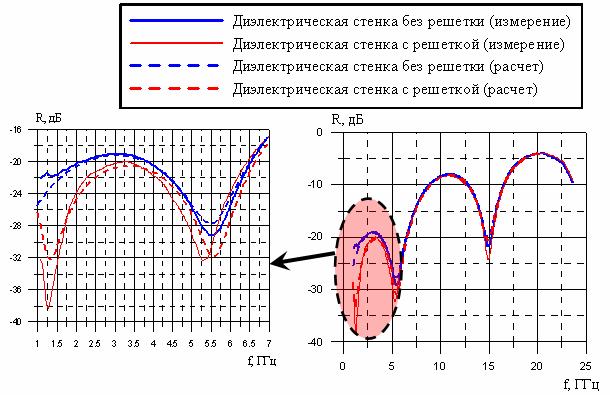
Рис. 14. Частотные зависимости КО трехслойной стенки РПУ с решеткой из изогнутых в виде соленоидов проводов.
Заключение
Из результатов проведенных исследований следует, что для наилучшего согласования диэлектрических слоев необходимо использовать решетки, эквивалентные индуктивности которых минимально зависят от частоты и угла падения волны. Такие решетки должны иметь минимальный период по отношению к длине волны. Необходимую индуктивность надо подбирать шириной провода. В дециметровом диапазоне и в длинноволновой части сантиметрового диапазона, когда нужная ширина провода становится неприемлемо узкой, LЭ нужно подбирать с помощью искривлений проводов.
Искривления проводов в виде меандра позволяют увеличивать индуктивность решетки достаточно простым и технологичным способом. При этом решетка получается планарной, что позволяет устанавливать ее между слоями диэлектрика.
Искривления проводов в виде соленоида позволяют получить очень большие величины индуктивности при малых поперечных размерах искривленных проводов. Решетки с малыми поперечными размерами проводов обладают низким уровнем отражения при поляризации волны перпендикулярно проводам. Это улучшает радиотехнические свойства стенки РПУ.
При необходимости можно получить поляризационно-независимую стенку, если использовать для согласования диэлектрических слоев две решетки с взаимно перпендикулярными проводами. Отсутствие контактов между проводами решеток позволяет избавиться от паразитных резонансов при наклонном падении на стенку параллельно поляризованной волны.
Литература
1. Кобак В.О. “Радиолокационные отражатели” М. Советское радио. 1975 г.
2. Патент US2007252775 (A1). “Radome with detuned elements and continuous wires”. Опубликован 2007-11-01. Изобретатели: MUNK BENEDIKT A [US]; DELGADO HERIBERTO J [US]; TAYLOR ROBERT [US] +. Заявитель: HARRIS CORP [US] +
3. Патент 2000114408/09, 05.06.2000. “Радиопрозрачная стенка обтекателя”. Опубликован 10.06.2001. Изобретатели: Акопян И.Г., Старков Е.А., Сухов А.М., Турко Л.С. Заявитель: Федеральное государственное унитарное предприятие – Московский научно-исследовательский институт “Агат”.
4. Патент DE102008036012(A1). “Radome for radar sensor in a motor vehicle”. Опубликован 2010-02-11. Изобретатели: PFEIFFER FLORIAN [DE], BIEBL ERWIN [DE]. Заявитель: AUDI NSU AUTO UNION AG [DE]
5. Каплун В.Л. “Обтекатели антенн СВЧ”. М.: Советское радио. 1974 г.
6. И.Г. Гуртовник и др. “Радиопрозрачные изделия из стеклопластиков”. Издательство “Мир”. Москва. 2003 год.
7. В.В. Бодров, В.И. Сурков “Математическое моделирование устройств СВЧ и антенн”. Москва, Издательство МЭИ. 1994 г.
8. П.Л. Калантаров, Л.А. Цейтлин “Расчет индуктивностей”. Издательство “Энергоатомиздат”. Ленинград. 1989 г.