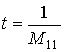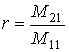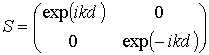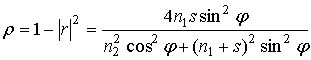РАСЧЁТ РЕЗОНАТОРА ДЛЯ СВЕРХПРОВОДНИКОВОГО ОДНОФОТОННОГО ДЕТЕКТОРА
Ю. П. Корнеева, А. В. Трифонов, Ю. Б. Вахтомин, К. В. Смирнов
Московский педагогический государственный университет
Получена 15 ноября 2011 г.
Аннотация. Произведён расчёт резонатора для сверхпроводникового однофотонного детектора. Показано, что для типичных значений сопротивления квадрата плёнки детекторов коэффициент согласования с излучением, распространяющимся со стороны диэлектрической подложки или из оптического волокна, достигает величины около 60%.
Ключевые слова: сверхпроводниковый однофотонный детектор, оптический резонатор.
Abstract. A resonator for superconducting single-photon detector is designed. Near 60% coupling with a radiation propagating from a dielectric substrate of optical fiber is demonstrated to be achieved for typical values of the detector’s film sheet resistance
Keywords: superconducting single-photon detector, optical resonator.
В связи с бурным развитием телекоммуникационных систем, появлением квантовой криптографии и созданием квантовых систем обработки информации (квантовые компьютеры), сегодня востребованы однофотонные детекторам, обладающие такими свойствами, как высокая скорость счета, низкий темновой счет, высокое временное разрешение и высокая квантовая эффективность [1]. Одним из перспективных кандидатов в ближнем инфракрасном диапазоне является сверхпроводниковый однофотонный детектор (SSPD) [2]. Квантовая эффективность данного детектора ограничена согласованием с принимаемым излучением и ограничена величиной в 30% [3]. Способом улучшить согласование и увеличить квантовую эффективность является интеграция детектора с резонатором.
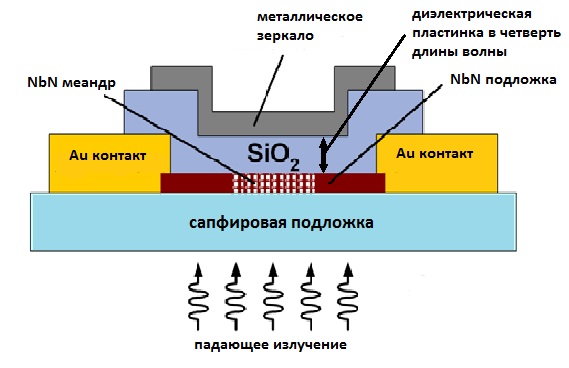
Один из вариантов геометрии резонатора для сверхпроводникового однофотонного детектора изображён на рис. 1. Электромагнитная волна падает на детектор со стороны сапфировой подложки. Чувствительный элемент детектора представляет собой сформированный электронной литографией меандр из плёнки нитрида толщиной 4 нм, занимающий площадь 7х7 или 10х10 мкм2. После прохождения чувствительного элемента электромагнитная волна распространяется в диэлектрическом подслое и отражается от металлического зеркала (плёнка золота толщиной 150-300 нм). В альтернативном варианте резонатор формируется на лицевой сторне подложки, а излучение поступает на детектор из оптического световода.
Рис. 1 Схема одного из вариантов интеграции однофотонного сверхпроводникового детектора на основе тонкой пленки нитрида ниобия с оптическим резонатором.
Принцип действия резонатора состоит в создании на чувствительном элементе детектора пучности электрического поля. В силу того, что все поперечные размеры велики по сравнению с длиной волны региcтрируемого излучения, вычисление согласования сводится к задаче о нахождении коэффициента поглощения плоской волны, падающей на слоистую структуру по нормали к плоскости слоёв. Слои отличаются от друга скоростью распространения волны в них и величиной затухания.
В силу линейности уравнений поля в рассматриваемых средах, можно ограничиться монохроматической волной. Общий вид решения волнового уравнения в этом случае известен – это две плоские волны, распространяющиеся по нормали к слоям в противоположных направлениях. Волновые числа, амплитуды и фазы волн меняются от слоя к слою, и задача отыскания решения волнового уравнения сводится к вычислению амплитуд и фаз (комплексных амплитуд).
Для решения задачи удобен подход, аналогичный описанному в [4]. Поскольку уравнения линейны, наиболее общую связь между комплексными амплитудами падающей, отражённой и прошедшей волн можно записать в виде
(1)
где M – матрица 2х2, описывающая слоистую структуру. Матрица M представляет собой произведение чередующихся в порядке следования слоёв матриц I и S, описывающих отражение и прохождение волн на границах и распространение их в слоях. Коэффициенты t и r элементарно выражаются из (1):
Вид матрицы I, соответствующей границе между средами с комплексными показателями преломления n1 и n2, устанавливается сшивкой комплексных амплитуд и первых производных от них для полей слева и справа от границы:
, (3)
Матрица S даёт связь между комплексными амплитудами волн, распространяющихся вправо и влево, на противоположных границах слоя
где k – волновое число (вообще говоря, комплексное) в веществе слоя, d – толщина слоя.
Подлежащая расчёту структура состоит из следующих слоёв: 1) сапфировая подложка; 2) тонкоплёночная NbN структура, которую ввиду малости периода структуры (200 нм) по сравнению с длиной волны можно считать однородной плёнкой с анизотропной проводимостью; 3) кварцевая четвертьволновая пластина; 4) толстая по сравнению со скин-слоем плёнка золота. В пренебрежении потерями в золоте, всё поглощение энергии поля в данной структуре происходит в плёнке NbN, поэтому коэффициент согласования равен коэффициенту поглощения структуры
. Использование формул (2) – (4) даёт
где s – отношение волнового сопротивления вакуума к сопротивлению квадрата плёнки чувствительного элемента, φ – набег фазы волны при прохождении кварцевой пластинки. Максимальное значение коэффициента согласования, соответствующее φ=π/2, оказывается равным 0.58. При расчёте были использованы следующие параметры: показатель преломления сапфировой подложки n1=1.75, показатель преломления кварцевой пластины n1=1.54 (показатели преломления соответствуют длине волны 1.55 мкм), сопротивление квадрата структурированной плёнки NbN (при поляризации падающей волны параллельной ориентации полосок меандра) R=1000 Ом. Теоретически достижимый максимум согласования (ρ=1) соответствует сопротивлению квадрата структурированной плёнки R=Z0/n1=215 Ом, что, к сожалению, достаточно далеко от типичных сопротивлений чувствительного элемента сверхпроводниковых однофотонных детекторов.
Для сравнения, посчитанный тем же методом коэффициент согласования для детектора без резонатора (NbN структура на сапфировой подложке, волна падает со стороны подложки)
(6)
оказался равен лишь 0.27. (Это число находится в очень хорошем соответствии с предельными значениям квантовой эффективности детекторов [3], что свидетельствует о справедливости приближений, использованных в расчёте).
Результаты нашего расчёта подтверждают эффективность использования резонатора описанной геометрии для согласования сверхпроводникового однофотонного детектора с излучением. Непосредственное сравнение с экспериментальными данными [6], к сожалению, затруднительно из-за отсутствия методик измерения коэффициентов отражения и пропускания для структур микронных поперечных размеров, которыми являются чувствительные элементы SSPD. Сравнение же непосредственно квантовых эффективностей детекторов, выполненных с резонатором и без такового, некорректно из-за невозможности сравнить «внутренние» квантовые эффективности детекторов (вероятности образования отклика при условии, что фотон поглотился). Однако, наличие на зависимостях квантовой эффективности интегрированного с резонатором детектора от длины волны детектируемого излучения выраженных минимумов [5] свидетельствует, в соответствии с формулой (5), об уровне согласования, близком к расчётному.
Работа выполнена при поддержке Министерства науки и образования в рамках ФЦП «Исследования и разработки по приорететным направлениям развития научно-технологического комплекса России на 2007-2012 годы».
Литература
1. R. Hughes and J. Nordholt // Science 333, 1584 (2011).
2. I. Milostnaya, A. Korneev, M. Tarkhov et al. // J. Low Temp. Phys. 151, 591 (2008).
3. Goltsman G., Minaeva O., Korneev A. et al. //IEEE Trans. Appl. Supercond. 17, 1 (2007).
4. М. Борн, Э. Вольф. Основы оптики // М., Наука, 1973.
5. A. Korneev, O. Minaeva, A. Divochiy et al. // SPIE Europe: International congress on Optics and Optoelectronics, 16-20 April 2007 Prague.
6. Манова Н.Н., Корнеева Ю.П., Корнеев А.А. и др. // Труды научной сессии МИФИ (2010) Ч.3, т. XIII, с.103