ЗАТЕНЕНИЕ ПОЛУПЛОСКОСТЬЮ С ПОЛУПРОЗРАЧНЫМ ОКОНЧАНИЕМ [1]
Д. В. Татарников, И. М. Чернецкий
Топкон Позишионинг Системс
Получена 6 декабря 2012 г.
Аннотация. Рассматриваются возможности уменьшения угловой протяженности зоны полутени при дифракции на полуплоскости, ребро которой выполнено из полупрозрачного материала. Показано, что использование материалов с реактивным импедансом слоя позволяет сократить эту зону с переходом к глубокой тени уже при малом отклонении от границы свет-тень. Результаты имеют практическое значение в вопросах электромагнитной совместимости, помехозащищенности и уменьшения ошибки многолучевости в системах локации и позиционирования.
Ключевые слова: дифракция на полуплоскости, полупрозрачный слой, зона полутени.
Abstract. Possibilities to decrease the field intensity in semi-shadow zone of the field diffracted over the edge of half-plane are dicussed. For that purpose a semi-transparent edge is treated. Both qualitative Kirchhoff analysis and strict numerical optimization are performed. It is shown that semi-transparent edge with reactive impedance allow for significant shadowing improvement versus perfect conductive one. Results are applicable to electromagnetic compatibility, jamming protection and multipath error mitigation.
Key words: Half-plane diffraction, semi-transparent sheet, semi-shadow zone.
1. Введение
Задача дифракции на идеально проводящей полуплоскости хорошо известна; полутеневая ДН описывается интегралом Френеля (см., например, [1]). Между тем, возможность получения более быстрого спадания поля при переходе через границу свет-тень представляет интерес для ряда прикладных областей. Таковы, например, задачи улучшения электромагнитной совместимости, помехозащищенности и уменьшения ошибки многолучевости в системах локации, связи и навигации. Известен подход, основанный на использовании экранов с краями в виде тонкого резистивного листа (так называемой R-карты) [2], родственные задачи рассматривались применительно к зеркальным антеннам [3]. Однако, насколько известно авторам, задача дифракции на полуплоскости, оканчивающейся полупрозрачной областью с комплексным импедансом слоя, в литературе систематически не рассматривалась. Ряд свойств экранов, выполненных из полупрозрачных материалов с комплексным импедансом слоя, изучен в [4,5]. Данная публикация является продолжением этих двух работ.
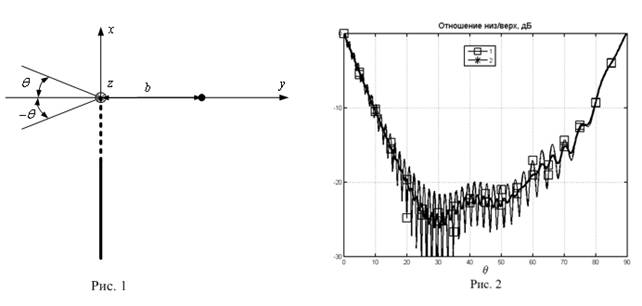
Рассматривается дифракция поля нити тока на полуплоскости. Геометрия задачи приведена на рис.1. Источник – нить тока – показан жирной точкой. Предполагается, что область вблизи окончания полуплоскости является полупрозрачной. Эта область показана жирным пунктиром. Рассматривается как Е-, так и Н- поляризация падающего поля. Раздел 2 посвящен краткому качественному рассмотрению на основе подхода Гюйгенса-Кирхгофа. Раздел 3 содержит описание численной процедуры оптимизации импеданса слоя на основе решения интегрального уравнения второго рода. В разделе 4 приводятся результаты расчета характеристик затенения для различных импедансов.
2. Апертурный анализ
Рассматривается
Н-поляризация (источник в виде синфазной нити магнитного тока). Рассмотрение
для Е-поляризации аналогично. Для случая идеально проводящей полуплоскости,
считая расстояние 
от источника до
полуплоскости (рис. 1) не слишком малым, ДН в области 
в
приближении Кирхгофа запишется в виде
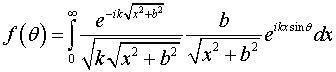(1)
Здесь
– волновое число свободного
пространства. Зависимость от времени принята в виде 
.
Главный вклад в (1) по большому параметру 
дается
[6] интегралом Френеля
(2)
Здесь
(3)
-
точка стационарной фазы. Точное решение [1] для главного вклада приводит к
такому же результату. При малых 
производная 
по абсолютной величине пропорциональна
, что и определяет ширину зоны полутени.
Напротив, для полупрозрачного окончания полуплоскости, ДН можно записать в виде
(4)
Здесь
- параметр, имеющий смысл коэффициента
прохождения. Предполагается, что 
при 
и 
при 
. В области 
главный
вклад в (4) оказывается пропорциональным [6]
(5)
что
позволяет, в принципе, более гибко управлять ДН. Более точная оценка (4)
зависит от пропорции между производными и
шириной области стационарной фазы. Не выписывая полного разложения, отметим
качественный характер данного рассмотрения, не затрагивающий возможности
практической реализации. Эти возможности обсуждаются далее на основе более
строго численного подхода.
3. Численная процедура
Предполагается, что на полуплоскости выполняются граничные условия типа тонкого слоя [7]
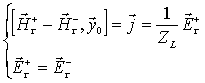(6)
Здесь
символом 
отмечены касательные к полуплоскости
компоненты, знаки +/- отмечают напряженности полей по обе стороны полуплоскости
при 
, 
- орт
оси 
, 
-
сумма токов, протекающих по двум сторонам полуплоскости, 
- импеданс слоя. Этот импеданс считается
переменным по координате х и задается в виде
(7)
Здесь
- значение импеданса слоя на краю экрана
- предполагается комплексным с неотрицательной действительной частью, 
- показатель, характеризующий скорость
убывания импеданса в области 
. В качестве
характеристики степени затенения области удобно
выбрать отношение «низ-верх»
Переход
в область тени характеризуется скоростью убывания (8) при малых . Параметры импеданса слоя , синтезировались
по критерию минимизации интеграла от отношения (8):
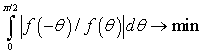(9)
На каждом шаге оптимизационной процедуры решалась граничная задача рассеяния заданного поля на полупрозрачной полуплоскости с импедансом слоя (7). Эта задача сводится к интегральному уравнению вида
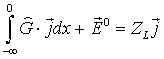(10)
Здесь
- падающее поле, 
-
тензор Грина. Уравнение (10) решалось численно методом моментов на треугольном
базисе, аналогично [4]. Для случая Е-поляризации (источник в виде нити
электрического тока) набор базисных функций разложения тока экрана дополнялся
неполным треугольником для корректного описания тока на ребре. При расчетах
полуплоскость предполагалась ограниченной с двух сторон (полоса). Протяженность
полосы по оси 
выбиралась равной 40 длин волн,
так, что вклад дифракции на нижнем относительно рис. 1 конце полосы оказывался
несущественным в интересующей области сравнительно малых .
4. Результаты расчетов
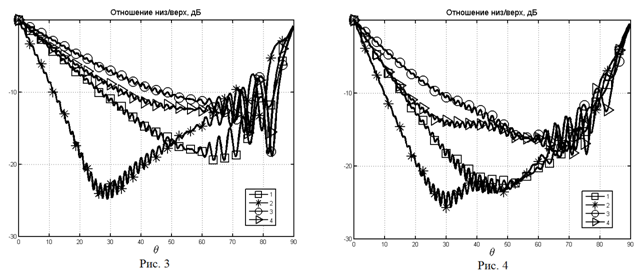
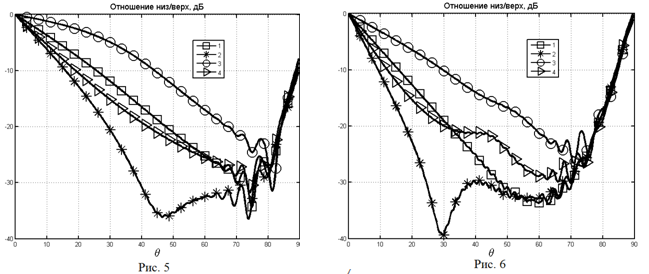
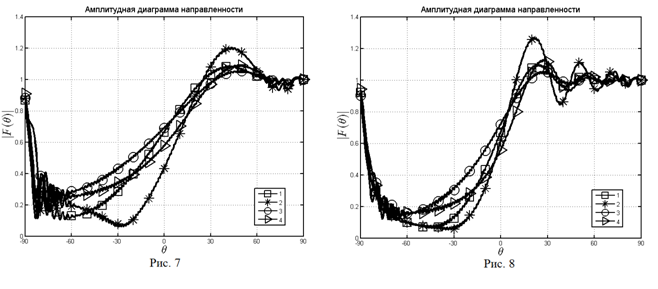
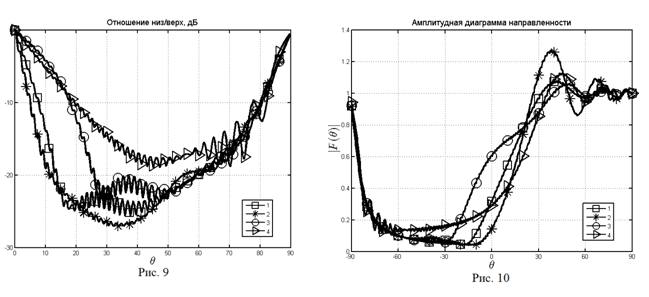
Таблица 1.
|
Рис. № |
Поляризация |
|
|
Кривая 1 |
Кривая 2 |
Кривая 3 |
Кривая 4 |
||||
|
|
|
|
|
|
|
|
|
||||
|
Рис. 2 |
|
0 |
3 |
1.2i |
4.3 |
1.2i |
4.3 |
- |
- |
- |
- |
|
Рис. 3 |
|
0 |
1 |
0.7 |
5.6 |
0.7i |
7.0 |
-0.7i |
7.0 |
0 |
0 |
|
Рис. 4 |
|
0 |
3 |
0.7 |
3.2 |
1.2i |
4.3 |
-1.2i |
4.3 |
0 |
0 |
|
Рис. 5 |
|
0 |
1 |
0.4 |
3.1 |
0.5i |
3.1 |
-0.5i |
3.1 |
0 |
0 |
|
Рис. 6 |
|
0 |
3 |
1.1 |
3 |
1.1i |
3 |
-1.1i |
3 |
0 |
0 |
|
Рис. 7 |
|
0 |
1 |
0.7 |
5.6 |
0.7i |
7.0 |
-0.7i |
7.0 |
0 |
0 |
|
Рис. 8 |
|
0 |
3 |
0.7 |
3.2 |
1.2i |
4.3 |
-1.2i |
4.3 |
0 |
0 |
|
Рис. 9 |
|
1 |
3 |
0.8 |
2 |
1.2i |
3.3 |
-0.7i |
1.5 |
0 |
0 |
|
Рис. 10 |
|
1 |
3 |
0.8 |
2 |
1.2i |
3.3 |
-0.7i |
1.5 |
0 |
0 |
Результаты
расчетов представлены на рис. 2-10. Тип поляризации и синтезированные параметры
, указаны
в Таблице 1. Дифракция на нижней, относительно рис. 1, границе полосы, приводит
к осцилляциям ДН в интересующей области сравнительно малых , а также к подъему ДН и переходу в
освещенную область при 
. Эти эффекты являются
следствием использования численной модели полуплоскости в виде полосы. Чтобы
сделать графики более удобными для обозрения, осцилляции в области сравнительно
малых сглаживались. Характер примененного
сглаживания иллюстрирует рис. 2. Здесь приведен график отношения «низ-верх»
(8), выраженного в дБ. Не сглаженной кривой соответствуют кривая 1, а
сглаженной – кривая 2. На рис. 3, 4 показано отношение «низ-верх» для случая
Н-поляризации и расстояния в 1 и 3 длины волны,
соответственно. Из графиков следует, что случай индуктивного импеданса слоя
позволяют получить заметные преимущества по сравнению с идеально проводящим
случаем. На рис. 5, 6 показаны аналогичные результаты для Е-поляризации.
Основной вывод совпадает с уже отмеченным. На рис. 7, 8 показаны амплитудные
ДН. Эти ДН рассчитаны для тех же параметров, что и рис. 3, 4. Можно отметить,
что улучшение отношения «низ-верх» за счет применения полупрозрачного окончания
одновременно приводит к некоторому росту осцилляций ДН в освещенной области 
. Однако эти осцилляции, в целом,
незначительны (на этих графиках использована шкала в относительных единицах
вместо дБ). Наконец, рис. 9, 10 иллюстрируют возможности дальнейшей оптимизации
при размещении источника на расстоянии а «ниже» границы полуплоскости. Здесь
направление 
оказывается фактически в зоне тени.
Однако, если по-прежнему определять отношение «низ-верх» согласно (8), то можно
отметить значительное улучшение по сравнению с уже рассмотренными случаями.
5. Выводы
В работе рассмотрена дифракция на полуплоскости, имеющей полупрозрачное окончание. Путем численного анализа показано, что за счет оптимизации импеданса слоя в области окончания можно получить значительное обужение зоны полутени падающего поля по сравнению с идеально проводящим случаем.
1. П. Я. Уфимцев. Теория дифракционных краевых волн в электродинамике. М.: Бином, 2007.
2. R. G. Rojas, D. Colak, M. F. Otero, W. D. Burnside. Synthesis of Tapered Resistive Ground Plane for a Microstrip Antenna, The Ohio State Univ., Columbus, Ohio, 43212-1191.
3. В. А. Боровиков, К. А. Амбарцумова. Построение параболического зеркала с краем переменной прозрачности. Радиотехника и электроника, 1990, №12.
4. D. Tatarnikov. Semi-Transparent Ground Planes Excited by Magnetic Line Current - IEEE Antennas and Propagation, v60, №6, 2012, pp. 2843-2852.
5. А. В. Вейцель, В. А. Вейцель, Д. В. Татарников. Аппаратура высокоточного позиционирования по сигналам глобальных навигационных спутниковых систем. Высокоточные антенны. Специальные методы повышения точности позиционирования / под ред. М. И. Жодзижского, М.: Изд-во МАИ-ПРИНТ, 2010 – 386с, ил.
6. М. В. Федорюк. Асимптотика. Интегралы и ряды. – М., Наука, 1987.
7. Электродинамика антенн с полупрозрачными поверхностями / под ред. Б. З. Каценеленбаума и А. Н. Сивова, Москва, Наука, 1989.