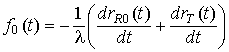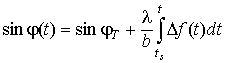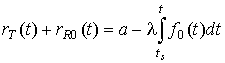УДК 621.396.96

Интегральный доплеровский метод измерения угловых координат объекта
в системах радиолокации на просвет

 

Ф. Н. Ковалев

Нижегородский государственный технический университет им. Р.Е. Алексеева

 

Статья получена 10 декабря 2013 г.

 

Аннотация. Предлагается метод определения угловых координат движущегося объекта по измерениям доплеровских частот рассеянного излучения в разнесенных приемниках просветной радиолокационной системы. Метод основан на интегрировании разности частот и оценке момента пересечения объектом направления на передатчик. Приведены результаты математического моделирования и расчет точности метода.

Ключевые слова: просветная радиолокация, многопозиционная радиолокационная система, интегральный доплеровский метод, интегрирование разности доплеровских частот, направление на объект.

Abstract. Method of estimation the direction of moving target by measuring the Doppler frequencies of the echo signal in spaced apart receivers of forward-scattering radar system is proposed. The method is based on integration the frequency differences and the estimate of moment the location of object on the transmitter direction. The results of mathematical simulation and calculation the accuracy of the method are given.

Key words: forward-scattering radar, multistatic radar system, integral Doppler method, integration the difference of Doppler frequencies, angular direction of a target.

 

Введение

Просветные радиолокационные системы (РЛС) являются наиболее простыми и вместе с этим эффективными средствами обнаружения низколетящих и Stealth объектов [1,2,3]. В основе их действия лежит эффект увеличения рассеянного излучения в направлении тени.

В последнее время интерес к просветным системам заметно возрос. В первую очередь это обусловлено их уникальными свойствами, а во вторую – быстрым развитием цифровых методов формирования и обработки сигналов и появлением компактных вычислительных устройств большой производительности.

Настоящая работа посвящена новому направлению просветной радиолокации – определению угловых координат по измерениям доплеровских частот рассеянного сигнала [4]. Рассматривается метод определения углового положения и координат объекта путем интегрирования разности доплеровских частот, измеренных в синхронизованных по времени разнесенных приемниках [5]. Для определения начальных условий интегрирования предлагается по моменту перехода через нуль доплеровской частоты рассеянного сигнала регистрировать положение объекта на направлении, в котором размещен передатчик. Метод уместно назвать интегральным доплеровским по аналогии со способом местоопределения в спутниковых радионавигационных системах [6].

Сущность метода удобно рассмотреть на просветной системе с тремя приемниками (рис. 1). Элементы системы расположены в плоскости xOy. Приемники выстроены вдоль одной прямой, совмещенной с осью Oy. Центральный приемник (Receiver)  помещен в начало системы координат – в точку O, крайние приемники  и  удалены от него на расстояние . Передатчик (Transmitter) T находится на расстоянии a от точки O на направлении  относительно оси Ox, причем . Объект движется со скоростью  в плоскости xOy, пересекая отрезок между передатчиком T и приемником  под углом  в точке S с координатами ;  – расстояние от объекта до передатчика; , ,  – расстояния от приемников , ,  до объекта. Угол  характеризует угловое положение объекта.

 

 

Рис. 1. Схема просветной РЛС

 

Разность доплеровских частот ,  рассеянного излучения, принимаемого в крайних приемниках  и ,

,

 

,    ,

 

 

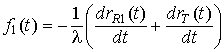определяется производной от разности расстояний  и :

,     ,

 

 – длина волны излучения передатчика, t – время. Откуда

.                                         (1)

Значение постоянной интегрирования  можно найти, используя результаты измерений зависимости доплеровской частоты рассеянного сигнала от времени в приемнике

,                                    (2)

 

и то обстоятельство, что в момент  пересечения объектом направления на передатчик T частота  принимает нулевое значение:

.                                                                   (3)

В этот же момент  величина  известна и равна , так что полагая в (1) , получим:

,

или

.                                      (4)

При выводе последних формул предполагалось, что  в несколько раз превосходит b ().

Разновидностью (4) является формула с раздельным интегрированием доплеровских частот:

.                (5)

 

Предпочтение в использовании (4) или (5) связано с особенностями технической реализации РЛС.

Точность определения угловых координат по (4) оценивалась методом математического моделирования для системы с передатчиком T расположенным на оси Ox () при следующих параметрах: , , , зона действия системы условно ограничивалась значениями ординаты . Было принято, что измерения частот в приемниках выполняются одновременно с интервалом ; ошибки измерений независимые и распределены по гауссовскому закону с нулевым математическим ожиданием и среднеквадратичным отклонением .

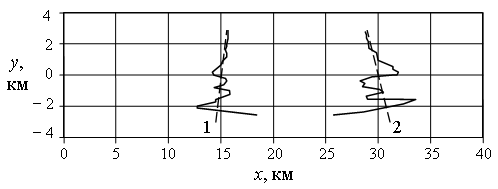
На рис. 2 показаны оценки математического ожидания  (штриховые линии) и среднеквадратичного отклонения  (сплошные линии) ошибки определения величины , вычисленные по 1000 независимым численным экспериментам. Объект двигался со скоростью  по траектории с параметрами , ,  (линии 1) и траектории с , ,  (линии 2). Траектории изображены штрихом на рис. 3. На рис. 2 время  принято равным моменту пересечения объектом оси Ox.

 

 

Рис. 2. Математическое ожидание  и среднеквадратичное

отклонение  ошибки определения величины

 

 

Рис. 3. Результаты численных экспериментов

по определению координат объекта

 

На начальных участках траекторий (до пересечения объектом прямой Ox, ) оценка угла  осуществлялась путем экстраполяции полученных к текущему моменту времени t измерений частот , ,  [7,8]. Для экстраполяции использовались полиномы первой степени, что связано с квазилинейным изменением доплеровских частот во времени при движении объекта поперек оси Ox. Коэффициенты полиномов находились методом наименьших квадратов по поступившим оценкам доплеровских частот. Начиная с десятого измерения в каждом приемнике, использовались последние десять оценок. Величину погрешности за счет экстраполяции () отражают графики  на рис. 2.

После момента  значение  оценивалось по (4) путем дискретного интегрирования оценок разности доплеровских частот. Момент  определялся по линейной аппроксимирующей зависимости, которая строилась методом наименьших квадратов по нескольким оценкам доплеровской частоты  в окрестности её нулевого значения. Полученные таким образом оценки  характеризуются графиками на рис. 2 в области t > 0. При большом числе N измерений частоты после момента  в каждом из приемников приведенная на рис. 2 зависимость  приближенно совпадала с её теоретической оценкой

 

,                                          (6)

 

получаемой из (4) для дискретной модели измерений.

Предлагаемый метод измерения направления (4) удобно использовать для определения координат объекта в просветных многопозиционных РЛС [8]. Так, в системе на рис. 1 местоположение объекта находится угломерно-дальномерным методом [9] по пересечению луча, исходящего из точки O под углом  к оси Ox, и эллипса с фокусами в пунктах размещения передатчика T и приемника . Сумма расстояний в эллипсе вычисляется интегрированием доплеровской частоты  (2) [7,8]:

 

.                                        (7)

 

На рис. 3 сплошными линиями показаны результаты двух экспериментов по оценке координат объекта с использованием (4), (7) для указанных выше траекторий и параметров системы.

Следует отметить, что для небольших  вместо  можно использовать среднее арифметическое  и :

 

.

 

Выводы

Таким образом, угловые координаты в просветных радиолокационных системах можно определить интегрированием разности доплеровских частот принимаемых сигналов в разнесенных приемниках по формуле (4). Точность получаемых оценок характеризует выражение (6). Предложенный подход удобно использовать для оценки местоположения объекта в просветных РЛС позиционными методами, например, угломерно-дальномерным – в системе с одним передатчиком и двумя либо тремя приемниками (рис. 1).

Использованный в (4) способ (3) регистрации положения объекта на направлении передатчика по измерениям доплеровской частоты (2) интересен не только для рассмотренной здесь системы. Область его применения представляется значительно шире. Например, способом (3) можно устранить неоднозначность угловых измерений в фазовых пеленгаторах интерференционного типа с большими расстояниями (базами) b между приемниками [6], . В этом случае следует производить не интегрирование разности частот, а подсчет целых циклов изменения разности фаз принимаемых сигналов.

 

Считаю своим приятным долгом поблагодарить В.В. Кондратьева за поддержку работы.

 

Результаты работы доложены на 1-й Российско-белорусской научно-технической конференции “Элементная база отечественной радиоэлектроники”, посвященной 110-летию со дня рождения О.В. Лосева, Нижний Новгород, 11-14 сентября 2013 г. [5].

 

Литература

1. Уфимцев, П.Я. Основы физической теории дифракции – М.: БИНОМ, 2011. − 351 c.

2. Чапурский, В.В. Синтезированная теневая радиоголография в бистатической радиолокации // Радиотехника. – 2009. – № 3. – С. 52 – 69.

3. Бляхман, А.Б. Бистатическая эффективная площадь рассеяния и обнаружение объектов при радиолокации "на просвет" / А.Б. Бляхман, И.А. Рунова // Радиотехника и электроника. – 2001. – Т. 46, № 4. – С. 424 – 432.

4. Ковалев, А.Н. Измерение угловых координат движущейся цели в просветных радиолокаторах с разнесенным приемом / А.Н. Ковалев, Ф.Н. Ковалев  // Труды НГТУ. – 2013. – № 4 (101). – С. 134 – 139.

5. Ковалев, Ф.Н. Интегральный допплеровский метод измерения угловых координат в просветных радиолокаторах // Труды 1-й Российско-белорусской научно-технической конференции “Элементная база отечественной радиоэлектроники”, посвящённой 110-ю со дня рождения О.В. Лосева; в 2-х т. Т.1 / Под ред. А.Э. Рассадина. – Н. Новгород: Нижегородская Радиолаборатория, 2013. –С. 244 – 247.

6. Информационные технологии в радиотехнических системах: учебное пособие для вузов / В.А. Васин, И.Б. Власов, Ю.М. Егоров [и др.]; под ред. И.Б. Федорова. – М.: МГТУ им. Баумана, 2003. – 672 с.

7. Бляхман, А.Б. Метод определения координат движущихся целей при радиолокации "на просвет" / А.Б. Бляхман, Ф.Н. Ковалев, А.Г. Рындык // Радиотехника. – 2001. – № 1. – С. 4 – 9.

8. Ковалев, Ф.Н. Определение координат движущихся целей по измерениям доплеровской частоты в радиолокационных системах с обнаружением "на просвет" // Радиотехника и электроника. – 2007. – Т. 52, № 3. – С. 331 – 339.

9. Ковалев, Ф.Н. Точность местоопределения цели в бистатической радиолокационной системе // Радиотехника. – 2013. – № 8 – С. 56 – 59.