УДК 621.396, 537.87, 535.22
ВАРИАЦИИ СКОРОСТИ СВЕТА КАК ВОЗМОЖНЫЙ ИСТОЧНИК ОШИБОК КОСМИЧЕСКОЙ НАВИГАЦИИ, РАДИОЛОКАЦИИ И ЛАЗЕРНОЙ ЛОКАЦИИ
С. А. Семиков
Нижегородский Госуниверситет им. Н.И. Лобачевского
Получена 18 декабря 2013 г.
Аннотация. Проведён анализ систематических ошибок космической навигации, радиолокации и лазерной локации космических тел и аппаратов. В частности, рассмотрены ошибки радиолокации Венеры, эффект «Пионеров», Flyby-аномалия, неравномерности вращения Луны и Земли, выявленные лазерной локацией. Рассмотрена баллистическая теория, согласно которой эти ошибки вызваны неучтённой вариацией скорости радиосигналов и света под влиянием скорости источника. Показано, что эта классическая теория во всех рассмотренных случаях верно предсказывает порядок величины и знак ошибок, а учёт вариаций скорости света и учёт переизлучения средой позволяет существенно снизить величину систематических ошибок.
Ключевые слова: радиолокация планет, космическая навигация, скорость света, баллистическая теория, лазерная локация Луны, GPS, ГЛОНАСС.
Abstract: Analysis of systematic errors in astronavigation, radiolocation and laser ranging of astronomical objects and spacecraft is carried out. In particular, errors of radiodetermination of Venus, Pioneer effect, Flyby anomaly and irregularities of the Moon and Earth rotation detected by laser ranging are studied. The ballistic theory is analyzed according to which these errors are caused by unaccounted variations of radio signal and light velocities which, in their turn, are caused by influence of source velocity. It is shown that this classical theory predicts the correct value and sign of the error in all the studied cases and consideration of variability of light velocity as well as consideration of reemission of the light by the medium allows to relevantly decrease the value of systematical errors.
Key words: planetary radar, astronavigation, speed of light, ballistic theory, Lunar laser ranging, GPS, GLONASS.
Посвящается памяти В.П. Селезнёва – первого космонавигатора
Введение
Астрономические измерения положений планет и космических аппаратов сводятся к двум основным методам – к измерению их геоцентрических углов φ и θ (азимута и высоты, или прямого восхождения и склонения) и дистанций r, то есть, по сути,– к измерению их положений в сферической (r, θ, φ) системе координат. Если классические астрономические измерения на базе телескопов и радиотелескопов основаны на измерении угловых координат, то измерения на основе лазерной локации и радиолокации позволяют определять расстояния, а также лучевые скорости движения – по доплеровскому сдвигу частоты отражённого сигнала. Как показала история астрономии и радиоастрономии, эти методы измерения координат, с одной стороны, дополняют друг друга [1], а с другой,– зачастую противоречат друг другу и дают не согласующиеся между собой результаты, особенно если измерения ведутся вдоль протяжённых участков орбит, и дополнительно учитываются законы небесной механики.
Как правило, в случае таких противоречий предпочтение отдают дальномерным измерениям, ввиду их огромной точности, достигающей при локации Луны нескольких сантиметров [2], а при радиолокации внутренних планет – нескольких километров [3]. Это на порядки превышало точность угловых оптических измерений и соответствующих им линейных погрешностей. Высокая точность измерения расстояний r = cτ/2 обусловлена огромной точностью измерения времени задержки τ отражённого сигнала (летящего со скоростью c), доходящей до 10–14 с при зондировании фемтосекундными лазерными импульсами [4]. Для данных лазерной и радиолокации высокую точность подтверждают и малым разбросом значений дистанций, измеренных в течение одного сеанса локации или в разных сеансах на одних и тех же участках орбиты. Однако столь высокая точность свидетельствует лишь о малости случайных погрешностей, но не исключает существования больших постоянных систематических ошибок лазерной и радиолокации, выявить которые можно лишь при сравнении их данных с данными других методов.
Действительно, как покажем далее, результаты дальномерных измерений в ряде случаев расходятся с теоретическими значениями расстояний и с данными визуальных угломерных измерений, причём на величину, превышающую погрешность последних. Это позволяет предположить наличие систематических ошибок радио- и лазерной локации. Поскольку точность измерения времени задержки сигнала τ надёжно контролируется, то ошибки могут быть связаны лишь с неточностью принятого значения скорости света c [5], причины чего рассмотрим далее.
2. Ошибки и аномалии радиолокации планет
За прошедшие полвека сеансы космической радиолокации и лазерной локации, проведённые в СССР, России и США, выявили ряд аномалий в виде превысивших возможные ошибки систематических отклонений измеренных скоростей и расстояний космических тел и аппаратов от расчётных [6]. Ввиду растущей точности методов и процедур расчёта на ЭВМ, в последние годы выявляют всё больше подобных аномалий [7].
Пионер космической навигации В.П. Селезнёв [8–10], американский физик Б. Уоллес [11–13] и ряд астрономов [5] назвали в качестве возможного источника таких ошибок – отклонения скорости сигналов от применяемого в расчётах номинального значения скорости света c, предписанного специальной теорией относительности (СТО). Тогда как по баллистической теории Ритца (БТР) в космическом вакууме скорость света c' = c + v зависит от скорости источника v, которая векторно, механически добавляется к номинальной скорости c сигнала, подобно тому, как скорость движущегося орудия добавляется к скорости выпущенного им снаряда (отсюда название теории). Само по себе непостоянство скорости света в космическом вакууме не подвергают сомнению и даже подтверждают прямыми экспериментами [14]. А эффект звёздной аберрации и другие случаи относительного движения источника и приёмника подтверждают, что скорость источника влияет на скорость испущенного им света. Однако в рамках СТО считалось, что скорость источника влияет лишь на направление скорости испущенного им света, но не влияет на её величину. То есть в СТО имеет место парадоксальная ситуация, когда к скорости света добавляется поперечная составляющая скорости источника (меняющая направление света), но не добавляется продольная, которая заметно меняла бы скорость света по величине.
Тем не менее, зависимость величины скорости света от скорости источника не противоречит данным экспериментов [15–17] и косвенно подтверждается данными лабораторных опытов [18, 19] и астрономических наблюдений, объясняя ряд космических аномалий [15, 20–23]. Проведённый Де Ситтером анализ наблюдений двойных звёзд, в течение целого века приводившийся в качестве противоречия баллистической теории [24], как выяснилось, не имеет доказательной силы. Астрономы П. Гутник [25] и Э. Фрейндлих [26] показали ровно век назад, в 1913 г., в ответ на критику Де Ситтера, что искажения видимых звёздных движений под влиянием скорости звёзд на скорость испущенного ими света реально наблюдаются в виде эффекта Барра [15, 27, 28]. Кроме того, как показал американский физик Дж. Фокс, на пути света к Земле по теореме погашения (экстинкции) Эвальда-Озеена исходный свет звезды постепенно гасится облаками межзвёздного газа и переизлучается ими со скоростью c относительно облаков. Для света с длиной волны λ, при концентрации атомов N ~ 1 см–3 и показателе преломления n межзвёздного газа, Фокс оценил характерную длину переизлучения
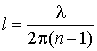 (1)
(1)
в один световой год [28]. Соответственно, искажения видимого движения звёзд, вызванные влиянием скорости источника на скорость света и пропорциональные пути l, на котором скорость света отличается от c, окажутся много меньше ожидаемых Де Ситтером. Переизлучение, как показал Фокс, следует учесть и в ряде других земных и космических экспериментов, где существенно переизлучение света средой. Таким образом, даже незначительные искажения и аномалии, выявленные за целый век в астрономических наблюдения и опытах по проверке баллистической теории [27, 29–31], могут косвенно свидетельствовать о влиянии скорости источника на скорость света, если учесть эффект переизлучения.
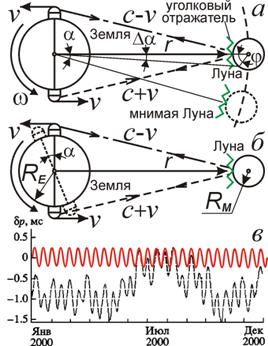
Уже в 1960-х гг. в первых успешных сеансах радиолокации Венеры, осуществлённых группой В.А. Котельникова в СССР и группой И. Шапиро в США, выявили систематические расхождения (на сотни километров превысившие возможные ошибки) между измеренными радарами положениями планеты и её предвычисленными положениями – эфемеридами, рассчитанными из данных астрономии [32–34]. Как показал Б. Уоллес [11, 12], расхождения снизятся в разы, если учесть баллистическую зависимость скорости света от скорости источника – радара на Земле, движущегося со скоростью v ввиду осевого вращения Земли, вращения системы Земля-Луна и обращения вокруг Солнца. От сообщения радиолучу скорости v меняется его скорость c + v и время τ движения сигнала, по которому ищут расстояние r Земля-Венера (рис. 1). В итоге, расчётное расстояние cτ (или cτ/2, с учётом времени движения отражённого луча), найденное из постоянной скорости света c, отличается от истинного расстояния (c + v)τ.
Рис. 1. Схема движения Земли и Венеры возле нижнего соединения, в приближении круговых орбит.
Влияние осевого вращения Земли, сообщающей свою окружную скорость (~ 500 м/с) радиолучам, проявилось, например, в том, что радиолокационные станции СССР и США, расположенные в противоположных точках Земли и синхронно измерявшие расстояния до Венеры, получали разные значения. Причём, как отмечено Б. Уоллесом [11, 12], А.К. Шуруповым [35], С.А. Базилевским и В.И. Секериным [36], систематически больше получалось значение расстояний у станций, которые в ходе суточного вращения в момент измерения отдалялись от Венеры и по баллистической теории снижали скорость радиосигнала, ведя к избытку времени запаздывания и расчётной дистанции. А у станций, приближавшихся к Венере, расстояния получались систематически меньше, что можно было связать с увеличением скорости радиосигнала и уменьшением времени запаздывания τ.
Одной из целей радиолокации Венеры было уточнение астрономической единицы (а.е.) – радиуса земной орбиты R2 (среднего расстояния Земли от Солнца). Измерив радаром расстояние r Земля-Венера, из углов в треугольнике SVE (Солнце-Венера-Земля) вычисляли расстояние R2 Земля-Солнце, пропорциональное r. Но, вопреки названию, расчётная а.е. регулярно менялась [5] с периодами, равными суткам, месяцу и синодическому году Венеры, с которыми меняется относительная скорость Земли, вносящая отклонения в расчётные дистанции Венеры и в R2 [11, 12]. Измеренное радаром значение а.е. отличалось и от значения, измеренного визуальными методами астрометрии. Причём разница превышала погрешность этих методов, что не нашло объяснений [5, 32], хотя ожидалось по баллистической теории.
Венера тоже сообщает при сближении свою скорость vr отражённому сигналу, и он достигает Земли за меньшее время τ, занижая расчётное r. После предельного сближения с Землёй в нижнем соединении, Венера удаляется, скорость сигнала становится ниже c, и он тратит большее время τ, завышая r. Оттого до соединения расчётные значения дистанции Земля-Венера r' = cτ/2 и астрономической единицы получались ниже реальных, а после соединения – выше (рис. 2) [5].

Рис. 2. Значения астрономической единицы в зависимости от даты сеанса радиолокации [5, с. 190] (нижнее соединение – 11 апреля 1961 г.).
Если учесть, что сигнал лишь к Венере идёт со скоростью с относительно Земли, пролетая путь r за время τ1 = r/c, а отражённый сигнал при лучевой (радиальной) скорости Венеры vr вернётся со скоростью c' = c – vr за время τ2 = r/c', то общая задержка τ = τ1 + τ2 = r/c + r/c'. Найденное из номинальной скорости с расстояние r' = сτ/2 ≈ r + rvr/2c превысит реальное r на Δr = rvr/2c. Из треугольника SVE в приближении круговых орбит планет (рис. 1) лучевая скорость Венеры vr = (ω1 – ω2)R1R2·sin(α)/r, где ω1 = 3,2·10–7 рад/с, ω2 = 2·10–7 рад/с – угловые гелиоцентрические скорости, соответственно, Венеры и Земли, R1 = 108·109 м, R2 = 150·109 м – радиусы их орбит, α = (ω1 – ω2)t – гелиоцентрический угол VSE между ними, а t выражено в сутках, истёкших с момента нижнего соединения. Тогда систематическое отклонение расстояния, выраженное в километрах, найдётся как
Δr = r' – r = (ω1 – ω2)R1R2·sin[(ω1 – ω2)t]/2c ≈ 3350·sin(0,011t) км. (2)
То же отклонение, выраженное в световых секундах (по времени задержки), есть
Δτ = Δr/c ≈ 0,011·sin(0,011t) с. (3)
Фактически наблюдаются именно такие вариации систематических ошибок-невязок расстояний Δr (рис. 3.а) или времён Δτ (рис. 3.б), т.е. разностей измеренных τo и вычисленных τc по таблицам Ньюкома. Внесение этих поправок (2) и (3), учитывающих баллистический принцип, снижает систематические отклонения: остаются лишь случайные ошибки, которые ещё снизятся, если учесть влияние вращения Земли на скорость сигналов [11, 12], а также переизлучение межпланетной средой. По мере роста дистанции r и слоя пройденной межпланетной плазмы переизлучённый ею сигнал восстанавливает скорость c, отчего отклонения перестают расти с отходом от нижнего соединения (рис. 3). Эффективность этого переизлучения можно оценить, сопоставляя r с толщиной переизлучающего слоя плазмы l = λ/2π(n – 1), согласно формуле (1), на основе рассчитанного для данной длины волны λ показателя преломления n, оцениваемого по измеренной концентрации межпланетной плазмы, газов и пыли.
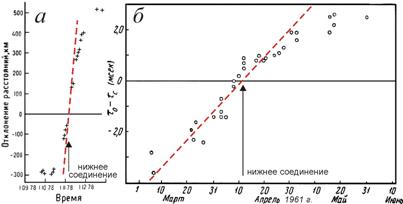
Рис. 3. Отклонения радарных расстояний Венеры от эфемеридных (по таблицам Ньюкома), измеренные в километрах (а, кресты) [1] и световых миллисекундах (б, кружки) [5, с. 242], в сравнении с предсказанными зависимостями (2) и (3) по теории Ритца (пунктир).
Влиянием переизлучения плазмы можно, в частности, объяснить несовпадение ~ 1000 км (выходящее за пределы ошибок радарных методов) значений астрономической единицы, измеренных разными радарными станциями на разных частотах 408 – 2388 МГц [37]. Действительно, на разных частотах различаются показатели преломления n и длины переизлучения l, а значит и дистанции, в пределах которых скорость радиосигнала, отражённого движущейся Венерой, отличается от c. Причём, как отмечено [37], эти различия нельзя списать на дисперсию межзвёздной среды, которая всегда приводила бы к получению меньшего расстояния, измеренного на коротких волнах, чем на длинных. А фактически наблюдалось «отсутствие видимой связи между полученными значениями астрономической единицы и частотой» [37]. Согласно баллистической теории, такой чёткой связи и не должно быть, раз на измеренную величину астрономической единицы влияет не только частота зондирующего сигнала (и длина переизлучения l), но и знак, и величина лучевой скорости Венеры, а значит,– и даты сеансов радиолокации, которые, так же как частоты, различались у разных обсерваторий.
Поскольку систематические расхождения данных радиолокации с эфемеридами не удавалось объяснить, расхождения формально устраняли коррекцией эфемерид, например, внося поправки Данкомба, «сместившего» Венеру вперёд по орбите на 290 км, то есть увеличившего гелиоцентрическую долготу Венеры на 0'',55 [5]. Поскольку даже при этом остались расхождения, Венеру сместили ещё на 270 км, увеличив её гелиоцентрическую долготу ещё на 0'',52 [38] и построив численную теорию движения планеты, соответствующую данным радаров [1]. Тем не менее, систематические расхождения в сотни км (соответствующие ошибке небесных координат Венеры ~ 1'') радарных данных с таблицами Ньюкома-Данкомба и с визуальными данными всё время сохранялись [1, 3, 39] и до сих пор не объяснены. Согласие этих двух типов данных, как отмечено,– всего лишь удовлетворительное [3].
Хотя принято считать, что значительные отклонения (~ 1000 км) имели место только в первых сеансах радиолокации, а в ходе уточнения её методов ошибки снизились на порядки, фактически эфемериды постепенно корректировали по данным радаров. В ходе таких итераций результаты каждых последующих радарных замеров всё меньше расходились с эфемеридами [33, 40], претерпевавшими одну редукцию за другой. Однако систематическая ошибка измеренных положений Венеры,– в виде расхождения радарных измерений с визуальными угломерными измерениями,– сохранялась на протяжении десятков лет на уровне Δ ~ 1'' ~ 5·10–6 рад [3, 40], хотя астрономические приборы (особенно основанные на методах интерферометрии), тоже совершенствовались. К настоящему времени их точность существенно выросла, достигая сотых и тысячных долей угловой секунды. Таким образом, систематическая ошибка Δ ~ 1'' в длительных рядах наблюдений на порядок превышает точность прежних астрометрических методов (и на порядки превышает современную точность астроинтерферометров и радиотелескопов), соответствуя на дистанции Венеры систематическому смещению порядка R2Δ ~ 750 км вперёд по орбите.
Эти ошибки ярко проявились и в 2004, 2012 гг. при наблюдении астрономами прохождения Венеры по диску Солнца: моменты контакта планеты с диском Солнца отставали на время t порядка минуты [41, 42] от эфемеридных, содержащих радарные «поправки» [1], сместившие Венеру вперёд по орбите на сотни километров. Поскольку за это время t ~ 1 мин угловое смещение Венеры относительно Земли α = (ω1 – ω2)t, а линейное – αR1 = (ω1 – ω2)tR1 ≈ 500 км, то можно предположить, что задержка вызвана именно ошибочным «смещением» планеты вперёд по орбите на основе радарных данных. Это можно проверить более точными замерами положений Венеры с использованием современных телескопов и радиотелескопов со сверхдлинной базой (РСДБ), поскольку радиоизлучение горячей поверхности Венеры отчётливо регистрируется [43]. Измерение положений Венеры при этом можно производить либо по измерению моментов покрытия Венерой точечных радиоизлучающих объектов с точно измеренными небесными координатами, либо непосредственно – по данным радиоинтерферометров со сверхдлинной базой, либо – по триангуляционным измерениям на базе порядка диаметра Земли, с разнесённых сетей радиоинтерферометров.
Подобные сравнительные измерения положений и орбитальных элементов по данным дальномерных, доплеровских и угломерных измерений интересно произвести и для других планет, особенно для Меркурия и Марса. Для них рассчитанные по данным радаров орбиты и положения тоже содержат заметные систематические расхождения (достигающие 400 км) с аналитической теорией Ньюкома и эфемеридами, рассчитанными по визуальным астрономическим наблюдениям [3, 44]. Для этих планет, ввиду их высоких орбитальных эксцентриситетов, можно ожидать ещё больших расхождений и невязок, чем у Венеры. Из-за переменной скорости движения по орбите радарные ошибки нельзя полностью скорректировать добавлением постоянного смещения по орбите. Но, разумеется, численная теория движения планет, построенная по данным радиолокации, всё же лучше согласуется с последующими радарными измерениями (содержащими те же систематические ошибки), чем с данными аналитической теории Ньюкома, построенной по визуальным наблюдениям планет [45].
Ошибки радиолокации могут сыграть роковую роль и при расчёте орбит астероидов, пересекающих орбиту Земли и близко подходящих к планете, особенно в свете не спрогнозированного падения Челябинского (Чебаркульского) метеорита. Поэтому, для своевременного предотвращения астероидной опасности, точность радиолокации следует всесторонне проверять, совершенствовать её методы, повышать дальность и чувствительность космических радаров.
3. Ошибки радиолокации космических аппаратов
На ложный «сдвиг» Венеры по орбите впервые обратил внимание космический навигатор, обучавший первые отряды космонавтов,– проф. В.П. Селезнёв [8], сотрудник С.П. Королёва и автор монографии «Навигационные устройства» (М.: Оборонгиз, 1961), создавший навигационные системы первых космических кораблей. Селезнёв показал, что без учёта баллистической теории «на основе научных сведений о свете астронавигация в принципе невозможна» [46, с. 308]. Он же отметил значение баллистической теории в навигации АМС и космических зондов, ряд аварий которых, скажем у аппаратов «Фобос-I» и «Фобос-II», вызван радарными ошибками [8–10, 46].
Не исключено, что и аварии ряда других аппаратов, посланных в разные годы к Венере и Марсу, вызваны систематическими ошибками измерения положений аппаратов и планет на основе данных радиолокации. Очевидно, радарные измерения элементов орбит оказываются более точными, если речь идёт об измерении радиусов орбит планет (их больших полуосей). Именно эти характеристики играют основную роль в расчётах траекторий аппаратов. Поэтому без радарных замеров неточности в значении астрономической единицы и радиусов орбит других планет вели бы к значительным промахам аппаратов мимо планет, достигающим нескольких диаметров планеты типа Венеры или Марса [1, 37]. Менее критичным параметром является положение планет на орбите, для определения которого больше подходят астрономические угловые измерения. Поскольку траектория движения АМС по переходной орбите (например, по орбите Гомана) проходит практически по касательной к орбите планеты, то неточности в определении положения на орбите скажутся лишь на моменте, когда аппарат пройдёт возле планеты, а дистанция предельного сближения практически не изменится. Тем не менее, и в этом случае ошибки в измерении положения аппарата и планеты могут приводить к авариям и промахам, с чем В.П. Селезнёв и связывал ряд аварий АМС, посланных к Венере и Марсу.
Рассмотрим в этом ключе эффект «Пионеров» [47, 48] – аномалию, выявленную в числе прочих Лабораторией Реактивного Движения (JPL NASA). Скорости АМС «Пионер-10» и «Пионер-11», измеренные радарами (по доплеровскому сдвигу частоты сигнала от АМС), отличались от расчётных [7]. Измеренное ускорение «Пионеров» в поле тяготения солнечной массы M превысило расчётное ускорение a' = GM/r2 на величину Δao = (8,74 ± 1,33)·10−10 м/с2 (на расстоянии r Урана [48]). Если «Пионеры», улетая от Солнца и Земли со скоростью v ≈ 10 км/с, излучали сигнал со скоростью c – v, наращивая его запаздывание τ, то по номинальной скорости сигнала c решали, что скорости и ускорения АМС измерены на расстоянии r' = сτ ≈ r + rv/c, а не на истинном r = (c – v)τ, где тяготение Солнца и ускорение a = GM/r2 выше расчётного a' = GM/r'2 на
Δac = a – a' ≈ 2av/c = 2vGM/cr2. (4)
На дистанции Урана r ≈ 3·1012 м при v ≈ 10 км/с это составит расчётную величину Δac ≈ 9,9·10–10 м/с2, близкую к измеренной Δao ≈ 9·10–10 м/с2 [48]. Сходные аномалии выявлены у АМС «Улисс» [49] и «Кассини», у которого на расстоянии Сатурна (r ≈ 1,5·1012 м) измеренный избыток ускорения Δao ≈ 3·10−9 м/с2 [50] близок к расчётному Δac = 2vGM/cr2 ≈ 4·10–9 м/с2.

Рис. 4. Схема радиолокации АМС «Пионер» (вверху)
Отметим, что основная гипотеза, объясняющая аномальное ускорение «Пионеров» радиационными силами от неравномерного нагрева корпуса изотопным источником [51], вызывает сомнения, поскольку аномальное ускорение характерной величины и направления обнаружено у ряда других АМС, имеющих принципиально разные конструкции и источники питания. Поэтому маловероятно, чтобы во всех случаях возникала одна и та же сила, направленная к Солнцу. Кроме того, корпус «Пионеров» в целях термоизоляции покрыт отражающей плёнкой с золотым покрытием, плохо излучающим тепло. Отражение и переизлучение плёнкой, поверхность которой имеет неопределённую сложную форму,– это задача, неподвластная даже численному моделированию. От размещения плёнки на стороне аппарата, обращённой от Солнца, излучение тепла там может быть не выше, а ниже, чем со стороны антенны (обращённой к Солнцу и Земле), где радиационная сила обратная. То есть, радиационные силы не только ниже расчётных в [51], но и могут даже иметь обратное направление. Согласие величины радиационного ускорения с измеренным обусловлено выбором коэффициентов, характеризующих связь нагрева и радиационных сил [51].
Малость радиационных сил следует также из того, что неравномерный нагрев корпуса «Пионеров» (демонстрирующий смещение области максимального нагрева на h ~ 1 м от оси аппарата [51]), создав радиационную силу F и ускорение Δao =F/m ~ 10−9 м/с2, создал бы также и момент силы M = Fh (рис. 5), который за двадцатилетний срок t неуправляемого полёта отклонил бы оси «Пионеров» и жёстко с ними связанных параболических антенн на угол α, исключающий обмен сигналами с Землёй. У «Пионеров» не действуют реактивные системы стабилизации направления. Направление оси аппарата стабилизируется исключительно вращением с угловой скоростью ω = 4,8 об/мин ≈ 0,5 рад/с и моментом импульса Iω ~ md2ω/8 ~ mh2ω вдоль оси аппарата, у которого момент инерции I можно оценить как момент инерции диска диаметром d = 2,7 м. Поэтому постоянно действующий момент M, поперечный к этой оси, за время t сообщил бы аппарату поперечный момент импульса Mt и развернул бы ось аппарата на угол α = arctg(Mt/Iω) ~ arctg(Δaot/ωh) ~ 50°, полностью лишив связи. При рабочей частоте 2292 МГц (λ = 0,13 м) и диаметре антенны d = 2,7 м главный лепесток её диаграммы направленности намного более узок: φa ≈ λ/d = 0,048 рад ≈ 3°. Если исходно антенна была направлена к Земле, то при развороте аппаратов на угол arctg(Δaot0/ωh) ~ φa/2 связь пропала бы уже спустя время t0 ~ ωh·tg(φa/2)/Δao ≈ 0,4 года их свободного полёта,– задолго до пересечения орбиты Урана. Тот факт, что связь сохранялась десятилетиями, вплоть до пересечения орбиты Плутона и далее, свидетельствует о сохранении направления осей «Пионеров» в пространстве и отсутствии заметных радиационных или иных неучтённых сил.

Рис. 5. Асимметричное распределение температуры по корпусу «Пионеров» [51], создавая радиационную силу F и аномальное ускорение Δao, вело бы к появлению момента M, отклоняющего антенну АМС в сторону от Земли.
Открыта и Flyby-аномалия [48, 49], т.е. невязки ожидаемых скоростей и измеренных радаром у АМС, пролетающих мимо планет по гиперболической траектории. Так, у АМС «Галилео», «NEAR», «Розетта» после пролёта мимо Земли выявлен прирост скорости на величину порядка нескольких мм/с, вопреки закону сохранения энергии. Вероятная причина ошибок – применение в измерениях скорости аппаратов релятивистской формулы доплер-эффекта
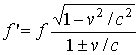 , (5)
, (5)
согласно которой при сближении частота f повышена до f1 ≈ f(1 + v/c + v2/2c2), а при удалении – снижена до f2 ≈ f(1 – v/c + v2/2c2). В классической физике
f1 = f(1 + V/c) и f2 = f(1 – V/c), (6)
причём в космосе измерены именно такие симметричные смещения частоты: f1 – f = f – f2. То есть, если исходить из классических формул, скорость V аппаратов сохраняется. Однако, рассчитывая скорость по СТО, получают, приравнивая измеренные частоты (6) к релятивистской частоте (5), что при сближении v ≈ V – V2/2c, а при отдалении v ≈ V + V2/2c, отсюда – ложный вывод о приросте скорости на величину ∆v ≈ V2/c. При скорости АМС V ~ 103 м/с это как раз создаст иллюзию прироста скорости ∆v ~ 1–10 мм/с.
Также и у спутников Луны, Земли и других планет аномалии движения могут быть связаны не только с аномалиями гравитационного поля (масконами), но и с систематическими ошибками радиолокации от неучёта вариаций скорости света и применения формул СТО. Возможно, из-за этого более высокую точность дают измерения гравитационных аномалий с применением двух спутников (например, «Эбб» и «Флоу» в миссии «Grail» NASA), летящих по орбите один за другим и посредством радиолокации и замера доплеровских сдвигов выявляющих вариации относительной скорости и дистанции между спутниками, при входе в зоны аномалий. Так же и японский зонд «Кагуя», летящий по низкой орбите вокруг Луны, выявляет гравитационные аномалии путём радиолокации со спутника-ретранслятора «Окина», летящего по более высокой орбите. С одной стороны, это позволяет поддерживать связь с Землёй и проводить измерения, когда один из спутников входит в область радиотени Луны, а с другой,– позволяет проводить относительные измерения с более высокой точностью, чем при измерении абсолютных расстояний спутников до Земли. Это связано не только с увеличением ошибок по мере роста расстояния и переменной задержкой радиосигнала в ионосфере Земли, но и с тем, что относительная скорость спутников, особенно движущихся друг за другом по одной орбите, мала (по сравнению со скоростью относительно Земли). Поэтому её влияние на скорость сигнала и погрешности в измерении расстояния – пренебрежимо малы.
Ошибки выявляют и сети спутников GPS и ГЛОНАСС [52], использующие метод радиолокации с наземных станций слежения и группы искусственных спутников. Навигационный модуль в мобильном устройстве «ловит» радиосигналы, посланные спутниками и содержащие информацию о положении каждого спутника (отслеживаемом станциями) и времени излучения сигнала (по атомными часам на спутнике). Вычитая это время из времени приёма сигнала, мобильный приёмник по времени τ движения радиоимпульса рассчитывает расстояние r = cτ до спутника. По расстояниям r1, r2, r3, r4 до трёх-четырёх спутников и по их координатам микроЭВМ рассчитывает положение приёмника на земной поверхности.
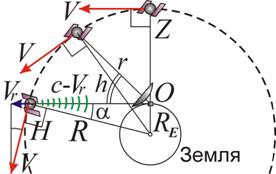
Рис. 6. Схема движения и радиолокации навигационных спутников Земли.
Полагают, что GPS и ГЛОНАСС подтверждают формулу r = cτ и постоянство скорости c сигналов от спутников [53]. Проверим, насколько этот вывод обоснован. Спутники выводят на орбиты радиуса R порядка 26000 км. Скорость спутников V ≈ 4 км/с снизит скорость их сигнала до c' = c – Vr, где Vr – лучевая скорость спутника для приёмника O. Тогда поправка расстояния Δ = rVr/c, где для спутника в зените Z скорость Vr = 0, но она растёт при уменьшении высоты h спутника над горизонтом: Vr = V·sinα·cosh, где sinα = RE/R ≈ 0,25, RE ≈ 6400 км – радиус Земли (рис. 6). Тогда максимальная ошибка дистанции Δ = rVr/c = 67 м у спутника возле горизонта H. Поскольку обычно приёмник «ловит» сигналы от спутников с h > 10° – 15° и располагается под углом θ > 0° к плоскости орбиты спутника, то Vr = V·sinα·cosh·cosθ, что, с учётом cosh ≤ 1, cosθ ≤ 1, даёт среднюю ошибку
![]() (7)
(7)
По сути, это ошибка в расстоянии до одного спутника, а расчёт координат ведут по 6–10 спутникам. Все они дают ошибки разных знаков и величин, случайно суммируемые в разных направлениях, и их взаимная компенсация при усреднении ещё сильней снижает ошибку. Причём это – общая ошибка по высоте и по горизонтали, а ошибка в измерении проекции на земной шар ещё ниже. В итоге, вносимая вариацией скорости света поправка к горизонтальным координатам приёмника – порядка 5 м, что сравнимо с наблюдаемыми ошибками. Причём, в согласии с формулой (7), фактически наблюдаемые ошибки Δ практически обращаются в нуль для спутников в зените (h = 90°), и растут при уменьшении их высот h, достигая максимума, когда спутник виден возле горизонта. Обычно это объясняют увеличением проходимого сигналом слоя атмосферы и ионосферы, меняющей скорость радиосигнала. Однако сравнение дистанций, измеренных при помощи радиосигналов, передаваемых на двух частотах (для которых скорости за счёт дисперсии в ионосфере несколько отличаются) обычно позволяет почти полностью исключить погрешности, связанные с рефракцией и дисперсией ионосферы. Поэтому порядок величины ошибок и их зависимость от высоты спутника может косвенно свидетельствовать в пользу влияния скорости спутника на скорость испущенных им радиосигналов.
Эти ошибки снижают, применяя корректирующие процедуры, в том числе дифференциальные методы с привязкой к базовым станциям. Систематические ошибки в измерении абсолютных расстояний r1 от спутника до мобильного приёмника и r2 – до расположенной поблизости базовой станции (с точно известными координатами), исчезают при определении относительного расстояния и положения приёмника как разности (r1 – r2), с учётом высоты спутника над горизонтом.
Кроме того, одну ошибку компенсируют другой, корректируя эфемериды спутников, «сдвигая» их вперёд по орбите на сотни метров (как в случае Венеры, условно сдвинутой на сотни км). Так, если координаты и эфемериды спутника рассчитаны по временам распространения его сигналов до базовых станций с известными координатами, то из постоянной скорости сигнала положение спутника получают смещённым от реального, что в точности скомпенсирует ошибку измерения расстояний до мобильных приёмников. Видимо, именно при таких условиях и считают, что GPS не противоречит СТО [53]. Поэтому для контроля положения спутников его следует независимо измерять разными методами: визуально (телескопами); лазерной локацией (по времени движения света к спутнику и обратно); радиолокацией (по временам движения радиосигнала от наземной станции к спутнику или от спутника к станции), а также с помощью радиоинтерферометров со сверхдлинной базой [54]. Тогда, в случае влияния скорости источника на скорость света, эти методы дадут разные результаты.
Для визуального анализа особенно удобны геостационарные спутники (иногда применяемые в качестве вспомогательных в навигационных системах), положение которых на небосводе практически не меняется, что позволяет очень точно измерять их положения. Сравнение этих положений с данными радаров и лазерной локации, а также сопоставление измеренной дистанции с теоретической высотой геостационарной орбиты (точно рассчитанной по орбитальному периоду, равному суткам), позволит выявить малейшие следы влияния орбитальной скорости спутника на скорость света. Об ошибках в системе GPS и противоречиях её данных – теории относительности неоднократно заявлял и Р. Хатч [60] – пионер разработок системы GPS, глава компании NavCom и Института систем космической навигации (ION).
Для проверки влияния скорости источника на скорость света можно применить не только навигационные, но и любые другие спутники и орбитальные станции, на борту которых обычно устанавливают уголковые отражатели и радио-ретрансляторы. Сравнение расстояний и положений аппаратов, одновременно измеренных разными методами, может стать простым и надёжным критерием проверки баллистической теории и постоянства скорости света. Также можно использовать возможности аппаратов типа спутника «Кондор» («Космос-2487»), положение которого на орбите точно контролируется и который с высокой точностью измеряет координаты наземных объектов. Отметим, что и при «стрельбе» со спутников лазерным лучом по наземным контрольным мишеням приходится учитывать баллистический принцип: без этого луч всегда уходит на несколько метров вперёд за счёт эффекта аберрации (то есть добавления вектора орбитальной скорости спутника к вектору скорости испущенного им светового луча).
Итак, проверка баллистической теории в космосе крайне актуальна, поскольку радарные ошибки от неучтённых вариаций скорости света могут снижать точность космических программ и вести к авариям космических кораблей, а также простых судов и автомашин с GPS. Однако постоянство скорости света в космосе до сих пор однозначно не проверено с использованием спутников, ракет и радаров, хотя вопрос о такой проверке неоднократно поднимался. Причём, когда в 1961 г. на конференции NASA в США этот вопрос был поставлен, такую проверку вообще сочли излишней [29], хотя в том же году неточности в скорости света дали о себе знать при радиолокации Венеры [5, 11, 12].
Американский физик Б. Уоллес связывал подобное замораживание официальных исследований и информации по данной тематике (в виде прекращения публикаций в США по радиолокации планет в 1960-х гг. [3]) – с развёртыванием программы «звёздных войн» (одним из пунктов которой была система GPS), где влияние скорости источника на скорость света могло представлять собой стратегически важную информацию [13, 36]. Нечто подобное имело место во время «Манхэттенского проекта», когда прекращение публикаций в 1940 г. по реакциям деления в американских журналах послужило сигналом о начале секретных работ в этой области, который советские физики правильно истолковали для начала своевременных разработок ядерного щита Родины.
4. Ошибки лазерной локации
Открыты неточности и при Лазерной Локации Луны (ЛЛЛ) и искусственных спутников, с установленными на их поверхности уголковыми отражателями [55]. При скорости лазерного источника порядка vr ≈ 460 м/с (скорость вращения на экваторе Земли) свет пройдёт расстояние r ≈ 3,84·108 м до Луны быстрее на время Δt = r/c – r/(c + vr) = rvr/c2 ≈ 2·10–6 с, что соответствует разнице в 600 м, легко измеримой лазерным радаром (лидаром). С учётом отражения от Луны на скорости c, ошибка составит Δr ≈ 300 м, при точности метода ~ 1 см [2]. Тогда при синхронном измерении расстояния Земля-Луна станциями из противоположных точек Земли, когда одна движется к Луне, а другая удаляется (рис. 7.а), баллистическая теория Ритца подтвердится в случае выявления разницы дистанций Δr ~ 300 м. Для станций умеренных широт разница меньше: Δr ~ 100 м.
Рис. 7. Схема лазерной локации Луны. Неучтённая вариация скорости света создаёт иллюзию сдвига или поворота Луны (а), Земли (б) и вариации суток (в).
Лазерную локацию может вести и одна станция, измеряющая расстояние Земля-Луна в течение ночи. Тогда невязки менялись бы с периодом в сутки со скоростью порядка 100 м/24 ч ≈ 4 м/ч, а предельное отклонение от истинного расстояния составило бы около ста метров. Действительно, невязки данных ЛЛЛ и визуальных данных (на основе которых рассчитаны эфемериды Луны) достигали сотни метров и менялись на величину порядка 4 м в час [56, с. 193]. Как показал сотрудник NASA Д. Джезари, изучив данные лазерной локации Луны, вариации систематических невязок противоречат постоянству скорости света, а учёт баллистического принципа заметно снижает эти вариации и систематические ошибки [55]. Напротив, в СТО расхождение данных ЛЛЛ с эфемеридами удаётся снизить лишь посредством коррекции эфемерид Луны на основе данных лазерной локации. По сути, локационные данные, как в случае Венеры, сравнивают друг с другом, а не с данными наблюдательной астрономии.
Считая скорость света константой, находят, что Луна на восходе ближе, чем на закате. Это неравенство расценят как поворот Земли в сторону вращения на лишний угол α = Δr/RE = 4,5·10–5 = 9'',4 (рис. 7.б) или как смещение уголкового отражателя с Луной на расстояние rα = 17 км вперёд по орбите (рис. 7.а). От наклона лунной орбиты к плоскости земного экватора расстояние r до Луны меняется на величину Δr ~ RE(1 – cos 23,5°) = 530 км с периодом в полмесяца (13,7 сут). Это меняет угол α на Δα = αΔr/r = 0'',013, что воспримут как покачивание Земли вокруг оси с амплитудой Δα/2 = 0'',0066 и периодом T ≈ 14 сут по закону
δα = -0'',0066·cos(2πt/T), (8)
где t отсчитывают от момента пересечения Луной экваториальной плоскости Земли (от восходящего узла). Это покачивание (8) создаёт иллюзию колебания скорости вращения Земли (ω = 2π рад/сут) на величину
δω = d(δα)/dt = 1,4·10–8·sin(2π/T) рад/сут, (9)
а длительности суток p – на величину δp = -pδω/ω, словно день то удлиняется, то укорачивается на 0,2 мс каждые 14 дней по закону
Эта теоретическая зависимость (10) нанесена сплошной линией на (рис. 7.в). Лазерная локация Луны выявила именно такие вариации (рис. 7.в, пунктир): их период – 14 суток, а амплитуда – доли миллисекунды [57].
Выходит, вариации p могут быть отчасти иллюзорны, будучи вызваны неучтённой вариацией скорости света. Это можно непосредственно проверить, проводя регулярные измерения угла поворота Земли и периода её вращения по наблюдениям суточного движения по небосводу точечных космических источников радиоизлучения, посредством радиоинтерферометров со сверхдлинной базой, позволяющих измерить вариации угла поворота Земли с точностью до 0'',0001. Другой способ проверки – измерение вариаций положений на небосводе геостационарных спутников. Или, напротив,– измерение со спутников типа «Кондор» вариаций положений земных реперов и базовых станций, для которых регулярные покачивания Земли на Δα = 0'',013 соответствовали бы периодичному смещению реперных точек по поверхности Земли примерно на ~ REΔα = 0,4 м.
Регулярные колебания дистанции r и скорости vr могли бы объяснить и другие «вариации» вращения Земли и Луны, выявленные лидарами и имеющие характерные периоды колебаний r и vr. Так, от движения по эллиптической орбите расстояние Луны меняется от 350 до 400 тыс. км (Δr ~ 50 тыс. км). Соответственно колеблется угол α (направления на мнимую Луну) на Δα = αΔr/r ~ 1''. Это колебание, синхронное с орбитальным движением, воспримется как «сдвиг» Луны по орбите (аналогичный «сдвигу» Венеры), меняющийся в такт её приближению-отдалению. Эти мнимые смещения нельзя вполне согласовать с законами Кеплера, т.к. форма и наклон лунной орбиты регулярно меняются [56, с. 63], внося дополнительную вариацию дистанции Земля-Луна Δr ~ 20 тыс. км и Δα = αΔr/r ~ 0'',5. Её могут интерпретировать как регулярное смещение уголкового отражателя на Δαr ~ 1 км в ходе покачиваний Луны (радиуса RM) на угол φ = Δαr/RM ~ 2'. Действительно, лидары выявили у Луны регулярные повороты на 2', в отличие от видимых качаний Луны (оптической либрации), объясняемые реальным покачиванием (физической либрацией).
«Покачивания» Луны и Земли за счёт приливных взаимодействий открыты на пределе разрешения и в астрономических наблюдениях [56, 58]. Однако «покачивания», выявленные лидарами, могут быть частично вызваны неучтённой вариацией скорости света. Проверить, насколько велик вклад мнимых колебаний, можно путём сравнения амплитуды «покачиваний» Луны или Земли, измеренной лидарами, телескопами и радиоинтерферометрами. Если баллистическая теория Ритца справедлива, их данные разойдутся на величину, меняющуюся по найденным законам. Будут расходиться и данные станций разных широт: возле экватора колебания δp – синусоидальные (10), а вдали от него – соседние максимумы будут получаться разной высоты, что реально наблюдается (рис. 7.в).
Ошибки в измеренных лидаром положениях Луны приводят и к ошибкам в координатах аппаратов на ней. Возможно, поэтому лазерный луч, по мере его заострения и засветки на Луне всё меньшей области (поперечник которой ныне сократился до величины порядка 1 км), и перестал со временем находить уголковый отражатель «Лунохода-1», ввиду ложного смещения на Δαr ~ 1 км от измеренной лидаром физической либрации, или на rα ~ 17 км – от вращения Земли. Действительно, после нескольких удачных сеансов лазерной локации «Лунохода-1» в 1970–1971 г. его уже не удавалось обнаружить лазерным радаром. Долгое время это связывали с выходом из строя установленного на «Луноходе» уголкового отражателя [2]. Однако в 2010 г., после того как «Луноход-1» был визуально обнаружен на снимках поверхности Луны, сделанным лунным орбитальным зондом LRO [59], координаты «Лунохода-1» были уточнены по визуальным данным и снимкам. Использование этих исправленных координат позволило, спустя 40 лет, вновь точно навести лазерный луч на «Луноход-1» и зарегистрировать «лунный зайчик» – отражённый сигнал. Причём его интенсивность в несколько раз превышала интенсивность сигнала, отражённого «Луноходом-2» [59], лазерная локация которого регулярно поддерживалась до настоящего времени, и координаты которого не были потеряны, благодаря визуальному контролю (измерению координат вспыхивающей точки на Луне).
Это доказывает, что уголковый отражатель «Лунохода-1» всё время был исправен, а исчезновение отражённого сигнала было связано с потерей правильных координат аппарата, из-за ошибки в определении координат «Лунохода-1» по данным лидаров, по сравнению с которыми визуальные данные в ряде случаев оказываются точнее. Возможно, с этим связана и постепенная «деградация» (снижение отражательной способности) отражателей других четырёх лунных аппаратов [59],– из-за постепенной потери правильных координат в отражатели попадает только край рассеянного атмосферой и дифракцией лазерного пучка, с пониженной интенсивностью, отчего и падает интенсивность отражённого сигнала. В итоге регулярно «теряются» и отражатели других четырёх лунных аппаратов, включая «Луноход-2». Лишь первоначальное визуальное измерение положений отражателей (или современные измерения – с помощью орбитальных зондов типа LRO) дают требуемую точность измерения их координат.
Действительно, сравнение координат всех пяти уголковых отражателей лунных аппаратов («Луноход-1, 2», «Аполлон-11, 14, 15»), определённых по визуальным данным (по снимкам LRO) и по данным лазерной локации, показывают систематическое расхождение по селенографическим широтам и долготам порядка 0°,02 ≈ 1'. Это соотносится с характерной амплитудой физической либрации Луны (найденной из данных лидаров) и соответствует разнице координат в ~ 1 км. Это расхождение намного превышает точность измерения координат обоими методами и вполне может быть результатом неучтённого влияния скорости источника на скорость света в расчётах по данным лазерной локации.
5. Выводы
Как было показано выше, данные радиолокации и лазерной локации могут содержать большие систематические ошибки, связанные с неточностью принятого значения скорости света c. В итоге, хотя соседние относительные положения тел или аппаратов измеряются с высокой точностью и хорошей воспроизводимостью, координаты абсолютных положений и дистанций от Земли измеряются с большой погрешностью, превышающей погрешность визуальных угломерных измерений. Учёт влияния скорости источника на скорость света и радиосигналов позволяет существенно снизить систематические ошибки. Проверить это влияние можно при сопоставлении данных радио- и лазерной локации с данными интерферометрических измерений на базе телескопов и радиотелескопов со сверхдлинной базой, у которых точность измерения, выраженная в линейной мере, уже приближается к точности дальномерных измерений, позволяя произвести независимые и точные замеры. Таким образом, если прежде предпочтение всегда отдавалось дальномерным измерениям, то теперь точность и случайные ошибки дальномерных и угломерных измерений стали сопоставимы, что позволяет непосредственно сравнивать данные этих методов и выявлять наличие систематических ошибок.
Итак, новый анализ массива данных радиолокации и лазерной локации, сопоставление их между собой, с визуальными данными и с данными расчётных положений планет или АМС позволит проверить постоянство скорости света в космосе и уточнить параметры осевого и орбитального вращения планет и Луны. А в действующих программах параллельное вычисление координат на базе баллистической теории и на базе постоянства скорости света позволит сравнить точность этих процедур расчёта и повысить надёжность космической навигации. В перспективе это позволит создать интеллектуальные системы навигации, в которых координаты будут параллельно и независимо измеряться разными методами и сопоставляться с учётом влияния скорости источника на скорость света и с учётом переменной толщины и концентрации межпланетной среды, ведущей к переизлучению сигнала и к изменению его скорости.
Выражаю благодарность за обсуждение М.И. Бакунову, Н.Ф. Андрееву, С.А. Гилёву и А.Э. Рассадину. Работа выполнена в рамках программы развития «ННГУ – НИУ». Результаты работы доложены на 1-й Российско-белорусской научно-технической конференции «Элементная база отечественной радиоэлектроники», посвящённой 110-летию со дня рождения О.В. Лосева, Нижний Новгород, 11-14 сентября 2013 г. [61].
Литература
1. Петров Г.М. Радиолокационные исследования Венеры // Земля и Вселенная. 1982. № 1. С. 8–16.
2. Алёшкина Е.Ю. Лазерная локация Луны // Природа. 2002. №9. С. 57–66.
3. Красинский Г.А., Питьева Е.В., Свешников М.Л., Свешникова Е.С. Некоторые результаты обработки радиолокационных, лазерных и оптических наблюдений внутренних планет и Луны // Докл. АН СССР. 1981. Т. 261. №6. С. 1320–1324.
4. Крюков П.Г. Фемтосекундные импульсы. М.: Физматлит, 2008. 208 с.
5. Фундаментальные постоянные астрономии. М.: Мир, 1967. 382 с.
6. Семиков С.А. // Инженер. 2014. №1. С. 36–40.
7. Андерсон Дж., Лаинг Ф., Лау Э., Ньето М., Туришев С. Странное ускорение «Пионеров» // Земля и Вселенная. 2002. №5. С. 78–81.
8. Селезнёв В.П. Космический навигатор // Наука и религия. 1998. №5-6. С. 26–29.
9. Дёмин В.Н., Селезнёв В.П. Мироздание постигая. М.: Молодая гвардия, 1989. 267 с.
10. Дёмин В.Н., Селезнёв В.П. К звёздам быстрее света: русский космизм вчера, сегодня, завтра. М.: УРСС, 2011. 432 с.
11. Wallace B.G. Radar Testing of the Relative Velocity of Light in Space // Spectroscopy Letters. 1969. V. 2. P. 361–367.
12. Wallace B.G. Radar Evidence that the Velocity of Light in Space is not c // Spectroscopy Letters. 1971. V. 4. P. 79–84.
13. Уоллес Б. Проблема пространства и времени в современной физике // Сборник "Проблемы исследования Вселенной", вып. 15. Проблемы пространства и времени в современном естествознании. СПб., 1991. с. 258–267.
14. Шапиро И. Радиолокационные наблюдения планет // УФН. 1969. Т. 99. С. 319–336.
15. Семиков С.А. Об экспериментальной проверке баллистической теории света // Вестник ННГУ. 2013. №4. С. 56–63.
16. Семиков С.А. Преобразование электромагнитных волн в поле ускорений // В кн.: Труды XIV-й научной конференции по радиофизике. 7 мая 2010 г. /Ред. А.В. Якимов, С.М. Грач. – Н. Новгород: Изд-во ННГУ, 2010. С. 188–190.
17. Семиков С.А. Генерация высоких гармоник при модуляции скорости источника // В кн.: Труды XVII-й научной конференции по радиофизике. 13–17 мая 2013 г. /Ред. А.В. Якимов, С.М. Грач. – Н. Новгород: Изд-во ННГУ, 2013. С. 153–155.
18. Дуплищева О.М., Дуплищев А.М. Михаил Илларионович Дуплищев. Теоретические и экспериментальные исследования явлений излучения и распространения света в пространстве. Днепропетровск: АРТ-ПРЕСС, 2012, 352 с.
19. Дуплищева О.М., Дуплищев А.М. Наставник инженеров и учёных. Днепропетровск: АРТ-ПРЕСС, 2007. 232 с.
20. Толчельникова-Мури С.А. Радарные наблюдения Венеры как практическая проверка СТО // Известия ВУЗов. Геодезия и аэрофотосъёмка. 2001. №6. С. 85–108.
21. Мушаилов Б.Р., Теплицкая В.С. О надёжности определения орбитальных параметров экзопланет доплеровским методом // Космические исследования. 2012. №6. С. 452–461.
22. Мушаилов Б.Р., Теплицкая В.С. Спектрометрический метод обнаружения экзопланет как ещё один тест для проверки инвариантности скорости света // Вестник МГУ, серия 3. 2011. №6. С. 98–103.
23. Семиков С.А. Экзопланетная экзотика: иллюзии и реальность // Техника-молодёжи. 2013. №1. С. 24–26.
24. De Sitter W. // Phys. Z. 1913. Bd. 14. S. 429, 1267.
25. Guthnick P. // Astr. Nachr. 1913. Bd. 195. S. 265–270.
26. Freundlich E. // Phys. Z. 1913. Bd. 14. S. 835–838.
27. Роузвер Н.Т. Перигелий Меркурия от Леверье до Эйнштейна. М.: Мир, 1985. С. 161.
28. Fox J.G. Evidence Against Emission Theories // Am. J. Phys. 1965. V. 33. P. 1–17.
29.Франкфурт У.И. Специальная и общая теория относительности. М.: Наука, 1968. 332 с.
30. Франкфурт У.И., Френк А.М. Оптика движущихся тел. М.: Наука, 1972. 212 с.
31. Сацункевич И.С. Экспериментальные корни специальной теории относительности. М.: УРСС, 2003. 176 с.
32. Котельников В.А., Дубровин В.М., Морозов В.А. и др. Результаты радиолокации Венеры в 1961 г. // Радиотехника и электроника. 1962. Т. 7. №11. С. 1860–1872.
33. Котельников В.А., Аким Э.Л., Александров Ю.Н. и др. Измерения времени запаздывания и доплеровской поправки в радиолокационных наблюдениях Венеры в 1975 г. // Астрономический журнал. 1976. Т. 53. № 6. С. 1270–1277.
34. Котельников В.А., Дубровин В.М., Дубинский Б.А. и др. Радиолокационные наблюдения Венеры в Советском Союзе в 1962 году // Докл. АН СССР. 1963. Т. 151. № 3. С. 532–535.
35. Шурупов А.К. Радиолокация Венеры // Журнал научно-физического кружка им. М.В. Ломоносова. 1970. №8. март.
36. Секерин В.И. Теория относительности – мистификация века. Новосибирск, 1991. 56 с.
37. Котельников В.А., Дубровин В.М., Кузнецов Б.И. и др. Успехи планетной радиолокации // Природа. 1964. №9. С. 2–12.
38. Котельников В.А., Александров Ю.Н., Апраксин Л.В. и др. // Докл. АН СССР. 1965. Т. 163. № 1. С. 50–53.
39. Кислик М.Д., Колюка Ю.Ф., Котельников В.А. и др. Определение орбит Земли и Венеры, астрономической единицы и радиуса Венеры на основе радиолокационных наблюдений Венеры в 1962-1977 гг. // Докл. АН СССР. 1978. Т. 241. №5. С. 1046–1049.
40. Кислик М.Д., Колюка Ю.Ф., Котельников В.А. и др. Единая релятивистская теория движения внутренних планет Солнечной системы // Докл. АН СССР. 1980. Т. 255. №3. С. 545–547.
41. Прохождение Венеры по диску Солнца 8 июня 2004 г.: Наблюдения на Астрополигоне НИИФТРИ // [Электронный ресурс]. URL: http://astroclub-irk.narod.ru/Astroclub/Observations/TransitOfVenus20040608/TransitOfVenus20040608_r.html
42. Леушканов А. Планета, которая всех обманула // Русский Север. 9 июня 2004 г. С. 8.
43. Ходж П. Революция в астрономии. М.: Мир, 1972. С. 19.
44. Александров Ю.Н., Вышлов А.С., Дубровин В.М. и др. Радиолокационные наблюдения Марса, Венеры и Меркурия на волне 39 см в 1980 г. // Докл. АН СССР. 1980. Т. 255. №6. С. 1334–1338.
45. Аким Э.Л., Степаньянц В.А. Численная теория движения Земли и Венеры по данным радиолокационных, оптических наблюдений и наблюдений за движением искусственных спутников «Венера-9» и «Венера-10» // Докл. АН СССР. 1977. Т. 233. №3. С. 314–317.
46. Селезнёва Н.В. Покорение космического пространства: эпопеи советского изобретателя. М.: Либроком, 2013. 360 с.
47. Семиков С.А. Баллистическая теория Ритца и картина мироздания. Н. Новгород: Стимул-СТ, 2010. 612 с.
48. Anderson J.D., Nieto M.M. Astrometric Solar-System Anomalies // [Электронный ресурс]. URL: http://arxiv.org/pdf/0907.2469v2.pdf
49. Anderson J.D., Laing P.A., Lau E.L., et al. Indication, from Pioneer 10/11, Galileo, and Ulysses Data, of an Apparent Anomalous, Weak, Long-Range Acceleration // Phys. Rev. Lett. 1998. V. 81. P. 2858–2861.
50. Anderson J.D., Lau E.L., Giampieri G. Improved Test of General Relativity with Radio Doppler Data from the Cassini Spacecraft // [Электронный ресурс]. URL: http://arxiv.org/abs/gr-qc/0308010v1.pdf
51. Turyshev S.G., Toth V.T., Kinsella G., et al. Support for the thermal origin of the Pioneer anomaly // Phys. Rev. Lett. 2012. V. 108. P. 241101–241105.
52. Семиков С.А. Справедливость баллистической теории в радиолокации // Инженер. 2010. №10. С. 6–8.
53. Van Flandern T. What the Global Positioning System Tells Us about Relativity // From the book «Open Questions in Relativistic Physics». Monreal: Apeiron, 1998. P. 81–90.
54. Дугин Н.А., Гавриленко В.Г., Нечаева М.Б. и др. РСДБ-эксперименты по приёму сигналов навигационных космических аппаратов // В кн.: Труды XVI-й научной конференции по радиофизике. 11–18 мая 2012 г. /Ред. С.М. Грач, А.В. Якимов. – Н. Новгород: Изд-во ННГУ, 2012. C. 66–67.
55. Gezari D.Y. Lunar Laser Ranging Test of the Invariance of c // [Электронный ресурс]. URL: http://arxiv.org/abs/0912.3934
56. Бронштэн В.А. Как движется Луна? М.: Наука, 1990. 208 с.
57. Сидоренков Н.С. // Вестник РАН. 2004. Т. 74. № 8. С. 701–715.
58. Горыня А.А. Постоянные физической либрации Луны. Киев: Наукова думка, 1969. 276 с.
59. Murphy T.W., Adelberger E.G., Battat J.B.R., et al. Laser ranging to the lost Lunokhod 1 reflector // Icarus. 2011. V. 211. P. 1103–1108.
60. Hatch R.R. Relativity and GPS // Galilean Electrodynamics. 1995. V. 6. N3-4. P. 51–57.
61. Семиков С.А. О возможных источниках вычислительных ошибок космической навигации, GPS и ГЛОНАСС, лазерной локации и радиолокации // Труды 1-й российско-белорусской научно-технической конференции «Элементная база отечественной радиоэлектроники», посвящённой 110-ю со дня рождения О.В. Лосева / Под ред. А.Э. Рассадина. – Н. Новгород.: НИЖЕГОРОДСКАЯ РАДИОЛАБОРАТОРИЯ. 2013. В 2-х т. Т. 1. С. 236-240.