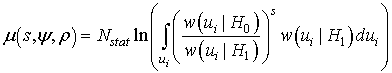"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 12, 2014

оглавление

УДК 778.38: 615.071

АНАЛИЗ ОСОБЕННОСТЕЙ ИСПОЛЬЗОВАНИЯ ФАЗОВОЙ И АМПЛИТУДНОЙ ФУНКЦИЙ БЛИЗОСТИ В ЗАДАЧАХ ЭТАЛОННОЙ ОЦЕНКИ ПАРАМЕТРОВ ОБЪЕКТОВ В РАДИОГОЛОГРАФИИ

 

А. С. Гвоздарёв, Т. К. Артёмова, К. С. Артёмов

Ярославский государственный  университет им. П.Г. Демидова

Статья получена 27 ноября 2014 г.

 

Аннотация. В работе рассмотрена задача выбора минимального шага сетки эталонов (минимального расстояния между ними) при формировании набора эталонных объектов для проведения эталонного оценивания параметров радиоголографических объектов. В качестве мер близости между исследуемым объектом и эталоном использовались расстояние Евклида (амплитудный критерий) и интегральная разность фаз (фазовый критерий. Исследована зависимость выигрыша одной функции близости перед другой по величине отношения сигнал/шум, требуемой для достижения заданной вероятности верной классификации, от размеров (числа пространственных дискретов или числа элементов антенной решётки, регистрирующей радиоголограмму) эталонных радиоголограмм и угла раскрыва апертуры. Указаны диапазоны изменения параметров, при которых он может быть достигнут.

Ключевые слова: оценка параметров, система голографического радиовидения, эталонный метод, интегральная разность фаз, расстояние Евклида.

Abstract. Euclidean distance and integral phase difference criteria used for reference set construction are analyzed. The potential gain in signal-to-noise ratio, needed for a given detection probability is studied for various parameters such as antenna element number and aperture angular size. The parameter's range when the gain is obtained is analyzed.  Guidelines for design process of the holographic system exploiting minimum-phase method are proposed.

Key words: parameter estimation, radioholographic system, reference set method, integral phase difference, Euclid distance.

 

Введение

Одной из наиболее важных задач, возникающих при формировании набора (базы) эталонов для проведения эталонной оценки параметров объектов [1–2] в системах голографического радиовидения (СГРВ) [3–4] является задача выбора минимального шага сетки эталонов.

С одной стороны, нецелесообразно выбирать большой шаг, больший решающей способности СГРВ по величине оцениваемого параметра. Это накладывает ограничение на минимальный шаг сверху. С другой стороны, на примере минимально-фазового метода (МФМ), использующего в качестве критерия принятия решения минимум интегральной разности фаз (ИРФ), авторами в работах [5–6] было показано, что решение этой задачи может быть получено путём введения ограничений на допустимую вероятность правильной классификации PD или вероятность ошибочной классификации Pε  двух соседних эталонов. Таким образом, вероятность различения двух ближайших эталонов при сравнении с одним и тем же объектом в условиях наличия шумов и помех накладывает ограничение на шаг снизу. Таким образом, на практике приходится искать компромиссное решение в интервале между этими двумя граничными значениями.

Важно отметить, что решение задачи выбора минимального шага сетки будет зависеть от того, какое правило принятия решения о выборе наиболее подходящего эталона (функция близости) заложено в сам метод [7]. Во многих практических приложениях (см., например, [7]) в качестве правила принятия решения используется классическая евклидова функция близости, однако сетка эталонов специальным образом не оптимизируется. В то же время, как было отмечено в [6], за счёт повышения соотношения сигнал/шум (ОСШ) q при прочих фиксированных условиях можно достичь любой конечной разрешающей способности эталонного метода и с использованием ИРФ.

Поскольку на практике требование обеспечения высокого ОСШ накладывает достаточно жёсткие ограничения на систему в целом, то разумно пытаться понизить минимальную величину ОСШ, обеспечивающую достижение заданного уровня PD, за счёт выбора в конкретных условиях определённой функции близости.

Настоящее исследование посвящено анализу поведения амплитудной (на примере расстояния Евклида) и фазовой (на примере ИРФ) функций близости при формировании набора опорных радиоголограмм на основе введения ограничений на PD в задачах эталонной оценки параметров радиоголографических объектов.

1. Общий подход к эталонному оцениванию в СГРВ

Рассмотрим общий подход к эталонному оцениванию параметров радиоголографических объектов.

Пусть при неизменных за время регистрации радиоголограммы характеристиках СГРВ (размер и тип апертуры, способ формирования зондирующего и опорного сигналов и  регистрации поля, рассеянного объектом, и др.) исследуемый объект облучается зондирующим сигналом с известными параметрами (форма сигнала, рабочая частота, полоса перестройки частоты, поляризационные характеристики и др.). Без потери общности предположим для удобства, что зондирующий сигнал – гармонический. Тогда на некоторой частоте радиоголограмма или поле, рассеянное объектом с параметром (или совокупностью параметров) R, в некоторой отсчётной точке на апертуре, характеризующейся направлением α, имеет комплексную амплитуду .

Пусть при помощи -элементной антенной решётки осуществляется дискретная в пространстве регистрация поля , рассеянного исследуемым объектом с оцениваемым параметром , причём известны координаты антенн – конечный набор  из диапазона . В месте расположения каждой антенны при фиксированном значении параметра  для наблюдения в результате накопления доступно  реализаций . Будем в дальнейшем считать, что приёмная часть СГРВ регистрирует поле, рассеянное исследуемым объектом, в присутствии комплексного аддитивного белого гауссового шума с дисперсией   . Пусть для ряда  значений оцениваемого параметра  (сетки эталонов) в отсутствие шумов (или в условиях пренебрежимо малого уровня шумов) заранее сформирован набор опорных (эталонных) радиоголограмм .

Тогда задача поиска оценки   параметра  сводится к ассоциированию регистрируемой выборки с одним из эталонов в соответствии с некоторой функцией близости, указывающей степень "сходства" объекта и эталона. По  наблюдениям производится оценка этой функции и выбирается тот из эталонов, который обеспечивает её минимум.

На практике чаще всего в качестве меры близости выбирают евклидово расстояние  , с другой стороны, в работах [5–6] было показано, что для решения подобной задачи может быть выбрана интегральная разность фаз .

Тогда в качестве оценки исследуемого параметра  выбирается значение эталонного параметра , минимизирующее величину  или , т.е.:  или   .

Таким образом, задаваясь амплитудным или фазовым правилом принятия решения, задачу формирования набора опорных (эталонных) радиоголограмм, т.е. выбора минимального шага сетки эталонов можно решить, действуя в соответствии со следующим алгоритмом.

1.  Для заданной статистическо-вероятностной модели шумов/помех определить распределение выбранной функции близости.

2.  Для двух произвольно выбранных эталонов сформулировать задачу проверки гипотезы о том, что системой обработки они будут различены, против альтернативы, что они будут неразличимы.

3.  Вводя ограничения на допустимую величину PD, определить минимальную разницу в значении оцениваемого параметра  – шаг эталонной сетки.

2. Построение классификационной сетки эталонов на основе PD

Для оценки вероятности верной классификации двух соседних эталонов PD воспользуемся подходом, рассмотренным авторами в работах [5–6], который сводит задачу оценки параметра объекта к задаче проверки гипотезы:

                                            (1)            

где  – производящая функция моментов функционала отношения правдоподобия:

         (2)

для случая задачи проверки простой гипотезы H0 (о том, что два выбранных эталона различимы) против сложной альтернативы H1 (о том, что два выбранных эталона неразличимы),  – апостериорная плотность вероятности по гипотезе H0 или H1, а  вычисляется в предположении, что ошибки первого и второго рода для рассматриваемой задачи  равноправны, т.е. при .  

При вычислении (2) для фазового критерия использовалось выражение для плотности распределения вероятности ИРФ, полученное авторами ранее [8]:

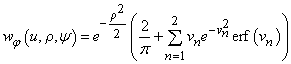                              ,                         (3)                        

где , – функция ошибок,  – есть истинное значение интегральной разности фаз в отсутствие шумов,  – коэффициент, равный произведению отношения сигнал/шум q и коэффициента амплитудного расхождения  [4].

Для случая амплитудного критерия было учтено, что евклидово расстояние подчиняется нецентральному хи-квадрат распределению:  с  числом степеней свободы , равным удвоенному количеству пространственных дискретов радиоголограммы (антенных элементов) , и параметром нецентральности , равным евклидову расстоянию между двумя рассматриваемыми эталонами в отсутствие шумов [8].

Исходя из введённых обозначений, можно сформулировать задачу проверки гипотезы о различимости двух выбранных эталонов следующим образом:

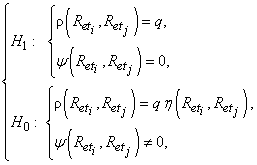    или       

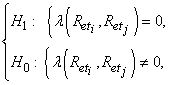
Величина минимального шага определялась как расстояние между двумя эталонами, для которых PD была не менее некоторой заданной величины. Важно также отметить, что в отсутствие шумов возможна реализация сколь угодно малого шага сетки эталонов и, как следствие, в реальной обстановке его величина во многом определяется значением ОСШ. Также факторами, влияющими на выбор минимального шага, являются геометрические размеры, форма объекта и его электродинамические характеристики (т.к. регистрируемое поле определяется решением задачи дифракции на нём), параметры СГРВ (количество антенных элементов, размер апертуры, диапазон углов анализа, объём статистической выборки, доступной для усреднения и др.).

3. Параметры моделей

Так как функции плотности вероятности критериев близости определяются конкретными объектами, то невозможно проводить анализ особенностей их использования без указания объекта исследования. Поэтому анализ будем проводить с использованием математического моделирования.

Для сравнения поведения функций близости были выбраны бесконечные идеально проводящие ленты, которые часто используются в качестве тестовых радиоголографических моделей реальных объектов, например, при определении разрешающей способности СГРВ, т.к. для них существуют аналитические решения задачи рассеяния [9].

Использовалась модель СГРВ с рабочей диной волны λ = 0.008 м, дуговой апертурой с углом раскрыва от 1º до 20º с шагом  0.2º и радиусом кривизны 21.2 м, количеством пространственных дискретов радиоголограммы (антенных элементов) от 5 до 100 с шагом 1. Расстояние между объектом и центром СГРВ 21.2 м. Теоретическая аппаратная разрешающая способность системы в такой конфигурации составляет 15 λ. Соотношение сигнал-шум изменялось в диапазоне от 10 до 50 дБ с шагом 0.2 дБ. Объём выборки для усреднения в каждой точке апертуры  составлял 5000 отсчётов.

Поля тестовых объектов записывались в присутствии шума, моделируемого комплексным АБГШ с нулевыми математическими ожиданиями и уровнями дисперсии синфазной и квадратурной компонент, определяемыми, исходя из требуемой величины отношения сигнал/шум, а для эталонных – без шума.

 

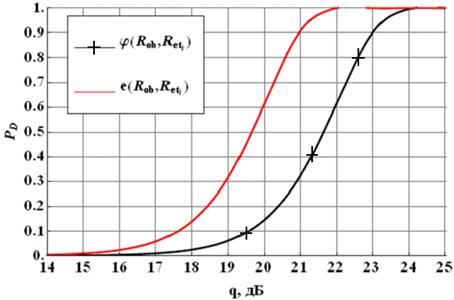
Рис. 1. Зависимость PD от q при Nα=11,  α=10°

 

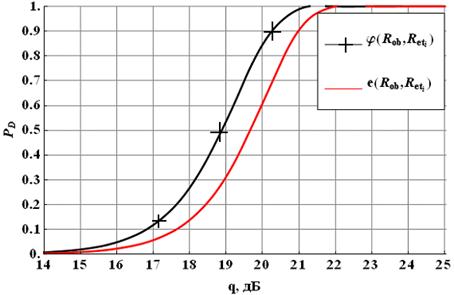
Рис. 2. Зависимость PD от q при Nα=21,  α=10°

 

На рисунках 1 и 2 для примера представлены зависимости PD от ОСШ q для двух рассматриваемых функций близости, угла раскрыва апертуры в 10° и 11 или 21 антенного элемента соответственно.

Анализируя полученные результаты, можно отметить, что при фиксированном ОСШ существуют области значений параметров СРГВ, для  которых использование фазового критерия оказывается преимущественным с точки зрения возможности достижения большей PD.

Таким образом, при сравнении поведения амплитудной (евклидовой) и фазовой (ИРФ) функций близости при формировании набора опорных радиоголограмм разумно учитывать влияние, которое оказывают различные факторы на выбор минимального шага сетки.

На рисунке 3 представлены графики зависимости величины ОСШ, необходимого для достижения заданного , от величины угла раскрыва приёмной апертуры (в градусах) для случая 10 пространственных отсчётов радиоголограммы (числа антенных элементов) при использовании расстояния Евклида   и ИРФ . Минимальный уровень PD при этом был выбран равным 0.99.

 

 

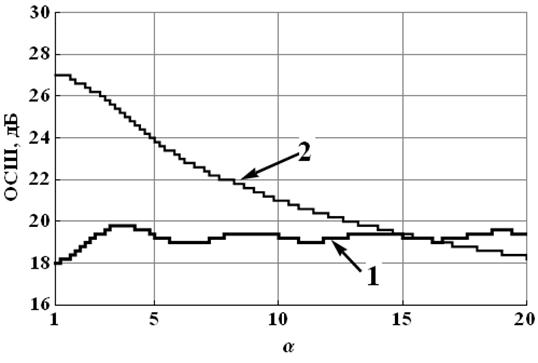
Рис. 3.  Зависимость величины ОСШ, необходимого для достижения заданного , от величины угла раскрыва приёмной апертуры для случая : 1 – амплитудная метрика (расстояние Евклида), 2 – фазовая метрика (ИРФ)

 

На основе анализа полученных результатов можно сделать заключение, что величина необходимого ОСШ для случая использования амплитудной метрики крайне слабо зависит от угла раскрыва антенной системы СГРВ. Так, например, при = 10 и > 5 требуемое ОСШ колеблется в диапазоне от 18.4 до 18.8 дБ, при шаге 0.2 дБ. Однако уже при  = 50, зависимость полностью исчезает и требуемое ОСШ постоянно во всём выбранном для анализа диапазоне изменения  и равно 22.8 дБ, а для = 100 также постоянно и равно 23.8 дБ. Для ИРФ наоборот обнаруживается явная зависимость уменьшения требуемого ОСШ с увеличением . При этом увеличение  с 10 до 50 и с 10 до 100 общее смещение графика незначительно и находится в пределах 0.2 – 0.6 дБ, что частично можно отнести к вычислительным погрешностям используемых алгоритмов численного интегрирования в (2).

4. Сравнение поведения расстояния Евклида  и ИРФ при выборе минимального шага сетки

В работах [5–6] на примере ИРФ был проведён подробный анализ зависимостей величины минимального шага эталонной сетки от таких параметров, как объём статистической выборки, истинное значение ИРФ, ОСШ и др. Однако с точки зрения практической реализации СГРВ, использующей эталонные методы оценки, основной интерес представляет зависимость минимального шага сетки от ОСШ. Поэтому далее будем сравнивать результаты, полученные с применением амплитудного и фазового критериев, по величине отношения сигнал/шум, необходимого для достижения желаемого уровня PD (обоими критериями) при заданной конфигурации системы, и по выигрышу по ОСШ (т.е. по разности ).

Анализируя полученные результаты, отметим, что весь диапазон изменения выбранного параметра можно условно разбить на участки, где та или иная функция близости даёт выигрыш в величине ОСШ, требуемого для достижения желаемой PD. При  , т.е. для обеспечения заданной точности оценки использование амплитудной метрики потребует меньшего ОСШ, при  использование ИФР даёт преимущество.

 

 

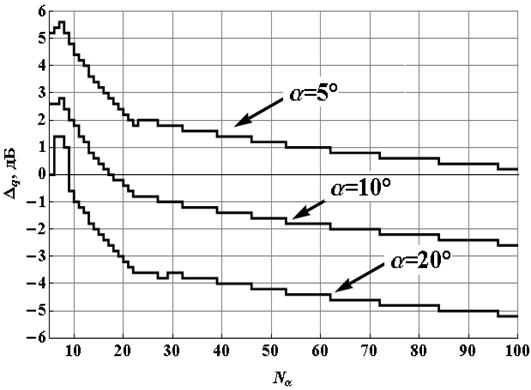
Рис. 4. Зависимость Δq от числа пространственных отсчётов радиоголограммы

 

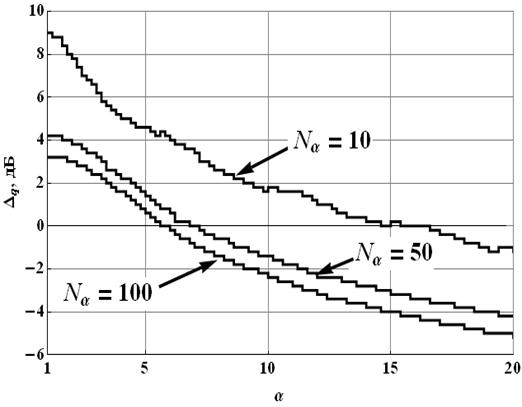
Рис. 5. Зависимость Δq от угла раскрыва приёмной апертуры СГРВ

 

На рисунках 4 и 5 изображены графики зависимостей выигрыша Δq амплитудной функции близости над фазовой по величине ОСШ от числа пространственных отсчётов радиоголограммы (числа антенных элементов) для трёх значений угла раскрыва приёмной апертуры (см. рисунок 4) и от угла раскрыва приёмной апертуры для трёх значений  (см. рисунок 5).

Анализ результатов моделирования позволяет сделать следующие выводы относительно поведения амплитудной и фазовой функций близости:

1.       для случая малых (до 5º) раскрывов при фиксировании угла раскрыва апертуры СГРВ увеличение числа антенных элементов позволяет минимизировать проигрыш (см. рисунок 5) фазовой функции близости по величине ОСШ, требуемого для достижения желаемого уровня PD и достичь равенства ОСШ при использовании  от 95 до 100 (для );

2.       для случая  при  элементов амплитудная функция близости проигрывает фазовой;

3.       для широкоапертурных многоэлементных СГРВ ( и ) выигрыш фазовой функции близости над амплитудной в ОСШ потенциально может достигать 5.2 дБ;

4.       скорость роста выигрыша максимальна при увеличении числа пространственных дискретов радиоголограммы (числа антенных элементов) с 10 до 20;

5.       при фиксировании  увеличение в 2 раза α (например, с 5º до 10º и с 10º до 20º) позволяет улучшить выигрыш фазовой функции близости над амплитудной в ОСШ на величину порядка 3 дБ;

6.       при фиксировании α пятикратное увеличение  (например, с 10 до 50) позволяет улучшить выигрыш фазовой функции близости над амплитудной в ОСШ порядка 3 дБ, при этом дальнейшее увеличение с 50 до 100 – лишь на 1 дБ.

Выводы            

С практической точки зрения реализация СГРВ с малой (до 5º) и малым числом антенных элементов (т.е. диапазоном параметров, при котором амплитудная функция близости даёт выигрыш по ОСШ) в микроволновом диапазоне не реалистична из-за крайне низкой разрешающей способности. В остальных случаях использование фазовой функции близости для построения системы эталонной оценки параметров позволяет снизить требования, предъявляемые для получения заданной PD, на величину вплоть до 5.2 дБ.

Полученные результаты могут быть использованы при проектировании СГРВ для определения наилучшего для данных условий (числа дискретов радиоголограммы (антенных элементов), углового раскрыва аппретуры, ОСШ, требуемой вероятности правильной классификации и т.д.) эталонного метода оценки параметров исследуемого объекта.

 

Литература

1.     Soulez F., Denis L., Fournier C., Thiebaut E., and Goepfert C. Inverse-problem approach for numerical suppression of the twin-image particle digital holography: accurate location based on local optimization // Journal of Optic Society of America (A). – 2007. – № 24(4). – P. 1164–1171.

2.     Bennett C., Toomey J. Target classification with multiple frequency illumination // IEEE Transactions on Antennas and Propagation. – 1981. – Vol. 29. – №2. – Pp. 352 – 358.

3.     Гончаров О. П., Понькин В.А. Пат. 2498339 Российская Федерация, МПК G01S13/00. Способ активной радиолокации / Гончаров О. П.,; заявитель и патентообладатель Гончаров О. П. (RU). – № 2012107869/07; заявл. 01.03.2012; опубл. 10.11.2013, Бюл. № 31. – 14 с.

4.     Артёмова Т.К., Гвоздарёв А.С. Минимально-фазовый метод эталонной оценки размеров объектов в задачах радиоголографии // Известия высших учебных заведений. Радиоэлектроника. – 2011. – T. 54, N 4. – С. 22 – 30.

5.     Гвоздарёв А.С., Артёмова Т.К., Артёмов К.С. Использование границы Чернова и статистического предела разрешения для определения точности оценки параметров радиоголографических объектов минимально-фазовым методом и построения классификационной сетки эталонов метода решётки [Электронный ресурс] // Журнал радиоэлектроники. – Декабрь 2012. – №12. – Режим доступа: http://jre.cplire.ru/jre/dec12/11/text.pdf

6.     Гвоздарёв А.С., Артёмова Т.К., Артёмов К.С. Анализ границ качества минимально-фазового метода эталонной оценки параметров объектов по радиоголограмме // Труды XVIII международной научно-технической конференции «Радиолокация, навигация, связь». – Воронеж, 2012. – Т. 1. – С. 168–177.

7.     Губарев В.В. Алгоритмы статистических измерений. – М.: Энергоатомиздат, 1985. 272 с.

8.     Гвоздарёв А.С., Артёмова Т.К., Артёмов К.С. Сравнение поведения амплитудной и фазовой метрик при формировании набора опорных радиоголограмм в задачах эталонной оценки параметров радиоголографических объектов // Труды XX международной научно-технической конференции «Радиолокация, навигация, связь». – Воронеж, 2014. – Т. 1. – С. 152–162.

9.     Уфимцев П. Я. Метод краевых волн в физической теории дифракции. – М.: Сов. радио, 1962. –  244 с.