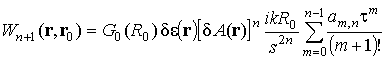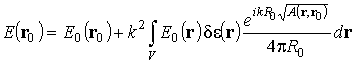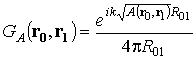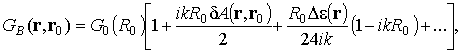УДК 537.876

Метод итерированных ядер в задачах распространения волн в неоднородных средах

 

Д. В. Лосев, Д. С. Бардашов

Томский государственный университет

Статья получена 8 декабря 2014 г.

Аннотация. Предложено приближенное решение задачи распространения волн в плавно-неоднородной среде на основе использования метода итерированных ядер. Оно представляет собой результат применения метода последовательных приближений к интегральному уравнению, эквивалентному скалярному уравнению Гельмгольца. Итоговое решение имеет компактный вид и объединяет в себе достоинства борновского рассеяния и коротковолновых асимптотических методов.

Ключевые слова: распространение волн, метод итерированных ядер.

Abstract: The approximated solution of waves propagation problem in smooth heterogeneous media by use of the iteratived kernels method is proposed. It represents the result of application of iteratived method to the integral equation equivalent to the Helmholtz scalar equation. The resulting decision has a compact type and unites the advantages of Born scattering and short-wave asymptotic methods.

Keywords: wave propagation, method of the iteratived kernels.

 

Введение

Проблема распространения волн в различных средах, наряду с проблемами их генерации и приема, является основополагающей для акустики, радиофизики и оптики. К настоящему времени разработано большое количество различных приближенных методов теории распространения волн. Их можно разделить на два больших класса: методы, описывающие многолучевое взаимодействие излучения со средой (рассеяние волн), и методы, учитывающие многократное взаимодействие волны со средой (распространение волн).

К первому классу относятся теория однократного рассеяния, теория Тверского, теория многократного взаимодействия и уравнение Дайсона, уравнение переноса излучения и т.д [1, 2]. Эти методы хорошо описывают процесс взаимодействия волны с мелкомасштабными по сравнению с длиной волны неоднородностями среды, сопровождающийся образованием вторичного излучения в результате рассеяния. При этом изменение характеристик падающей волны не учитывается.

Второй класс методов образуют асимптотические методы, описывающие преимущественно изменение фазы падающей волны за счет прохождения через среду с крупномасштабными неоднородностями. При этом считается, что рассеяние происходит в основном в направлении распространения первичной волны, и им можно пренебречь. Наиболее важными представителями такого подхода являются метод геометрической оптики, метод плавных возмущений (приближение Рытова) и метод параболического уравнения [1, 2].

Задача же создания метода, одинаково эффективного для среды с разными масштабами неоднородностей, который описывал бы рассеянное поле и искажения падающей волны, к настоящему времени далека от решения. Поэтому при описании взаимодействия волны с неоднородной средой обычно используется только один доминирующий эффект – рассеяние, поглощение, рефракция, дифракция и т.д. – а все остальные не учитываются.

В статье предлагается приближенное решение уравнения Гельмгольца, основанное на применении метода итерированных ядер к эквивалентному интегральному уравнению. Поскольку точное вычисление итерированных ядер невозможно для произвольной пространственной зависимости диэлектрической проницаемости среды, применяется их приближенная оценка путем использования нескольких первых членов разложения Тейлора. Полученный ряд итерированных ядер удается просуммировать точно, что приводит к достаточно удобному для анализа результату.
 

1. Метод итерированных ядер

Будем рассматривать задачу распространения радиоволн в неоднородной безграничной среде в скалярном приближении. Как известно, в такой постановке задача определения полного поля сводится к решению неоднородного интегрального уравнения Фредгольма второго рода

(1)

Здесь поле  характеризует первичную волну,   возмущенное значение диэлектрической проницаемости среды относительно фонового значения ,  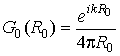– функция Грина однородной среды, , а объемный интеграл по безграничному пространству в правой части описывает рассеянное неоднородностями поле.

Можно показать [3], что, привлекая понятие резольвенты, решение интегрального уравнения можно представить в виде

,

(2)

где  – резольвента интегрального уравнения (1).

Основным методом решения интегрального уравнения (1) при произвольной пространственной зависимости контраста диэлектрической проницаемости  является метод итерированных ядер. В случае линейной среды резольвенту можно представить рядом Неймана

,

(3)

который сходится при достаточно малых значениях волнового числа . n+1-ое итерированное ядро  находится по следующему рекуррентному соотношению [3]

,

(4)

в котором  является ядром уравнения (1).

Основная трудность такого подхода заключается в громоздкости записи итерированных ядер, представляющих собой многомерные несобственные интегралы весьма сложного вида, суммировать которые не представляется возможным. Поэтому приходится либо ограничиваться малым количеством учитываемых ядер (борновское приближение, теория двукратного рассеяния [2] и т.д.), либо использовать упрощающие приближения.

Переходим к вычислению итерированных ядер. Первое ядро в нашем случае равняется

.

Второе итерированное ядро находится по формуле (4)

,

где , . В предположении достаточно плавного изменения  первый множитель в подынтегральном выражении можно разложить в ряд Тейлора в окрестности точки , ограничившись его линейными членами:

,

где введены обозначения 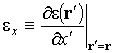 и т.д.

Отсутствие под интегралом произвольной функции позволяет вычислить интеграл точно [4]:

С использованием обозначений

, , ,

 

этот результат можно представить более компактно

Остальные итерированные ядра вычисляются аналогично. Приведем к примеру несколько первых итерированных ядер
 

 

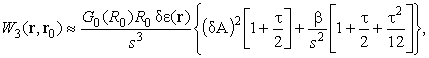
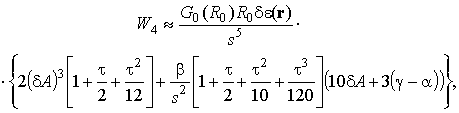
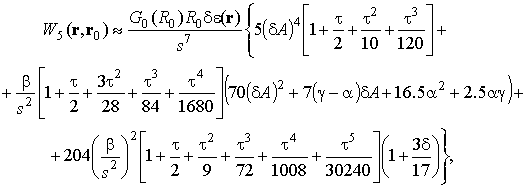
где введены обозначения

, , , .

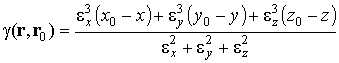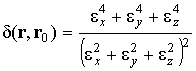       Уже первые вычисленные итерированные ядра демонстрируют  чрезвычайно сложную структуру точного решения задачи: в нем присутствуют все члены разложения по степеням первых производных диэлектрической проницаемости среды. И это только при рассмотрении линейных членов! Учет же дальнейших членов разложения Тейлора добавит в решение слагаемые, пропорциональные производным от  второго, третьего и всех последующих порядков в самых различных комбинациях. В то же время первые слагаемые каждого вычисленного ядра удовлетворяют общей закономерности

,

(5)

где коэффициенты  удовлетворяют рекуррентным соотношениям

.

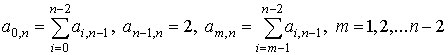После подстановки (5) в (3) резольвента запишется в виде

.

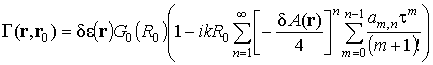Для вычисления этого двойного ряда используем метод, предложенный в [5] и базирующийся на отождествлении коэффициентов степенного ряда с ортогональным полиномом, вычисляемым по обобщенной формуле Родрига [6]. В результате приходим к следующему компактному представлению для резольвенты

,

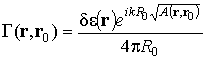где .

Таким образом, решение уравнения (1) примет вид

.

(6)

Выберем в качестве падающего поля поле точечного источника , . Тогда вычисление интеграла (6) дает функцию Грина уравнения Гельмгольца для неоднородной среды

,   .

(7)

Подчеркнем, что единственное сделанное в процессе преобразований приближение состоит в неточном учете зависимости  от координат. Предложенное решение объединяет в себе достоинства методов борновского рассеяния и геометрической оптики. Действительно, в случаях малых флуктуаций диэлектрической проницаемости, когда влиянием  можно пренебречь, наше решение совпадает с борновским. С другой стороны, показатель экспоненты, описывающий искажение волны, прошедшей неоднородную среду, можно отождествить с оптической длиной, составляющей основу метода геометрической оптики. Достоинством предложенного решения является его применимость для любого вида падающей волны и профиля неоднородности.
 

2. Оценка погрешности и сравнение с другими методами

Для определения места предложенного подхода среди других приближенных методов распространения волн в неоднородных средах оценим погрешности решения (6) и наиболее известных методов – борновского приближения и метода плавных возмущений.

Проблема оценки погрешности и установления границ применимости различных приближенных методов остается, пожалуй, наиболее туманной и спорной областью теории распространения волн [1, 2, 4]. Отдавая себе в этом отчет, в качестве критерия точности будем рассматривать невязку приближенного решения, подставленного в уравнение Гельмгольца. Для единообразия всюду будем рассматривать поле точечного источника – функцию Грина.

Начнем с борновского приближения

.

(8)

Подстановка в уравнение Гельмгольца приводит к выражению для невязки (при )

Вычисление интеграла в (8) с помощью методики, уже использованной при вычислении повторных ядер [4], дает

(9)

где  – оператор Лапласа.

Таким образом, условие применимости борновского приближения определяется, прежде всего, требованием малости контраста проницаемости неоднородностей относительно фоновой среды .

Функция Грина в приближении метода плавных возмущений имеет вид [2]

(10)

где

.

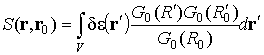Подстановка в уравнение Гельмгольца приводит к выражению для невязки
 

 

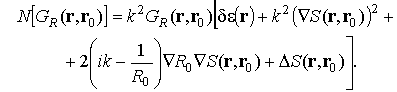
Вычислим производные первого и второго порядка от :
 

 

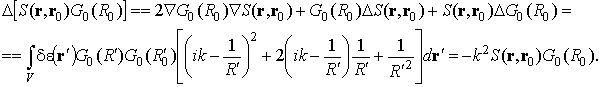
Следовательно,

,

и невязка метода плавных возмущений описывается соотношением

После приближенного вычисления интеграла для  

(11)

главный член невязки описывается выражением

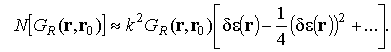
Таким образом, условием применимости метода плавных возмущений также является требование малости контраста неоднородностей среды . Этот результат является неожиданным, поскольку обычно считается, что метод предназначен для описания плавных сред, для которых мала не сама проницаемость, а ее градиент. Отметим, что для метода Рытова главный член погрешности не зависит от величины  в противоположность приближению Борна, что позволяет распространить результаты расчета на область протяженных трасс.

Исследуем теперь невязку уравнения Гельмгольца относительно рассматриваемого в этой статье решения (7)

.

Выражение невязки через  и ее производные выделяет следующую главную часть

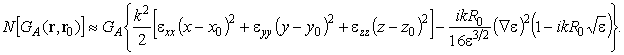
Таким образом, в отличие от известных методов, решение требует плавности изменения неоднородностей среды, т.е. малости не самой диэлектрической проницаемости, а ее первой и второй производных.

В заключение сравним выражения для функций Грина рассматриваемых приближений ,  и . Разложение экспоненциального множителя функции в (7)

приводит ее к выражению, идентичному формулам (10) – (11) для приближения Рытова

,

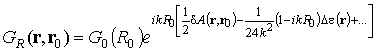а разложение экспоненциального множителя функции  в ряд Тейлора вплоть до линейных членов приводит ее к выражению приближения Борна (9).

Таким образом, сравнение различных приближенных методов между собой демонстрирует их удивительную схожесть в попытках уточнения фазовой зависимости функции Грина для неоднородной среды. Также можно заметить, как малейшие погрешности в определении функциональной зависимости фазы приводят к существенному понижению порядка точности метода.

 

Литература

1.     Рытов С.М., Кравцов Ю.А., Татарский В.И. Введение в статистическую радиофизику. Ч. 2. Случайные поля. – М.: Наука. Гл. ред. физ.-мат. лит., 1978. – 464 с.

2.     Исимару А. Распространение и рассеяние волн в случайно-неоднородных средах. Т. 1, 2. – М.: Мир, 1981. – 317 с.

3.     Трикоми Ф. Интегральные уравнения. – М.: ИЛ, 1960. – 300 с.

4.     Лосев Д.В., Бардашов Д.С. Метод итерированных ядер при распространении волн в неоднородных средах. – LAP Lambert Academic Publishing, 2014. – 60 с.

5.     Бардашов Д.С., Лосев Д.В. Метод резольвенты в теории распространения волн в неоднородных средах // Известия Вузов. Физика, 2006, № 9. – С. 19-22.

6.     Суетин П.К. Классические ортогональные многочлены. – М.: Наука. Гл. ред. физ.-мат. лит., 1979. – 416 с.