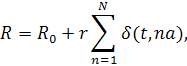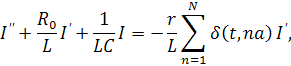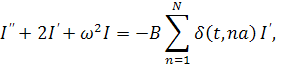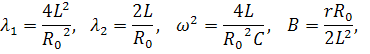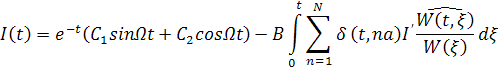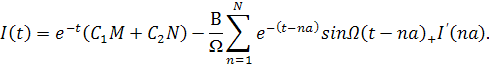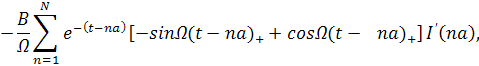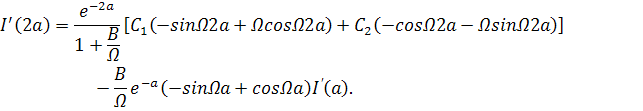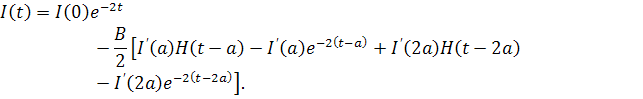Применение дифференциальных уравнений с переменными коэффициентами δ-функциями Дирака к исследованию последовательной RLC-цепи с дискретно – континуальными характеристиками

А. Б. Путилин¹, Р. Е. Либерзон¹, В. К. Курбаналиев^1,2
1Московский государственный университет машиностроения (МАМИ)

²ФГУП «ЦНИРТИ им. академика А.И. Берга»

Статья получена 15 декабря 2014 г.

Аннотация. Работа посвящена исследованию импульсного температурного воздействия на термистор в последовательном колебательном контуре. Температурное воздействие моделировалось δ-функциями Дирака. Показано, что в этом случае задача сводится к решению дифференциального уравнения с переменными коэффициентами δ-функциями Дирака. Получено точное решение в безразмерном критериальном виде. С использованием предельной теоремы построено асимптотическое представление функции тока в колебательном контуре при малых значениях времени. Показано, что при некоторых значениях времени, ток может стать больше наперед заданной величины, что может привести к сбою радиоэлектронной системы.
Ключевые слова: последовательный колебательный контур, термистор, δ-функция Дирака, асимптотическое представление, сбой аппаратуры, радиоэлектронная система. 

Abstract. The paper explores the effects of pulsed changes in temperature on a thermistor within a RLC circuit. The effects of temperature were represented in Dirac δ-functions. The study establishes that the solution lies in a differential equation with variable coefficients of Dirac δ-functions. An accurate dimensionless criteria solution has been obtained. An asymptotic representation of the current function in the resonance circuit at low time values has been constructed using the limit theorem. It has been proved that at certain time values the current can exceed a well-defined expected value, which may trigger the radio electronic system failure.

Key words: RLC circuit, thermistor, Dirac delta function, asymptotic representation, system failure, radio electronic system.  

Введение

В электрических цепях, так же как и в механических системах, могут возникать свободные колебания. Простейшей электрической системой, способной совершать свободные колебания, является последовательный RLC-контур (рис.1). Данная работа посвящена проблеме дополнительных пиковых значений последовательной RLC-цепи с термистором.

Эта проблема исключительно важна при разработке средств борьбы с кибертерроризмом, одной из главных опасностей ближайших десятилетий.

Рассмотрим последовательную RLC-цепь, содержащей термистор R, индуктивность L и емкость С, где могут возбуждаться электрические колебания.

 

Рис.1. Последовательный RLC – контур.

Если в качестве искомой величины выбрать силу тока , уравнение, описывающее свободные колебания в RLC-контуре, может быть приведены к следующему виду [1]: 

(1)

Здесь

Пусть сопротивление термистора имеет дискретно – континуальную характеристику, т.е.

(2)

здесь дельта-функция Дирака, na – носитель n-ой  – функции Дирака.
С учетом (2) уравнение (1) примет вид:

(3)

Обозначим:

,

Применяя теоремy подобия, перепишем уравнение (3) в безразмерном критериальном  виде:

(4)

где 

Введем обобщенную смещенную частоту собственных колебаний контура:

Общее решение  уравнения (4) можно записать в виде:

(5)

где  .

Здесь

определитель Вронского для фундаментальных функций уравнения (4)  

где

(6)

а  определитель, получаемый из определителя Вронского заменой последней строки на первую строку с аргументом t.

Тогда определить Вронского  W(ξ) будет иметь вид:

(7)

а определительзапишется так:

(8)

Здесь

, ,

(9)

Тогда из (5) с учетом (6) и (9) найдем:

(10)

Используя фильтрующее свойствоδ-функции:

получим

(11)

здесь

.

Теперь, вводя обозначение произвольной сингулярной функции вида

а также

общее решение перепишем в виде:

(12)

Чтобы найти константы , представляющие собой, скорость изменения тока в исследуемом устройстве в моменты времени, когда происходит тепловые воздействия, поступим следующим образом. В выражениибудем последовательно подставлять t=a, 2a, и т.д. В результате получим систему линейных алгебраических уравнений специального треугольного вида аналогично [2,3].  

Отметим, что n – ое уравнение этой системы является разностным аналогом интегрального уравнения Вольтерра 2-го рода. Таким образом после решения конечно - разностного уравнения Вольтерра 2-го рода можно получить точное решение для функции тока последовательной RLC – цепи с термистором.

Найдем (t): 

(13)

Рассмотрим частный случай двукратного воздействия импульсов тепла на термистор, из (13) найдем:

1)  t=a.

или

2) Аналогично для получим:

Асимптотическое поведение функции тока последовательной  RLC – цепи можно получить следующим образом.

Введя преобразование Лапласа по переменной t, с учетом теоремы дифференцирования оригинала дифференциальное уравнение (4) можно переписать в виде алгебраического уравнения относительно изображения:

L[

(14)

Такой подход удобен, если из соображений целесообразности нужно знать асимптотическое поведение искомой функции при больших или малых значениях времени. Согласно предельной теореме операционного исчисления при малых значениях времени t асимптотическое представление изображения при больших p будет иметь вид:

L[

(15)

Переходя здесь почленно к функциям оригиналам, с использованием теоремы запаздывания, получим асимптотическое представление тока I при малых значениях времениt после импульсного теплового воздействия на термистор.

(16)

Из (16) очевидно, что всегда найдутся такие значения времени t, при которых сумма положительных слагаемых в случае многократного воздействия на термистор может стать больше наперед заданной величины, что приведет к сбою радиоэлектронных систем.

Литература

1. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. Москва. Издательство «Высшая школа», 1996 г.
2. Р.Е.Либерзон, А.В.Миронова. Новый метод решения сингулярных задач теории    теплопроводности дискретно-континуальных сред. // «Новые технологии», №1, 2002.
3. Р.Е.Либерзон, А.В.Миронова. Об одной конечноразностной системе уравнений специального вида. // «Новые технологии», №3, 2002.

4. Дельта-функция. «Математика»  [электронный ресурс]. URL: http://mathworld.wolfram.com/DeltaFunction.html