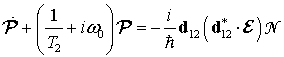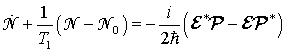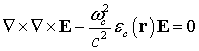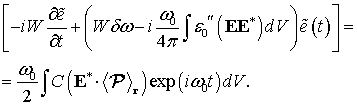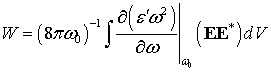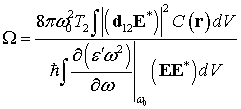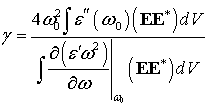Полуклассическая теория спазера на основе графена

УДК 621.373.826

Полуклассическая теория спазера на основе графена

И. А. Нечепуренко^1,2, А. В. Дорофеенко^1,2,3, Ю. Е. Лозовик^1,2,3,4,5

¹Всероссийский научно-исследовательский институт автоматики им. Н.Л. Духова

²Московский физико-технический институт (Государственный университет)
³Институт теоретической и прикладной электродинамики РАН

⁴Институт спектроскопии РАН

⁵Национальный исследовательский ядерный университет «МИФИ

Статья поступила в редакцию 7 декабря 2015 г.

Аннотация. В данной работе рассмотрен поверхностный плазмон-поляритонный лазер (спазер), который генерирует поверхностные плазмоны в графеновой чешуйке. Произведен пересмотр основных лазерных уравнений для описания спазера с учетом дисперсии материальных параметров. Выполнен последовательный вывод уравнений динамики спазера, начиная с уравнений Максвелла-Блоха. Получены уравнения динамики спазера в одномодовом приближении и скоростные уравнения. Найдены выражения для параметров уравнений через физические параметры системы. Приведены характерные численные значения параметров скоростных уравнений, описывающих динамику спазера на основе графена.

Ключевые слова: плазмонный генератор, плазмоника графена, спазер на основе графена, уравнения Максвелла-Блоха, скоростные уравнения.

Abstract: In the present paper graphene nanoflake generator (spaser) is considered. Consistent derivation of main equations for the description of graphene spaser dynamics with the account of the material dispersion is provided. Single-mode equations and rate equations are derived. Explicit expressions for the parameters in the equations are obtained. Numerical values of these parameters, which describe graphene spaser dynamics, are given.

Keywords: plasmonic generator, graphene plasmonics, graphene spaser, Maxwell-Bloch equations, rate equations.

Введение

Недавнее развитие плазмоники [1-12] сделало возможным создание плазмонных устройств, аналогичных устройствам классической оптики. Разнообразные плазмонные линзы, зеркала и резонаторы исследованы теоретически и экспериментально [13-18]. Основные преимущества плазмонных устройств по сравнению с оптическими – это способность к субволновой фокусировке электромагнитной энергии и создание высокой интенсивности поля, что в свою очередь приводит к возможности сильного взаимодействия поля с веществом. Поверхностные плазмоны играют важную роль в спектроскопии, усиленной поверхностью. Высокая локализация поля плазмонов увеличивает чувствительность спектроскопии поглощения к присутствию молекул на поверхности [19-23]. Указанный эффект, в частности, вносит свой вклад в гигантское комбинационное рассеяние (SERS) [24-27], что сделало возможным обнаружение единичных молекул [28].

Приложения плазмоники ограничены омическими потерями в металле. Поэтому предложено использовать активные среды для компенсации потерь [29, 30] и усиления [31] поверхностных плазмонов (ПП), распространяющихся вдоль активных наноструктур. Усиление может привести к генерации поверхностных плазмонов [32-37]. Кроме того, было установлено, что поверхностные плазмоны, локализованные на наночастицах, также могут когерентно генерироваться безызлучательным возбуждением [38-43]. Об экспериментальной реализации такой системы – спазера – сообщалось несколькими группами [44-48]. В целом, различие между генератором ПП (в английской литературе называемым «SPP laser») и спазером является нечетким, так что часто они отождествляются [49]. С другой стороны, эти два устройства можно рассматривать как противоположные предельные случаи, соответственно, большого резонатора для ПП и малой (наноскопической) системы. Кроме многочисленных перспективных приложений, плазмонные генераторы интересны сами по себе как передовые устройства квантовой плазмоники [50, 51].

Одним из наиболее перспективных плазмонных материалов является графен [52-57]. Графен представляет собой очень тонкий двумерный материал [58, 59], имеющий чрезвычайно высокую подвижность носителей [60]. Этот материал поддерживает распространение плазмонов, причем возможно управление свойствами материала путем варьирования уровня Ферми, например, с помощью дополнительного электрода [61]. Область применимости графена лежит от оптического до терагерцового частотного диапазона. Эти области чрезвычайно важны для приложений, поскольку именно там находятся колебательные переходы молекул. Использование графена открывает возможности для создания высокочувствительных компактных терагерцовых устройств. В ближней ИК-области локализация графеновых плазмонов максимальна, а потери при этом существенно меньше, чем в металл-содержащих плазмонных системах [62]. Несмотря на относительно низкое поглощение в графене, потери все же серьезно ограничивают длину свободного пробега плазмонов, что является основным препятствием для приложений графеновой плазмоники. В результате начала развиваться активная плазмоника графена [63]. В частности, предложены генераторы плазмонов на графене на основе различных усиливающих сред (квантовых точек, квантовых ям, углеродных нанотрубок) [64-66].

В настоящей работе получены уравнения динамики спазера в одномодовом приближении с учетом материальной дисперсии. Для случая спазера на основе графеновой наночешуйки приведены численные оценки параметров в скоростных уравнениях.

Уравнения динамики графенового спазера в одномодовом приближении

Рассмотрим спазер, состоящий из активной среды (например, квантовых точек) и резонатора для поверхностных плазмонов. Этот резонатор может быть реализован как графеновая наночешуйка. Усиливающая среда имеет больший коэффициент связи с плазмонной модой, чем с вакуумными электромагнитными модами. Поэтому только безызлучательная генерация плазмонов будет принята во внимание.

Усиливающая среда моделируется как двухуровневая система. В этом случае уравнения для элементов матрицы плотности преобразуются в уравнения для дипольного момента частицы усиливающей среды и инверсии населенностей . Добавление уравнений Максвелла для электрического поля дает уравнения Максвелла-Блоха [67-69]:

, (1)

, (2)

. (3)

Здесь и относятся к некоторой конкретной частице усиливающей среды. Эти частицы распределены с пространственной плотностью . Угловые скобки с нижним индексом , , означают усреднение по частицам, находящимся в физически бесконечно малом объеме в окрестности точки .

Предположим, что плазмонная генерация происходит в одномодовом режиме. Будем считать, что распределение поля в спазерном резонаторе совпадает с распределением поля моды пассивного резонатора, рассчитанной в отсутствие активной среды. Кроме того, используем приближение медленных амплитуд, рассматривая частоту перехода усиливающей среды как несущую частоту. В таких предположениях поле записывается в виде:

, (4)

где – медленная амплитуда поля. Распределение электрического поля в пространстве определяется следующим уравнением:

, (5)

где – распределение диэлектрической проницаемости (с учетом проводимости графена) на собственной частоте резонатора .

Подставим (4) в (1) и скалярно умножим обе части полученного уравнения на . Далее вычтем из полученного уравнения результат комплексного сопряжения уравнения (5), скалярно умноженного на величину . Последовательность указанных операций может быть записана как . Результат имеет вид

(6)

Производная по времени, стоящая в квадратных скобках в уравнении (6), в приближении медленных амплитуд принимает следующий вид с учетом дисперсии диэлектрической проницаемости [70]:

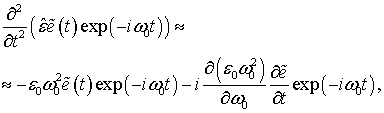(7)

где – пространственное распределение диэлектрической проницаемости на частоте перехода . Выражение в квадратных скобках в уравнении (6) можно преобразовать следующим образом:

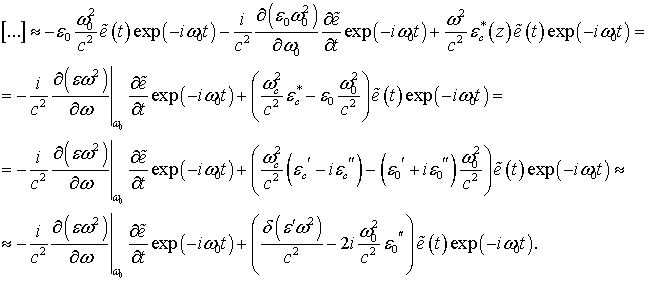
Здесь 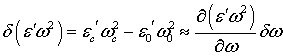и .

Таким образом, уравнение (6) приводится к виду:

(8)

Далее, проинтегрируем уравнение (8) по объему. Выражение в фигурных скобках преобразуется следующим образом:

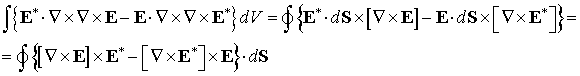
Последнее выражение описывает потери на излучение, которым мы пренебрежем по сравнению с поглощением в графене. Таким образом, уравнение (8) принимает вид:

(9)

Здесь введено обозначение

. (10)

Кроме того, в уравнении (9) исключена из рассмотрения мнимая часть множителя , а временная производная поляризации раскрыта как .

Переобозначим медленную амплитуду поля , чтобы она не зависела от нормировки моды резонатора , так что уравнение (4) приводится к виду

. (11)

Вводя время релаксации в соответствии с соотношением

(12)

и медленную амплитуду поляризации усиливающей среды

, (13)

запишем уравнение на поле:

. (14)

Чтобы получить уравнение на , нужно усреднить обе части уравнения (2) по физически бесконечно малому объему (операция ), затем скалярно умножить полученное уравнение на и проинтегрировать обе части по всему объему. Результат этих операций имеет вид:

. (15)

Интеграл в правой части описывает взаимодействие поля с неоднородным пространственным распределением инверсии населенностей . Предположим, что эффект неоднородности усиливающей среды не являются существенными в рассматриваемой системе. Тогда можно заменить средним значением инверсии населенностей в частице среды, равным отношению общей инверсии квантовых точек, , к числу усиливающих частиц :

. (16)

Тогда интеграл в правой части уравнения (15) преобразуется к виду:

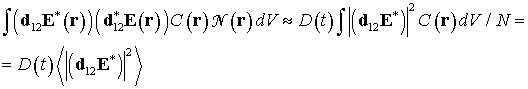
В этом приближении, вводя параметр взаимодействия в виде

, (17)

получим уравнение на поляризацию усиливающей среды:

. (18)

Чтобы получить уравнение для инверсии, усредним обе части уравнения (3) по физически бесконечно малому объему (операция ). На втором этапе, выразим поле в соответствии с уравнением , а затем умножим обе части полученного уравнения на концентрацию и проинтегрируем по пространству. Далее, учитывая уравнение , имеем

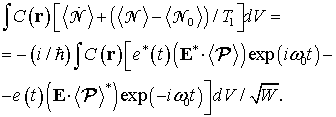
В соответствии с введенным определением, запишем и, аналогично, . Последнее замечание, вместе с определением амплитуды поляризации (13) приводит к уравнению на инверсию населенностей:

. (19)

Подводя итог, лазерная динамика в одномодовом приближении описывается уравнениями (14), (18), (19) :

, (20)

, (21)

(22)

с параметрами, определенными уравнениями (12), (17).

Отметим, что инверсия населенностей одиночной частицы не может превышать единицу по абсолютной величине. Таким образом, общая инверсия населенностей меняется в пределах .

Скоростные уравнения

Заметим, что типичное время поперечной релаксации нанокристаллических квантовых точек с на несколько порядков меньше времени продольной релаксации с. Кроме того, также много меньше времени жизни моды резонатора с (см. следующий раздел). Это значит, что рассматриваемый генератор относится к классу B [69], и в качестве поляризации усиливающей среды в уравнения (20), (22) можно подставить ее квазистационарное значение

, (23)

которое находится из уравнения (21), считая и предполагая . В этом случае уравнения (20) и (22) преобразуются к виду

, (24)

. (25)

Наконец, введем переменную для числа плазмонов в резонаторе . Это определение согласуется с соотношением между энергией электромагнитного поля и количеством плазмонов: . В результате мы можем записать уравнения на и :

(26)

(27)

где и .

Численные оценки параметров ,

В соответствии с вышеприведенным выводом, параметры в уравнениях (26), (27) определяются выражениями

, (28)

. (29)

Рассмотрим достаточно общий случай спазера с резонатором в виде чешуйки графена, находящейся на диэлектрической подложке. Тогда диэлектрическая проницаемость как функция координаты равна диэлектрической проницаемости подложки при , единице при и диэлектрической проницаемости графена при . Графен – очень тонкий материал, обладающий чрезвычайно высокой подвижностью. Обычно его оптические свойства характеризуются комплексной поверхностной проводимостью , которая связана с объемной проводимостью соотношением . Тогда вклад графена в общую диэлектрическую проницаемость имеет вид . В таком случае имеем , что сводит числитель в (29) к значению , где – площадь графена, –тангенциальная компонента электрического поля, и индекс “g” означает, что напряженность поля рассчитывается на слое графена. Таким же образом, считая усиливающий слой очень тонким, можно оценить числитель в (28) как . В предположении, что дипольный момент усиливающей среды параллелен слою графена, последнее выражение переходит в . Интеграл в знаменателях выражений (28), (29) вычисляется следующим образом:

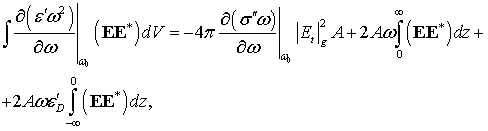
где – диэлектрическая проницаемость подложки. Пусть и – мнимые части нормальных составляющих волновых векторов в вакууме и диэлектрике, так что и , где – волновое число поверхностного плазмона и . Зависимость электрического поля от z имеет вид в подложке () и (). Это приводит к следующему выражению для интеграла в знаменателях выражений (28), (29):

.
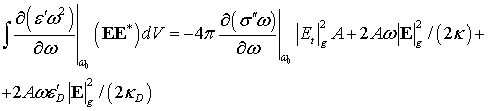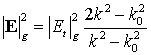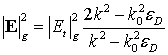Наконец, примем во внимание связь между тангенциальной и нормальной составляющими электрического поля: в вакууме и в подложке. Учитывая также соотношение , находим в вакууме и в подложке. Для плазмона в графене имеем , что означает . В том же приближении , что приводит к соотношению

.
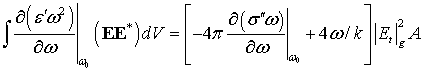Тогда выражения для констант, фигурирующих в скоростных уравнениях, принимают вид:

, (30)

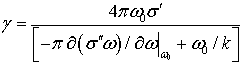, (31)

где обозначает поверхностную плотность частиц усиливающей среды (например, квантовых точек).

Для частоты , соответствующей длине волны 6 мкм, проводимость графена и , а волновое число плазмона на графене . Мы рассматриваем следующие параметры квантовых точек: , (1 Д = единиц СГС) и концентрацию квантовых точек, соответствующую площади 20 нм x 20 нм, приходящейся на каждую квантовую точку. Это приводит к значениям и .

Выводы

В заключение, в данной работе выведены уравнения, описывающие динамику спазера на основе графена. Получены выражения для параметров, которые необходимы для описания динамики спазера. Найдены характерные численные значения этих параметров.

Работа выполнена при финансовой поддержке Фонда перспективных исследований (контракт номер 7/004/2013-2018 от 23.12.2013) и Российского фонда фундаментальных исследований.

Литература

1. S. A. Maier. Plasmonics: Fundamentals and Applications. New York: Springer Science + Business Media, 2007.

2. G. Shvets, I. Tsukerman. Plasmonics and Plasmonic Metamaterials: Analysis and Applications. Singapore: World Scientific, 2012.

3. S. Enoch, N. Bonod. Plasmonics: From Basics to Advanced Topics. Berlin: Springer Series in Optical Sciences, 2012.

4. S. Zouhdi, A. H. Sihvola, A. P. Vinogradov. Metamaterials and Plasmonics: Fundamentals, Modelling, Applications. New York: Springer Science + Business Media B.V., 2009.

5. S. I. Bozhevolnyi. Plasmonic nanoguides and circuits. Singapore: Pan Stanford Publishing Pte Ltd, 2009.

6. V. M. Shalaev, S. Kawata. Nanophotonics with Surface Plasmons Amsterdam: Elsevier B.V., 2007.

7. A. V. Zayats, S. Maier. Active Plasmonics and Tuneable Plasmonic Metamaterials. Hoboken: John Wiley and Sons, 2013.

8. A. K. Sarychev, V. M. Shalaev. Electrodynamics of Metamaterials. Singapore: World Scientific Publishing Co. Pte. Ltd., 2007.

9. P. R. West, S. Ishii, G. V. Naik, N. K. Emani, V. M. Shalaev, A. Boltasseva. Searching for better plasmonic materials // Laser & Photonics Reviews. 2010. V. 4. N 6. P. 795-808.

10. Y. E. Lozovik, A. V. Klyuchnik. The dielectric function and collective oscillations inhomogeneous systems // Dielectric Susceptibility / Keldysh L. V. и др. North Holland: Amsterdam, 1987. C. 299.

11. P. N. Melentiev, A. E. Afanasiev, A. A. Kuzin, A. S. Baturin, V. I. Balykin. Giant optical nonlinearity of a single plasmonic nanostructure // Optics express. 2013. V. 21. N 12. P. 13896-13905.