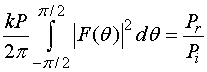УДК 621.396.67

СВЕРХШИРОКОПОЛОСНАЯ ОБЛУЧАЮЩАЯ СИСТЕМА НА ОСНОВЕ ЛИНЕЙНОЙ РЕШЕТКИ ИЗ АНТЕНН ВИВАЛЬДИ

ДЛЯ МНОГОЛУЧЕВЫХ ГИБРИДНЫХ АНТЕНН

 

С. Е. Банков ¹, М. Д. Дупленкова ², В. А. Калошин ¹

¹ ИРЭ им. В.А. Котельникова РАН

² Национальный исследовательский университет Московский энергетический институт

 

Статья поступила в редакцию 10 декабря 2015 г.

 

Аннотация. Исследованы характеристики бесконечной одномерной решетки из антенн Вивальди в режиме возбуждения одного элемента решетки. С использованием метода конечных элементов найдены зависимости элементов матрицы рассеяния на стыке периода решетки - канала Флоке в квазипериодическом режиме для разных значений фазового сдвига между полями в соседних каналах. В приближении теории бесконечных фазированных решеток рассчитана амплитудная и фазовая диаграммы направленности элемента решетки. В широком диапазоне частот исследованы форма амплитудной диаграммы направленности и положение ее фазового центра. Показана возможность создания кластерного облучателя при одновременном возбуждении нескольких элементов решетки для обеспечения заданного уровня пересечения лучей многолучевой антенны в сверхширокой полосе частот при сохранении высокого значения КИПа.

Ключевые слова: антенная решетка, антенна Вивальди, сверхширокая полоса частот, канал Флоке.

Abstract. Characteristics of an infinite linear array of Vivaldi antennas in regime of excitation of the array element are investigated. A problem of calculation of Floquet channel scattering matrix for different values of phase shift between fields in neighboring array elements is solved with using of finite elements method. Phase and amplitude radiation pattern of the array element are calculated in frame of theory of infinite antenna arrays. Shape of radiation pattern and position of its phase center are analyzed in the wide frequency range. A possibility of a cluster type radiator design using a set of the array active elements to obtain a given level of beams intersection and a high level of efficiency of a multi-beam antenna is shown.

Keywords: antenna array, Vivaldi antenna, wide frequency range, Floquet channel.

 

Введение

         Проблема создания сверхширокополосных (СШП) многолучевых антенн давно привлекает внимание разработчиков радиоэлектронной аппаратуры и исследователей [1]. Один из перспективных путей решения этой задачи – использование гибридных антенн, содержащих фокусирующую систему и облучающую систему в виде решетки [2]. Функцию фокусирующей системы может выполнять зеркало или линза, в частности, линза Люнебурга, которая может обеспечить очень широкий сектор обзора [2,3].

         Отметим, что зеркало, диэлектрическая или шнурковая линза на основе ТЕМ линий не имеют серьезных ограничений на полосу рабочих частот. Поэтому основным элементом, ограничивающим частотный диапазон многолучевой гибридной антенны (МГА), является облучающая система. При этом можно рассматривать различные режимы работы антенны, два из которых предполагают обеспечение заданного уровня пересечения лучей. В одном из них (с постоянным числом облучателей) необходимо обеспечить постоянство ширины луча антенны в рабочей полосе частот. Усиление антенны и КИП при этом, разумеется, будут падать с увеличением частоты. В другом режиме КИП антенны поддерживается на высоком уровне за счет стабилизации ширины диаграммы направленности (ДН) облучателя и положения его фазового центра. При этом для обеспечения заданного уровня пересечения лучей необходимо обеспечить изменение числа облучателей при изменении частоты. В данной работе исследуется второй режим с использованием кластерного СШП облучателя в виде одномерной решетки из антенн Вивальди. Способы регулирования числа облучателей в кластере в зависимости от частоты в работе не рассматриваются.

Известно весьма большое число работ, посвященных исследованию СШП решеток (см., например, [4-7]). В большинстве этих работ рассматриваются решетки из антенн Вивальди, а анализ проводится в режиме квазипериодического возбуждения. Это интересно с точки зрения  их применения в качестве фазированных антенных решеток (ФАР). Для анализа возможности использования решетки в качестве облучателя МГА интересен режим возбуждения одного элемента, который легко обобщается на случай возбуждения нескольких элементов, соответствующий кластерному облучателю. Исследованию решетки антенн Вивальди в данном режиме посвящена наша работа.

Переход от квазипериодического режима, удобного для численных расчетов, к возбуждению одного канала решетки можно осуществить по известным соотношениям теории бесконечных ФАР [8]. Эти соотношения  позволяют по матрице рассеяния канала Флоке найти все интересующие нас параметры элементарного излучателя в составе решетки.    Расчет элементов матрицы рассеяния канала Флоке будем проводить методом конечных элементов.

 

 1. Модель для численного исследования

         В качестве модели облучателя используем двумерную бесконечную решетку антенн Вивальди, расположенную между двух металлическихплоскостей, расположенных горизонтально и образующих планарный волновод (рис. 1). Анализ электродинамических характеристик решетки в квазипериодическом режиме можно свести к анализу параметров одного периода (канала Флоке). Он представляет собой волноводную структуру, которая с одной стороны имеет вход (порт) в виде выхода антенны Вивальди, а с другой в виде виртуального порта Флоке [9]. Порт Флоке является моделью плоской волны свободного пространства.

         На металлических стенках установлены граничные условия равенства нулю тангенциальных компонент электрического поля :

         .                                                                                          (1)

 

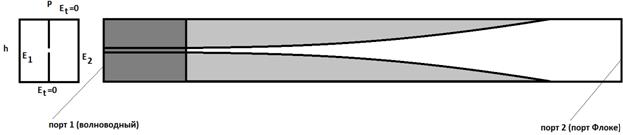
Рис. 1. Модель для численного исследования

 

         На вертикальных стенках канала Флоке установлены граничные условия периодичности:

         ,                                                                          (2)

где  - волновое число свободного пространства,  - период решетки,  - угол, под которым излучает решетка в плоскости XOZ, угол отсчитывается от оси 0z. Смысл полей  - поясняется на рис. 1.

         На торцах канала Флоке установлены порты 1 и 2. Порт 1 это волноводный порт, для установки которого на левом конце канала введен металлический волновод с размерами , в котором размещен отрезок щелевой линии. На правом конце канала установлен порт Флоке.

         Структура на рис. 1 отличается от используемых на практике антенн Вивальди, которые содержат переход от щелевой линии на одну из линий передачи, как правило, на микрополосковую линию. Разработка такого перехода представляет собой самостоятельную задачу, которая требует отдельного анализа. Ее решение влияет на полосу рабочих частот антенны, однако никак не сказывается на форме ДН, исследование которой является главной целью данной работы.

         Анализ возможности применения сосредоточенного порта, включенного между проводниками щелевой линии, показал, что такой порт для щелевой линии передачи имеет исключительно активное внутреннее сопротивление лишь на сравнительно низких частотах. При повышении частоты его импеданс приобретает существенную мнимую часть, что приводит к рассогласованию с линией передачи. Поэтому от использования таких способов моделирования входа антенны Вивальди пришлось отказаться.

         Пустой канал Флоке в общем случае является двухволновой структурой, что соответствует распространению в свободном пространстве двух волн с ортогональными поляризациями. На высоких частотах, когда выполняется неравенство

                                                                                                 (3)

где  - длина волны в свободном пространстве, в канале Флоке при определенных углах излучения могут распространяться высшие типы волн.

Таким образом, канал Флоке является многоволновой структурой. Поэтому порт Флоке также является многомодовым портом, а весь канал Флоке описывается в общем случае многомодовой матрицей рассеяния.  Поскольку сканирование происходит только в плоскости XOZ, то есть в плоскости вектора магнитного поля , то одна из волн канала Флоке, а именно волна поляризованная в указанной плоскости не возбуждается и не влияет на характеристики антенны. Поэтому на низких частотах (см. формулу (3)) пустой канал Флоке можно условно считать одномодовым. В этом случае вся структура в целом является СВЧ четырехполюсником. Наибольший интерес для наших целей представляет коэффициент передачи . Нижний индекс соответствует стандартной индексации матрицы рассеяния, а верхний индекс показывает, что данный элемент матрицы рассеяния определен для основной волны канала Флоке, которой мы присвоили нулевой номер.

         Теория бесконечных антенных решеток [8] позволяет связать в одноволновом режиме коэффициент передачи  с ДН одиночного элемента решетки :

         .                                                         (4)

         В многоволновом режиме связь имеет более сложный вид:

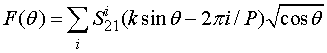         .                                     (5)

 

         Суммирование в соотношении (5) ведется только по слагаемым, удовлетворяющим условию:

         ,                                                                        (6)

         .

 

         ДН (5) нормирована следующим образом:

         ,                                                             (7)

где  соответственно мощность излучения и мощность падающей на вход антенны Вивальди волны.

 

2. Численные результаты расчета коэффициента передачи канала Флоке

         Рассмотрим некоторые результаты исследования частотных зависимостей элементов матрицы рассеяния канала Флоке при разных значениях угла излучения .

         На рис. 2 показана такая зависимость, полученная при , , длина антенны Вивальди с переменной шириной щели . Здесь и далее все размеры приводим в миллиметрах. Нетрудно увидеть, что коэффициент передачи при излучении по нормали к решетке () практически во всем частотном диапазоне от 0.5 до 16 ГГц близок к единице. Это означает, что практически вся мощность, поступившая на входы решетки излучается в плоский волновод. Также обращает на себя внимание, что даже на частоте 0.5 ГГц коэффициент передачи больше 0.9, то есть коэффициент отражения от решетки меньше 0.3.

         При изменении угла излучения картина на высоких частотах резко меняется уже при . Эти изменения видны на рис. 3, на котором показана частотная зависимость коэффициента передачи при указанном выше угле и геометрических параметрах структуры.

 

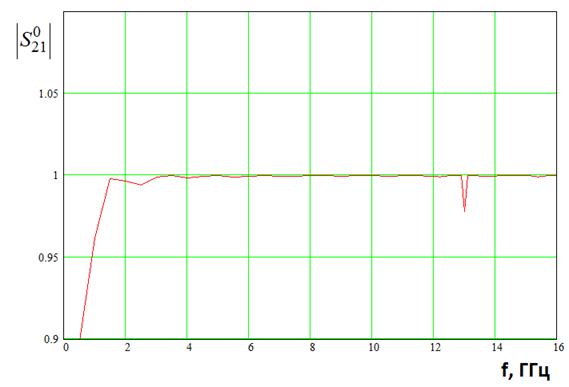
Рис. 2. Частотная зависимость модуля коэффициента передачи при

 

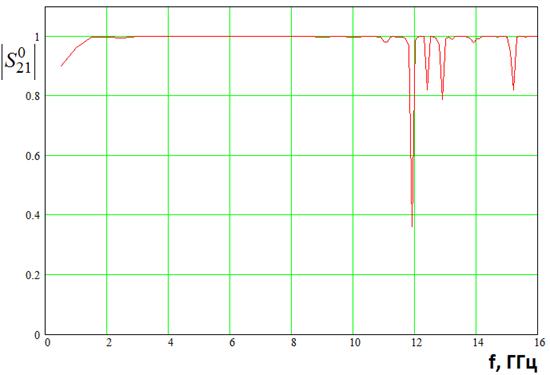
Рис. 3. Частотная зависимость модуля коэффициента передачи при

          

         Видно, что уже на частотах выше 12 ГГц возникают резонансные явления, сопровождающиеся резкими провалами коэффициента передачи. В этих зонах энергия либо отражается от решетки, либо излучается в других направлениях под углами отличными от угла . В этих направлениях энергия может уноситься волнами высших порядков, которые появляются при  ГГц.

         То, что границей зоны существования резонансов является частота 10 ГГц, хорошо видно из рис. 4, на котором представлена частотная зависимость коэффициента передачи при .

 

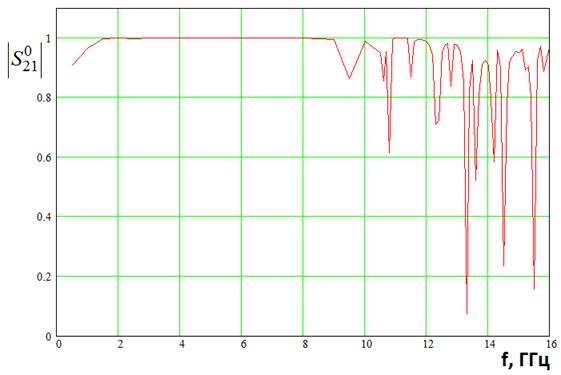
Рис. 4. Частотная зависимость модуля коэффициента передачи при

 

         Видно, что начиная, с частот немного ниже 10 ГГц кривая носит изрезанный характер. Отсюда можно сделать вывод о том, что диапазон частот, задаваемый неравенством (3) при использовании в качестве облучателя одного элемента решетки является непригодным для работы, поскольку его ДН имеет искаженную форму.

         В качестве примера приведем ее на частоте 12 ГГц (рис. 5).

 

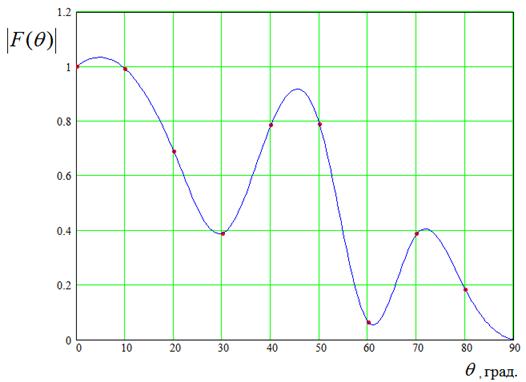
Рис. 5. ДН на частоте 12 ГГц

 

         Точками показаны результаты численных расчетов. Сплошная кривая получена их аппроксимацией кубическими сплайнами.

 

3. Характеристики излучения элемента решетки

         В этом разделе мы рассмотрим характеристики излучения одиночного элемента решетки антенн Вивальди в рабочем диапазоне частот. Анализ будем проводить на примере решетки с параметрами приведенными выше.

         Важным параметром облучателя является коэффициент передачи по мощности :

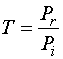         ,                                                                                          (8)

рассчитываемый по формуле (7). Он показывает энергетическую эффективность элемента решетки как антенны. На рис. 6 представлена частотная зависимость данного параметра для исследуемой решетки антенн Вивальди.  

 

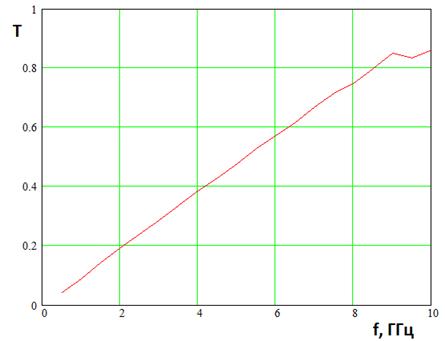
Рис. 6. Частотная зависимость коэффициента передачи по мощности

 

         Видно, что эффективность практически линейно растет вплоть до граничной частоты равной 10 ГГц. Далее зависимость параметра  от частоты имеет осциллирующий характер. Отметим, что линейная частотная зависимость определяется множителем  в соотношении (7).

         Может возникнуть вопрос: почему на низких частотах эффективность настолько мала, хотя решетка в квазипериодическом режиме при этом достаточно хорошо согласована. Дело в том, что возбуждение одного элемента решетки согласно [8] эквивалентно возбуждению ее в квазипериодическом режиме спектром волн, который равномерно распределен в пределах:

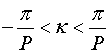         ,                                                                                 (9)

 

где  - спектральный параметр, который в зоне видимых углов связан с углом излучения:

         .                                                                                    (10)

         Однако, из неравенства (9) видно, что спектр возбуждающих решетку волн захватывает также зону мнимых углов, соответствующих комплексным значениям . В этой зоне решетка не излучает. Вся энергия падающих волн отражается назад. Причем с уменьшением частоты отношение ширины зоны мнимых углов к полной ширине спектра уменьшается и поэтому энергия отраженных волн увеличивается, что и приводит к падению энергетической эффективности.

 

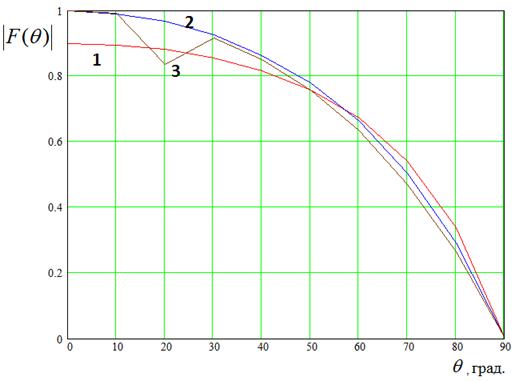
Рис. 7. ДН одиночного элемента решетки на частотах 0.5, 1.5, 9.5 ГГц

 

         На рис. 7 показана амплитудная ДН элемента решетки. Кривые 1 - 3 получены для  ГГц. В диапазоне от 1.5 до 9.5 ДН остается практически неизменной и весьма близка к функции , которая описывает ДН элемента идеально согласованной решетки [8].

         Фазовая ДН имеет большое значение для облучателя оптической системы. На рис. 8 показаны такие ДН антенны Вивальди в составе решетки. Кривые 1 - 3 получены на частотах 0.5, 5.5, 9.5 ГГц.

 

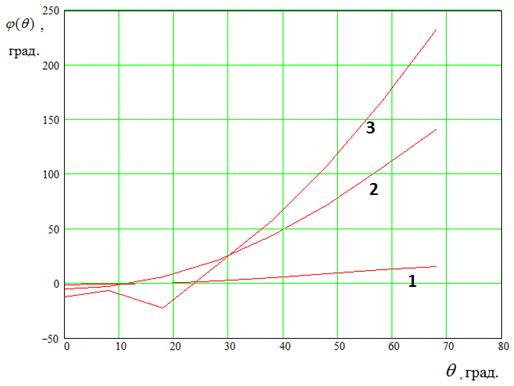
Рис. 8. Фазовая ДН элемента решетки

 

         На кривой 3 имеется излом, связанный с возбуждением высшего типа волны. В остальном диапазоне частот кривые имею гладкий характер, соответствующий квадратичной функции.

         Найдем фазовый центр излучателя, аппроксимируя фазовую ДН следующим образом:

         .                                                                              (11)

         Параметр  выбирается из условия наилучшего приближения аппроксимации к исходной функции. Он определяет смещение фазового центра вдоль оси 0z относительно начала координат. При численных расчетах начало координат совпадало с выходной плоскостью решетки. В этом случае положительное значение  соответствует смещению фазового центр внутрь антенны Вивальди.

 

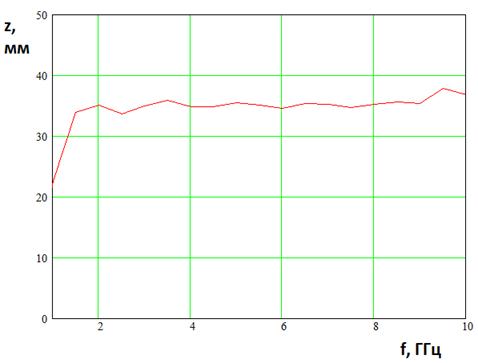
Рис. 9. Положение фазового центра в диапазоне частот

 

         На рис. 9 показана частотная зависимость фазового центра. Видно, что в широком диапазоне частот его положение остается практически неизменным. Колебания не превышают одного миллиметра. На очень низких частотах наблюдается резкое смещение фазового центра. Однако этот эффект не имеет существенного значения по двум причинам, так как длина волны на этих частотах велика. Например, на частоте 1 ГГц центр сдвинулся относительно стационарного значения на 10 мм, то есть всего лишь на 1/30 длины волны. Такое изменение положения фазового центра излучателя не играет роли при использовании его в качестве облучателя.

 

4. Характеристики излучения подрешетки

         Рассмотрим далее характеристики излучения подрешетки, которая формируется  элементами решетки, которые возбуждаются одинаковыми волнами единичной амплитуды. Для определения ДН подрешетки  мы можем воспользоваться элементарной теорией решеток, поскольку все эффекты взаимодействия учтены в ходе строгого расчета ДН элемента решетки:

         ,                                                           (12)

где  - ДН элемента решетки.

         Рассмотрим поведение коэффициента передачи подрешетки  в свободное пространство. Данный параметр рассчитывается по методике представленной выше для одиночного излучателя.

 

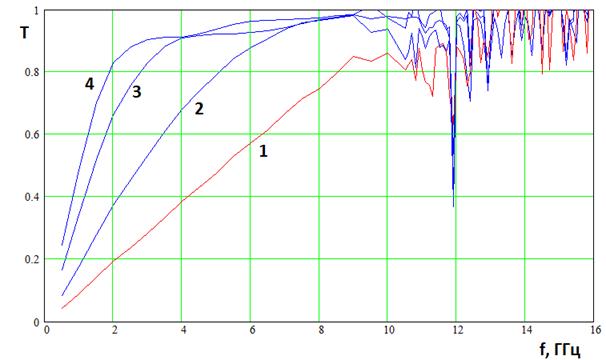
Рис. 10. Частотная зависимость коэффициента передачи подрешетки в свободное пространство

         На рис. 10 показана указанная зависимость. Кривые 1 - 4 получены, соответствен, для =1,2,4,6. Видно, что с увеличением числа элементов в кластере коэффициент передачи на низких частотах существенно возрастает, расширяя рабочий диапазон в область низких частот. Также можно отметить некоторое его расширение и в области высоких частот. Смещение нижней границы рабочего диапазона объяснить достаточно легко, поскольку в соответствии с теории решеток возбуждение нескольких ее элементов можно рассматривать как возбуждение одного элемента решетки, у которой период в  раз больше периода исходной структуры. В этом случае ширина спектра пространственных гармоник, возбуждающих решетку уменьшается в  раз и, следовательно, относительная ширина зоны видимых углов увеличивается, что приводит к уменьшению коэффициента отражения от решетки. Увеличение верхней границы рабочего диапазона связано с сужением ДН подрешетки относительно ДН одного элемента. Поскольку резонансные явления преимущественно наблюдаются в квазипериодическом режиме в области углов  далеких от нулевого, то они искажают ДН подрешетки значительно слабее ДН элемента.

         Если оценить полосу согласования кластера по уровню = 0.9, можно заметить, что она растет почти линейно с ростом числа элементов и при =6 более 1:3 (3 – 10 ГГц).

 

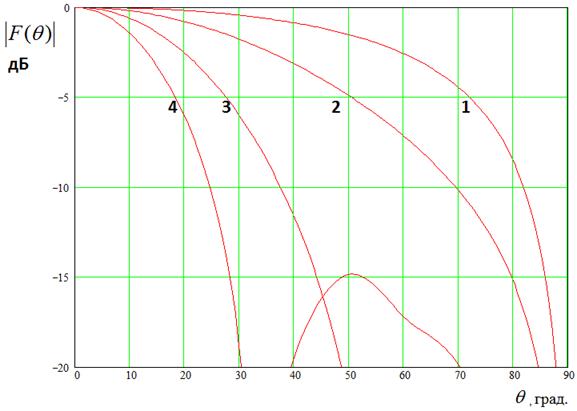
Рис. 11. ДН подрешетки из трех элементов

Трансформацию ДН подрешетки можно видеть на рис. 11, 12, на которых показаны ДН подрешеток из трех  и шести элементов, соответственно. Кривые 1 - 4 получены, соответственно, для 0.5, 4, 8, 12 ГГц. Видно, что на низких частотах ДН подрешетки мало отличается от ДН одного элемента. Такое положение наблюдается вплоть до частот, на которых размер подрешетки  сравнится с половиной длины волны в свободном пространстве. После этого ДН начинает сужаться. Влияние резонансных эффектов сказывается в узких диапазонах частот. Поэтому они не видны на рис. 11,12.

 

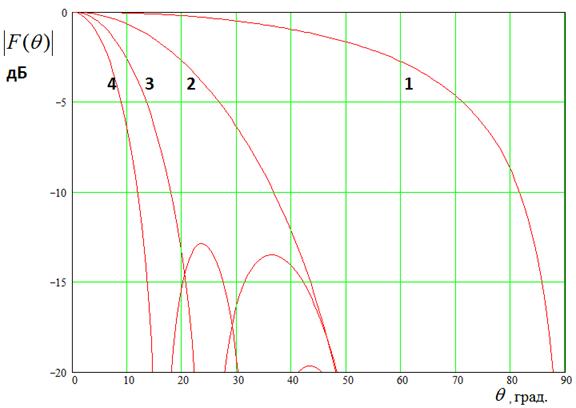
Рис. 12. ДН подрешетки из шести элементов

На рис. 13 показана ДН подрешетки из трех элементов на частоте 11.9 ГГц. На ней хорошо виден провал в районе 10⁰, искажающий форму ДН и снижающий коэффициент направленного действия.

На рис. 14 кривые 1 - 5 показывают зависимость ширины ДН по уровню – 10 дБ  от частоты для  кластерного облучателя с соответствующим числом элементов. Меняя число элементов в кластере в зависимости от частоты можно обеспечить почти постоянное значение ширины ДН. Как видно на рис. 14, полоса частот кластера из 2-5 элементов с шириной ДН 100 градусов   при этом составит величину порядка 1:3 (от 3.5 до 9.5 ГГц). Для уменьшения скачка ширины ДН при изменении числа элементов в кластере, добавление нового элемента в кластер следует производить с переменным весом.

 

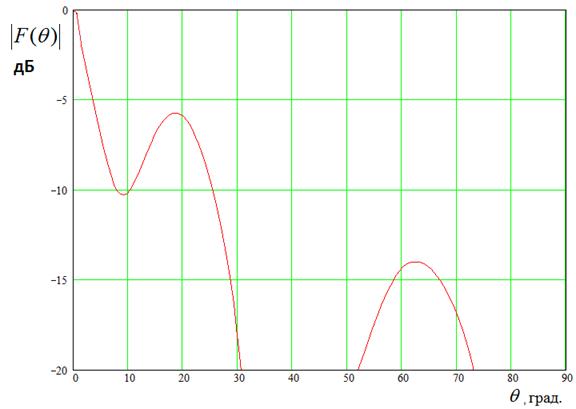
Рис. 13. ДН подрешетки из трех элементов на частоте 11.9 ГГц

 

 

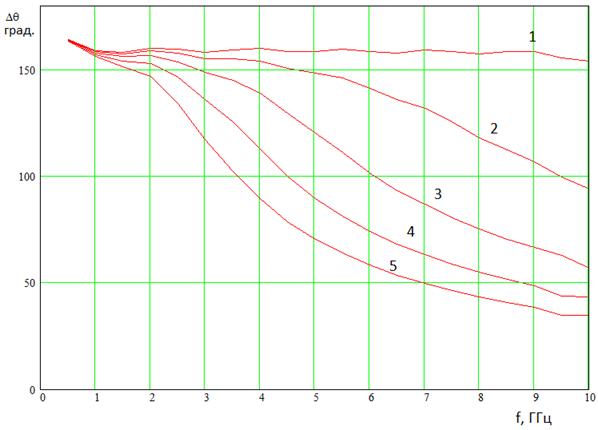
Рис.14.Зависимость ширины ДН кластерного облучателя от частоты

 

Заключение

Из полученных в работе результатов, можно сделать следующие выводы:

1.     Полоса частот согласования  кластерного облучателя растет пропорционально числу элементов кластера.

2.     Полоса частот, в которой можно обеспечить стабильность ширины  диаграммы направленности кластерного облучателя за счет изменения числа его элементов растет пропорционально числу элементов кластера

3.     Полоса частот кластерного облучателя в виде линейной решетки из 5 антенн Вивальди при уровне согласования -15 дБ и ширине диаграммы направленности 100 градусов составляет величину порядка 1:3.

Реализация схемы построения системы для обеспечения режима изменения числа элементов кластера в зависимости от частоты требует отдельного исследования и выходит за рамки данной работы. Очевидно, что наиболее просто такой режим можно обеспечить в многолучевой гибридной антенне с цифровой обработкой сигналов.

 

         Работа выполнена при поддержке РФФИ, проект №15-07-07797.

 

Литература

1. Ghavami M., Michael L.B., Kohno R. Ultra Wideband Signals and Systems in Communication Engineering // John Wiley & Sons, Ltd. 2007.

2. В.А.Калошин, Многолучевые гибридные антенны, Труды 13 Междун. Крымской конф.  «СВЧ техника и телекоммуникационные технологии», Crimico-2003, Севастополь, сентябрь, 2003, с.383-390.

3. Park Y.-J. and Wiesbeck W. Offset cylindrical reflector antenna fed by a parallel-plate Luneburg lens for automotive radar applications in millimeter-wave // IEEE Trans. Antennas Propag., vol. 51, no. 9, pp. 2481-2483, Sep. 2003.

4. Бирюков В. Л., Ефимова Н. А., Калиничев В. И., Калошин В. А., Пангонис Л. И. Исследование сверхширокополосной кольцевой антенной решетки // Журнал радиоэлектроники [электронный журнал]. 2013. № 1. URL: http://jre.cplire.ru/mac/jan13/20/text.html.

5. Yang Y., Wang Y., and Fathy A.E. Design of a compact Vivaldi antenna arrays for UWB. See through wall applications // PIERS 82, p.p. 401–418, 2008.

6. Chang J., Schaubert D.H., Yngvesson K.S., Huang J., Jamnejad V., Rascoe D., Riley L. // IEEE AP Symp. Proc. 1990. USA Dallas. P. 1150.

7. Воскресенский Д. И., Котов Ю. В., Овчинникова Е. В. // Антенны. № 11(102). 2005. С. 7.

8. Амитей Н., Галиндо В., Ву Ч. Теория и анализ фазированных антенных решеток // М.: Мир. 1974.

9. С.Е. Банков, М.Д. Дупленкова. Модель бесконечной решетки бегущей волны в виде канала Флоке // Труды международной НТК ИРЭМВ – 2013. Россия, Дивноморское, 24-28 июня 2013. С. 194-198.