"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 2, 2002

оглавление

дискуссия

 

Воздействие мощного излучения СО₂-лазера на крупные капли воды, ледяные кристаллы сферической формы и атмосферные осадки
 

В.К.Рудаш.

 

ИРЭ РАН, г. Фрязино.

 

 

 

Получена 15 февраля 2002 г.

 

        Экспериментально исследованы режимы испарения крупных капель, воды и сферических частиц льда. Обнаружены два режима испарения водяных капель (конвективный с выбросами пара и взрывной), два режима испарения кристаллов льда сферической формы (плавление-испарение водной капли и взрыв). Обнаружен многократный взрыв капель воды. Система двух уравнений с высокой точностью представляет решение исходной системы уравнений и описывает экспериментальные ре­зультаты. Проанализированы результаты экспериментальных исследований по распространению мощного излучения CO₂ - лазера в искусственных и естественных туманах, снегопадах. Основное внимание уделено изучению особенностей теплового метода воздействия на водный аэрозоль. Описаны методика и результаты определения основных параметров, характеризующих процесс просветления  искусственного  тумана кольцевым пучком мощного СО₂  - лазера. Принятая теоретическая модель просветления водного аэрозоля правильно передает основные особенности процесса. Показано, что при просветлении тумана в натурных условиях существенна роль бокового ветра на процесс замывания канала. Приведены коэффициенты ослабления излучения CO₂ – лазера во влажном снеге в зависимости от интенсивности снегопада.

 

1.    ВВЕДЕНИЕ

2.    ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЖИМЫ ИСПАРЕНИЯ КАПЕЛЬ ВОДЫ И КРИСТАЛЛОВ ЛЬДА

3.    Искусственный туман

4.    Естественный туман

5.    Снег

6.    СПИСОК   ЛИТЕРАТУРЫ

7.    рисункИ

 

 

1. ВВЕДЕНИЕ

 

           В 70-х – 80-х годах XX в. было опубликовано большое число теоретических и экспериментальных работ по вопросам распространения  и  теплового самовоздействия лазерных пучков в  атмосфере. В целом ряде монографий (например в [1-3]) обобщены результаты моделирования  и  теоретического  анализа самовоздействия в турбулентных, аэрозольных и облачных средах.  В работе [4]  была разработана модель распространения интенсивного лазерного пучка в водном аэрозоле в условиях одновременного проявления эффектов просветления и теплового самовоздействия. При этом большинство имеющихся данных были получены в  экспериментах со сравнительно маломощными источниками излучения. Данная работа является одной из немногих, посвященных проблеме распространения мощного (до 16 кВт) излучения CO_2- лазера в атмосфере, содержащей водный аэрозоль. Она является продолжением экспериментальных и теоретических работ, которые были начаты в конце 60-х годов в ИРЭ РАН под руководством профессора М.А.Колосова.

        При распространении интенсивного лазерного излучения в аэрозольной  среде  часть  энергии,  поглощенная  частицами среды, вызывает их нагрев и последующее испарение. Исследования показали, что в зависимости от интенсивности воздействующего излучения, времени воздействия, размеров капель реализуется регулярный (испарение) или взрывной режимы разрушения аэрозолей [5-6].  Анализ эволюции ле­дяных частиц (пластинка и сфера) экспериментально изу­чался в работах [7-8]. Изучение теплового взаимодействия пучка излучения с аэрозольными частицами удобно проводить с поглощающими каплями большого размера (радиус от 0,1 до 1 мм). В этом случае проще осуществить подвес капель, измерение их размеров и скоростей испарения, чем в случае капель с радиусом в единицы микрометров, а также легче реализовать различные режимы испарения, т. е. интервалы изменений размеров частиц и интенсивно­сти, в пределах которых преобладает тот или иной теп­ловой механизм испарения: диффузный, конвективный, взрывной.

        В [9] установлен критерий, определяющий смену режимов испарения для малых капель: wK_пR = const, где w – интенсивность излучения; R - ра­диус частиц; K_п - фактор поглощения излучения части­цей. Получены аналитические зависимости скорости  испарения от интенсивности и размера частиц для каждого режима. На основе этого анализа был вначале предска­зан теоретически [10], а потом подтвержден эксперимен­тально [11-12] режим взрыва водяных капель.

     Просветление среды в регулярном режиме происходит при относительно невысоких интенсивностях излучения  w=10²…10⁴ Вт/см². При воздействии импульсного излучения на водный аэрозоль (w = 10⁵…10⁶ Вт/см² ) наблюдаются свои особенности, связанные с переходом от регулярного испарения к взрывному  разрушению капель [13]. Скорость  образования просветленной зоны и ее размеры определяется временной  зависимостью коэффициента объемного ослабления излучения  аэрозольной средой. Скорость испарения капель в определенной точке пространства определяется интенсивностью излучения в этой точке. Профиль температурного поля в  канале определяется начальным распределением интенсивности в пучке  и явлениями переноса, т. е. действием ветра и  наведенной  конвекции. Неравномерный по сечению пучка нагрев среды приводит к  образованию тепловых  воздушных неоднородностей,  непрерывно  распределенных  по   длине пучка. Эти неоднородности оказывают влияние на условия распространения лазерного излучения в зоне просветления. 

      Степень теплового самовоздействия пучка определяется соотношениями между тремя линейными масштабами: характерной длиной теплового самовоздействия, обусловленной молекулярным поглощением в насыщенном водяном паре – L_T , характерной длиной теплового самовоздействия, обусловленной теплопотерями испаряющихся капель- L_T^о, и характерной длиной просветления – L_пр  [3,4]. Важнейший масштаб - масштаб нелинейного взаимодействия пучка с аэрозолем  L_a  = g_о^-1. Он же определяет ослабление излучения в линейной среде. Ниже даются оценки этих масштабов для данной работы.

    Цель данной работы - эксперименталь­но изучить режимы испарения закрепленных капель воды и ледяных кристаллов сферической формы с радиусом порядка 1 мм при воз­действии на них  лазерного излучения с длиной волны 10,6 мкм; исследовать динамику просветления искусственного и естественного тумана излучением  СO₂-лазера с мощностью 12…16 кВт и 1 кВт соответственно, а также ослабления излучения с мощностью 1 кВт в снегопадах на трассе протяженностью 760 м.

 

 

 

2. ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЖИМЫ ИСПАРЕНИЯ КАПЕЛЬ ВОДЫ И КРИСТАЛЛОВ ЛЬДА

 

Методика измерений. Эксперименты по воздействию ИК излучения на капли H₂O и сферические частицы льда с радиу­сами порядка 1 мм проводились при интенсивностях 20-10⁴ Вт/см²  по известной методике [12].

Источником когерентного излучения служил непрерывный СО₂-лазер с мощностью 1 кВт. Капли H₂O подвешивались на нити из стекловолокна диамет­ром 60-80 мкм. Ледяные частицы получались в резуль­тате замерзания капель воды с радиусом 1 мм, кристал­лизация капель происходила за время порядка 5 мин. Температура воздуха в период замерзания была -2... -4°С. Изменение размера  капель H₂O и сферических частиц льда регистрировалось в проходящем свете при помощи кинокамеры СКС-1М-16 со скоростью 800-4000 кадр/с, соединенной с микроскопом МБС-2. Для перекрытия пучка применялся магнитный затвор с временем пере­крытия 0,03 с. Синхронизация момента воздействия излучения и начала съемки осуществлялась с помощью реле времени, а диаметр капель измерялся компарато­ром ИЗА-2. Всего было проведено 100 опытов по испаре­нию капель H2O и частиц льда, начальный радиус которых был близок к 1 мм.

 

Режимы испарения капель воды. Диффузионное испа­рение водяной капли в поле излучения характеризуется малым давлением насыщенного водяного пара на по­верхности капли по сравнению с атмосферным. Повы­шение мощности падающего на каплю излучения сопро­вождается возрастанием поверхностного давления водя­ного пара с возникновением конвективного или стефановского течения воздушно-паровой смеси. Для описа­ния конвективного режима испарения необходимо учи­тывать как диффузионный, так и стефановский потоки водяного пара [14]. Теоретические исследования показали, что система уравнений вида [14,15]

 

        ,                                                 (1)

    

        +                                                                        (2)

                   

действительно определяет радиус конвективно испаряю­щейся капли с относительной погрешностью не более 5%. В уравнениях (1) и (2)  l₁   - теплопроводность воздуха; r₂,   l₂,c₂   - соответственно плотность, теплопроводность и теплоемкость воды; T_пов — температура поверхности капли; T₀ - ее начальная температура; q(T₀) — удельная теплота парообразования; c_p- теплоемкость водяного пара при постоянном давлении; r_н — плотность насыщен­ного водяного пара; r₀ = r_н(T₀); D - коэффициент вза­имной диффузии пара и воздуха; J_T - среднеарифметиче­ская скорость молекул пара; a - коэффициент конденса­ции; K_п ( R, l, m) - эффективность поглощения излучения на длине волны l каплей радиуса R с комплексным показателем преломления m = n –iж..

    Анализ экспериментальных результатов показал, что в исследованном интервале w можно выделить три подинтервала, в каждом из которых испарение капли обла­дает своими особенностями. При w = 30-200 Вт/см² радиус капли изменяется по закону, близкому к линей­ному, а выделение пара происходит равномерно со всей поверхности. Экспериментальные зависимости радиуса капли для этого случая показаны на рис.1. Здесь же приведены решения уравнений (1) и (2) для значений параметров, реализовавшихся в экспериментах, с уче­том ошибок измерений.

    Из рис.1 видно, что уравнения описывают законо­мерности испарения крупных водяных капель под воз­действием излучения СО₂ - лазера, включая и переходный процесс. Например, при w = 40 Вт/см² установление постоянной скорости испарения происходит через интер­вал времени t = 0,5 с после начала воздействия излучения, который определяет, очевидно, время переходного процесса для испарения капли в конвективном режиме. Если интенсивность была больше 200 Вт/ см², процесс испарения капли характеризовался интен­сивными выбросами пара навстречу воздействующему излучению, в промежутках между которыми радиус уменьшался также линейно. Средняя продолжитель­ность выбросов пара составила 0,01 с, перед очередным выбросом капля принимала сферическую форму. На­блюдаемые выбросы объясняются образованием и по­следующим ростом пузырьков перегретого пара на го­товых центрах парообразования (гетерогенная нуклеация), всегда присутствующих в воде в виде примесей. Наличие выбросов не может, однако, существенно изме­нить энергетический баланс капли, поэтому ее радиус по-прежнему определяется соотношениями (1) и (2).

    На рис.2 результаты экспериментов сравниваются, в частности, с приближенным решением задачи об испарении крупных водяных капель [16-18], когда временная зависимость радиуса капли описывается выражением

 

,                (3)

где

                         ,

- температуропроводность воды. Нетрудно видеть что формула (3) удовлетворительно описывает только наклон экспериментальных зависимостей в кон­вективном режиме для w = 76 Вт/см², а также при наличии выбросов пара для w = 480 и 1650 Вт/см². Дли­тельность переходного процесса, следующая из урав­нения (3), теперь меньше экспериментальной. При w > 500 Вт/см² наблюдается взрывной режим испарения капли, который в целом характеризуется ее взрывом через некоторое время t_взр  после начала воздействия. При этом изменения режима испарения в интервале 0 £ t  £ t_взр различны для 500 < w < 2000 Вт/см² и w > 2000 Вт/см².

    В первом случае испарение капли до t_взр  сопровожда­ется интенсивными выбросами пара и мелких капель, радиус капли в момент взрыва составлял (0,6-0,9) R₀. Например, при w = 500 Вт/см² в опыте наблюдалось 12 интенсивных выбросов пара, после чего капля взорва­лась (t_взр = 0,47 с). При рассматривании процесса испаре­ния на кинопленке видно, что выбросы пара напоминают поверхностные взрывы, их можно отождествить с выходом пузырьков пара на поверхность капли.

В таблице 1 приведен ряд параметров, характеризую­щих процесс испарения капель при 500 < w < 1000 Вт/ см².    Параметр g представляет собой отношение энергии, поглощаемой каплей за время  (время уста­новления температурного поля в объеме капли), к энер­гии, необходимой для испарения капли на начальном этапе испарения. В конвективном режиме параметр g в экспериментах был порядка единицы.

 

Табл. 1

w, Вт/см2	R0, мм	g	tвзр , с	dR/dt|tвзр,, мм/с	R(tвзр ), мм
500	1,24	12,1	0,47	0,42	1,06
880	0,87	15,0	0,51	1,03	0,72
990	1,12	21,6	0,27	1,25	1,04

 

Во втором случае взрыву капли предшествует ее не­которое расширение. При w > 2000 Вт/см² в предшест­вующие взрыву моменты времени радиус изменяется аналогично тому, как показано на рис.3. С увеличением интенсивности излучения t_взр уменьшается, а частота выбросов и мелких капель возрастает. При w = 10⁴ Вт/см² имеем  t_взр = 0,05-0,06 с.

    Представляет интерес многократный взрыв капли при w = 10⁴ Вт/см² и диаметре пучка 10 мм. В этих опытах применялся быстропроточный СО2-лазер с мощ­ностью 10 кВт [19]. В одном из опытов капля с  R₀= 1,5 мм взорвалась через t = 0,056 с после начала дефор­мации. В процессе взрыва образовалась вторая капля с радиусом 0,7 мм, которая двигалась со скоростью 20 см/с. После первого взрыва произошел отрыв капли от нити. Капля приняла сферическую форму и через t = 0,008 с, после отрыва свободная капля взорвалась вторично. Общее время, в течение которого имел место двукрат­ный взрыв, составило 0,098 с. На рис.4 приведены фото­графии взрыва свободной капли.

    Измеренные значения  dR/dt в интервале w = 40-500 Вт/см² можно аппроксимировать линейной зависимостью вида

          ,                                               (4)

найденной методом наименьших квадратов. Здесь  dR/dt  взято в миллиметрах в секунду, а w - в ваттах на квадратный сантиметр.

    Полученные результаты позволили найти зависи­мость времени испарения капли t_исп от интенсивности в интервале w = 40 — 10⁴ Вт/см² в предполо­жении, что измеренные величины  lgt_исп  и  lgw   связаны линейной зависимостью:

            ,                                                                       (5)

где w берется в ваттах на квадратный сантиметр, а  t_исп - в секундах.

    Эксперименты показывают, что постоянная скорость изменения радиуса капли устанавливается спустя неко­торый промежуток времени t_п после начала воздействия излучения. В рассматриваемом интервале значений w время t_п ( меняется от 0,5 до 0,02 с. Измеряя  t_п, можно оценить повышение средней температуры капли Т за время переходного процесса:

.                                                      (6)

При  w > 7-10³ Вт/см² температура в конце переход­ного процесса может достигать критической температу­ры взрывного кипения воды, равной 578 К. В действите­льности, как это и наблюдалось в опытах, взрыв капли может происходить при меньших w, поскольку из-за больших размеров капель поглощаемая ими энергия выделяется в малой части объема капли, где и возможно достижение критической температуры.

Представляет интерес оценить КПД процесса испаре­ния капли, определяемый выражением

            ,                                                                                 (7)

где  t₁ - время измерений R(t) в отдельном опыте. Сред­ний КПД  h_ср  оказался равным 70% для конвективного режима испарения и 35% для конвективного режима с выбросом пара.

 

Режимы испарения сферических ледяных частиц. Ана­лиз кинограмм процесса испарения показал, что в иссле­дованном интервале значений w наблюдались два раз­личных механизма испарения частиц. При действии пер­вого из них частица вначале плавится, а затем образо­вавшаяся капля конвективно испаряется по линейному закону, аналогичному показанному на рис.1. Такое испа­рение, которое также можно назвать конвективным, реа­лизуется при wR₀K_п(R₀, l, m) » 30-500 мм Вт/см². На рис.5 приведен пример экспериментальной зависимости R(t для сферической частицы с  R₀» 1 мм, полученный при w = 30 Вт/см². Там же для сравнения даны найденная в этой серии опытов экспериментальная зависимость R(t) для водяной капли с тем же начальным радиусом и тео­ретическая временная зависимость радиуса капли, следующая из уравнений (1) и (2).

    Можно видеть, что скорости испарения ледяной час­тицы и водяной капли практически совпадают. Различие в наклоне теоретической зависимости радиуса капли и экспериментальной зависимости R(t) равно 9% и на­ходится в пределах погрешности измерений w, состав­ляющей ± 15%. Таким образом, испарение расплавлен­ной ледяной частицы происходит со скоростью, которую можно найти по формулам (1) и (2). Из рис.5 следует еще одна особенность процесса испарения ледяной частицы: кривая R(t) для нее сдвинута по оси времени относи­тельно аналогичной кривой для водяной капли на неко­торый интервал. Этот сдвиг определяется временем, необходимым для плавления частицы:

 ,                                                                                                     (8)

где r_l, q_пл - плотность и удельная теплота плавления льда. В рассматриваемом случае  t_пл = 1,4 с, что хорошо согласуется с данными эксперимента. Анализ результа­тов показал, что при плавлении объем ледяной частицы уменьшается на 8% (а ее радиус на 3%).

    В опытах с  w= 500 Вт/см² ледяная частица плавилась за время 0,1 с. Далее процесс испарения сопровождался интенсивными выбросами пара и мелких капель, дли­тельность одного выброса составляла 0,01с.

    При wR₀ > 500 мм Вт/см² наблюдался взрывной ре­жим испарения частицы. Кинограммы показывают, что разрушение частицы происходило в этом случае путем последовательного образования и разрушения пузырей пара на облучаемой части поверхности. Размеры об­разующихся пузырей сравнимы с размерами частицы. Когда пузырь лопается, от частицы навстречу воздей­ствующему излучению вылетают мелкие капли. Число их значительно больше числа капель, образующихся при взрывном испарении водяной капли. Кроме того, при взрыве ледяной частицы пузырь пара образуется и лопается за более короткое время (0,001-0,0025 с), чем в случае водной капли (0,01 с).

    При интенсивности излучения w = 1400 Вт/см² ледяная частица с R₀= 1 мм полностью разрушилась за время 0,13 с, в течение которого на ее поверхности об­разовалось 15 пузырей пара. При w = 4000 Вт/см² время полного разрушения частицы составило 0,09 с. Оценки показывают, что взрывной режим испарения ледяной частицы наступает при таких w, при которых время плавления частицы становится сравнимым с характер­ным временем выравнивания температуры внутри нее где см² с^-1 - температуропро­водность льда. С физической точки зрения это совер­шенно естественно, так как при t _l >  t_пл кипение воды на облучаемой стороне поверхности частицы наступает раньше, чем поглощаемая частицей энергия поступит в ее неосвещенное полушарие.

    Таким образом, система уравнений (1) и (2) с высокой точностью представляет решение исходной системы уравнений и хорошо описывает экспериментальные ре­зультаты в области диффузионного и конвективного испарения водной капли в радиационном поле.

   В работе [20] исследуется модель распространения интенсивного лазерного излучения в атмосферных осадках. На основе взаимодействия импульсного лазерного излучения (l = 0,69 мкм) с отдельной крупной каплей (R = 50 - 200 мкм) показано, что осадки  под воздействием интенсивного излучения  ~ 10⁶ Вт/см², обеспечивающего взрыв водяных капель, трансформируются в туман средней плотности. Условия распространения излучения в этом случае резко ухудшаются.

 

 

 

3.   Искусственный туман

 

Методика измерений. Экспериментальные исследования  просветления искусственных туманов под воздействием ИК-излучения с мощностью 12 - 16 кВт проводилось в камере (камера ИТ). Объем камеры был  3,8   м³, длина - 4,8 м. Туман создавался путем  распыления  воды  сжатым воздухом. Анализ спектров капель показал, что размеры капель в  тумане изменялись в  пределах от 1 до 30 мкм, средний размер составил 5 мкм, туман распадался за время 12 - 15 минут. 

    Схема установки для исследования приведена на рис.6. В качестве источника излучения применялся быстропроточный CO₂ - лазер [19]. Зеркалами 2, 3, 4, 5 мощное излучение направлялось  на  камеру  ИТ. Зеркало 2 является калориметрической нагрузкой измерителя мощности. Через отверстие в зеркале 5 диаметром 3 мм проходил зондирующий луч от гелий-неонового лазера 6. С помощью зеркал 3, 4, 5 центры пучков излучений на  l = 0,63 мкм и  l = 10,6 мкм совмещались.  На  приемном конце трассы мощное излучение отражалось от зеркала 13 на  поглотитель 16, а зондирующий луч проходил через отверстие диаметром 6  мм в зеркале 13, кварцевую пластину 14  на  фотодиод  15  типа  ФД-7К. Излучение второго He-Ne - лазера 9 применялось как опорное при прохождении просветляющего пучка через аэрозоль, параметры которого непрерывно контролировались на волне 0,63 мкм. Оно фокусировалось зеркалом 18 на фотоумножитель 19 типа ФЭУ-22. Лазерные пучки на l  = 0,63 мкм модулировались с частотой 1000 гц с помощью механических модуляторов 7, 10. Для усиления сигналов с  ФЭУ-22 и ФД-7К применялись усилители типа У-2-6. Сигналы с двух усилителей поступали на НЧ-детектор 22  и  регистрировались  быстродействующим самописцем 23 типа Н-320-5. 

Расстояние между опорным и зондирующим лучом на волне 0,63 мкм было 37 см. Диаметр пучка мог изменяться перемещением зеркал 2  и  3 относительно камеры. Определение геометрических размеров пучка проводилось путем прожигания мелкой  металлической  сетки. При  оценке интенсивности излучения воздействующего на туман излучения учитывалась  кольцевая геометрия пучка: толщина кольца была 10 мм, внешний диаметр  кольца составлял 45; 60; 65 мм, внутри кольца был  провал интенсивности (на эту область приходилось ~5% мощности излучения).  В этом случае в центральной части пучка мог образовываться отрицательный радиальный градиент показателя преломления, и, следовательно, интенсивность  зондирующего излучения вблизи оси  пучка  могла возрастать.

    Измерения коэффициентов ослабления зондирующего и опорного излучений проводились одновременно. Продолжительность измерений определялась временем воздействия мощного ИК -  излучения  на  туман  и составляла 8 - 35 с. Коэффициент ослабления   на    l =  0,63  мкм вычислялся по формуле: 

                                                     ,                                       (9)

где I₀  - интенсивность принимаемого излучения в случае чистой атмосферы, l - длина траектории пучка в тумане. По измеренным  коэффициентам ослабления на волне 0,63 мкм  определялась  метеорологическая дальность видимости S_m , водность q, а также коэффициент  ослабления на волне 10,6 мкм до воздействия на туман мощного излучения [21]: 

S_m = 3,912 [R1] / g, ;   q (г/м³) = 4,76 g [R2] ;  g_10,6 = 0,43 g_{0,63  .}         (10)

    Значения h принималось значение равное 0,43, и считалось, что величина h определяет отношение не только начальных оптических толщин для излучения l = 0,63 и 10,6 мкм, но и отношение конечных оптических толщин уже в просветленной зоне.

    Относительная степень просветления тумана вычислялась  по формуле: 

                                                                             (11)

где  t(о) = g_оп l  - оптическая толщина для излучения на   l = 0,63 мкм вне канала  (опорное), t(k) =  g _k l  - оптическая толщина для излучения на  l  =  0,63 мкм в канале (зондирующее). 

    Важными характеристиками, определяющими эффективность теплового метода просветления водного аэрозоля интенсивным лазерным излучением, являются время и скорость просветления аэрозоля. По данным измерений времени просветления t_пр   определялась средняя скорость просветления V_пр в зоне воздействия длиною 4,8 м (V_пр = 4,8/ t_пр).     Вычислялась также средняя  скорость  уменьшения  коэффициентов  ослабления опорного излучения - V_Dg = Dg / Dt.

 

Экспериментальные результаты. Особенностью экспериментальных данных является то, что они получены в условиях, когда одновременно проявлялась целая группа эффектов, которые могут сопровождать распространение пучка в аэрозольной среде. Прежде всего это эффекты тепловой фокусировки, дифракционной расходимости, ослабления и просветления. В случаях, представляющих практический интерес, значительные искажения геометрии пучка на приземных трассах достигаются на расстояниях, которые на порядок величины меньше дифракционной длины L_д = ka² [1- 4]. Для  l  = 10,6 мкм и  радиуса  пучка  а » 3 см    L_д » 530 м.

    Коэффициент ослабления излучения на  l   =  0,63  мкм  в начальный момент воздействия мощного излучения на l  = 10,6 мкм  лежал в пределах от 1,6 до 2 м ^-1, что соответствовало  оптической толщине тумана  t₀ от 7,5 до 10, водности q₀ от 7 до 9,9 г/м³,  метеорологической дальности видимости S_m от 1,9 до 2,5 м, коэффициенту ослабления излучения  g_10,6  от  0,7  до 0,9 м ^-1. Водность естественных туманов составляет от  0,02  до 1 г/м³ .

     На рис.7а,б приведен пример записи  интенсивности  сигналов зондирующего I_з  и опорного излучения I_оп, соответствующей  начальному   моменту воздействия излучения,  где  P  =  13,6  кВт,      w_вх = 1 кВт/см²,  D_вх  = 65 мм,  t_возд = 8 с.  В центре кольца интенсивность излучения была ~ 100 Вт/см². Если принять участок линейного нарастания интенсивности сигнала  I_k  равным  времени образования  канала, то t_обр  = 0,35 с и скорость  прорастания канала составила V_k »13,7 м/с. Степень просветления    dt =  99,7%  достигалась через 2 с после начала воздействия. При этом  L_пр = 4,8 м.

    Оценим характерные длины теплового самовоздействия, обусловленные молекулярным поглощением в насыщенном водяном паре и теплопотерями испаряющихся капель соответственно по формулам [22]:

,                                              (12)

  .                                                   (13)

Здесь а – радиус пучка, c_p и r - теплоемкость при постоянном давлении и плотность воздуха, a₀ - коэффициент молекулярного поглощения водяного пара, V- скорость конвективного переноса среды,  DT – максимально возможное приращение температуры среды из-за теплопотерь капель. Для атмосферы dn/dT ~ 10^-6 К^-1 и параметр DT при условии полного испарения аэрозоля при концентрации 10³см^-3, согласно результатам численного расчета [23], имеет величину ~ 6,4^о С. Подставляя в формулы (4-5) численные значения параметров: P = 16 кВт,  r =1,3× 10^-3 г×см ^-3 , c_p  = 0,24 кал×г^-1× K^-1, a = 5×10^-6см^-1, V = 6 см/с получаем значения линейных масштабов для экспериментов в камере ИТ:  L_пр = 4,8 м,  L_Т^о = 11,9 м,  L_Т = 18,6 м. Соотношение между ними удовлетворяет неравенству L_пр <  min (L_Т^о , L_Т) и позволяет сделать вывод о том, что  следует ожидать незначительного влияния тепловых искажений и расчеты просветления водного аэрозоля лазерными пучками можно проводить без учета эффекта теплового самовоздействия [4]. Масштаб нелинейного взаимодействия пучка с аэрозолем  в начале воздействия на туман составлял  L_a = 1,2 – 1,4 м.

    Оценим время образования канала на  l  = 10,6 мкм. В приближении Гликлера [24], время  достижения заданного  уровня прозрачности T_10,6  в неподвижной облачной среде с начальной оптической толщиной t_10,6           определяется выражением [2]: 

 ,                                         (14)        

где C = 3A₀b_Tb_p /4rL,  b_p=1/(1+0,65A₀R₀₂), A₀ - коэффициент пропорциональности в выражении K₀ = A₀R, определяющем зависимость фактора эффективности ослабления излучения от радиуса капель R,  справедливом для капель с R <   l₀ = 10,6 мкм, b_T - коэффициент,  учитывающий потери энергии излучения на нагрев среды при испарении капель, b_p - коэффициент, учитывающий потери энергии излучения на рассеяние каплями, r  и  L- плотность  и удельная теплота парообразования воды, R₀₂  -  среднеквадратичный радиус  капель, w – интенсивность излучения на оси пучка. При этом отношение  начальных  оптических  толщин  на  волнах 10,6 и 0,63 мкм определяется выражением:

,                                           (15)      

где R₀₂  и  m – параметры начального  гамма–распределения капель по размерам. 

    В процессе испарения тумана связь между его оптическими толщинами приближенно можно записать в виде [25]: 

                        .                                                (16)

Для модального радиуса капель R_m =  4 мкм,  m  =  6 согласно [25] получаем:   w₁  = 1,48; w₂ =  2. Для параметров, входящих в формулы  (6 - 8):  w  =  100 Вт/см²;      t_0,63(0) = 9,6; A₀  = 2000 см^-1 ; h₀  =  0,6;    b_T = 0,75  (T   =  20⁰ C); R_m = 4 мкм и   m = 6; b_P = 0,6; T_0,63  = 0,9; T_10,6  =  0,99  получаем, что время просветления на   l = 10,6 мкм  составляет  величину  t  »   0,35 с. Согласие экспериментального и теоретического времени просветления в центре кольцеобразного пучка можно считать удовлетворительным.

          В [2] представлены данные о зависимости нормированной скорости просветления V_пр   облачной среды от интенсивности излучения в пределах от 50 до 2500 Вт/см², полученные на основании измерений времени просветления  по центру пучка CO₂ - лазера на трассах от 1 до 9 м при коэффициенте ослабления g₀ от 0,15 до 1,2 м^-1 . Экспериментальные результаты  согласуются с теоретическим представлением о линейной зависимости  V_пр  от w₀ в широком диапазоне изменения w₀, для которого реализуется диффузионный (регулярный) режим испарения капель.

       Согласно (6) можно оценить время и скорость просветления на   l = 10,6 мкм в пространстве самого кольца, где интенсивность примерно на порядок выше:  для w₀  »  1000     Вт/см²  соответственно получим  t » 0,035 с;      и    V  »  4,8 / 0,035  » 137 м/с. 

     Оценим КПД процесса просветления, определяемый как отношение энергии, необходимой для испарения капель в просветленной зоне (длиной l и поперечным сечением  S), к энергии излучения лазера, поступившей в зону за время ее просветления по соотношению

                              h = L₁DqS l / (w₀S t_пр) = L₁DqV_пр / w₀,                           (17)

где     L₁ = L + cDT⁰ ,L = 2260 Дж/г – удельная теплота парообразования; с = 4,2 Дж/г×град – удельная теплоемкость воды; DT⁰ – изменение температуры аэрозольной среды при ее нагреве; Dq = q₀­ - q_k – изменение водности аэрозоля при его просветлении; q₀, q_k – соответственно начальная и конечная водность аэрозоля в просветленной зоне. Величина  Dq определялась с помощью соотношения

                                     ,                                          (18 )

 где    и      - начальный и конечный коэффициенты ослабления в просветленной зоне, измеренные на l_з = 0,63 мкм; k_q –коэффициент соответствия, связывающий коэффициент ослабления g_0,63 с водностью тумана q и зависящий от его микроструктуры  g_0,63 = k_q × q. Для усредненных экспериментальных оценок h  было выбрано значение  k_q = 0,18 м²/г  и  m = 4 [26]. Подставляя в (9–10) параметры:  DT⁰ = 6,4 ⁰С;   = 2,08 м^-1;   = 0,13 м^-1  Dq =10,83 г/м³; V_пр = 137 м/с, w₀ = 10³ Вт/см ²   получаем  h = 33,9 %. Относительно величины КПД в работе [26]  сделан вывод: что экспериментальное значение h » 33 % характеризует КПД теплового метода просветления облаков и туманов в отсутствие ветра во всем возможном диапазоне изменений их температуры.  При этом численные расчеты  КПД были выполнены при w₀ ³ 10³ Вт/см ² и T₀ = 253-293 К. В работах  [5,12] нами установлено, что экспериментальное значение КПД процесса испарения водной капли с радиусом 1 мм в конвективном режиме при w =2×10² - 10³ Вт/см ² составляет ~ 35 %. Таким образом, можно сделать вывод, что в регулярном режиме на испарение капли или ансамбля  капель расходуется ~ 1/3 часть энергии воздействующего излучения.

      На рис.8 а и б показана временная зависимость процесса  замывания зоны просветления туманом после прекращения действия  излучения CO₂  - лазера.   Для мощности воздействующего  излучения P = 13,65 кВт, средней интенсивности излучения w = 1 кВт/см² , внешнего диаметра кольца D = 60 мм и начальной оптической толщины  t = 10 время замывания зоны просветления составило  t_зам » 0,5 с. Оценка средней скорости конвективных потоков среды, замывающих канал с радиусом  a »3 см дает величину V_k » 6 см/с.  Согласно теории размерностей, установившаяся скорость конвективного всплывания среды в лазерном пучке равна [27]:

                                                                                           (19)

и не зависит  от радиуса пучка. Подставляя в последнюю формулу (11) численные значения параметров: P = 13,65 кВт, a = 5×10^-6см^-1, T₀ = 293 K находим, что V_g » 4,8 см ×с^-1. Эта величина согласуется с оценками скорости наведенных движений, реализовавшейся в камере. Степень влияния наведенной конвекции на тепловую дефокусировку  определяется вкладом механизмов теплопроводности и конвекции в охлаждение области пучка. Время нахождения капель в области пучка равно t_k= 2a/V_k ~ 1 с.  Влияние теплопроводности на формирование температурного поля в области пучка определяется характерным временем t_m = a₂/(4a₁²), где а₁² = l₁/c_pr - температуропроводность среды, равная для воздуха при нормальных атмосферных условиях ~ 0,18 см²×с^-1.  Для условий опытов характерное время выравнивания температуры среды вследствие теплопроводности  t_m » 12 с. Это означает, что перегрев области пучка над окружающей средой ограничивался в опытах, главным образом, механизмом конвекции.

          В  таблице 2 представлены  результаты эксперимента (коэффициенты ослабления   g_k,  g_оп,  степень просветления  dt),  в  котором  мощное излучение фокусировалось в центр камеры. Параметры излучения в опыте были следущие:  P = 12  кВт,  w_вх =  1,2  кВт/см²,  w_вых =  2,2 кВт/см² (в отсутствие тумана ),  w_ц  = 10 кВт/см² ,  t_возд = 20 с. 

Как видно из табл. 2, за время  t  » 0,1с  образуется  канал  со степенью просветления     dt  » 85%, при этом скорость просветления достигает значения

V » 48 м/с. Масштаб нелинейного взаимодействия пучка с аэрозолем  в

процессе воздействия на туман в моменты времени t_возд = 0 ; 0,1; 1 с  составлял  соответственно L_a  =  1,1 ;  3,2 ;  46,5  м.

Анализ полученных результатов показывает, что при  воздействии на туман излучения с мощностью 12 - 16 кВт начиная с определенного момента времени t_Δγ существенно менялся  коэффициент ослабления излучения вне зоны воздействия. В табл. 2 даны величины средней скорости уменьшения коэффициентов ослабления V_Dg  для времени воздействия Δt = 5 с.

 

Табл. 2. Зависимость степени просветления тумана dt  от времени t  для

 t _0,63  = 9,9 и  P = 12 кВт.

tвозд, с	gопор, м-1	g кан, м-1	dt, %
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1 2 3 4 5	2,08 2,08 2,08 2,08 2,08 2,08 2,08 2,08 2,08 1,99 1,99 2,03 1,93 1,95	0,31 0,18 0,14 0,12 0,1 0,08 0,07 0,06 0,05 0,05 0,07 0,1 0,1 0,05	85 92 93 94 95 96 97 97 97 98 97 95 99 97

 

     Табл. 3. Влияние мощного ИК - излучения на  скорость изменения коэффициентов

ослабления на  l = 0,63 мкм  вне зоны воздействия.

aоп, м-1	P, кВт	D внеш, мм	tвозд, с	tDg, с	VΔγ·10-2, м-1/с
1,76 1,57 1,56 2 2 1,91 2,08 2,04	14,8 14,8 15,45 13,65 13 13,3 12 13,8	65 65 65 60 60 45 45 45	36 22 21 12 23 12 20 21	7 11 10 10 10 11 12 9	5,9 6,4 4,5 4,4 4,4 5,7 3,7 3,1

 

Отметим, что в экспериментах с другим  CO₂  - лазером (P = 1 кВт) при воздействии на туман излучения мощностью P = 150 Вт  V_Dg составила в среднем   0,003 - 0,006  м^-1 /с, что примерно в 10 раз меньше значений V_Dg, приведенных в табл. 2. Можно предположить, что при P = 12 - 16 кВт образуется  просветленная  область с диаметром больше, чем внешний диаметр  кольцевого пучка. В опытах коэффициент ослабления g_0,63 вне зоны воздействия, начинал уменьшатся в среднем через 10 с после начала воздействия. Поэтому скорость, с которой область повышенной прозрачности расширяется  в  горизонтальном направлении, составила  V_гк »3  см/с.  Указанное обстоятельство связано, очевидно, с тем, что некоторая часть тепла, выделяющегося в просветленной зоне, уходит через «боковые стенки». Причиной дополнительного теплоотвода является хаотическое движения среды в окрестности пучка. Величины скоростей V_k и V_гк характеризуют относительный вклад конвективного механизма переноса тепла по сравнению с кондуктивным и указывают на существенную роль турбулентной диффузии в формировании температурного поля при просветлении оптически плотных туманов и наличие горизонтальной составляющей скорости среды.

 

 

 

4. Естественный туман

 

    Экспериментальные исследования процесса просветления тумана  в натурных условиях мощным лазерным излучением проводились  весной   на трассе длиной 113 м с контролируемыми метеоусловиями по стандартной методике. Источником  когерентного излучения служил непрерывный CO₂  - лазер с  мощностью  1 кВт [12].  Опорное излучение на  l = 0,63 мкм распространялось  по трассе на расстоянии 21 см по горизонтали от  зондирующего  излучения. При этом излучение лазеров распространялось на высоте 3 - 4  м над поверхностью земли. 

    На рис.9 а, б приведен пример записи принимаемых  сигналов  на волне 0,63 мкм. В этом опыте мощное излучение,  прошедшее коллиматор, распространялось по трассе в виде сходящегося конуса. На передающем пункте диаметр пучка составил 90 мм, на приемном  -  40  мм, диаметр зондирующего пучка на l  = 0,63 мкм соответственно был 50  и 25 мм, диаметр опорного пучка - 20 и  30  мм.  Мощность  излучения, падающая на слой тумана, P = 550  Вт,  метеорологическая  дальность видимости в тумане S_m = 150 - 190 м. На рис.9 а виден эффект  просветления естественного тумана при открывании  затвора  и  воздействии излучения CO₂  - лазера на туман. Как известно, ветровое замывание обуславливает формирование стационарной зоны просветления, протяженность которой ограничена. При отсутствии поперечного ветра время установления стационарного просветления порядка времени  развития конвекции, в случае ветра ~ t_с  = 2a/V. Характерные максимумы сигнала объясняются влиянием  ветровых  потоков,  вносящих  холодные капли тумана в зону воздействия мощного излучения. Ветровой перенос капель тумана в направлении поперечном трассе распространения воздействующего пучка приводит к тому, что частицы среды находятся в зоне пучка ограниченное время. Время нахождения капель в области пучка при V ~ 1 м/с равно t = 2a/V ~ 0,1 с. При отсутствии ветра возникают конвективные потоки, которые также ограничивают время нахождения капель в зоне излучения. Формулу (11) для установившейся скорости конвективного всплывания среды в лазерном пучке представим в виде [27]:

            ,                                                

где b - коэффициент теплового расширения среды. Подставляя в последнюю формулу численные значения параметров  P = 550 Вт, g = 981 см² · с^-1, b = 3,3´10^-3 K^-1,  a = 5´10^-6 см^-1, найдем, что V_g = 1,3 см·с^-1. Таким образом, в присутствии ветра эффекты, вызываемые всплыванием тумана, не должны проявляться.

    В среднем интенсивность сигнала на  l = 0,63 мкм  возрастала на 13%. При скорости ветра 2-3 м/с степень просветления  составила  dt ≈ 4%. Предельную длину канала  просветления L_пр оценим, полагая, что ветер замоет канал за время а/V и скорость волны просветления равна  V_пр = w/gW_к (приближение Гликлера). В этом случае 

                                   L_пр » P /(pgW_к a V),                                               (20)

где g  - начальный коэффициент поглощения излучения на l = 10,6  мкм   в тумане, W_к  - характерная плотность  энергии, необходимая для испарения капель в тумане, a - радиус пучка, V  -  скорость ветра. Для условий эксперимента: g » 1,13´10^-2 м^-1, V = 3 м/с, а = 5 см , P =  550  Вт и W_к = 1,89 дж/см² получаем максимальную длину канала прозрачности L_пр = 4,8 м, что составляет 4,3% от длины трассы. 

В ряде  экспериментов  мощное  излучение  распространялось  по трассе расходящимся конусом, что достигалось  снятием  коллиматора. При этом диаметр пучка на l   = 10,6 мкм при входе в туман  составлял 50 мм, в конце трассы - 140 мм с более интенсивной центральной частью диаметром 40 мм. При мощности излучения P = 1 кВт метеорологической дальности видимости S_m  = 290 - 440 м, временных интервалах воздействия t_возд = 20 - 30 с, скорости бокового ветра V = 1,5-3 м/с  интенсивность сигнала на  l  = 0,63 мкм в канале возрастала в  среднем  на 9%, степень просветления составила  dt  ≈  3,4%. 

    При северо-восточном ветре,  который дул почти перпендикулярно направлению распространения мощного ИК-излучения, наблюдалось  возрастание опорного сигнала на  l  = 0,63 мкм вследствие  сноса  ветром просветленной области. В этом сеансе P = 0,9 кВт, V = 1 м/с,  S_m   = 800 - 1100 м. При этом интенсивность сигнала на l  = 0,63 мкм в  канале возрастала в среднем на 18%, степень просветления составила   dt ≈ 4%. 

 

 

5. Снег

 

     Измерение ослабления излучения с мощностью  ~1 кВт в снегопадах на трассе протяженностью 760 м  проводилось в марте - апреле месяце. Было проведено  40  опытов. При этом интенсивность выпадения снега I_сн   определялась  по количеству воды в единицу времени, образовавшейся в результате  его таяния на заданной площадке.  Измерения  интенсивности снега производились в одной точке трассы на приемном пункте весовым методом при помощи кювет, пробы снега брались  с  интервалами от 10 до 30 минут в зависимости  от интенсивности  снегопада. Наблюдения показали, что малые величины I_сн    характерны для снега в виде мелких кристаллов и снежинок,  а большие значения I_сн  -  для снега  с крупными снежинками и хлопьями.

     Ниже приведены усредненные коэффициенты ослабления  излучения CO₂ - лазера (передаваемая мощность P₁= 800 Вт) в зависимости от интенсивности снегопада при температуре воздуха T = 0 -  +1 ⁰C на трассе длиной 760 м: 

               

Iснега, мм/час	0,2	0,45	1,15	1,4	1,95
g, дБ/км	11,9	17,6	27,1	32,1	34,6

 

Каждая из приведенных величин   является результатом  усреднения по нескольким опытам, проведенным в течение 30 минут. 

      В работе [28] проводились измерения ослабления лазерного излучения на волне 10,6 мкм в снегопадах на трассе общей протяженностью 1360  м.  При этом в экспериментах применялся маломощный CO₂ - лазер (P = 3Вт), приемный и передающий пункт находились в одном месте, для  поворота излучения в конце трассы ( L =  680 м )  устанавливался уголковый  отражатель. Получены [28]  эмпирические зависимости  g_10,6   от интенсивности   снегопада в диапазоне 0,1 < I_сн < 2,5 мм/час; при этом максимальное ослабление составило около 30 дБ/км. Установлено, что снегопады могут вызывать более интенсивное ослабление излучения по сравнению  с дождем, так как при одинаковых интенсивностях выпадения водность в снегопаде превышает водность в дожде. Кроме того, при одинаковых массах частиц эффективное сечение ослабления снежинки превышает сечение капли дождя.

    Приведенные выше коэффициенты ослабления  g   на  7…10 дБ/км  больше соответствующих величин, полученных в работе [28], где  измерения проводились в сухом снеге. Например, в  опыте, когда снег падал в виде влажных хлопьев, передаваемая мощность была P₁  = 740 Вт, принимаемая – P₂ = 0,5 Вт, при этом коэффициент передачи  ( к = P₂ / P₁ ) составил к ~ 0,001 , а коэффициент ослабления -  g_10,6  » 42 дБ/км. 

    Представляло интерес определить погрешность измерений коэффициентов ослабления в снегопаде путем проведения соответствующих измерений  в свободной атмосфере. Измерения ослабления на волне 10,6 мкм проводились в марте – мае месяце.   Перехват ИК излучения   осуществлялся сферическими зеркалами на передающем и приемном пунктах. Излучение лазера фокусировалось  коллиматором, диаметр выходящего  из коллиматора пучка составлял 90 мм. 

Оценим  характерную длину нелинейного взаимодействия в атмосфере по формуле [22]:

        ,                                                                    (21)

Z₀  определяет расстояние , на котором изменения n в области  пучка приводят к его заметному искажению. Здесь p - атмосферное давление, V₀-скорость бокового ветра, g - отношение теплоемкостей среды при постоянном давлении и постоянном объеме, n₀ – коэффициент преломления воздуха. В частности, полагая  p = 1013,25 мбар (1атм);  n₀ – 1 = 2,67 × 10^-4; ( g - 1 ) = 0,4; и подставляя в (13)   параметры эксперимента P = 1кВт; a =  10^-4 м^-1; а = 5× 10^-2 м для трех значений скорости ветра V₀ = 1, 2, 3 м/с  найдем соответственно величину Z₀  = 2280, 3230, 3950 м.  Таким образом, на трассе протяженностью ~ 1 км и P » 1кВт пучок не должен искажаться вследствие изменения показателя преломления воздуха.

          Трасса протяженностью 113 м. Диаметр пучка на приемном пункте равнялся 40 мм. Мощность  излучения в начале и конце трассы измерялась с помощью  накопительных калориметров. Мощность P определялась  по  номограммам,  исходя  из измеренных величин экспозиции (времени воздействия) t  и  приросту температуры воды в калориметре  T: 

                                        ,                                         (22)

где C_S  - теплоемкость  калориметра и t  - постоянная   времени. Погрешность измерений составляла 4%. В табл. 4 приведены результаты  калориметрических  измерений для трех типичных опытов, выполненных при абсолютной влажности воздуха ( или парциальной  плотности водяного пара r_п ) а_вл  » 4 г/м³, температуре воздуха T = 0⁰ C и скорости ветра V=  2 - 4 м/с. При этом на приемном пункте мощность поочередно измерялась двумя калориметрами, для которых в  табл.  4  даны  соответствующие коэффициенты передачи.   

 

 

Табл. 4.  Потери энергии излучения CO₂ - лазера на трассе длиной 113 м.  

            

 

     Измеренные значения коэффициентов передачи k  показывают,  что потери энергии на короткой трассе практически отсутствуют.

     Трасса протяженностью 760 м. Мощность на передающем и приемном пунктах измеряли с помощью калориметрических измерителей мощности типа  М3-13/1. Погрешность измерений такого измерителя - 7%. При контрольных  измерениях показания двух приборов отличались не более, чем на 3%.

     На приемном пункте сечение центральной части пучка было эллипсом, вытянутым  по вертикальной оси (120 ´ 100 мм). Степень влияния наведенной конвекции на тепловую дефокусировку определяется вкладом механизмов теплопроводности и конвекции в охлаждение области пучка. Эта роль характеризуется числом Пекле [27]: Pe = aV₀ /(4a₁²). Нарушение осевой симметрии будет происходить, если Pe > 1, а условие возникновения наведенной конвекции в атмосфере имеет вид:( aа³P )^1/3 > 0,1. Для  данных экспериментов Pe >>1 и ( aа³P )^1/3 ~ 0,3. Следовательно, пространственное перераспределение интенсивности в поперечном сечении мощного пучка СО₂-лазера может быть обусловлено, конвекцией и дифракционной расходимостью. Соответствующие распределения интенсивности излучения по сечению  пучка  были получены в процессе измерений на приемном пункте помощью передвигаемого в горизонтальной плоскости  приемника  ИК-излучения. Характерные экспериментальные зависимости распределения интенсивности для двух опытов даны на рис.10. Здесь же приведена аппроксимация результатов измерений полиномом седьмой степени, найденная по методу наименьших квадратов. Можно видеть,  что при длине трассы 760 м  характерный размер пучка на приемном пункте ~ 60 см.

          Поглощение излучения СО₂- лазера в приземной атмосфере вызывается водяным паром и углекислым газом, а также  частицами аэрозоля. Анализ результатов измерений  мощностей  P₁   и  P₂ , выполненных при  а_вл    = 4,5 г/м ³, T = 0⁰C и V = 2 - 4 м/с   показал, что среднее значение коэффициента  передачи  k » 0,74.  В  отдельных опытах коэффициент передачи достигал величины k » 0,84. Семь серий  измерений на длинной трассе было выполнено непосредственно после снегопадов, когда ветер практически отсутствовал. При этом абсолютная влажность и  температуры воздуха были равны для них 4,4 г/м³  и +1⁰C  соответственно. Величина коэффициента передачи оказалась  несколько выше, чем при ветре и составила в среднем 0,77, коэффициент ослабления изменялся в пределах: g_10,6 = 0,7 - 0,77 дБ/км. Ниже приведены  коэффициенты ослабления излучения CO₂ -лазера на трассе длиной 760м  в зависимости от абсолютной влажности  воздуха  а_вл :

 

 

Каждая из приведенных величин   является результатом усреднения по 10 - 20 опытам. 

    Представленная здесь совокупность экспериментальных данных показывает, что коллимированный  мощный лазерный пучок на волне 10,6 мкм распространяется в свободной атмосфере практически без потерь  энергии на расстоянии порядка  километра. При этом просветление водного аэрозоля  с   оптической толщиной порядка 10 возможно  излучением CO₂- лазера с мощностью 12-16 кВт. Время образования канала ~ 0,035 с, скорость просветления неподвижного тумана составляет ~ 140 м / с, а КПД преобразования лучистой энергии в энергию испарения достигает ~ 34 %. Ветровой перенос капель тумана существенно влияет на динамику просветления в натурных условиях.  В случае снегопадов мощности просветляющего излучения должны быть увеличены по крайней мере на три порядка величины.

 

 

6. СПИСОК   ЛИТЕРАТУРЫ

 

1.  Воробьев В.В. Тепловое самовоздействие лазерного излучения в атмосфере.

     Теория и модельный эксперимент. М.: Наука, 1987. 200 с. 

2.  Волковицкий О.А., Седунов  Ю.С.,  Семенов  Л.П. Распространение       интенсивного лазерного излучения в  облаках.  Л.:  Гидромет., 1982. 312 с. 

3. Зуев В.Е., Землянов А.А., Копытин Ю.Д., Кузиковский А.В.  Мощное        лазерное излучение в атмосферном  аэрозоле. Новосибирск: Наука, 1984. 223 с.

4.  Гордин М.П., Грачев Ю.Н., Лоскутов В.С. и др. // Изв. АН СССР. Сер. Физ.    1985. Т. 49.  №  3. С. 450.

5.  Рудаш В.К. // Квантовая электроника. 1994. Т. 21. № 2. С. 137.

6.  Землянов А.А. // Оптика атмосферы и океана. 1995.  Т. 8. № 1-2. С. 89.

7.   Коровин В.Я. Труды ин-та эксп. Метеорологии. 1975. № 11 (54). С. 34.

8.   Рудаш В.К., Соколов А.В._; Стрелков Г.М. //Тезисы докл. I Всес. совещ. по атмосферной оптике.Томск: ИОА СО АН СССР, 1976. Ч. 2. С. 175.

9.  Зуев В.Е., Кузиковский А.В., Погодаев В.А.,  и др.// ДАН СССР. 1972. Т. 205. С.1069. 10.   Кузиковский А.В.// Изв. вузов. Сер. Физика. 1970. Т.13. № 5. С.89.

11.   Кузиковский А.В., Погодаев В.А., Хмелевцов С.С.// Инж-физ.ж. 1971.Т. 20. № 1. С.21. (1971).

12.   Колосов М.А., Рудаш В.К., Соколов А.В., Стрелков Г.М. //  РЭ. 1974. Т. 19. № 1. С. 45.

13.Алмаев Р.Х., Волковицкий О.А., Семенов Л.П., Слесарев А.Г. //Метеорология и гидрология. 1995.  № 4. С. 22.

14.    Гордин М.П., Стрелков Г.М. //Тезисы докл. I Всес. совещ. по атмосферной оптике. Томск: ИОА СО АН СССР, 1976. Ч. 2. С. 153.

15.    Гордин М.П., Стрелков Г.М.// Тезисы докл. IV Всес. симп. по распространению лазерного излучения в атмосфере. Томск: ИОА СО АН СССР, 1977. С. 46.

16. Рудаш В.К., Стрелков Г.М. //Тезисы докл. II Всес. симп. по распространению лазерного излучения в атмосфере. Томск: ИОА СО АН СССР, 1973. С. 303.

17. Рудаш В.К., Стрелков Г.М.// Препринт. М: ИРЭ АН СССР, 1973.  №132. С. 20.

18. Рудаш В.К., Бисярин В.П., Ильин Н.М.,  и др.// Квантовая электроника, № 5(17), 21 (1973).

19.Беленький  А.М., Зуев Г. М., Косырев Ф.К. и др. // Сварочное производство.     1977.  № 11. С.  23.

20. Погодаев В.А.,Рождественский А.Е., Чистякова Л.К.// Изв. вузов. Сер. Физика, 1980 .Т.23.№3.С.34.

21.  Бисярин В.П., Ильин Н.М., Рудаш В.К. и др. //  Тез. докл. 1Х Всесоюзной   конференции по распространению радиоволн.  Харьков: ИРЭ АН УССР, 1969. Ч. 2. С. 180.

22.  Wallace J., Camac M. //  Journ. Opt. Soc. Am. 1970. V. 60.  №  2. P.1587.

23.  Арманд С.А., Бехтин Ю.И., Пожидаев В.Н. // РЭ. 1976. Т. 21. №  10. С. 2033.

24.Glickler S.L. // Appl. Optics. 1971. V. 10.  №  3.  P. 644.

25.Колосов М.А., Пожидаев В.Н., Соколов А.В., Стрелков Г.М. // Проблемы   современной радиотехники и электроники . Под ред. Котельникова В.А.  М.:  Наука, 1980.  С.181.

26.Бисярин В.П., Ефременко В.В., Колосов М.А и др. //  Изв. Вузов. Физика. 1983.Т. 26. № 2. С. 23.

27.Livingston P.M. // Appl. Optics. 1971. V. 10.  № 2.  P. 426.

28.  Бисярин В.П., Бисярина И.П., Рудаш В.К., Соколов А.В. // РЭ. 1971. Т. 16. № 10.  С. 1765. 

 

 

 

7.  рисункИ

 

---

 

Рис.1

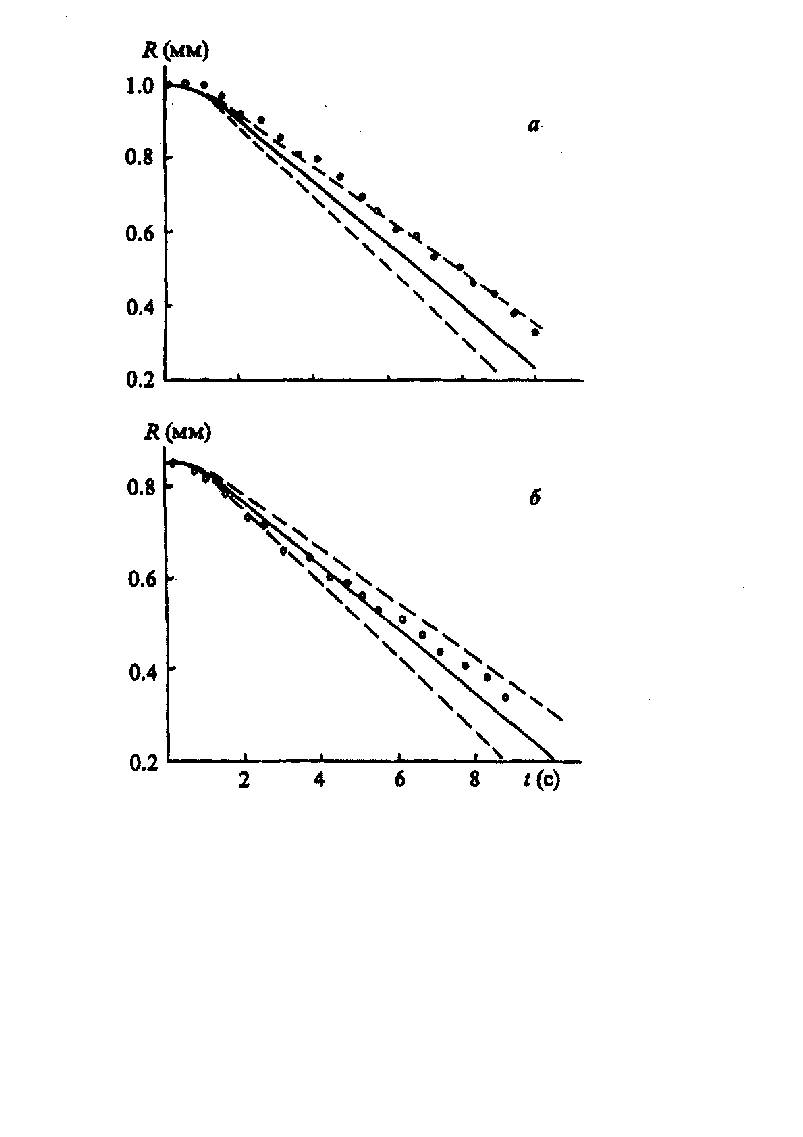
Рис.1. Сравнение экспериментальных (точки) и теоретических (кривые) зависимостей радиуса конвективно испаряющейся капли при  R₀ = 1 (а) и 0,85 мм (б),   w= 76 (а) и 65 Вт/см² (б) (сплошная кривая) и (1 ± 0,15)×76 (а) и (1 ± 0,15)×65 Вт/см² (б) (пунктир).

---

 

Рис.2.

Рис.2. Испарение капли в конвективном режиме с выбросами пара: точки - измерения при  w = 76 (1), 480 (2) и 1650 Вт/см² (3), кривые - расчет по формуле (3).  

---

 

Рис.3.

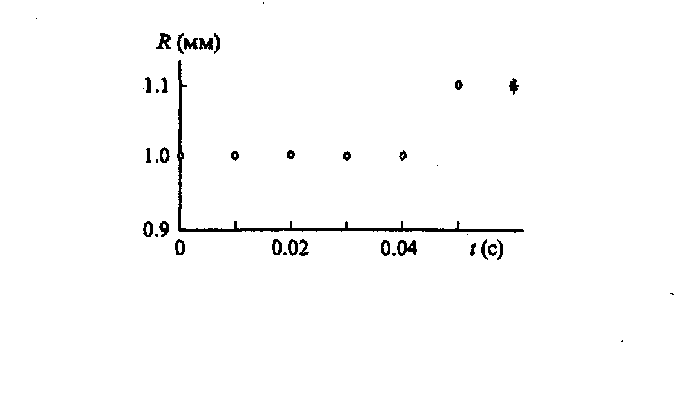
Рис.3. Испарение капли во взрывном режиме при w = 1,1 × 10⁴ Вт/см² (звездочка - взрыв).

---

 

Рис.4.

Рис.4. Взрыв водяной капли при w = 10⁴ Вт/см² и диаметре пучка (d = 10 мм: капля, образовавшаяся после взрыва подвешенной на ни­ти капли (t_взр = 0,056 с) (а) и взрыв свободной капли через (t = 0,008 с после ее отрыва от нити (6).

---

 

Рис.5.

Рис.5. Изменение радиуса ледяной сферической частицы (о) и водяной капли (•) в поле излучения с w= 30 Вт/см² ( R₀ = 1 мм), а также теоретический расчет для водяной капли при w = 25,5 (1), 30 (2) и 34,5 Вт/см² (3).

---

 

Рис.6.

Рис.6. Схема измерений: 1 - затвор для перекрытия излучения СO₂ - лазера,  2 - зеркало измерителя  мощности,  3, 4, 5 -  поворотные зеркала, 6 - He-Ne - лазер, 7 - модулятор излучения, 8 - коллиматор, 9 - He-Ne - лазер, 10 - модулятор излучения, 11 - камера ИТ, 12 - диафрагма, 13 - зеркало с отверстием, 14 - кварцевая пластина, 15 - фотодиод, 16 - поглотитель  излучения - 10,6  мкм,  17-18  - зеркала, 19 - фотоэлектронный умножитель, 20 -21-  усилители, 22 - детектор, 23  -самописец.

---

 

Рис.7а, б.

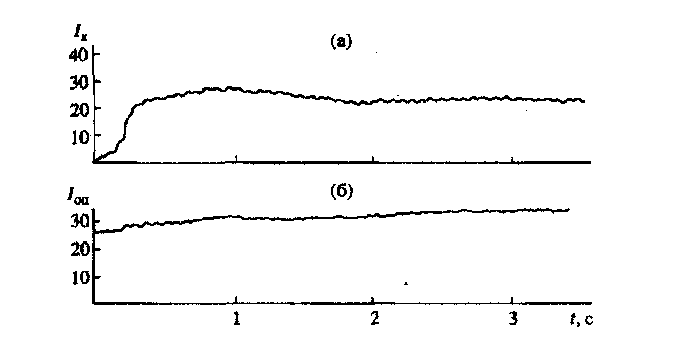
Рис.7а, б. Просветление искусственного тумана: излучение на l =  0,63 мкм в канале просветления (а) (шкала усилителя – 1в) и вне канала (б) (шкала усилителя – 3мв).

---

 

Рис.8 а, б.

Рис.8 а, б. Замывания канала просветления:  излучение на l =  0,63 мкм в канале (а) (шкала усилителя – 1в), и вне канала (б)(шкала усилителя – 3мв).

---

 

Рис.9 а, б.

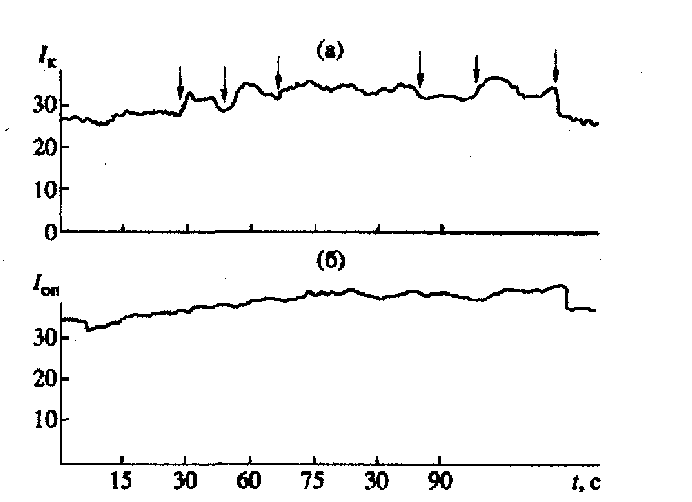
Рис.9 а, б. Просветление  естественного  тумана:  излучение на l = 0,63 мкм в канале (а) (стрелками  отмечены  моменты воздействия излучения СО₂ - лазера) и вне канала (б).

---

 

Рис.10.

Рис.10. Распределения интенсивности излучения  мощного  пучка на приемном пункте при L = 760м (точки -  эксперимент; сплошная кривая -   аппроксимация).

---

 

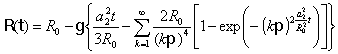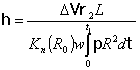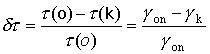
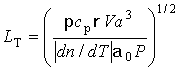
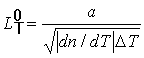
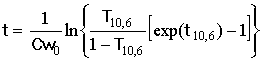
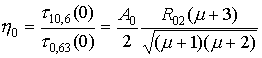
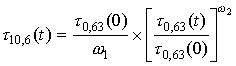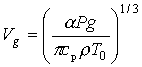
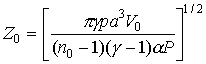
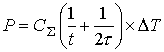оглавление

дискуссия