|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 2, 2003 |
|
Анализ FPGA, реализующих нелинейные цифровые фильтры
Погорелов А. М., pogorelov@mail.nnov.ru
Нижний Новгород, НИИИС, инж.-иссл.
Получена 3 февраля 2003 г.
В данной статье рассмотрен анализ нелинейных цифровых фильтров реализованных на базе FPGA (Field Programmable Gate Array). Представленные таблицы получены экспериментальным путём, на основе которых были построены зависимости максимальной частоты фильтра от количества вентилей на кристалле. Фильтры отличаются количеством и разрядностью функций.
Одной из наиболее эффективных реализаций, нелинейных цифровых фильтров является использование FPGA(Field Programmable Gate Array).
В настоящей работе рассматривается зависимость быстродействия КИХ фильтра урысоновского типа (рисунок1) с нелинейностями в отводах, на FPGA от параметров фильтра и параметров типов кристалла. Ниже приведено уравнение КИХ фильтра урысоновского типа:
где {ai}-постоянные коэффициенты, а fi(x)-функции, определённые на R и принимающие значения из R.
Ввиду того, что быстродействие устройств реализуемых на FPGA зависит от многих факторов, нами была выбрана методика, заключающаяся в реализации проектов с помощью Foundation Series 4.2.i, максимально учитывающая характеристики кристаллов, в том числе и особенности топологического устройства с помощью принятых инструментов. Для анализа использовалось семейство FPGA(Virtex). Основным инструментом проектирования был пакет фирмы Xilinx - Foundation Series 4.2.i.
Основными этапами проектирования являлись:
1. Создание проекта в виде схемы;
2. Написание user constrains file(файл констант пользователя);
3. Моделирование, с этим user constrains file, созданного проекта в кристаллах от 50000 до 300000 вентилей, на разных скоростях(Speed4,5,6);
4. Создание нового user constrains file и повторение всей выше описанной процедуры.
Были написаны 5 user constrains files, которые и определили использование аппарата математической статистики. Проводился анализ нескольких фильтров урысоновского типа, имеющих 4 и 8 базисных функций, т.е. 3 и 7 линий задержки (z-1, рис.1).
Рисунок 1
Функции табличные, управление извне. Одним из параметров определяющих сложность фильтра является разрядность фильтра.
Нами были проанализированы фильтры восьми и двенадцати разрядной архитектуры. Другими словами каждая из восьми или каждая из четырёх функций имеет 8 и 12 разрядов. То есть были рассмотрены варианты:
1.фильтр четвёртого порядка и каждая функция по 8 разрядов;
2.фильтр четвёртого порядка и каждая функция по 12 разрядов;
3.фильтр восьмого порядка и каждая функция по 8 разрядов;
4.фильтр восьмого порядка и каждая функция по 12 разрядов.
Был проведен анализ зависимости максимальной частоты работы фильтра, от числа вентилей на кристалле. При создании нескольких проектов одного и того же фильтра, на одном и том же кристалле, были использованы разные user constrains files[2]. User constrains files – файл констант пользователя, эти константы определяются при программировании. В число этих констант входят фиксированные задержки от используемого вывода на корпусе до используемого конфигурируемого логического блока, имеется возможность менять зарезервированные выводы для программирования и желаемая максимальная частота работы фильтра.
Было обнаружено, что максимальная частота меняется при использовании разных user constrains files. Использование аппарата математической статистики, позволило определить нам математическое ожидание величин максимальной частоты фильтра и среднее квадратичное отклонение частоты. В таблице 3 это величины m и q столбцы 7 и 8 соответственно. В таблице 3 в первом столбце указан номер эксперимента. В столбцах со второго по шестой - это полученные частоты в результате моделирования различных user constrains files. Значение частоты в даны МГц. В последнем столбце указан использовавшийся тип кристалла. Например, запись 50-4 означает, что был использован кристалл ёмкостью 50.000 вентилей со скоростью Speed-4.
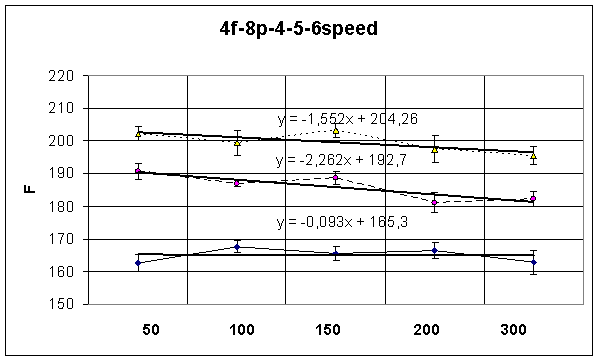
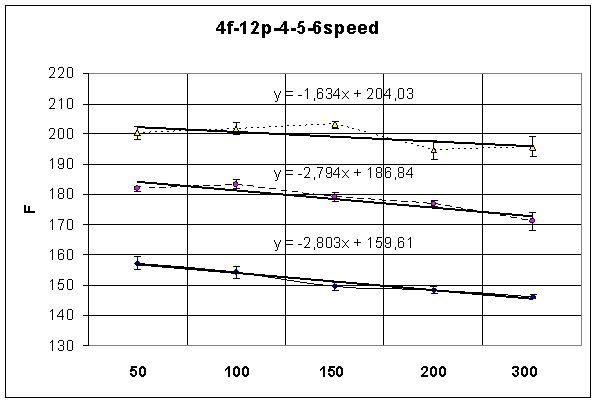
После построения графиков (рис. 2, 3, 4, 5) нам необходимо отметить, что с ростом числа вентилей, т.е. объёма кристалла, придётся поплатиться максимальной частотой работы фильтра. Это первое, что было обнаружено.
Второе - это увеличение среднего квадратичного отклонения (СКО) с ростом сложности фильтра. Рассмотрим это на примере выборки с показателем скорости Speed-5.
|
2,32 |
3,26 |
|
1,07 |
4,26 |
|
2,13 |
5,1 |
|
3,1 |
3,25 |
|
2,37 |
5 |
В таблице 1, в левой колонке приведены значения СКО для фильтра с 4 функциями, а правой СКО для фильтра с 8 функциями.
При увеличении числа табличных функций, а значит и при увеличении порядка цифрового фильтра, интервал доверительной вероятности растёт. Другим результатом является также установление факта, что с ростом разрядности входных функций интервал доверительной вероятности падает.
|
2,6 |
2,35 |
|
3,26 |
1,8 |
|
3,45 |
1,21 |
|
3,18 |
1,52 |
|
4,26 |
2,69 |
|
2,93 |
2,11 |
|
4,34 |
2,1 |
|
5,1 |
1,27 |
|
5 |
4,3 |
|
2,34 |
4 |
|
3,25 |
1,4 |
|
4,6 |
3,7 |
|
4,1 |
2,34 |
|
5 |
3,61 |
|
6,7 |
2,74 |
В таблице 2 представлены СКО фильтра восьмого порядка. В левой паре колонок представлены значения для Speed-4, в центральной паре для Speed-5, а в правой паре для Speed-6.
Третье, что было выявлено, рост числа функций обуславливает в свою очередь рост коэффициента падения максимальной частоты.
Y = -3,076X + 199,04 – зависимость для фильтра 8-го порядка, с 8-ми разрядными входными функциями с показателем Speed-4(рис.1).
Y = -1,552X + 204,26 – зависимость для фильтра 4-го порядка, с 8-ми разрядными входными функциями с показателем Speed-4(рис.2). В уравнениях Y-значение максимальной частоты фильтра, а X принимает значения от 1 до 5. Этим значениям соответствуют Х1-50000 вентилей, Х2-100000 вентилей, Х3-150000 вентилей, Х4-200000 вентилей, Х5-300000 вентилей.
Четвёртое – применение более скоростных кристаллов позволяет повысить максимальную частоту работы цифрового фильтра (рисунки 2,3,4,5). На этих рисунках верхние графики соответствуют Speed-6, средние Speed-5, а нижние Speed-4.
В среднем, при переходе от четырёхскоростного кристалла к пятискоростному, частота повышается на 15,76%, при переходе от пятискоростного кристалла к шестискоростному, частота фильтра повышается на 7,43%. В среднем, при переходе от четырёхскоростного кристалла к шестискоростному частота повышается на 24,4%.
Пятое – фильтр, у которого восемь 8-ми разрядных функций имеет следующую разницу, между среднеарифметическим значением математического ожидания частоты и величиной математического ожидания частоты в кристаллах с объёмами 50.000 вентилей - 3,8%; 100.000 – 1,3%; 150.000 – 0,8%; 200.000 – 1,3%; 300.000 – 3%(эти величины получены для кристалла Speed-4). Фильтр, у которого четыре 8-ми разрядных функций имеет следующие значения отклонения математического ожидания частоты фильтра, от среднеарифметического значения математического ожидания частоты 50.000 – 1,4%; 100.000 – 1,6%; 150.000 – 0,4%; 200.000 – 0,8%; 300.000 вентилей – 1,3%(эти величины получены для кристалла Speed-4).
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4f-8p |
|
m |
q |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
165,5 |
170,18 |
162,05 |
154,04 |
161,42 |
162,64 |
2,65 |
50-4 |
|
2 |
190,44 |
195,85 |
195,85 |
185,22 |
185,74 |
190,62 |
2,32 |
50-5 |
|
3 |
195,5 |
205,68 |
208,95 |
200,8 |
200,44 |
202,27 |
2,32 |
50-6 |
|
|
|
|
|
|
|
|
|
|
|
4 |
165,9 |
170,18 |
160,98 |
170,18 |
170,18 |
167,48 |
1,84 |
100-4 |
|
5 |
190,98 |
184,54 |
186,45 |
186,45 |
186,43 |
186,9 |
1,07 |
100-5 |
|
6 |
192,9 |
190,22 |
207,9 |
208,94 |
197,55 |
199,5 |
3,83 |
100-6 |
|
|
|
|
|
|
|
|
|
|
|
7 |
165,9 |
160,98 |
160,98 |
170,18 |
170,18 |
165,64 |
2,06 |
150-4 |
|
8 |
190,98 |
185,22 |
186,45 |
195,85 |
184,54 |
188,61 |
2,13 |
150-5 |
|
9 |
196,31 |
206,7 |
207,9 |
200,5 |
204,7 |
203,22 |
2,14 |
150-6 |
|
|
|
|
|
|
|
|
|
|
|
10 |
160,23 |
170,18 |
160,98 |
170,18 |
170,18 |
166,35 |
2,35 |
200-4 |
|
11 |
188,32 |
180,73 |
170,07 |
181,5 |
185,22 |
181,17 |
3,1 |
200-5 |
|
12 |
214,04 |
193,42 |
190,55 |
194,9 |
194,9 |
197,56 |
4,2 |
200-6 |
|
|
|
|
|
|
|
|
|
|
|
13 |
155,62 |
162,05 |
162,05 |
170,18 |
170,18 |
162,82 |
3,61 |
300-4 |
|
14 |
186,29 |
185,23 |
173,52 |
185,22 |
180,8 |
182,21 |
2,37 |
300-5 |
|
15 |
201,21 |
201,25 |
185,98 |
194,63 |
194,33 |
195,48 |
2,81 |
300-6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4f-12p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
162,47 |
160,18 |
155,11 |
158,6 |
150,42 |
157,37 |
2,11 |
50-4 |
|
17 |
183,12 |
182,58 |
182,58 |
182,58 |
178,54 |
181,88 |
0,84 |
50-5 |
|
18 |
193,35 |
204,7 |
198,18 |
204,7 |
201,17 |
200,42 |
2,14 |
50-6 |
|
|
|
|
|
|
|
|
|
|
|
19 |
158,58 |
155,93 |
155,93 |
154,82 |
146,41 |
154,33 |
2,08 |
100-4 |
|
20 |
186,95 |
182,58 |
184,37 |
178,22 |
184,37 |
183,3 |
1,45 |
100-5 |
|
21 |
194,55 |
204,7 |
204,7 |
199,76 |
204,7 |
201,68 |
2,02 |
100-6 |
|
|
|
|
|
|
|
|
|
|
|
22 |
149,86 |
150,6 |
150,6 |
152,23 |
144,6 |
149,58 |
1,3 |
150-4 |
|
23 |
178,03 |
181,88 |
178,54 |
178,22 |
178,54 |
179,04 |
1,57 |
150-5 |
|
24 |
199,56 |
204,7 |
204,7 |
204,7 |
201,78 |
203,09 |
1,05 |
150-6 |
|
|
|
|
|
|
|
|
|
|
|
25 |
148,35 |
150,74 |
145,71 |
151,15 |
146,16 |
148,42 |
1,12 |
200-4 |
|
26 |
178,03 |
180 |
173,55 |
178,22 |
175,22 |
177 |
1,02 |
200-5 |
|
27 |
182,88 |
200,12 |
196,16 |
199,76 |
194,48 |
194,68 |
3,14 |
200-6 |
|
|
|
|
|
|
|
|
|
|
|
28 |
145,71 |
144,89 |
144,89 |
149,3 |
146,78 |
146,31 |
0,82 |
300-4 |
|
29 |
163,19 |
174,99 |
168,41 |
180 |
168,69 |
171,06 |
2,9 |
300-5 |
|
30 |
187,41 |
196,16 |
188,89 |
204,7 |
201,61 |
195,75 |
3,4 |
300-6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8f-8p |
|
|
|
|
|
|
|
|
|
|
|
m |
q |
|
|
31 |
150,92 |
144,78 |
156,96 |
156,81 |
158,98 |
153,69 |
2,6 |
50-4 |
|
32 |
170,59 |
170,01 |
186,01 |
183,12 |
180 |
177,95 |
3,26 |
50-5 |
|
33 |
189,07 |
186,71 |
200,76 |
204,75 |
198,02 |
195,86 |
3,45 |
50-6 |
|
|
|
|
|
|
|
|
|
|
|
34 |
142,07 |
146,14 |
156,96 |
152,81 |
151,38 |
149,87 |
3,18 |
100-4 |
|
35 |
163,32 |
168,41 |
184,33 |
183,12 |
181,19 |
176,07 |
4,26 |
100-5 |
|
36 |
184,43 |
189,22 |
199,92 |
198,97 |
193,24 |
193,16 |
2,93 |
100-6 |
|
|
|
|
|
|
|
|
|
|
|
37 |
132,63 |
141,32 |
152,49 |
156,45 |
151,39 |
146,85 |
4,34 |
150-4 |
|
38 |
156,86 |
160,54 |
178,98 |
180,05 |
178,89 |
171,06 |
5,1 |
150-5 |
|
39 |
174,86 |
183,52 |
199,48 |
200,52 |
195,5 |
190,78 |
5 |
150-6 |
|
|
|
|
|
|
|
|
|
|
|
40 |
138,4 |
143,31 |
148,32 |
149,23 |
151,38 |
146,13 |
2,34 |
200-4 |
|
41 |
160,9 |
156,64 |
173,13 |
171,62 |
170,01 |
166,46 |
3,25 |
200-5 |
|
42 |
169,35 |
178,35 |
194,1 |
190,51 |
189,8 |
184,42 |
4,6 |
200-6 |
|
|
|
|
|
|
|
|
|
|
|
43 |
129,3 |
139,96 |
152,81 |
148,32 |
147,15 |
143,51 |
4,1 |
300-4 |
|
44 |
149,01 |
157,28 |
174,4 |
168,55 |
174,06 |
164,66 |
5 |
300-5 |
|
45 |
161,45 |
178,35 |
196,12 |
194,25 |
194,1 |
184,85 |
6,7 |
300-6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8f-12p |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
46 |
147,89 |
147,88 |
140,87 |
139,28 |
137,21 |
142,63 |
2,35 |
50-4 |
|
47 |
162,58 |
167,67 |
158,03 |
157,93 |
160,21 |
161,28 |
1,8 |
50-5 |
|
48 |
169,55 |
175,44 |
169,52 |
172,86 |
174,25 |
172,32 |
1,21 |
50-6 |
|
|
|
|
|
|
|
|
|
|
|
49 |
145,12 |
144,45 |
137,55 |
137,87 |
137,42 |
140,48 |
1,52 |
100-4 |
|
50 |
156,74 |
166,25 |
154,49 |
159,31 |
150,08 |
157,37 |
2,69 |
100-5 |
|
51 |
169,32 |
174,9 |
163,03 |
165,48 |
164,8 |
167,5 |
2,11 |
100-6 |
|
|
|
|
|
|
|
|
|
|
|
52 |
141,22 |
146,11 |
134,31 |
138,4 |
136,04 |
139,22 |
2,1 |
150-4 |
|
53 |
158,73 |
154,9 |
154,49 |
155,72 |
150,83 |
154,93 |
1,27 |
150-5 |
|
54 |
167,48 |
168,35 |
156,15 |
159 |
160,6 |
162,32 |
4,3 |
150-6 |
|
|
|
|
|
|
|
|
|
|
|
55 |
137,97 |
143,68 |
125,71 |
121,4 |
132,71 |
132,3 |
4 |
200-4 |
|
56 |
157,31 |
158,25 |
154,49 |
151,47 |
152,02 |
154,71 |
1,4 |
200-5 |
|
57 |
169,72 |
168,07 |
149,8 |
156,7 |
158,48 |
160,6 |
3,7 |
200-6 |
|
|
|
|
|
|
|
|
|
|
|
58 |
135,94 |
135,8 |
130,12 |
130,17 |
123,26 |
131,06 |
2,34 |
300-4 |
|
59 |
156,5 |
156,74 |
142,61 |
143,23 |
139,55 |
147,23 |
3,61 |
300-5 |
|
60 |
167,48 |
163,45 |
161,6 |
168,18 |
152,91 |
162,72 |
2,74 |
300-6 |
Рисунок 2
Рисунок 3
Рисунок 4
Рисунок 5
Литература.
- Крылов В. В., Херманис Э. Х. Модели систем обработки сигналов. Рига.: Зинатне, 1981, 212 с.
- Xilinx Inc. The Programmable Logic Data Book. 2000.
Xilinx Inc. XCELL. The Quaterly Journal For Xilinx Programmable Logic Users.