|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 2, 2004 |
|
ВОЗБУЖДЕНИЕ ПЛАНАРНОЙ РЕШЕТКИ ЩЕЛЕВЫХ ИЗЛУЧАТЕЛЕЙ
ВОЗБУДИТЕЛЕМ КОНЕЧНЫХ РАЗМЕРОВ
М.Д. Дупленкова
Московкий энергетический институт
Получена 16.02.2004 г.
Аннотация
Рассмотрена задача о возбуждении двумерным пучком Т-волн плоского волновода решетки щелевых излучателей, выполненных в экране плоского волновода. Пучок Т-волн моделирует поле, порождаемое возбудителем решетки конечных размеров. Решение задачи основано на полученном ранее решении задачи о возбуждении решетки одиночной Т-волной. Волновой пучок представляется в виде спектра Т-волн с разными волновыми векторами. Рассеянное поле в силу принципа суперпозиции также представляется в виде аналогичного спектрального разложения. Приводятся результаты численного исследования решеток, возбуждаемых пучками. Полученные результаты позволяют оценить влияние конечных размеров возбудителя на параметры решетки: диаграмму направленности, коэффициент усиления и т.д.
Введение
Работа посвящена методам анализа антенных решеток щелевых излучателей на основе плоского металлического волновода и является продолжением серии работ [1,2,3], посвященных антеннам данного типа. В работах [1,2] исследована бесконечная двумерно-периодическая решетка щелей. В работе [3] получено электродинамическое решение задачи о возбуждении решетки конечной длины, возбуждаемой собственной волной плоского волновода (ПВ), падающей под произвольным углом.
В работах [1,2,3] мы рассматривали решетку щелей, бесконечную вдоль оси 0y и считали, что решетка возбуждается основной Т-волной ПВ. То есть в качестве возбудителя рассматривалась волна с плоским фронтом. Однако реальный возбудитель имеет конечные размеры, а распределение возбуждающего поля может оказаться неравномерным. В данной работе мы продолжаем исследование антенных решеток такого типа, причем в первую очередь нас интересует влияние указанных выше факторов. Особенность возбудителя, имеющего конечные размеры заключается в том, что он порождает не одну плоскую волну, а целый спектр плоских волн, то есть волновой пучок. Этот волновой пучок затем распространяется в плоскости ПВ и возбуждает собственно решетку. Таким образом, единая задача о возбуждении решетки возбудителем конечных размеров разделяется на две более простые подзадачи. Первая из них – это задача о возбуждении волнового пучка, а вторая – это возбуждение решетки этим волновым пучком. Будем последовательно решить данные задачи.
1. Возбуждение волнового пучка
Рассмотрим излучение возбудителя, находящегося в ПВ, причем предполагаем, что ПВ одномодовый и в нем может распространяться только основная Т-волна. Отсюда, в частности, следует, что говоря о пучке в ПВ мы имеем ввиду двумерный волновой пучок, образованный спектром Т-волн.
Отметим, что конкретная конструкция возбудителя нас в данный момент не интересует. Вообще говоря, возбудитель представляет собой антенну, предназначенную для излучения не в свободное пространство, а в ПВ. Роль такой антенны может выполнять плоская рупорно-линзовая антенна, плоская рупорно-зеркальная антенна или многоканальный делитель мощности. Общим свойством всех перечисленных устройств является то, что они создают в некотором сечении ПВ амплитудно-фазовое распределение поля, имеющее постоянную фазу и медленно меняющуюся амплитуду. Поле, сформированное возбудителем, возбуждает ПВ. Для задачи возбуждения решетки существенным является только вид амплитудно-фазового распределения поля в раскрыве возбудителя. При этом способ его формирования значения не имеет. Поэтому далее будем рассматривать возбудитель как некоторое сечение ПВ, в котором существует заданное поле, являющееся первичным по отношению к ПВ и решетке и будем решать задачу возбуждения ПВ и решетки этим первичным полем.
Воспользуемся теоремой
эквивалентных поверхностных электрических и магнитных токов [4]. Обозначим
векторы электромагнитного поля порожденного возбудителем через ![]() и
и ![]() . Разделим все пространство
замкнутой поверхностью S,
охватывающей возбудитель, на две области 1 и 2 (рис. 1).
. Разделим все пространство
замкнутой поверхностью S,
охватывающей возбудитель, на две области 1 и 2 (рис. 1).
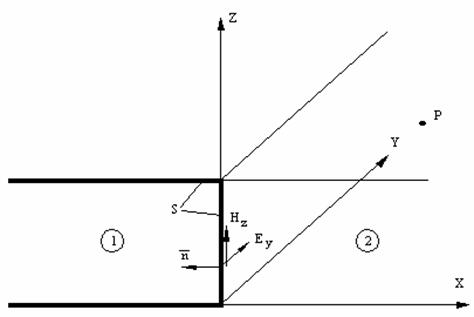
Рис. 1
Известно, что основная
Т-волна ПВ имеет три компоненты электромагнитного поля: ![]() . Касательными к поверхности S являются компоненты
. Касательными к поверхности S являются компоненты ![]() и
и ![]() .
.
Пользуясь линейностью уравнений Максвелла, рассмотрим мысленно по отдельности:
1) компоненту вектора НВу , полагая ЕВz=0;
2) компоненту вектора ЕВz , полагая НВу=0.
В первом случае поверхность S представляется идеальным электрическим проводником, поскольку на ней вектор магнитного поля имеет только тангенциальную составляющую. По теореме эквивалентности по поверхности S течет поверхностный электрический ток, плотность которого определяется выражением
![]() , (1)
, (1)
где ![]() - тангенциальная к поверхности S компонента магнитного поля
возбудителя,
- тангенциальная к поверхности S компонента магнитного поля
возбудителя, ![]() -
нормаль к поверхности, внешняя относительно рассматриваемой области (область 2
см. рис.1).
-
нормаль к поверхности, внешняя относительно рассматриваемой области (область 2
см. рис.1).
Покажем, что для решения задачи о возбуждении решетки на основе ПВ можно воспользоваться двумерной функцией Грина. Рассмотрим возбуждение ПВ электрическим током
![]() . (2)
. (2)
Так как ПВ является
структурой, ограниченной вдоль оси 0z, то задачу его возбуждения удобно решать методом собственных функций.
Собственные функции для ПВ хорошо известны [4]: ![]() , это система взаимно ортогональных
собственных функций. В силу ортогональности собственных функций
, это система взаимно ортогональных
собственных функций. В силу ортогональности собственных функций ![]() , постоянный по оси 0z
ток
, постоянный по оси 0z
ток ![]() порождает
лишь собственную волну с n=0,
то есть
порождает
лишь собственную волну с n=0,
то есть ![]() и
и ![]() . Таким образом данная
задача сводится к двумерной.
. Таким образом данная
задача сводится к двумерной.
Векторный потенциал эквивалентного поверхностного электрического тока в некоторой точке Р области 2 может быть определен по формуле:
![]() ,
,
где в силу двумерности задачи
 ,
,
![]() - волновое число свободного
пространства, e -
диэлектрическая проницаемость пластины, а электрический ток определяется выражением (2).
- волновое число свободного
пространства, e -
диэлектрическая проницаемость пластины, а электрический ток определяется выражением (2).
Введем следующее обозначение
![]() . (3)
. (3)
Тогда получаем для векторного потенциала новое представление:
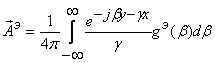 , (4)
, (4)
где ![]() .
.
Тогда при ![]() величина g является действительной и экспонента
под интегралом в (4) описывает затухающие волны, амплитуда которых уменьшается
по экспоненте при удалении в обе стороны от оси 0y. Если же
величина g является действительной и экспонента
под интегралом в (4) описывает затухающие волны, амплитуда которых уменьшается
по экспоненте при удалении в обе стороны от оси 0y. Если же ![]() , то получаем бегущие волны,
распространяющиеся в обе стороны в направлении оси 0x.
, то получаем бегущие волны,
распространяющиеся в обе стороны в направлении оси 0x.
Напряженности электрического и магнитного полей могут быть определены через векторный потенциал по формулам [4]:
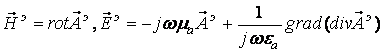 .
.
Тогда в нашем случае компоненты поля выражаются следующими соотношениями:
 . (5)
. (5)
Во втором случае поверхность S представляется идеальным магнитным проводником, поскольку вектор электрического поля имеет только тангенциальную составляющую. На поверхности S во втором случае течет поверхностный магнитный ток, плотность которого численно равна тангенциальной составляющей напряженности электрического поля и определяется по формуле:
![]() , (6)
, (6)
где ![]() - тангенциальная к поверхности S компонента электрического поля
возбудителя. Векторный потенциал эквивалентного поверхностного
магнитного тока определяется по формуле:
- тангенциальная к поверхности S компонента электрического поля
возбудителя. Векторный потенциал эквивалентного поверхностного
магнитного тока определяется по формуле:
 , (7)
, (7)
где ![]() , (8)
, (8)
если ![]() , (9)
, (9)
а электромагнитные поля определяются по формулам [4]:
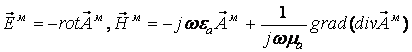 .
.
Тогда в нашем случае компоненты поля выражаются следующими соотношениями:
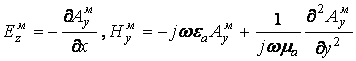 (10)
(10)
Таким образом, компоненты поля в точке наблюдения Р определяются суммой:
![]() (11)
(11)
Раскрывая векторные произведения (1) и (6), выражаем эквивалентные токи через поле возбудителя:
![]() . (12)
. (12)
Воспользуемся теперь тем обстоятельством, что возбудитель порождает волновой пучок:
![]() ,
,
где ![]() - проекция волнового вектора
пучка на ось 0х.
- проекция волнового вектора
пучка на ось 0х.
Назовем функцию ![]() возбуждающей функцией.
возбуждающей функцией.
Если размер возбудителя ![]() много больше длины
волны
много больше длины
волны ![]() , то
соотношения между компонентами электромагнитного поля приближенно будут такими
же, как для однородной плоской волны:
, то
соотношения между компонентами электромагнитного поля приближенно будут такими
же, как для однородной плоской волны:  , (13)
, (13)
где b0 – проекция волнового вектора пучка на ось 0у.
Тогда в силу (12) распределение возбуждающих токов (2) и (9) будут связаны соотношением:
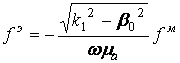 . (14)
. (14)
Переходя от векторных
потенциалов (4), (7) к компонентам поля в соответствии с (5) и (10), получаем:![]()
 (15)
(15)
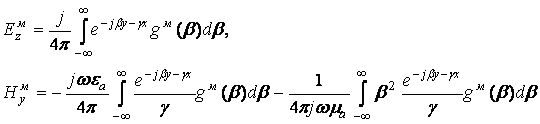 (16)
(16)
Тогда суммарное поле согласно (11) определяется следующими выражениями:
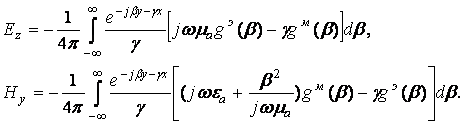 (17)
(17)
Рассмотрим далее возбуждение щелевой решетки волновыми пучками с разными амплитудными распределениями вдоль оси 0у.
2. Возбуждение решетки волновым пучком с равномерным амплитудным распределением
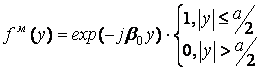 ,
(18)
,
(18) ,
,
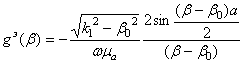 . (19)
. (19) (20)
(20) (21)
(21) , (23)
, (23) (24)
(24) (25)
(25)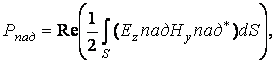
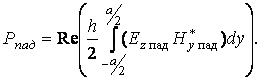 (26)
(26) (27)
(27)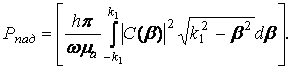 (28)
(28) 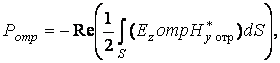 (29)
(29) (30)
(30)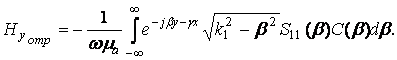 (31)
(31)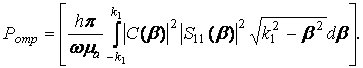 (32)
(32)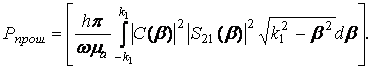 (33)
(33) , (34)
, (34) 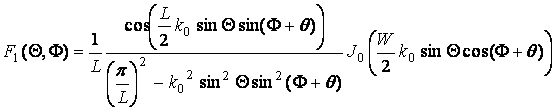
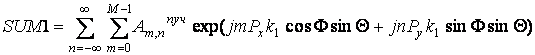
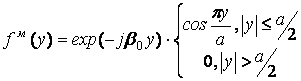 (35)
(35) ,
(36)
,
(36)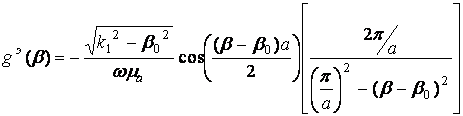 . (37)
. (37)  (38)
(38)