Алгоритм получения коротких сферических кодов на основе троек Штейнера
А. С. Чернышев
НовГУ имени Ярослава
Мудрого
Получена 15 февраля 2008 г.
В статье проведен анализ структуры двух сферических кодов, на основе которого разработан алгоритм вычисления кодов большей длины. Также проведено сравнение помехоустойчивости полученных сферических кодов и известных блоковых кодов.
Рассмотрим задачу передачи сообщений с минимальной задержкой по гауссовскому каналу. Для ее решения необходимо использовать коды, имеющие минимальное время декодирования. Очевидно, что в данном случае подходят только короткие блоковые коды, например БЧХ или Голея. Сферические коды небольшой длины также могут применяться для решения данной задачи.
В [1] описан алгоритм вычисления сферических кодов, с помощью которого были получены некоторые симметричные сферические коды с параметрами, представленными в таблице 1.
Длина сигналов ансамбля (n)
Количество сигналов в ансамбле (m)
Относительная скорость (R)
Минимальная дистанция (rmin)
Максимальный коэффициент корреляции
6
27
0.792
1.2247=
0.25
7
56
0.830
1.1546=
0.333
8
72
0.771
1.1339=
0.357
9
96
0.732
1.1546=
0.333
10
40
0.532
1.2910=
0.167
Вычисление кодов с длиной более 10 c помощью данного алгоритма требует значительно больших вычислительных затрат. Для поиска более длинных кодов разработан новый алгоритм, представленный в настоящей работе.
Для оптимизации процесса вычисления необходимо подробно исследовать структуру и свойства уже найденных кодов. Из таблицы 1 видно, что коды длины 7 и 9 имеют одинаковую минимальную дистанцию между точками
. Этот указывает на то, что данные коды могут иметь похожую структуру.
Чтобы выяснить пространственную структуру сигнала, определим расположение ближайших точек сигнала. Выберем любую точку сигнала и найдем все точки, отстоящие от нее на расстоянии
. Количество таких соседних точек будет 27 и 39 для кодов
и
соответственно. Далее найдем углы между вектором выбранного сигнала и векторами соседних сигналов:
, (1)
где
- вектор сигнала с номером
,
- его i-ая координата.
Вычислив данные углы, получаем одинаковый результат
для всех
В данном случае ребрам куба будут соответствовать вектора, начинающиеся в выбранной точке с концами во всех остальных точках сигнала. Найдем углы между каждой парой таких векторов:
(2)
Анализ результатов показывают, что из всего множества m-1 векторов можно выбрать n таких, которые попарно образуют углы 90°, т.е. ортогональных. Так как n определяет размерность пространства, то полученные векторы задают направление осей системы координат. Преобразуем все точки сигнала в новые координаты:
,
,
, (3)
где
- координаты точки в новой системе,
- исходные координаты точки,
- координаты базисных векторов.
Результаты преобразования координат для кода длины 7 приведены в таблице 2. Для удобства сигналы нормированы так, чтобы значения координат были равны ±1. Каждый столбец таблицы задает координаты 8 точек сигнала, отличающихся знаками координат. Именно эти группы точек образуют трехмерные кубы в n-мерном пространстве. Центры кубов расположены в начале координат.
X1
±1
0
0
±1
±1
0
0
X2
±1
0
±1
0
0
±1
0
X3
±1
±1
0
0
0
0
±1
X4
0
±1
±1
0
±1
0
0
X5
0
±1
0
±1
0
±1
0
X6
0
0
±1
±1
0
0
±1
X7
0
0
0
0
±1
±1
±1
Таким образом, после преобразования каждый сигнал кода имеет только три ненулевые координаты, а каждый отсчет сигнала только три уровня по амплитуде. Особенностью системы сигналов является то, что минимальное расстояние между точками сигналов внутри кубов равно минимальному расстоянию между точками разных кубов. В первом случае очевидно, что оно равно длине ребра куба, т.е.
. Как можно заметить из таблицы, ближайшими точками из разных кубов будут те, которые имеют одну одинаковую ненулевую координату и отличаются четырьмя координатами. Тогда минимальное расстояние будет:
. (4)
Данное свойство повышает плотность упаковки сигнала, т.к. при такой конфигурации увеличивается количество соседних точек вокруг одной точки. В результате возрастает помехоустойчивость.
Из таблицы 1 и приведенных выше свойств можно вывести правило, по которому должны строится сигналы с аналогичной структурой. Сигнал полностью определяется матрицей, имеющей
строк и
столбцов. Так как каждый столбец задает 8 сигналов, отличающихся знаками, то достаточно знать номера строк ненулевых элементов. Таким образом, элементы матрицы, соответствующие ненулевым координатам, будут равны единице, остальные – нулю.
Каждый столбец матрицы должен содержать ровно три единицы. Это правило следует из определения сферического кода, по которому расстояния от всех точек до центра должны быть равны. Кроме того, любая пара столбцов должны иметь не более одной общей единицы. В противном случае код будет содержать пару точек с расстоянием, меньшим
.
Данные условия соответствуют задаче вычисления неполной уравновешенной блок-схемы в комбинаторике [2]. Описанная выше матрица соответствует матрице инцидентности этой блок-схемы. Она определяется следующими пятью параметрами: количество элементов
соответствует размерности пространства n, количество блоков
- количеству кубов в сигнале
определяет, во скольких блоках появляется каждая пара элементов. В данном случае он равен 1, так как это соответствует условию
. Параметр
определяет, во скольких блоках появляется каждый элемент. Он принимает значения 3 и 4 для кодов с n=7 и n=9, соответственно.
Из определения блок-схемы следуют следующие соотношения между ее параметрами:
(5)
(6)
Подставим в эти уравнения параметры кода и примем
и
(7)
(8)
Выразим неизвестные параметры через размерность пространства
(9)
(10)
(11)
Блок-схемы с параметрами
называются системами троек Штейнера. Для таких блок-схем известны условия, достаточные для их существования, а также методы построения. Рассматриваемым кодам соответствуют именно такие системы, поэтому возможно вычислить коды длины
(12)
Подставим возможные
приведены в таблице 2. Относительная скорость кода определяется из выражения:
(13)
Как видно из таблицы 3, скорость
убывает с ростом длины кода. Для всех кодов минимальное расстояние
, при условии, что они лежат на единичной сфере.
n
7
9
13
15
19
21
25
27
31
33
37
39
m
56
96
208
280
456
560
800
936
1240
1408
1776
1976
R
0,83
0,73
0,59
0,54
0,465
0,43
0,39
0,37
0,33
0,32
0,29
0,28
Чтобы вычислить эти коды, необходимо найти соответствующие системы троек. Для этого был использован рекурсивный метод Мура [2]. Он позволяет найти систему порядка
, если известна система порядка
и система порядка
, содержащая подсистему порядка
. Таким образом, если известны системы порядка 7, 9 и 13, то можно последовательно вычислить все системы больших порядков. Далее из каждого столбца матрицы инцидентности получаются по 8 сигналов кода.
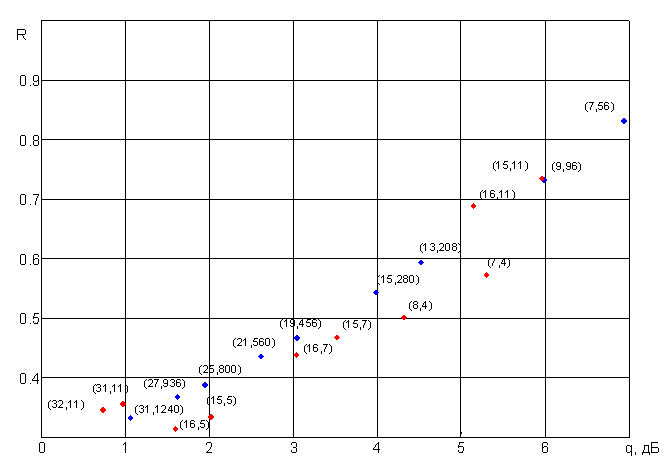
На рис.1 представлены результаты вычисления помехоустойчивости для полученных сферических кодов. Каждая точка на графике соответствует одному коду, а ее координаты R и q являются его характеристиками. R определяет скорость кода, а q – соотношение сигнал/шум, при котором вероятность ошибки приема сигнала равна
. Ошибка рассчитывается для случая передачи информации по гауссовскому каналу. Помехоустойчивость рассчитывалась при условии оптимального приема сигналов с помощью коррелятора. Для двоичных кодов ошибкой считался неправильный прием целого блока.
Кроме полученных кодов для сравнения приведены результаты для кодов БЧХ и расширенных кодов БЧХ, так как они являются наиболее эффективными короткими блоковыми кодами. Красными точками обозначены результаты двоичных кодов. В скобках приведены их параметры: длина кода
.
Рис. 1. Сравнение помехоустойчивости кодов.
Из графика видно, что напрямую можно сравнить результаты только нескольких кодов, так как остальные имеют разную длину и скорость. Код БЧХ (15,11) имеет практически равную помехоустойчивость и скорость со сферическим кодом (9,96). При этом последний имеет на 40% меньшую длину. Поэтому в некоторых задачах его применение будет предпочтительнее.
Сферический код (19,456) имеет на 0,48дБ большую помехоустойчивость относительно кода БЧХ (15,7) при равной скорости. Этот же код (19,456) оказывается эффективнее кода БЧХ (16,7) по скорости на 5,8% при близкой помехоустойчивости. В обоих случаях более эффективный код имеет несколько большую длину.
Код БЧХ (31,11) оказывается эффективнее на 7% скорости и 0,09 дБ, чем сферический код (31,1240). Длина кодов в данном случае одинаковая.
Из приведенного сравнения можно сделать вывод, что полученные коды оказываются более эффективными по сравнению с двоичными кодами при больших скоростях кода и меньшей длине. При длине порядка 31 их эффективность снижается. Поэтому данные сферические коды могут успешно применяться в системах, где требуется минимальная задержка на передачу и декодирование сигналов.
В [3] приведен список известных сферических кодов. Из перечисленных в таблице 3 в нем присутствует только код с параметрами (7,56), остальные в списке известных отсутствуют и являются новыми.
Список литературы
1. Чернышев А.С. Известия высших учебных заведений России. Радиоэлектроника. 2007. Вып. 4. С. 31-35.
2. Холл М. Комбинаторика. М.: Мир, 1970. 424с
3. N. J. A. Sloane, Spherical Codes. Nice arrangements of points on a sphere in various dimensions. http://www.research.att.com/~njas/packings/
