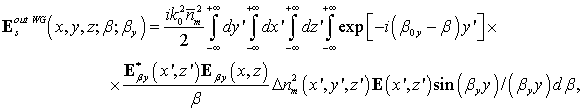“ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ” N 2, 2012

оглавление

УДК 517: 519.6: 535+537.8: 621.37

PACS: 02.30.Uu, 02.30.Zz, 02.50.Ey, 03.65.Db, 03.65.Nk, 42.25.Fx, 42.82.-m

 

 Использование параллельных процедур для ускорения расчетов электромагнитного поля лазерного излучения, рассеянного в интегрально-оптическом волноводе с трехмерными неоднородностями

 

А. А. Егоров,1 А. В. Ставцев2

1 Институт общей физики им. А.М. Прохорова РАН, Москва

2 Российский университет дружбы народов, Факультет физико-математических и естественных наук, Москва

 

Получена 22 февраля 2012 г.

 

Аннотация. Статья посвящена разработке методов и алгоритмов высокоэффективного численного решения актуальных задач векторного волноводного трехмерного рассеяния, требующих больших вычислительных ресурсов и больших ресурсов памяти. Для примера рассмотрена задача рассеяния собственных мод лазерного излучения на 3D-неоднородностях сред трехслойного интегрально-оптического волновода. Полученное ранее теоретическое решение данной электродинамической проблемы именно в интегральной форме позволило максимально эффективно реализовать численное решение поставленной задачи. С этой целью мы осуществили параллельную реализацию программного модуля для вычисления поля излучения вне волновода в двух видах. Использование методов параллельного программирования позволило нам достичь значительного увеличения скорости расчетов. В статье приведены: схема организации вычислений в случае N вычислительных узлов, с одним потоком на каждом узле; схема многопотоковой версии на базе одного компьютера с многоядерным процессором. Для реализации параллельной версии алгоритма программы расчета амплитуды напряженности электромагнитного поля вне волновода мы сделали реализацию программы на языке С++ с использованием библиотеки параллельного программирования MPICH. Использование методов параллельного программирования позволило нам достичь значительного увеличения скорости расчетов.

Ключевые слова: оптический волновод, направляемые и излучательные моды, дисперсионное соотношение, трехмерные нерегулярности, волноводное рассеяние, численное моделирование, компьютерный эксперимент, FDTD-метод, параллельное программирование, кластер, расчеты в многопотоковом режиме.

Abstract. Paper is devoted to developing methods and algorithms for high-performance numerical solution of topical problems of vector waveguide three-dimensional scattering, requiring large computational resources and more memory. As an example, we consider the scattering problem of modes of the laser radiation on the 3D-inhomogeneities of the medium of three-layer integrated-optical waveguide. Previously obtained theoretical solution of the electrodynamic problem in integral form permits effectively implement the numerical solution of the problem. To this end, we implemented a parallel realization of the software module for the calculation of the radiation field outside the waveguide in two forms. Using the methods of parallel programming has allowed us to achieve a significant increase in computation speed. The paper presents: the scheme algorithms in the case of N compute nodes, with one thread on each node; an organizational chart of calculations in a multithreaded mode on basis of one computer with the multinuclear processor. To implement the parallel version of the program algorithm for calculating the amplitude of electromagnetic field outside the waveguide, we realized the program in C++ using the library for parallel programming MPICH. Using of the methods of parallel programming has allowed us to achieve a significant increase in the rate of calculations.

Keywords: optical waveguide, guided and radiation modes, dispersion relation, three-dimensional irregularities, waveguide scattering, numerical simulation, computer experiment, FDTD-method, parallel programming, cluster, calculations in the multithreaded mode.

  

Введение

Совершенствование и активное развитие численных методов исследования стимулируют повышенный интерес к разработке векторной теории распространения, трансформации и рассеяния электромагнитного излучения в трехмерных (3D) нерегулярных волноведущих структурах (интегрально-оптических, металлодиэлектрических и других). Решение этих проблем имеет основополагающее значение для развития перспективных нанотехнологий в интегральной оптике и волноводной нанофотонике.

Численное исследование трехмерных задач интегральной оптики часто сопряжено с созданием алгоритмов, производящих вычисления на сетках больших размерностей [1-19]. Такие алгоритмы, как правило, требуют огромных вычислительных ресурсов и больших ресурсов памяти. Вследствие чего, уже на начальных этапах решения задачи, когда выбираются методы и инструменты возникает необходимость поиска подходов и выбора способа решения, позволяющих максимально эффективно использовать доступные вычислительные ресурсы.

Решение электродинамической задачи волноводного 3D-рассеяния лазерного излучения позволяет в частности с высокой точностью определить коэффициент затухания, а также учесть влияние 3D-нерегулярностей структуры (неровностей границ раздела и/или неоднородностей показателя преломления) на характеристики рассеянного излучения и в частности на характеристики оптических интегральных схем.

Одним из наиболее широко применяемых методов расчета волн является метод FDTD (Finite-Difference Time-Domain) [4]. Между тем он обладает целым рядом недостатков, например, таких как: «численная дисперсия» (приводящая к ошибкам в определении фазовой скорости) и «численная анизотропия», при которой в сеточной модели волновые числа волн, распространяющихся в различных направлениях в изотропной области, различаются [1-5].

Известно также, что решение уравнений Максвелла FDTD-методом или его модификациями позволяет достаточно эффективно вычислять электромагнитное поле внутри некоторой ограниченной области пространства, например, в резонаторе, призме, дифракционной решетке и т.д. Если же необходим расчет электромагнитных полей на расстояниях от исследуемого объекта, излучающего или рассевающего электромагнитное поле, то использование даже модифицированного метода FDTD приводит к необходимости огромных объемов вычислений и, как следствие, к катастрофическому падению эффективности метода.

 

1.     Постановка задачи. Методы исследования

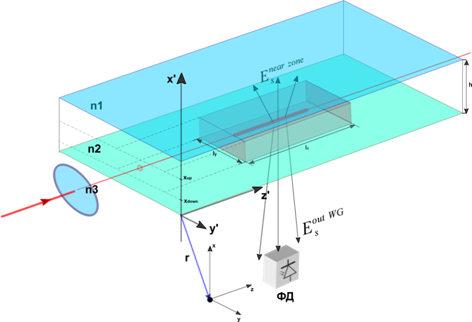
Объект исследования – нерегулярный оптический волновод с трехмерными нерегулярностями (см. рис. 1) [1, 3]. Нерегулярный волновод – волновод, у которого неровные границы раздела сред, образующих волновод, и/или неоднородная структура этих сред.

На рис. 1 схематично показано рассеяние лазерного излучения в интегрально-оптическом волноводе, нерегулярность которого обусловлена 3D-неоднородной структурой волноводного слоя.

 

 

Рис. 1. Геометрия задачи, иллюстрирующая рассеяние лазерного излучения в нерегулярном интегрально-оптическом волноводе:  – показатель преломления воздуха,  – показатель преломления волноводного слоя;  – показатель преломления подложки;  – толщина волноводного слоя; x, y, z и x', y', z' – координаты точки наблюдения и координаты точки, где расположена неоднородность волноводного слоя;  – радиус-вектор точки наблюдения;  – задают размеры неоднородной области.

 

В качестве примера задачи, требующей больших вычислительных ресурсов и больших ресурсов памяти, рассмотрим задачу рассеяния лазерного излучения на 3D-неоднородностях сред трехслойного интегрально-оптического волновода [1-3].

Рассматривается случай распространения в нерегулярном трехслойном планарном оптическом волноводе вдоль оси  первой четной (фундаментальной) направляемой (собственной) ТЕ0-моды с компонентами , , . Распространение и рассеяние других типов направляемых (собственных) ТЕ-мод, а также направляемых (собственных) ТМ-мод исследуется аналогично. Исследование рассеяния других типов мод, в том числе и рассмотрение вопросов особенностей рассеяния электромагнитных волн на других типах нерегулярностей, также интересующих экспериментаторов, выходит за рамки настоящей статьи и будет проведено в последующих работах.

В случае 3D-нерегулярностей любое распределение поля интегрально-оптического волновода представляем в виде разложения по всем возможным модам плоского волновода (по ортогональному набору (базисных) функций  и ) [1, 3, 7, 8, 14]:

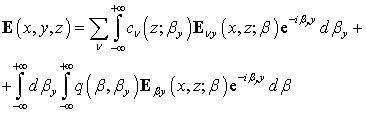.                     (1)

В выражении (1):  – коэффициенты разложения направляемых мод ;  – продольные составляющие постоянных распространения мод излучения (вдоль осей  и  соответственно);  – эффективная амплитуда рассеяния ТЕ-мод, определяемая как коэффициент разложения поля по всем модам излучения . Коэффициенты разложения ,  находятся с помощью известных соотношений ортогональности.

Теоретическое решение поставленной векторной электродинамической задачи рассеяния лазерного излучения в 3D-нерегулярном волноводе методом связанных мод в первом приближении теории возмущений было получено в работах [8-10]. Приближенное решение неоднородного векторного трехмерного волнового уравнения относительно поля излучения вне волновода, было найденного с помощью метода мод и метода функций Грина в интегральной форме (2), которая позволила максимально эффективно выполнять численное исследование поставленной задачи (см., например, [1, 3, 11]).

Полученное интегральное выражение для поля излучения  вне волновода (в отсутствии шума) можно записать в таком виде [1, 3, 8]:

 (2)

где  =  – модуль продольной составляющей  вектора распространения  фундаментальной направляемой ТЕ-моды вдоль оси ;  – коэффициента фазового замедления волновода;  – знак комплексно-сопряженной величины,  и  – координаты точки наблюдения (например, в дальней зоне, где расположен фотоприемник; см. рис. 1) и координаты точки, где расположена нерегулярность;  – мнимая единица;  – модуль волнового вектора ,  – длина волны монохроматического света в вакууме;  – среднее значение показателя преломления -го слоя ( = 1, 2, 3);  – среднеквадратичное отклонение показателя преломления соответствующего слоя волновода от среднего значения; ,  – продольные составляющие постоянных распространения мод излучения (вдоль осей  и  соответственно), формирующих диаграмму рассеяния;  и  – поля направляемых (дискретный спектр) мод и мод излучения (непрерывный спектр) несимметричного (в общем случае , где  – показатель преломления сред, образующих трехслойный волновод,  – диэлектрическая проницаемость соответствующего слоя волновода);  – решение однородного невозмущенного трехмерного уравнения, описывающего распространение исследуемой направляемой моды в волноводе,  в случае распространения в волноводе ТЕ0-моды.

В расчетах пределы интегрирования в нелинейном «интеграле рассеяния» (2) по осям  ограничены главным образом реальными физическими размерами области, в которой распределена неоднородность, при этом: .

Для подробного знакомства с проблемами, возникающими при трехмерном векторном рассмотрении проблемы волноводного рассеяния электромагнитных волн, рекомендуем следующие работы [1-3, 7-19, 24, 26], а также цитированную там литературу.

 

2.     Параллельная реализация программного модуля для вычисления электромагнитного поля излучения вне волновода

Рассеяние основной ТЕ-моды происходит на протяженной объемной неоднородности (в теории диэлектрических и полых металлических волноводов такая нерегулярность называется вставкой) показателя преломления волноводного слоя исследуемого волновода.

Ранее мы исследовали особенности разработки алгоритмов и программ для расчета основных характеристик нерегулярных интегрально-оптических волноводов в системе визуального программирования Delphi без использования процедуры распараллеливания [1, 3, 11, 15, 17-19].

 

                          (а)                                                               (б)

                          (в)                                                               (г)

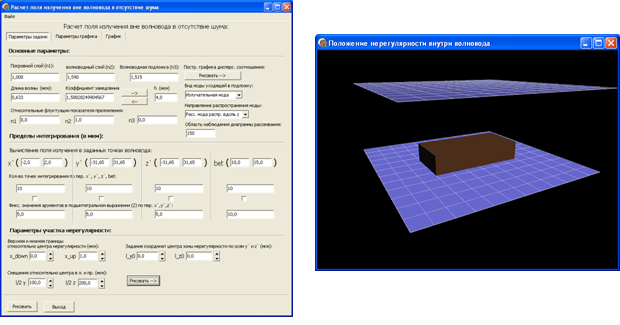
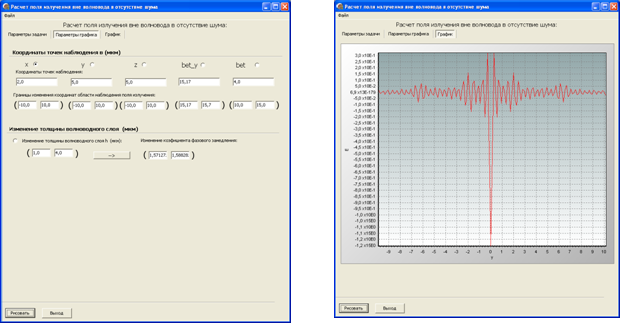
Рис. 2. Интерфейс программного модуля расчета напряженности поля, рассеянного в нерегулярном интегрально-оптическом волноводе.

 

На рис. 2 показан интерфейс программного модуля расчета напряженности поля в волноводе и вне него. На рис. 2а представлено диалоговое окно, в котором задаются входные параметры задачи: параметры волновода, область интегрирования, параметры нерегулярности и параметры лазерного излучения. На рис. 2б показана вкладка, на которой в режиме реального времени наглядно отображаются как свойства  нерегулярности (ширина, длина, высота), так и ее положение относительно слоев волновода. На рис. 2в представлено диалоговое окно, в котором задаются изменяемые параметры программы: промежутки изменения точек наблюдения , промежуток изменения постоянных распространения  мод излучения непрерывного спектра, промежуток изменение толщины волноводного слоя . На рис. 2г представлено диалоговое окно, в котором отображается полученная в результате расчета программы амплитуда поля излучения.

В результате проведенных численных экспериментов нами были получены следующие временные оценки (см., например, [1]). Количество точек разбиения по осям {β, x′, y′, z′}: β – 10 точек, x′ – 10 точек, y′ – 10 точек, z′ – 10 точек. Количество точек построения графика – 100 точек. Время построения амплитудно-фазовой диаграммы (заданного профиля поля ) – 3 секунды. Количество точек разбиения по осям {β, x′, y′, z′}: β – 100 точек, x′ – 100 точек, y′ – 100 точек, z′ – 100 точек. Количество точек построения графика – 100 точек. Время построения диаграммы рассеяния  – около 8 часов (оценка). Расчеты производились на персональном компьютере Intel Core 2 Duo со следующей конфигурацией: CPU Intel Core 2 Duo E6750, 2.66 ГГц, ОЗУ 2048 Мб.

Для сравнения аналогичные оценки были получены на другом персональном компьютере следующей конфигурации [3]: CPU Pentium 4, 3 ГГц, ОЗУ 2 Гб. Здесь были получены следующие результаты. Расстояние по оси : 50 мкм. Количество точек построения графика – 150 точек. Время построения одной диаграммы рассеяния составляет в среднем 10 секунд. При увеличении расстояния по оси  до 50 см и количества точек построения графика до 103 точек время счета одной диаграммы рассеяния  возрастает примерно до 2 минут. Здесь также выявлен значительный рост времени расчетов при существенном увеличении а) количество точек разбиения по осям {β, x′, y′, z′} и/или б) числа точек построения графика. Вместе с тем необходимо отметить, что в системе визуального программирования Delphi наша программа позволяют с точностью до 14-го знака после запятой получить численное решение задачи векторного волноводного рассеяния.

Как следствие проведенных многочисленных компьютерных экспериментов была установлена необходимость в значительных вычислительных ресурсах для эффективного численного решения проблемы рассеяния лазерного излучения направляемой моды на 3D-нерегулярности интегрально-оптического волновода.

К сожалению не всегда исследователи имеют доступ к специализированной вычислительной техники. Однако в ряде задач использование методов параллельного программирования позволяет достичь значительного увеличения скорости расчетов. Далее будут приведены схемы организации вычислений на базе типового учебного дисплейного класса, представляющего собой набор компьютеров, объединенных сетью Ethernet.

Математические программы, написанные с использованием «обычных» не узкоспециализированных компиляторов, часто не могут использовать архитектурные особенности современной вычислительной техники в полном объеме, проводя лишь минимальную оптимизацию машинного кода [17].

Так, например, подавляющее большинство современных процессоров имеет по несколько независимых вычислительных ядер, каждое из которых может обрабатывать по несколько независимых потоков. Однако если написать программу с использование такого компилятора «в лоб», то ускорение вычислений на многоядерном процессоре по сравнению с обычным одноядерным практически не будет заметно.

В будущем при наличии доступа к современной суперкомпьютерной технике, например, к вычислительным кластерам, те же самые подходы, несомненно, дадут намного больший эффект, но серьезных изменений в программе уже делать не придется. Поэтому целесообразно разработать подходы, которые позволили бы повысить скорость работы программы, максимально используя возможности современной вычислительной техники [20-22].

Система визуального программирования Delphi, на которой был написан первоначальный вариант программы, как раз относится к рассмотренным выше «обычным» не узкоспециализированных компиляторам. Более того, она не имеет никаких встроенных средств или программных интерфейсов, которые бы позволяли создавать параллельные программы, работающие на кластере. Поэтому для реализации параллельной версии алгоритма программы расчета амплитуды напряженности вне волновода мы сделали реализацию программы на языке С++ [23] с использованием библиотеки параллельного программирования MPICH [21].

Благодаря тому, что поле излучения  вне волновода получено в интегральной форме (2) удалось не только разработать эффективные численные алгоритмы, но и разработать их параллельную реализацию. Действительно, интегральная форма (2) обладает целым рядом преимуществ. Так, например область интегрирования можно разбить на отдельные сегменты и, затем, зная особенности поведения подынтегральных функций в каждом из сегментов, мы можем использовать на них разные методы интегрирования. Независимо от метода интегрирования, производить вычисления в каждой из подобластей можно независимо друг от друга.

Нами было опробовано несколько подходов для проведения расчетов в параллельном режиме [24]. Для расчета на кластере была реализована программа на языке С++, с использованием библиотеки параллельного программирования MPICH. Для простоты область интегрирования разбивается по одной из осей (например, по оси ) на равные сегменты, как это показано на рис. 3.

Такая схема наиболее проста, потому что практически не требует синхронизации или обмена данными между вычислительными потоками, при этом потери на накладные расходы минимальны. Каждый вычислительный поток, отработав свою порцию начальных данных, сохраняет полученный результат в файл. Все файлы с выходными данными в порядке разбиения сливаются в один итоговый файл.

Численные эксперименты проводились на базе дисплейного класса РУДН с  = 1, 2, 4 и 8 вычислительными узлами. Конфигурация узлов: CPU Pentium 4 2,4 ГГц, ОЗУ 512 Мб. Коммуникационная технология: Ethernet 100Мб/с. На рис. 4 представлена схема организации вычислений на базе типового дисплейного класса РУДН.

 

 

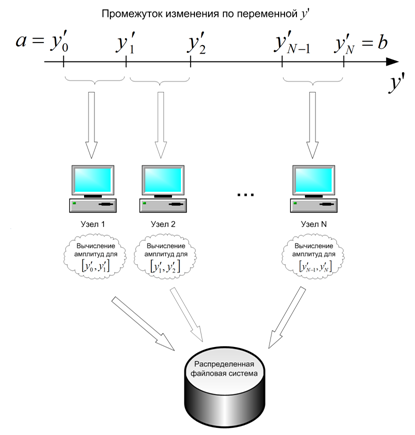
Рис. 3. Схема организации вычислений в случае N вычислительных узлов,

с одним потоком на каждом узле.

 

 

 

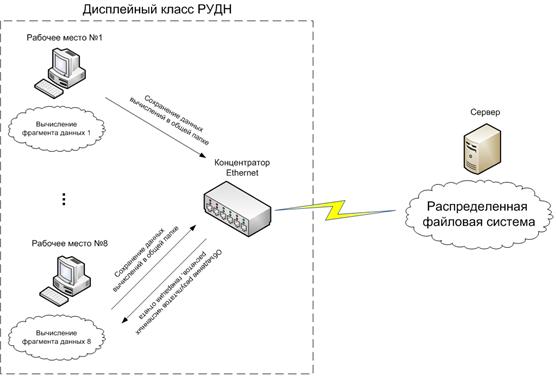
Рис. 4. Схема организации сети в типовом дисплейном классе РУДН.

 

Приведенная на рис. 4 схема организации параллельных вычислений на базе дисплейного класса РУДН достаточно очевидна и не требует дополнительных пояснений.

 

3.     Результаты численных расчетов. Выводы

Для примера рассмотрено рассеяние основной ТЕ-моды на протяженной объемной неоднородности (типа вставки) показателя преломления волноводного слоя полистиролового волновода. Трехслойный интегрально-оптический волновод образован тонким полистироловым слоем, нанесенным на стеклянную подложку.

При численном моделировании использовались следующие параметры гелий-неонового лазера: длина волны лазерного излучения  = 0.633 мкм, нормированная выходная мощность лазерного излучения  = 1. Параметры интегрально-оптического волновода (все для заданной ): показатель преломления воздуха (покровный слой)  = 1.000, показатель преломления волноводного слоя (полистироловая пленка)  = 1.590; показатель преломления подложки (стекло)  = 1.515.

Расчет полей производится от точки  = 0, расположенной на границе раздела пленка-подложка. Величина флуктуация неоднородности показателя преломления волноводного слоя составляла:  = 0.32 относительно подложки, и  = 1.24 относительно покровного слоя. Основное внимание в данной статье уделено расчетам двух зависимостей:  и , где  – некоторые фиксированные координаты.

Для упрощения численных расчетов полагалось, что 3D-неоднородность показателя преломления имеет квазипериодическое распределение неоднородности показателя преломления с единичной плотностью. Тип нерегулярности можно задать/модифицировать путем изменения вида функции , положения нерегулярности в волноводе, а также – размера интервала/области, в пределах которой проводится интегрирование в выражении (2).

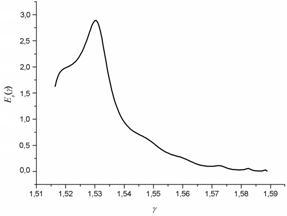
Для примера на рис. 5 приведены зависимости поля  от  (рис. 5а) и от  (рис. 5б) при заданных параметрах волновода и лазерного излучения гелий-неонового лазера ( = 0.633 мкм). Рисунок 5а в частности показывает с одной стороны особенности рассеяния направляемых (собственных) ТЕ-мод при достаточно большом коэффициенте  ( = 1.588282; ), а с другой – сложный нелинейный процесс трансформации поля излучения при его распространении от нерегулярной границы раздела пленка/воздух в окружающую среду: постепенный переход из примерно ближней зоны () в промежуточную зону (). Заметим, что максимум диаграммы рассеяния поля находится при значении  близком к точке перегиба на дисперсионной кривой [2].

На рис. 5б приведены: амплитуда поля , расчетная и экспериментальная интенсивности  рассеянного лазерного излучения ( = 0.63 мкм) направляемой (собственной) ТЕ-моды вне волноводного слоя в плоскости . Влияние шумовой компоненты снижено одинаковым эффективным сглаживанием экспериментальных и теоретических данных. Параметры волновода: коэффициент фазового замедления  = 1.584, толщина волноводного слоя  = 2.000 мкм. Размеры прямоугольной области нерегулярности:  мкм. Значения напряженности электрического поля рассеянного излучения на рис. 5 во всех случаях даны в произвольных единицах.

 

 

  

                          (а)                                                               (б)

Рис. 5. (а): Зависимость  от коэффициента фазового замедления . Толщина волновода  = 4 мкм. Высота неоднородности 1 мкм (расположена ниже границы раздела пленка/воздух). Координаты точки наблюдения: () = (10, 0, 0) мкм. (б): Расчетная и экспериментальная диаграммы рассеяния.

 

Важно подчеркнуть, что нелинейный «интеграл рассеяния» (2) описывает поле излучения на любом расстоянии от волновода, что позволяет использовать получаемые с его помощью результаты для совершенствования и оптимизации разнообразных экспериментальных исследований [3].

В экспериментах использовался метод волноводного рассеяния света [1-3, 8-11, 16-19, 25, 26]. Как видно из рис. 5б расчетная и экспериментальная диаграммы рассеяния достаточно хорошо соответствуют друг другу.

Результаты численных экспериментов при количестве  точек построения графика и количестве точек  интегрирования по каждому из направлений:

·        количество узлов  = 1: время вычисления  = 25 с;

·        количество узлов  = 2: время вычисления  = 15 с;

·        количество узлов  = 4: время вычисления  = 9 с;

·        количество узлов  = 8: время вычисления  = 5 с.

Как видно из полученных результатов мы получаем последовательное практически двукратное уменьшение времени вычисления при каждом двукратном увеличении количества узлов. Как мы отмечали выше, большинство современных процессоров обладают по  = 2–4 независимых ядер, где каждое ядро может обрабатывать по крайней мерее по 2 практически независимых потока. Поэтому представленный выше подход позволяет теоретически обеспечить 4–16 кратный прирост скорости вычисления (в зависимости от модели и архитектуры процессора) на каждом вычислительном узле по сравнению с не параллельным случаем.

С практической точки зрения при проведении предварительных расчетов не всегда удобно использовать «кластерную» версию программы, имеющую чисто консольный интерфейс, да и далеко не всегда есть свободный монопольный доступ к сети компьютеров. Поэтому помимо версии для расчета на кластере, мы разработали «многопотоковую» версию нашей основной программы для расчета полей излучения вне волновода на языке Delphi [1, 11].

На рис. 6 показана схема организации расчетов в многопотоковом режиме. Тестовые расчеты проводились на компьютере с  процессором Intel Core 2 Duo E6750, в котором имеются два независимых вычислительных ядра. Каждое из ядер данного компьютера может в практически параллельном режиме обрабатывать по 2 независимых потока.

Данный подход также показал хорошую эффективность. За счет использования многоядерной архитектуры процессора в нашей задаче при проведении тестовых расчетов удалось получить 2–8 кратный прирост скорости (в зависимости от модели и архитектуры процессора) вычисления по сравнению с не параллельным случаем. Отметим, что этот выигрыш получен на обычном персональном компьютере, на котором используется обычный «не узкоспециализированный» компилятор (который практически не может оптимизировать код программы под архитектуру процессора).

 

 

 

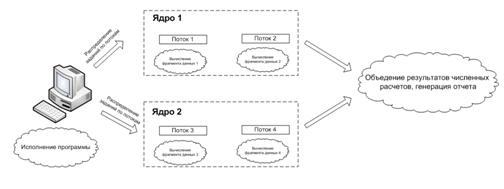
Рис. 6. Схема организации расчетов в многопотоковом режиме.

 

Рассмотренный выше метод расчета полей излучения вне волновода (особенно в дальней зоне) обладает рядом преимуществ:

·       обладает естественным параллелизмом,

·       масштабируется на любое количество вычислительных узлов,

·       обладает большой гибкостью (возможность применения разных численных методов, программных реализаций),

·       в отличие от существующих численных методов, таких как метод FDTD, не вносит численных искажений («численная дисперсия» и «численная анизотропия»).

С задачами создания алгоритмов, производящих вычисления на сетках больших размерностей сталкиваются при моделировании распространения и рассеяния направляемых (собственных) мод в нерегулярных волноведущих структурах [1, 3, 11, 15-19, 25, 26], при решении проблемы синтеза тонкопленочной обобщенной волноводной линзы Люнеберга [25], при расчете дифракционных тонкопленочных оптических структур методом связанных волн [27] и при решении ряда других подобных проблем. В свете этих проблем представленные в настоящей работе методы параллельных вычислений будут, несомненно, полезны.

 

Заключение

Дано краткое описание физической модели исследуемого явления, численного эксперимента, структуры алгоритма и его программной реализации. Приведены некоторые результаты численных расчетов, дан их анализ. Представлена схема организации параллельных вычислений на базе типовой сети дисплейного класса, а также схема многопотоковой версии на базе одного компьютера с многоядерным процессором, позволяющие эффективно ускорить численные расчеты электромагнитного поля лазерного излучения рассеянного в интегрально-оптическом волноводе с трехмерными неоднородностями. Таким образом, мы продемонстрировали возможность реализации альтернативных методов параллельного программирования в отсутствие доступа к специализированной вычислительной техники (суперкомпьютерные комплексы, супер-ЭВМ и др.). Очевидно, что в целом ряде задач использование таких методов параллельного программирования позволит достичь значительного увеличения скорости расчетов без привлечения сложной и дорогостоящей вычислительной техники.

 

Литература

1.      Егоров А.А., Ставцев А.В. Особенности разработки алгоритмов и программ для расчета основных характеристик нерегулярных интегрально-оптических волноводов // Вычислительные методы и программирование. 2010. 11, № 2. С. 31-39.

2.      Егоров А.А. Численное исследование характеристик лазерного излучения рассеянного в интегрально-оптическом волноводе с трехмерными неоднородностями // Оптика и спектроскопия. 2012. 112, № 2. С. 317-328.

3.      Егоров А.А. Теоретические, экспериментальные и численные методы исследования характеристик лазерного излучения рассеянного в интегрально-оптическом волноводе с трехмерными нерегулярностями // Квантовая Электроника. 2011. 41, № 7. С. 644-649.

4.      Taflove A., Hagness S.C. Computational electrodynamics: the finite difference time domain method, 2nd ed. London: Artech House, 2000.

5.       Хардиков В.В., Ярко Е.О., Просвирнин С.Л. Использование матриц передачи и псевдоспектрального метода во временной области для исследования дифракции света на планарных периодических структурах // Радиофизика и радиоастрономия. 2008. 13, № 2. 146-158.

6.      Хансперджер Р. Интегральная оптика: Теория и технология. – М.: Мир, 1985.

7.      Снайдер А., Лав Дж. Теория оптических волноводов. – М.: Радио и связь, 1987.

8.      Егоров А.А. Векторная теория рассеяния лазерного излучения в интегрально-оптическом волноводе с трехмерными нерегулярностями при наличии шума // Квантовая Электроника. 2004. 34, № 8. С. 744-754.

9.      Egorov A.A. Theory of laser radiation scattering in integrated optical waveguide with 3D-irregularities in presence of noise: vector consideration // Laser Physics Letters. 2004. 1, No. 12. С. 579-585.

10. Егоров А.А. Теория волноводного рассеяния света в интегрально-оптическом волноводе при наличии шума // Изв. Вузов. Радиофизика. 2005. 48, № 1. С. 63-75.

11. Егоров А.А., Ставцев А.В. Разработка и исследование комплекса программ для расчета основных характеристик интегрально-оптических волноводов в системе визуального программирования Delphi и С++ // Журнал Радиоэлектроники. 2009. № 8.

12. Маркузе Д. Оптические волноводы. – М.: Мир. 1974.

13. Унгер Х.Г. Планарные и волоконные оптические волноводы. – М.: Мир, 1980.

14. Содха М.С., Гхатак А.К. Неоднородные оптические волноводы. – М.: Связь, 1980.

15. Paulus M., Oliver J.F.M. A fully vectorial technique for scattering and propagation in three-dimensional stratified photonic structures // Optic. and QE. 2001. 33. С. 315-325.

16. Егоров А.А., Ставцев А.В. Разработка методов и алгоритмов расчета основных характеристик трехмерных нерегулярных интегрально-оптических волноводов // Вестник РУДН. Серия Математика. Информатика. Физика. 2010. № 2 (2). С. 139-151.

17. Егоров А.А., Ставцев А.В. Разработка комплекса программ для расчета основных характеристик трехмерных нерегулярных волноводов в пакете Borland Delphi версии 6.0 // Сб. докл. XII-й Науч. конфер. МГТУ “СТАНКИН”. 14 – 15 МАЯ 2009 г. М.: МГТУ “СТАНКИН”, С. 46-48.

18. Егоров А.А., Ставцев А.В. Разработка методов и алгоритмов расчёта основных характеристик трёхмерных нерегулярных волноводов // Труды 52-й научной конференции МФТИ «Современные проблемы фундаментальных и прикладных наук». Ч. VII., Т. 1. М.: МФТИ, 2009. С. 133-135.

19. Егоров А.А., Ставцев А.В. Компьютерные методы исследования характеристик трехмерных нерегулярных волноводов // Тезисы докладов XVII-й Международной конференции «МАТЕМАТИКА. КОМПЬЮТЕР. ОБРАЗОВАНИЕ». Дубна, 25 – 30 января 2010 г. Москва-Ижевск: РХД, С. 113.

20. Воеводин В.В., Воеводин Вл.В. Параллельные вычисления. – СПб.: БХВ-Петербург, 2002.

21. Антонов А.С. Параллельное программирование с использованием технологии MPI. – М.: Изд-во Московского университета, 2004.

22. Ставцев А.В. Построение классификации многокомпонентных вычислительных систем // Вестник РУДН. Прикладная и компьютерная математика. 2005. № 5. С. 126–134.

23. Страуструп Б. Язык программирования С++. Специальное издание. – М.: Бином, 2004.

24. Егоров А.А., Ставцев А.В. Параллельная реализация программного модуля для вычисления поля излучения вне волновода // Научная Сессия НИЯУ МИФИ-2012, г. Москва, 30 января – 4 февраля 2012 г., Конференция «Методы математической физики и математическое моделирование физических процессов». – М.: НИЯУ МИФИ, 2012, Т. 3, С. 141.

25. Егоров А.А., Ловецкий К.П., Севастьянов А.Л., Севастьянов Л.А. Моделирование направляемых (собственных) мод и синтез тонкопленочной обобщенной волноводной линзы Люнеберга в нулевом векторном приближении // Квантовая Электроника. 2010. 40, № 9. С. 830-836.

26. Egorov Alexandre, Sevastyanov Leonid. Propagation, transformation and scattering of the light in integrated-optical waveguides // SPIE Newsroom. DOI:10.1117/2.1201111.003860. 22 February 2012. pp. 1-3.

27. Егоров А.А., Ловецкий К.П., Севастьянов Л.А., Хохлов А.А. Метод связанных волн расчета дифракционных тонкопленочных оптических структур. Учебное пособие. – М.: Издат. Российского университета дружбы народов, 2011. – 164 с.