РАССЕЯНИЕ НА СТАТИСТИЧЕСКИ НЕРОВНОЙ ПОВЕРХНОСТИ С ПРОИЗВОЛЬНЫМИ КОРРЕЛЯЦИОННЫМИ СВОЙСТВАМИ
В. В. Ахияров
МГТУ им. Н.Э. Баумана
Получена 26 января 2012 г.
Аннотация. Рассмотрено решение задачи рассеяния на статистически неровной поверхности методом Монте-Карло. Представлен алгоритм формирования ансамбля поверхностей с требуемыми корреляционными свойствами. Приведены индикатрисы рассеяния на поверхностях с гауссовой и экспоненциальной функциями корреляции, а также на многомасштабной поверхности.
Ключевые слова: рассеяние радиоволн, метод Монте-Карло.
Abstract. The solution of scattering by a statistically rough surface using the Monte-Carlo method is considered. The formation technique of statistically rough surfaces with specified correlation function is presented. Scattering indicatrices for surfaces with Gaussian and exponential correlation functions, as well as for multiscale surface, are shown.
Keywords: radiowave scattering, Monte-Carlo simulation.
Как правило, задача рассеяния на статистически неровной поверхности решается методами статистической радиофизики (метод малых возмущений, метод касательной плоскости и т.д.). При этом полагается, что неровности являются гладкими и пологими, что соответствует гауссовой корреляционной функции рассеивающей поверхности [1]. Такая идеализация является удобной, но не всегда оправданной, поскольку в реальных условиях характер неровностей может быть произвольным. Поэтому в настоящее время для решения задачи рассеяния широко используется метод Монте-Карло, который заключается в численном решении задачи дифракции на ансамбле случайных поверхностей и статистической обработке полученных реализаций рассеянных волновых полей. По сравнению с методами статистической радиофизики такой подход является более универсальным, поскольку он не накладывает строгих ограничений на статистические характеристики рассеивающей поверхности.
В данной работе для простоты неровности поверхности считаются
цилиндрическими с образующими, параллельными оси Y (см. рис.1). Статистическими характеристиками такой поверхности являются среднеквадратичное отклонение (СКО) s относительно среднего
уровня ![]() , интервал корреляции l и корреляционная функция
, интервал корреляции l и корреляционная функция
![]() .
.
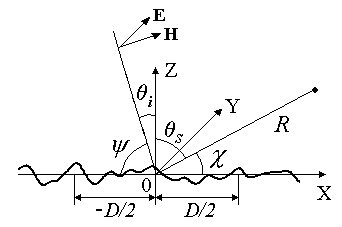
Рис.1. Геометрия задачи.
Каждую возможную реализацию рассеивающей поверхности можно
рассматривать как процесс на выходе фильтра с импульсной характеристикой ![]() , которая связана с
, которая связана с ![]() выражением [2]:
выражением [2]:
 . (1)
. (1)
Если на вход фильтра
подается белый шум ![]() с математическим ожиданием
с математическим ожиданием ![]() и СКО s, то функция случайных высот
определяется интегралом свертки [2]:
и СКО s, то функция случайных высот
определяется интегралом свертки [2]:
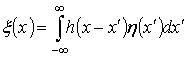 . (2)
. (2)
В области
пространственных частот свертка (2) соответствует произведению спектров
импульсной характеристики и белого шума. Поэтому формирование функции ![]() удобно выполнять с использованием
преобразования Фурье [3].
удобно выполнять с использованием
преобразования Фурье [3].
Рассмотрим алгоритм решения задачи дифракции на случайной идеально проводящей поверхности при горизонтальной поляризации падающего поля (ТЕ-поляризация). Для расчета поверхностной плотности тока используется скалярное интегральное уравнение Фредгольма первого рода [4, 5]:
 , (3)
, (3)
где ![]() – искомая плотность поверхностного
электрического тока,
– искомая плотность поверхностного
электрического тока, ![]() – падающее поле на рассеивающей
поверхности,
– падающее поле на рассеивающей
поверхности, ![]() – функция Ганкеля второго рода нулевого
порядка, x и x¢ – точки наблюдения и интегрирования,
– функция Ганкеля второго рода нулевого
порядка, x и x¢ – точки наблюдения и интегрирования,
![]() – волновое сопротивление свободного
пространства,
– волновое сопротивление свободного
пространства, ![]() – волновое число.
– волновое число.
В дальней зоне рассеянное поле определяется выражением [4, 5]:
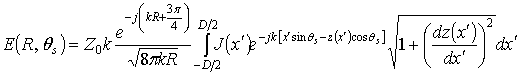 ,
(4)
,
(4)
где qs – угол рассеяния (см. рис.1).
Для ограничения области расчетов на интервале интегрирования ![]() поле источника моделируется волновым
пучком [6]:
поле источника моделируется волновым
пучком [6]:
![]() , (5)
, (5)
где qi – угол падения (от вертикали),
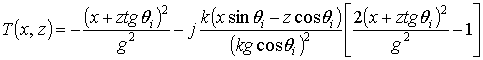 , (6)
, (6)
а параметр g выбирается в соответствии с условием:
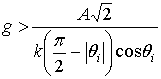 ,
,
![]() . (7)
. (7)
Решение задачи дифракции для ансамбля рассеивающих поверхностей позволяет определить коэффициент рассеяния [4]:
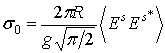 ,
(8)
,
(8)
а также коэффициенты когерентного и некогерентного рассеяния:
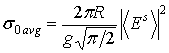 ,
(9.а)
,
(9.а)
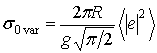 .
(9.б)
.
(9.б)
где
* – комплексное сопряжение, ![]() –
дисперсия флуктуаций рассеянного поля:
–
дисперсия флуктуаций рассеянного поля:
![]() .
.
Рассмотрим результаты решения задачи рассеяния для ансамблей поверхностей с гауссовой
![]() (10)
(10)
и экспоненциальной
![]() (11)
(11)
корреляционными функциями.
Необходимо отметить, что использование кривой Гаусса (10) дает удовлетворительное согласие с экспериментом при вычислении рассеянного поля только вблизи зеркальных углов. Использование экспоненциальной корреляционной функции в ряде случаев позволяет получить лучшее соответствие экспериментальных и теоретических результатов [1].
Высоты неровностей рассеивающих поверхностей полагаются малыми (в масштабе длины волны), т.е. выполняется критерий Релея [1]:
![]() ,
(12)
,
(12)
где x – высота отдельной неровности.
На рис.2 представлены
индикатрисы рассеяния на поверхности с гауссовой функцией корреляции для угла
падения ![]() (направление облучения здесь и далее на
всех рисунках показано стрелкой). Каждая поверхность размером
(направление облучения здесь и далее на
всех рисунках показано стрелкой). Каждая поверхность размером ![]() была сформирована из
была сформирована из ![]() значений случайных высот
значений случайных высот ![]() , СКО неровностей
, СКО неровностей ![]() ,
интервал корреляции
,
интервал корреляции ![]() , усреднение проводилось по
, усреднение проводилось по ![]() реализациям рассеянного поля (здесь и далее считаем, что единицей измерения D, s и l является длина электромагнитной волны).
реализациям рассеянного поля (здесь и далее считаем, что единицей измерения D, s и l является длина электромагнитной волны).

Рис.2. Индикатрисы рассеяния на поверхности с гауссовой
функцией корреляции при ![]() и
и
![]() .
.
Сплошная линия – ![]() , пунктир –
, пунктир – ![]() , точки –
, точки – ![]() .
.
Из представленного
рисунка видно, что рассеяние в зеркальном направлении обусловлено когерентной
составляющей ![]() , а форма индикатрисы некогерентного
рассеяния
, а форма индикатрисы некогерентного
рассеяния ![]() близка к гауссовой.
близка к гауссовой.
Результаты расчетов для
ансамбля поверхностей с экспоненциальной функцией корреляции представлены на
рис.3. Исходные данные – те же, что и в предыдущем случае: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Сравнение результатов,
представленных на рис.2 и рис.3, свидетельствует о том, амплитуда когерентной
составляющей
. Сравнение результатов,
представленных на рис.2 и рис.3, свидетельствует о том, амплитуда когерентной
составляющей ![]() в обоих случаях остается примерно постоянной,
а увеличение рассеяния в зеркальном направлении при экспоненциальной корреляции
обусловлено вкладом некогерентного рассеяния.
в обоих случаях остается примерно постоянной,
а увеличение рассеяния в зеркальном направлении при экспоненциальной корреляции
обусловлено вкладом некогерентного рассеяния.
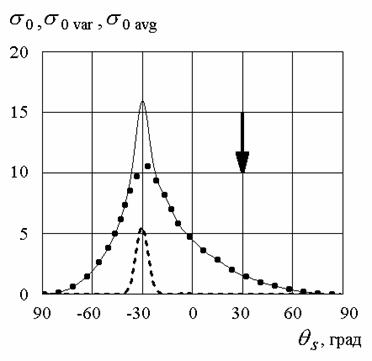
Рис.3. Индикатрисы рассеяния на поверхности с экспоненциальной
функцией корреляции при ![]() и
и
![]() .
.
Сплошная линия – ![]() , пунктир –
, пунктир – ![]() , точки –
, точки – ![]() .
.
Далее рассмотрим рассеяние на многомасштабной поверхности, обладающей свойством самоподобия. Ансамбль реализаций таких поверхностей формируется на основе функции Вейерштрасса:
 ,
(13)
,
(13)
где a —
произвольное нечетное число, ![]() .
.
На рис.4 показаны результаты
расчетов по формуле (13) при ![]() и
и ![]() на интервале
на интервале ![]() .
Видно, что увеличенный участок подобен всей функции, т.е. форма поверхности не
изменяется от того, рассматриваем мы ее вблизи или издалека. Следует отметить,
что данная функция является непрерывной и не дифференцируема ни в одной точке.
.
Видно, что увеличенный участок подобен всей функции, т.е. форма поверхности не
изменяется от того, рассматриваем мы ее вблизи или издалека. Следует отметить,
что данная функция является непрерывной и не дифференцируема ни в одной точке.

Рис.4. Функция Вейерштрасса.
Чтобы сформировать ансамбль
реализаций многмасштабных поверхностей, требуется вычислить корреляционную
функцию выражения (13). Для расчетов были выбраны следующие значения: ![]() ,
, ![]() ,
, ![]() и
и ![]() , при
этом можно ограничиться четырьмя членами ряда в формуле (13).
, при
этом можно ограничиться четырьмя членами ряда в формуле (13).
На рис.5 представлена
возможная реализация многомасштабной рассеивающей поверхности со значением СКО ![]() , на рис.6 – нормированная корреляционная
функция (сплошная кривая – исходная функция, кружки – расчеты для ансамбля из
, на рис.6 – нормированная корреляционная
функция (сплошная кривая – исходная функция, кружки – расчеты для ансамбля из ![]() реализаций). Видно, что исходная функция
и результаты моделирования практически совпадают.
реализаций). Видно, что исходная функция
и результаты моделирования практически совпадают.

Рис.5. Возможная реализация рассеивающей поверхности.
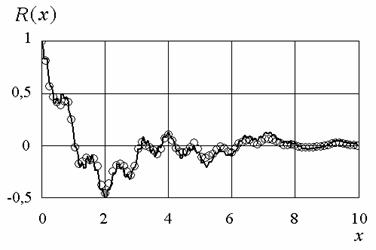
Рис.6. Нормированная корреляционная функция.
Сплошная линия – исходные данные, кружки – результат моделирования.
Далее были выполнены
расчеты коэффициентов рассеяния для ансамбля многомасштабных поверхностей при
углах падения ![]() (рис.7.а)
и
(рис.7.а)
и ![]() (рис.7.б). Поскольку неровности
являются малыми в масштабе длины волны, наблюдается интенсивное когерентное
рассеяние в зеркальном направлении.
(рис.7.б). Поскольку неровности
являются малыми в масштабе длины волны, наблюдается интенсивное когерентное
рассеяние в зеркальном направлении.

а)
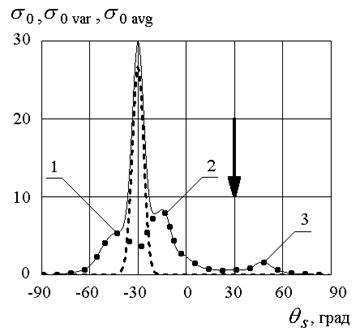
б)
Рис.7. Индикатрисы рассеяния при ![]() и
и
и различных углах падения: а – ![]() ; б –
; б – ![]() .
.
Сплошная линия – ![]() , пунктир –
, пунктир – ![]() , точки –
, точки – ![]() .
.
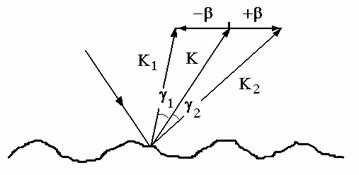
Рис.8. Брэгговское рассеяние на многомасштабной поверхности.
Индикатрисы некогерентного рассеяния имеют характерную
особенность в виде двух пиков, сдвинутых относительно зеркального направления
(на рис.7 они отмечены цифрами 1 и 2). Известно, что механизм
рассеяния на многомасштабной поверхности является брэгговским [7], а поскольку
исходная функция Вейерштрасса (13) была получена суммированием периодических
функций при различных значениях n, следует предположить,
что интенсивному некогерентному рассеянию соответствует ![]() .
На рис.8 представлена геометрия задачи с использованием следующих обозначений: g1, g2, K1 и K2 – отклонения от зеркального
направления и соответствующие волновые векторы, K – волновой вектор в
направлении зеркального рассеяния:
.
На рис.8 представлена геометрия задачи с использованием следующих обозначений: g1, g2, K1 и K2 – отклонения от зеркального
направления и соответствующие волновые векторы, K – волновой вектор в
направлении зеркального рассеяния:
![]() . (14)
. (14)
Вектор
![]() определяется соотношением:
определяется соотношением: ![]() , формула для определения его модуля приведена
в [7]:
, формула для определения его модуля приведена
в [7]: ![]() , тогда при
, тогда при ![]() получим
получим
![]() . Далее с использованием (14) можно
определить углы рассеяния g1 и g2. Проще всего это сделать
для случая
. Далее с использованием (14) можно
определить углы рассеяния g1 и g2. Проще всего это сделать
для случая ![]() :
: 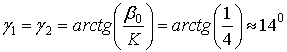 , что
примерно соответствует представленным на рис.7.а результатам.
, что
примерно соответствует представленным на рис.7.а результатам.
Помимо этого, при ![]() наблюдается еще один пик,
отмеченный цифрой 3 на рис.7.б. Поскольку его амплитуда меньше, чем у пиков 1 и
2, можно предположить, он соответствует случаю
наблюдается еще один пик,
отмеченный цифрой 3 на рис.7.б. Поскольку его амплитуда меньше, чем у пиков 1 и
2, можно предположить, он соответствует случаю ![]() , т.е.
рассеянию более высокого порядка.
, т.е.
рассеянию более высокого порядка.
Следует отметить, что индикатрисы рассеяния,
подобные представленным на рис.7.а, наблюдались экспериментально в оптическом
диапазоне [8]. Экспериментальные образцы рассеивающих поверхностей были созданы
искусственно: стеклянная пластина покрывалась фоторезистом, засвечивалась лазером
и далее на полученную спекл-структуру наносилось тонкое металлическое покрытие.
В ходе экспериментов при угле падения ![]() были
получены индикатрисы рассеяния с тремя пиками: центральным и двумя симметричными
относительно направления обратного рассеяния. Симметричные пики имели меньшую
амплитуду, а их отклонение от направления
были
получены индикатрисы рассеяния с тремя пиками: центральным и двумя симметричными
относительно направления обратного рассеяния. Симметричные пики имели меньшую
амплитуду, а их отклонение от направления ![]() находились
в пределах
находились
в пределах ![]() .
.
Представленные в данной работе результаты свидетельствуют о том, что метод Монте-Карло является эффективным инструментом для численного решения задачи рассеяния радиоволн и при его использовании практически не накладываются ограничения на статистические характеристики поверхности.
Литература
1. Басс Ф.Г., Фукс И.М. Рассеяние волн на статистически неровной поверхности. М.: Наука. 1972.
2. Левин Б.Р. Теоретические основы статистической радиотехники. Книга первая. М.: Сов. Радио. 1969.
3. Wagner R.I., Song J., Chew W.C. Monte Carlo Simulation of Electromagnetic Scattering from Tow-Dimentional Random Rough Surfaces // IEEE Trans. 1997. V. AP-45. No. 2. P. 235–245.
4. Axline R.M., Fung Adrian K. Numerical Computation of Scattering from a Perfectly Conducting Random Surface // IEEE Trans. 1978. V. AP-26. No. 3. P. 482–488.
5. Fung A.K., Chen M.F. Numerical Simulation of Scattering from Simple and Composite Random Surfaces // J. Opt. Soc. Am. A. 1985. V. 2. No. 12. P.2274–2284.
6. Toporkov J.V., Awadallah R.S., Brown G.S. Issues Related to the Use of a Gaussian-Like Incident Field for Low-Grazing-Angle Scattering // J. Opt. Soc. Am. A. 1999. V. 16. No. 1. P. 176-187.
7. Dwight L. J., Sun X. Scattering from fractally corrugated surface // J. Opt. Soc. Am. A. 1990. V. 7. No. 6. P. 1131-1139.
8. O’Donnell K.A., Mendez E.R. Experimental Study of Scattering from Characterized Random Surfaces // J. Opt. Soc. Am. A. 1987. V. 4. No. 7. P. 1194-1205.