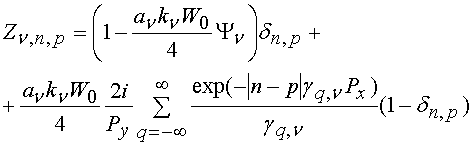УДК 621.396.67
МОДЕЛЬ НЕЛИНЕЙНОГО ИЗЛУЧАЮЩЕГО ЭЛЕКТРОМАГНИТНОГО КРИСТАЛЛА В СМЕСИТЕЛЬНОМ РЕЖИМЕ
С. Е. Банков1, М. Д. Дупленкова2
1 - ИРЭ им. В.А. Котельникова РАН, 2 – ОКБ МЭИ
Получена 1 февраля 2012 г.
Аннотация. Рассматривается излучающий электромагнитный кристалл, содержащий резистивно – емкостные нелинейные двухполюсники. Структура конечна по одной координате и бесконечна по другой и возбуждается плоской волной свободного пространства малой амплитуды на частоте сигнала. Одновременно электромагнитный кристалл возбуждается, распространяющейся в нем на частоте гетеродина собственной волной большой амплитуды. Рассмотрены две задачи нелинейного и линейного анализа. Нелинейный анализ проводится методом гармонического баланса, в рамках которого получается система нелинейных уравнений относительно амплитуд напряжений гармоник частоты гетеродина на всех элементах электромагнитного кристалла. Результат решения нелинейной задачи представляется в форме временных зависимостей дифференциальных проводимостей и емкостей нелинейных элементов. Линейный анализ структуры о воздействии на нее волны свободного пространства малой интенсивности проводится в предположении заданных дифференциальных проводимостей и емкостей. Результат решения линейной задачи – потери преобразования волны на частоте сигнала в волну электромагнитного кристалла на промежуточной частоте.
Ключевые слова: электромагнитный кристалл, нелинейный электромагнитный кристалл, метод гармонического баланса, потери преобразования.
Abstract. Radiating electromagnetic crystal containing resistive – capacitive non-linear two port elements is considered. The structure has a finite length along a coordinate axis and is infinite along another axis and it is excited by a free space plane wave with low amplitude that propagates at a signal frequency. Simultaneously the electromagnetic crystal is excited by its eigen mode with high amplitude that propagates at a heterodyne frequency. Two problems of linear and non-linear analysis are solved. Harmonic balance method is applied for solution of a non-linear problem. A system of non-linear equations relatively voltage amplitudes of heterodyne frequency harmonics at all elements of the crystal is obtained. The result of non-linear problem solution is presented in form of time dependencies of differential conductivities and capacities of non-linear elements. Linear analysis about excitation of the structure by a free space plane wave is carried out for given differential parameters. The result of linear analysis is loss of power transformation from signal frequency to intermediate frequency.
Keywords: electromagnetic crystal, non-linear electromagnetic crystal, harmonic balance method, transform loss.
1. Постановка задачи
Фотонные и электромагнитные кристаллы (ЭМК) привлекают внимание исследователей благодаря ряду необычных свойств, которые отличают их от «естественных» материалов [1].
В последнее время большой интерес вызывают нелинейные кристаллические структуры, в частности, двумерные структуры. Они рассматривались, например, в работах [2], [3] с использованием метода гармонического баланса. Близкий к указанным работам математический аппарат применялся для описания двумерных нелинейных антенных решеток [4]. Нелинейные решетки и двумерные излучающие кристаллы с нелинейными элементами представляют собой два класса объектов, которые имеют много общего. Тем не менее, между ними существует принципиальное отличие, заключающееся в том, что ЭМК представляет собой искусственную среду, в которой могут распространяться собственные волны. Благодаря этому возможно возникновение в ней эффектов накопления нелинейных взаимодействий, таких как пространственный синхронизм [5], который существенно усиливает такие эффекты как генерация кратных гармоник, параметрическое усиление и т.д.
Данная работа является продолжением работ [2] и [3], в которых исследуется взаимодействие волн свободного пространства с излучающим нелинейным ЭМК, а также работ [6 – 8], в которых анализируются неизлучающие структуры. Нашей целью является разработка математической модели, позволяющей анализировать излучающий ЭМК в режиме смешения сигналов, который представляет большой интерес с точки зрения построения приемных нелинейных остронаправленных антенн.
Излучающие ЭМК рассматривались в работах [2] и [3]. В обеих работах анализировался ЭМК на основе плоского волновода (ПВ) с решеткой металлических цилиндров, в которые включены нелинейные двухполюсники (см. рис. 1). Решетка имеет ограниченные размеры по оси 0х и бесконечна по оси 0у. Каждый из металлических цилиндров электрически связан с излучателем, в качестве которого может использоваться, например, печатная антенна, которая имеет выраженные резонансные свойства. В этом случае период структуры имеет вид, показанный на рис. 2. Смысл использования излучателей заключается в создании связи между волнами ЭМК и волнами свободного пространства.
Отличие между структурами, рассмотренными в работах [2] и [3] состоит в типе нелинейных элементов, включенных в металлические цилиндры. В работе [2] анализировались элементы с резистивно – емкостной, а в работе [3] с емкостной нелинейностью.
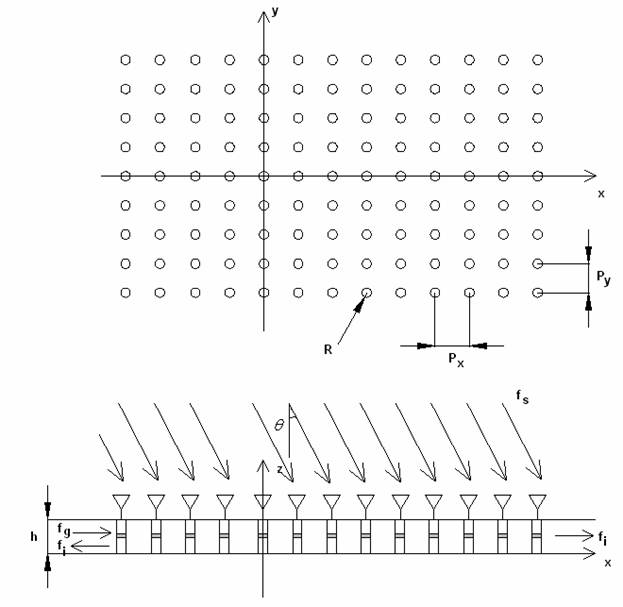
Рис. 1
Для ЭМК с емкостной нелинейностью характерны такие физические эффекты, как генерация кратных гармоник основной частоты и параметрические двух и трех частотное взаимодействие. Для ЭМК с резистивно – емкостной нелинейностью наибольший интерес представляет эффект преобразования частоты падающей волны в низкочастотный сигнал.
Рис. 2. Период исследуемой структуры.
В работе
[2], например, анализировался эффект детектирования волн свободного
пространства в нелинейном ЭМК. В режиме детектирования ЭМК возбуждается только
волнами свободного пространства на частоте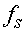 
,
которую назовем частотой сигнала.
Более сложным является
смесительный режим работы ЭМК. В этом режиме структура одновременно
возбуждается волнами на частотах 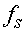и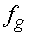 
. Назовем частоту 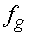частотой
гетеродина. Существенным обстоятельством является то, что мощность волны на
частоте 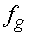(назовем ее волной гетеродина)
существенно превышает мощность волны на частоте сигнала (волна сигнала). Такое
соотношение между мощностями волн типично для смесительного режима.
Будем рассматривать случай возбуждения ЭМК на частоте гетеродина основной волной ПВ, падающей на ЭМК слева (см. рис. 1). Такой тип возбуждения оправдан с точки зрения использования ЭМК в качестве нелинейной антенны. В этом случае целесообразно рассматривать гетеродин как часть такой антенны, которая создает волну гетеродина внутри структуры. Основной функцией нелинейной антенны является прием слабого сигнала, поступающего на нее из свободного пространства.
Существенная разница между
мощностями сигналов на частотах и позволяет разделить единую задачу анализа
ЭМК на две задачи: нелинейную и линейную, как это обычно делается в практике
анализа смесителей [9].
На первом этапе решается нелинейная задача о
возбуждении ЭМК волной гетеродина. Результат ее решения состоит в определении
временных зависимостей токов и напряжений на нелинейных элементах ЭМК. На
втором этапе рассматривается возбуждение структуры слабым сигналом, поступающим
из свободного пространства. При этом структура считается линейной по сигналу,
но имеющей дифференциальные параметры, зависящие от времени. Дифференциальные
параметры находятся из нелинейного анализа. Решение линейной задачи позволяет
найти такие практически важные характеристики, как, например, потери
преобразования, характеризующие эффективность преобразования сигнала с частоты на промежуточную частоту 
, которая выражается через частоты и :
. (1)
При этом мы предполагаем, что волна на промежуточной частоте распространяется внутри ПВ и может быть известными средствами преобразована в направляемую волну коаксиальной, полосковой и т.д. линий передачи, которая формирует выход нелинейной антенны.
2. Допущения, при которых проводится анализ
В этом разделе мы опишем те ограничения, допущения и приближения, при которых будет анализироваться ЭМК. Первая группа допущений связана со структурой ЭМК. Будем рассматривать ЭМК, в котором отсутствуют тепловые потери во всех элементах за исключением нелинейных двухполюсников, которые принципиально являются источниками диссипации в силу резистивно – емкостного характера их нелинейности. Анализируемая структура имеет конечные размеры вдоль оси 0х и бесконечна вдоль оси 0у. Данная идеализация существенно упрощает формулировку и решение граничной задачи, так как периодичность ЭМК вдоль оси 0у позволяет использовать условия квазипериодичности поля по этой оси, которые с учетом нелинейного характера задачи сформулированы в работе [2].
Допущение о бесконечном по одной координате ЭМК
заставляет нас ограничить углы падения возбуждающих его волн. Будем
рассматривать падение сигнальных волн в плоскости XOZ.
В этом случае направление падения характеризуется одним углом 
. Считаем также, что гетеродинная волна
распространяется вдоль оси 0х и падает на границу ЭМК по нормали. Таким
образом, все возбуждающие ЭМК волны имеют однородное по оси 0у распределение
поля. Такое распределение поля исключает возникновение процессов накопления
вдоль оси 0у. Пространственный синхронизм может возникнуть только вдоль оси 0х
при определенном значении проекции волнового вектора сигнальной волны на ось
0х, которая зависит от угла . Проекция указанного
вектора на ось 0у равна нулю и поэтому в этом направлении синхронизм не
возникает. Таким образом, в рамках принятых ограничений на источники
возбуждения ЭМК волны в нем распространяются вдоль оси 0х, вдоль которой он
имеет конечные размеры. Такое положение позволяет учитывать влияние
ограниченных размеров ЭМК на развитие в нем волновых процессов.
Сформулируем далее ограничения на периоды ЭМК и высоту ПВ. Известно [6], что при увеличении периодов ЭМК или при увеличении частоты в структуре показанной на рис. 1 могут возникать распространяющиеся волны высших типов. Характер волновых явлений в многоволновом режиме существенно усложняется. Поэтому на первом этапе естественно ограничиться анализом исключительно одноволнового режима, при котором в ЭМК может распространяться одна собственная волна, которая излучает и принимает излучение из свободного пространства с одного направления.
Еще одно ограничение на параметры ЭМК связано с диаметром формирующих его цилиндров. Мы полагаем, что он является электрически малой величиной, причем на всех рассматриваемых в рамках нелинейного анализа частотах.
Рассмотрим далее ряд ограничений, связанных со свойствами излучателя. Мы рассматриваем узкополосные резонансные излучатели. Для определенности будем говорить о широко распространенных печатных антеннах, например четвертьволновых антеннах [10].
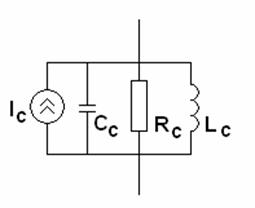
Рис. 3. Модель излучателя в виде параллельного контура.
Относительно своего входа такая антенна в окрестности резонансной частоты основного колебания может быть представлена в виде параллельного резонансного контура (см. рис. 3).
Источник тока 
моделирует возбуждение излучателя внешним
полем падающей волны. Считаем, что резонансная частота контура совпадает с
частотой сигнала , а его добротность 
велика настолько, что уже на частоте
гетеродина сопротивление контура пренебрежимо мало.
Кроме того, отметим, что первое колебание высшего типа в четвертьволновой
антенне имеет резонансную частоту приблизительно в три раза большую частоты
основного колебания. Поэтому сопротивление излучателя на второй гармонике
гетеродина также весьма мало.
С учетом сделанных выше замечаний мы можем утверждать, что гетеродин практически не взаимодействует с излучателем, так как он имеет пренебрежимо малое сопротивление на всех гармониках гетеродина вплоть до второй. Влиянием на распространение волны гетеродина излучателя на гармониках более высокого порядка мы будем пренебрегать.
Отметим, что в
работе [2] показано, что источник тока связан с параметрами ЭМК и мощностью
плоской волны 
, падающей на период структуры
следующим образом:
где 
-
коэффициент усиления излучателя, 
- волновое число
свободного пространства. Отметим, что максимальный коэффициент усиления 
апертурной антенны площадью 
описывается соотношением [11]:
, (3)
где 
-
длина волны в свободном пространстве. Коэффициент усиления (3) имеет площадка с
равномерным распределением источников. Источник тока 
,
соответствующий элементу решетки в виде идеальной антенны имеет следующий вид:
Нетрудно убедиться, что
максимальная мощность, которую можно передать от источника тока (4) в
согласованную с ним нагрузку равна мощности плоской волны, падающей на период
решетки .
Важно также отметить, что излучатели в общем случае связаны друг с другом через поля свободного пространства. Поэтому их надо рассматривать как единую антенную решетку. В рамках данной работы указанная связь имеет второстепенный характер. Поэтому мы не будем ее учитывать, а ограничимся простой моделью излучателя, которая описана выше.
В заключение обсуждения свойств излучателя отметим, что модель в виде эквивалентной схемы (см. рис. 3) позволяет рассматривать излучатель как сосредоточенное сопротивление, включенное в металлический цилиндр, аналогично нелинейному двухполюснику.
Ограничение на размеры цилиндров ЭМК позволяют использовать для описания его электродинамических свойств импедансную модель [6], в рамках которой реальный цилиндр с сосредоточенным элементом заменяется однородным по оси 0z цилиндром, на котором устанавливается следующее граничное условие:
, (5)
где 
-
радиус цилиндра, 
- тангенциальная компонента
магнитного поля на поверхности цилиндра, 
- z-ая компонента электрического поля, 
-
высота ПВ, 
- суммарный сосредоточенный импеданс,
включенный в цилиндр.
Соотношение (5)
имеет смысл закона Ома для цилиндра. При его записи было принято во внимание
то, что при 
( -
длина волны в среде внутри ПВ) электромагнитное поле однородно вдоль образующей
цилиндра. Кроме того, в силу однородности цилиндров по оси 0z
оно также не зависит от координаты z. С учетом этого
можно отметить, что в правой части выражения (5) стоит напряжение на цилиндре,
а в левой произведение тока на сопротивление. Равенство двух указанных величин
составляет содержание закона Ома.
Модель нелинейного двухполюсника возьмем в стандартной для СВЧ диодов форме [112]. Ей соответствует эквивалентная схема, показанная на рис. 4.
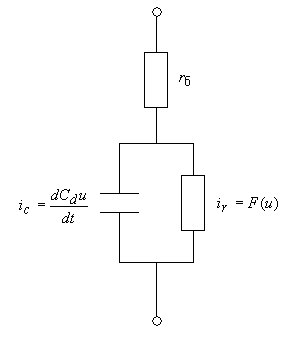
Рис. 4. Эквивалентная схема нелинейного двухполюсника.
Емкость диода 
зависит от напряжения на нем:
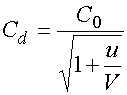, (6)
где 
-
напряжение пробоя.
Сопротивление диода описывается вольт – амперной характеристикой:
, (7)
,
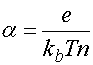где 
- постоянная
Больцмана, Т – абсолютная температура, 
-
заряд электрона, 
- параметр, зависящий от типа
диода, 
- обратный ток диода.
Важным моментом является связь диода с внешней схемой на постоянном и переменном токах.
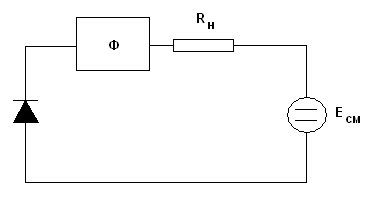
Рис. 5. Схема включения диода на постоянном токе.
На рис. 5 показана
схема включения диода на постоянном токе. Отметим, что сопротивление излучателя
согласно схеме на рис. 3 обращается в нуль. Также нулевое сопротивление имеет
металлический цилиндр, в который включен нелинейный двухполюсник. Связь диода с
внешней схемой происходит через фильтр, который на всех частотах, кроме нулевой
имеет бесконечное сопротивление и изолирует диод от сопротивления нагрузки 
и источника напряжения смещения 
. Поэтому период структуры на переменном
токе можно представить, как показано на рис. 6.
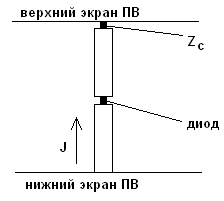
Рис. 6. Схема периода структуры на переменном токе.
На постоянном токе фильтр имеет нулевое сопротивление и соединяет диод с нагрузкой и источником смещения.
3. Нелинейный анализ ЭМК
Нелинейный анализ ЭМК сводится к задаче рассмотренной в работе [8], в которой рассматривался неизлучающий ЭМК, который возбуждался собственными волнами ПВ. Единственное отличие нашего случая состоит в типе нелинейного элемента, который в работе [8] имел емкостной характер. Однако это отличие не мешает нам непосредственно воспользоваться уравнениями, полученными в указанной работе.
В рамках нелинейного анализа сопротивление 
полагаем равным нулю (см. разд. 2).
Поэтому излучатель выпадает из анализа. Гетеродинная волна является основной Т
– волной ПВ, набегающей на ЭМК слева. Ниже без вывода приводятся уравнения из
работы [8]:
,
,
где
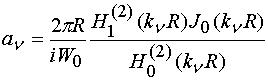, (9)
,
,
,
, 
,
,
,
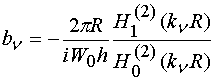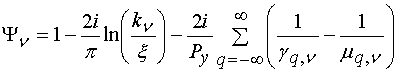где 
-
символ Кронекера, 
- волновое сопротивление среды
внутри ПВ, 
- волновое число свободного пространства
на частоте 
, 
-
высота ПВ, 
- периоды решетки ЭМК, 
- номер максимальной гармоники частоты
гетеродина, учитываемой в решении, 
- номер гармоники
гетеродина. Индексы 
описывают положение элемента
ЭМК по оси 0х. Вектора 
и 
имеют
размерность равную 
, где -
число цилиндров ЭМК по оси 0х. Их элементами соответственно являются токи,
текущие по цилиндрам ЭМК и напряжения на нелинейных двухполюсниках. Вектор 
имеет размерность 
,
а его элементами являются напряженности компоненты поля 
падающей
волны в центрах цилиндров ЭМК. При выводе соотношений (8) – (10) принято во
внимание, что в силу периодичности ЭМК по оси 0у, а также в силу описанного
выше способа возбуждения структуры, все поля являются периодическими функциями
координаты y.
Поле падающей волны описывается следующим образом:
. (11)
В уравнении (8) под 
понимается нелинейный оператор, связывающий гармоники тока с гармониками
напряжения на нелинейных двухполюсниках. В общем случае он имеет следующий вид:
(12)
.
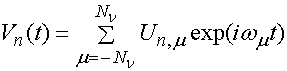В формуле (12) индекс - это номер элемента ЭМК, задающий его
положение на оси 0х, 
- нелинейная емкость, 
- ток через нелинейное сопротивление.
Благодаря оператору система
уравнений (8) становится нелинейной системой, которую в общем случае можно
решить только численными методами.
Следует отметить, что решение нелинейной системы (8)
представляет весьма непростую задачу. В работе [9] отмечается, что
вычислительный алгоритм, дающий устойчивое решение при нелинейном анализе
смесителя для произвольного сочетания параметров и начальных условий, неизвестен.
Данный вывод тем более актуален в нашем случае, в котором необходимо
анализировать одновременно 
нелинейных структур,
связанных друг с другом.
Для решения системы (8) мы использовали метод последовательных приближений, который сводится к следующему итерационному процессу:
где 
-
номер итерации. В качестве нулевого приближения используется следующий вектор:
, (14)
который соответствует решению для линейной структуры.
Сходимость
итерационного процесса показана на рис. 7, на котором представлены кривые
зависимости модуля первой гармоники напряжения на нелинейном элементе,
расположенном в цилиндре с нулевым номером 
- 
от номера итерации . Кривые 1 – 3 соответствуют разным
значениям полной мощности гетеродинной волны 
мВт.
Полную мощность гетеродина необходимо понимать следующим образом. Строго
говоря, она бесконечна, так как бесконечна по оси 0у анализируемая структура.
Поэтому правильно было бы говорить о мощности гетеродина, приходящейся на один
период ЭМК по оси 0у. Однако, интерес представляет также полная мощность
гетеродина, которая необходима для накачки структуры с реальными размерами. Для
ее оценки условно вводим размер ЭМК по оси 0у, характеризуя его числом
элементов по этой оси 
. При этом необходимо иметь
ввиду, что граничная задача решается для бесконечного ЭМК, а параметр используется только для расчета удельной
мощности 
, падающей на один период:
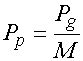. (15)
Кривые 1 – 3 получены для
следующих параметров, которые использовались также при построении кривых на
рис. 8 – 10: 
, 
, 
, 
, 
, 
, 
, 
.
Отметим, что здесь и далее все размеры приведены в миллиметрах, частоты в
гигагерцах, емкости в пикофарадах, напряжения в вольтах, токи в амперах, а
мощности в ваттах.
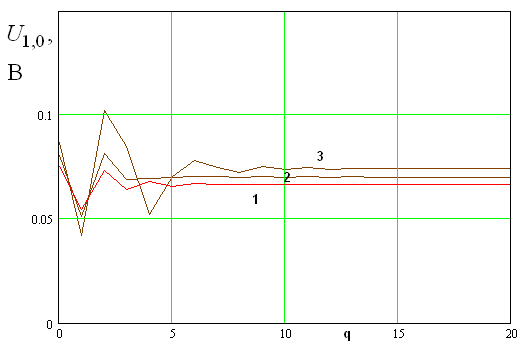
Рис.7. Зависимость напряжения на нелинейном элементе от номера итерации
Кривые 1 – 3
показывают основной недостаток итерационного процесса (13), заключающийся в
том, что он имеет колебательный характер. При этом амплитуда колебаний резко
растет с ростом интенсивности возбуждающего ЭМК воздействия. Для параметров
приведенных выше мощность 0.0465 является предельной, так как при ее повышении
решение расходится. Существенно на сходимость процесса влияет напряжение
смещения 
, увеличение которого также приводит к
расходимости решения.
Определенное улучшение ситуации может быть получено путем следующей модификации вычислительной схемы (13):
, (16)
где в качестве 
может использоваться достаточно
произвольно заданная монотонная действительная функция, которая меняется от
значения меньшего единицы при 
до единицы при 
. Применение функции позволяет сгладить зависимость напряжения
от номера за счет того, что возбуждающее
воздействие в начале итерационного процесса умышленно занижается, а затем оно
плавно приближается к номинальному значению.
Эффект сглаживания
итерационного процесса можно видеть из на рис. 9, на котором представлена
зависимость напряжения от номера итерации . Кривые на рис. 9 получены при
использовании функции следующего вида:
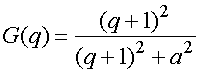, (17)
где 
-
параметр вычислительного процесса. Он выбирается исходя из численных
экспериментов. Кривые 1 – 5 на рис. 8 соответствуют следующим значениям
параметра 
0,0.5,1,2,2.5. Видно, что его увеличение
сглаживает поведение напряжения. При этом оно вне зависимости от значения стремится к одной и той же стационарной
величине.
Отметим, что
использование алгоритма (16) снижает риск расходимости. При этом скорость
сходимости может не только не увеличиваться, но и снижаться. Такое поведение
итерационного процесса связано с тем, что при увеличении параметра для приближения функции (17) к единице
необходимо увеличивать число шагов. При малых число
необходимых для выхода напряжения на стационарное значение шагов велико из-за
неустойчивости процесса. Поэтому мы можем ожидать существования минимума у
зависимости необходимого числа итераций 
от
параметра . Величина определяется
из следующего условия:
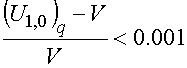, (18)
,
где
.
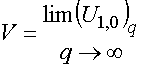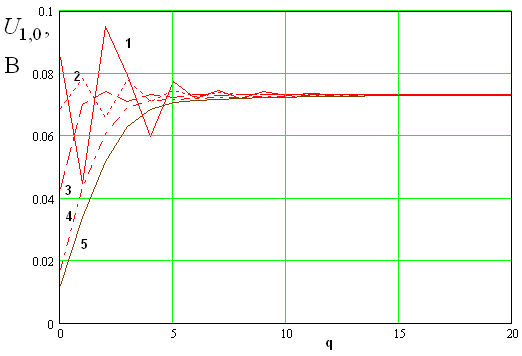
Рис. 8. Напряжение в зависимости от
номера итерации при разных .
Полученная численно
зависимость параметра от показана
на рис. 9. Кривая получена при 
(другие параметры ЭМК
приведены выше). Она подтверждает приведенное выше предположение о
существовании минимума функции 
, который
приблизительно находится при 
.
Рис. 9. Зависимость параметра от .
В заключение
обсуждения проблемы сходимости численного алгоритма рассмотрим кривые 1 – 6,
показанные на рис. 10. Они получены по алгоритму (16) при 
и соответствуют 
.
Из рис. 10 видно, что колебания итерационного процесса также появляются при
использовании алгоритма (16). Однако их появление с последующей расходимостью
процесса происходит при существенно большей мощности гетеродина, чем при
использовании алгоритма (13).
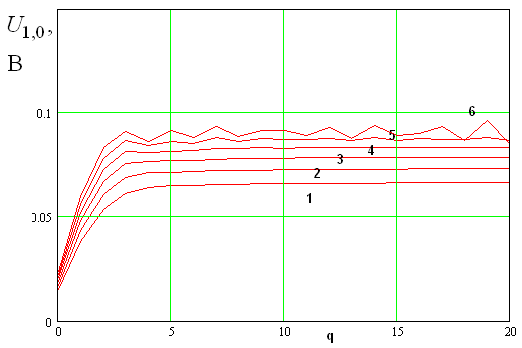
Рис. 10. Зависимость напряжения на нелинейном элементе от номера итерации при разной мощности гетеродина.
Из представленных выше результатов можно сделать вывод о том, что проблемы со сходимостью возникают преимущественно в том случае, когда напряжение на нелинейном элементе (диоде) велико настолько, что большую часть периода он открыт. Поэтому в рамках данной работы нам пришлось ограничиться исследованием структур, возбуждаемых гетеродинной волной сравнительно малой мощности при достаточно малых значениях напряжения смещения.
Забегая вперед, отметим, что
эффективность преобразования сигнала на промежуточную частоту сильно зависит от
формы тока, текущего через нелинейный элемент. Численные расчеты показали, что
максимальная эффективность достигается тогда, когда ток имеет форму короткого
импульса. Пример временной зависимости тока близкой к оптимальной показан на
рис. 11. Она получена при 
, 
. Остальные параметры ЭМК приведены выше.
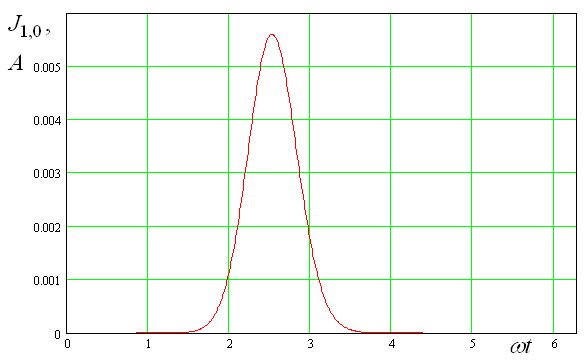
Рис. 11. Зависимость тока от времени.
4. Линейный анализ ЭМК
Линейный анализ ЭМК
проводим при стандартном для этого класса задач допущении о линейном поведении
структуры по отношению к сигналу. В этом случае нелинейный двухполюсник – диод
описывается в виде резистивно – емкостного элемента, у которого проводимость и
емкость зависят от времени. Проводимость 
является
дифференциальной проводимостью нелинейного сопротивления диода:
. (19)
Она находится по результатам решения
нелинейной задачи также как и емкость 
:
. (20)
Для определения параметров и в
соотношениях (19) и (20) необходимо использовать полученные в ходе решения
нелинейной задачи временные зависимости напряжения на диодах, входящих в ЭМК.
На рис. 12 показана модель периода ЭМК, полученная с учетом сделанных выше замечаний.
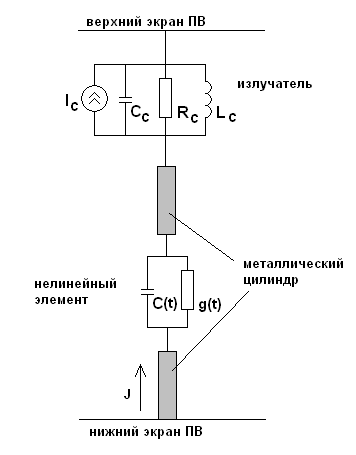
Рис. 12. Модель периода ЭМК для линейного анализа.
Взаимодействие сигнала с нелинейным двухполюсником приводит к появлению на нем напряжений комбинационных частот:
.
Отметим, что частоты 
связаны друг с другом следующим образом:
.
Поскольку напряжения и токи
сигналов на положительных и отрицательных частотах связаны операцией
комплексного сопряжения [9], то нам нет необходимости анализировать структуру
на всех частотах , а достаточно ограничиться,
например, частотами 
. Далее в данном разделе верхний
индекс + будем опускать. Также будем иметь в
виду, что индекс 
теперь соответствует не
гармоникам гетеродина, как это было выше, а напряжениям и токам на
комбинационных частотах .
Функции и являются
периодическими функциями с периодом 
равным 
. Поэтому их можно разложить в ряды Фурье:
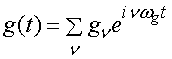, (23)
,
.
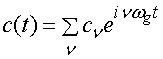Назовем параметры 
проводимостями преобразования, а 
емкостями преобразования. Гармоники тока,
текущего через нелинейный двухполюсник 
связаны
с гармониками напряжения 
следующим образом [9]:
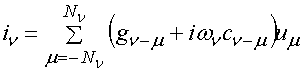. (24)
Соотношение (24) является
линейным оператором, который играет при решении линейной задачи роль
аналогичную оператору . Используя выражение (24), мы
можем записать систему уравнений, описывающую ЭМК при воздействии на него
слабого сигнала:
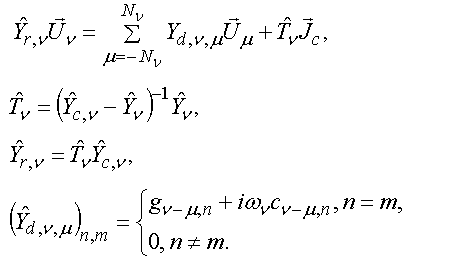(25)
В соотношениях (25) под 
понимается матрица, определенная
выражениями (8) – (10), 
- диагональная
матрица, у которой на главной диагонали стоят проводимости контуров,
моделирующих излучатели на соответствующих частотах 
,
вектор 
описывает внешнее по отношению к ЭМК
воздействие. Его элементами являются токи источников, входящих в эквивалентную
схему излучателя (см. рис. 12). Модули этих источников описываются соотношением
(2). Фазы зависят от номера элемента ЭМК :
, (26)
где 
-
волновое число свободного пространства на частоте сигнала, - угол падения плоской волны. Отметим,
что все матрицы, входящие в формулы (25) имеют размерность 
, где -
число элементов ЭМК вдоль оси 0х. Вектор имеет
размерность .
Следует обратить внимание на
то, что частота сигнала в обозначениях,
принятых в данном разделе является одной из частот 
.
Конкретное значения номера, который соответствует частоте сигнала, зависит от
соотношения между промежуточной частотой и частотой гетеродина:
, при 
, (27)
, при 
.
Нетрудно увидеть, что
система (25) является системой линейных алгебраических уравнений относительно
гармоник напряжения на нелинейных элементах. Она имеет размерность 
.
Смесительный режим
представляет интерес с точки зрения преобразования сигнала на промежуточную частоту.
В рамках допущений, сформулированных в разд. 2, вся энергия, выделенная
нелинейными элементами на частоте , аккумулируется внутри
ПВ в виде Т – волн, бегущих вдоль оси 0х в положительном и отрицательном
направлениях. Поэтому полезный эффект можно характеризовать мощностью Т – волн,
бегущих в ПВ на промежуточной частоте. Амплитуды электрического поля указанных
волн можно определить с помощью следующих соотношений, аналогичных соотношениям
из работы [6], использованных при определении параметров рассеяния ЭМК:
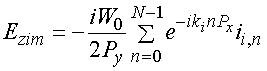, (28)
,
где 
-
волновое число свободного пространства на промежуточной частоте, 
- гармоника тока, текущего через -ый нелинейный элемент на промежуточной
частоте, 
- амплитуда волны, бегущей в
отрицательном направлении, а 
в положительном.
Символ 
здесь показывает, соответствие данной
величины промежуточной частоте. Отметим, что промежуточная частота также
является одной из частот . Она равна 
.
С помощью амплитуд 
можно найти мощности 
, которые переносят соответствующие волны
через сечение ПВ, имеющее по оси 0у длину равную периоду 
:
. (29)
Мощность сигнальной волны 
, приходящаяся на один период структуры по
оси 0у, определяется через введенный ранее параметр (см.
формулы (2) и (4)):
. (30)
Таким образом, мы можем с
помощью соотношений (29) и (30) найти парциальные потери преобразования 
:
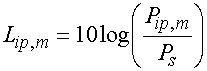, (31)
которые позволяют оценивать не только
энергетические характеристики ЭМК, но его направленность. Полные потери
преобразования 
определим как сумму парциальных
потерь:
. (32)
Аналогично мы можем ввести
потери преобразования на частоте сигнала: 
, 
, которые имеют смысл потерь
преобразования мощности волны свободного пространства в мощность направляемых
волн ЭМК.
5. Численное исследование ЭМК в смесительном режиме
Рассмотрим далее наиболее интересные результаты численного исследования ЭМК. Отметим, что анализируемая структура содержит весьма большое число свободных параметр, которые влияют на конечный результат. Поэтому полное исследование всех количественных закономерностей представляет весьма трудоемкую задачу, которая превосходит рамки данной работы. По этой причине мы остановимся лишь на некоторых важных особенностях смесительного режима работы ЭМК, которые удалось выявить в ходе его численного исследования.
Рассмотрим поведение
параметров 
, определяющих процесс преобразования
сигнала на промежуточную частоту. Отметим сразу, что в диапазоне исследованных
параметров нелинейные свойства емкости проявляются весьма слабо. В табл. 1
показаны значения емкостей 
, полученные для
первого элемента ЭМК с номером 
. Этот элемент наиболее
показателен с точки зрения оценки нелинейного взаимодействия, так как на него
падает гетеродинная волна с максимальной амплитудой. По мере прохождения через
ЭМК ее амплитуда уменьшается, так как часть ее энергии теряется в резистивных
элементах.
Данные в таблице. 1 получены
для следующих параметров: , , , , , , 
, , 
.
Таблица. 1.
|
|
-2 |
-1 |
0 |
1 |
2 |
|
|
0 |
0.00125 |
0.697 |
0.00125 |
0 |
Из таблицы.
1 видно, что наибольшее значение имеет нулевая гармоника емкости 
. Таким образом, напряжение на диоде слабо
меняет его емкость. Следовательно, его нелинейные свойства практически
полностью определяются активной частью проводимости.
На рис. 13 показана
зависимость модуля проводимости преобразования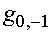 
,
которая играет основную роль при переносе частоты сигнала на промежуточную
частоту от номера элемента ЭМК. Кривые 1 – 3 получены для параметров указанных
выше за исключением напряжения смещения, которое соответственно равно 0.15,
0.175, 0.2 В. Видно, что три кривые отличаются друг от друга при сравнительно
малых . При увеличении номера они сливаются.
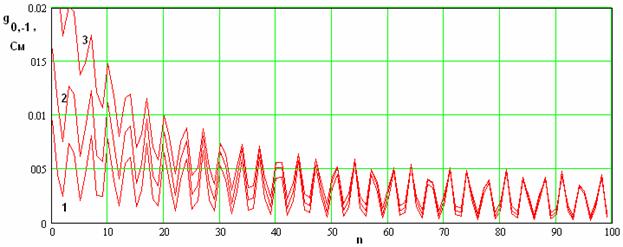
Рис. 13. Зависимость проводимости преобразования от номера элемента ЭМК.
На начальном участке средний уровень параметра 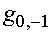меняется
по закону близкому к экспоненциальному, далее он стабилизируется и остается
неизменным. Частые осцилляции кривых обусловлены отражениями волн от концов
ЭМК. Отметим, что при относительно малых напряжениях смещения средний уровень
проводимости преобразования слабо меняется на длине ЭМК.
Представляет интерес
распределение фазы проводимости по длине ЭМК. Оно
показано на рис. 14.
Рис. 14. Распределение фазы проводимости преобразования в ЭМК.
Кривые 1,2 получены
для параметров приведенных выше (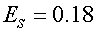). Кривая 1
соответствует фазе проводимости преобразования, а кривая 2 описывается
следующей функцией:
,
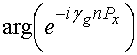где 
-
постоянная распространения волны ЭМК на частоте гетеродина . Из рис. 14 видно, что кривые 1 и 2 с
хорошей точностью совпадают друг с другом. Отсюда следует вывод о том, что фаза
проводимости преобразования почти полностью определяется фазой волны ЭМК на
частоте гетеродина. Данный вывод имеет важное значение для объяснения
следующего интересного результата, который был обнаружен в ходе численного
исследования.
Было установлено, что интенсивное преобразование мощности сигнала на промежуточною частоту происходит в условиях пространственного синхронизма трех волн, которые распространяются внутри ЭМК, а также волны свободного пространства, возбуждающей ЭМК. Говоря о трех волнах ЭМК, мы имеем в виду волну гетеродина, волну сигнала и волну промежуточной частоты. Все они являются собственными волнами ЭМК, существующими на соответствующих частотах.
Условия обнаруженного пространственного синхронизма имеют следующий вид:
,
где 
-
постоянные распространения собственных волн ЭМК на соответственно частотах 
. Второе условие из (33) имеет вид
типичный для антенн бегущей волны с быстрой волной. Волна ЭМК на частоте
сигнала является быстрой волной, у которой 
.
Данный вывод можно сделать из результатов работ [7], [8], в которых
рассматривались волны ЭМК.
Открытая структура с быстрой
волной эффективно излучает и принимает из свободного пространства энергию от
волн, распространяющихся под углом , который определяется
вторым равенством (33). Таким образом, выполнение данного соотношения
обеспечивает эффективное преобразование волны свободного пространства на
частоте в волну ЭМК на той же частоте. Этот
эффект имеет чисто антенную природу. Он никак не связан с нелинейными
свойствами структуры.
Первое равенство из (33)
связывает постоянные распространения собственных волн ЭМК на трех частотах. Его
природу нетрудно понять из обсуждавшейся выше зависимости фазы проводимости
преобразования от номера или координаты 
. Качественно ток промежуточной частоты
пропорционален произведению параметра на
напряжение 
на нелинейном элементе на частоте 
(отрицательная частота возникает из-за
того, что мы рассматриваем взаимодействие на частотах (см.
формулу (22))). Напряжение на частоте пропорционально
следующему множителю, который определяет его фазу:
.
Положительный знак в
показателе экспоненты связан с тем, что мы рассматриваем волну на отрицательной
частоте. Таким образом, ток промежуточной частоты 
пропорционален
следующей функции:
.
(34)
Указанные токи возбуждают волны ЭМК на промежуточной частоте. Фаза прямой волны, бегущей в положительном направлении оси 0х, в центрах цилиндров ЭМК определяется множителем:
. (35)
Таким образом, мы имеем волну токов (34) и собственную волну ЭМК (35). Известно [13], что наибольшая эффективность возбуждения собственной волны направляющей структуры волной тока наблюдается при совпадении их постоянных распространения, которое наблюдается при выполнении первого равенства из (33). Необходимо отметить, что в силу периодичности структуры эффективное возбуждение может наблюдаться при выполнении условия более общего вида. Однако в данной работе исследовалась ситуация, которая соответствует равенствам (33).
Рассмотрим далее поведение ЭМК в окрестности режима пространственного синхронизма. На рис. 15 показана зависимость потерь преобразования от угла падения сигнальной волны.
Рис. 15. Зависимость потерь преобразования от угла падения сигнальной волны.
Кривые 1 и 2 получены для
параметров приведенных в начале разд. 5. Они соответствуют параметрам 
и 
.
Отметим, что угол 
, при котором выполняются
условия (33) равен 9.650. Из рис. 1 видно, что положительное
значение угла падения соответствует распространению волны слева – направо.
Поэтому следует ожидать, что в ЭМК на частотах сигнала и промежуточной частоте
будут возбуждаться волны также бегущие слева – направо, то есть в положительном
направлении оси 0х. Поэтому потери 
существенно больше
потерь 
и мы их не
рассматриваем.
Из рис. 15 видно, что
зависимость потерь преобразования имеет максимум при угле падения равном . Кривые 1 и 2 можно рассматривать как
диаграммы направленности нелинейного ЭМК на сигнальной и промежуточной
частотах.
Направленные свойства ЭМК объясняет распределение амплитуд гармоник напряжения на нелинейных элементах вдоль оси 0х. Оно показано на рис. 16.
Рис. 16. Распределение модулей амплитуд гармоник напряжения вдоль оси 0х.
Кривые на рис. 16 получены
при выполнении равенства 
, остальные параметры
структуры приведены выше. Кривая 1 соответствует напряжению на частоте сигнала,
а кривая на промежуточной частоте. Видно, что амплитуды напряжений на обеих
частотах нарастают слева – направо, то есть в направлении распространения
падающей волны. Такое поведение напряжений приводит к тому, что преимущественно
в ЭМК возбуждаются волны, бегущие в положительном направлении. Поэтому мы
получаем указанное выше соотношение между потерями преобразования и .
Рис. 17. Зависимость потерь преобразования от частоты.
Первое равенство из (33)
выполняется на одной фиксированной частоте сигнала, которая при параметрах
указанных выше равна 7.5 ГГц. Исследуем зависимость потерь преобразования от
частоты. На рис. 17 представлена такая зависимость. Кривая 1 соответствует
параметру , а кривая 2 параметру . Кривые получены при фиксированном угле
падения, который равен 9.650. Видно, что они имеют резонансный
характер. Максимум достигается, когда выполняются условия синхронизма, то есть
на частоте 7.5 ГГц.
Заключение
Таким образом, мы можем сделать вывод о том, что пространственный синхронизм волн, распространяющихся в ЭМК на частотах сигнала, гетеродина и промежуточной частоте является важным фактором, обеспечивающим резкое повышение эффекта преобразования падающей на ЭМК сигнальной волны в направляемую волну ЭМК промежуточной частоты. Такой вывод делает актуальной задачу создания специальной аналитической модели ЭМК, позволяющей описывать и эффективно оптимизировать структуру в режиме пространственного синхронизма. Возможность перехода от систем уравнений типа (8) к более простым системам дифференциальных уравнений, описывающих ЭМК в режиме синхронизма, была показана в работах [3], [7], [8], в которых с их помощью исследовались явления генерации кратных гармоник и параметрического усиления. Можно предположить, что такой подход окажется эффективным также при исследовании явления смешения частот, о котором говорится в данной работе.
Литература
1. Банков С.Е. Электромагнитные кристаллы. М.: Физматлит. 2010.
2. Банков С.Е. Детектирование сигнала в излучающем нелинейном электромагнитном кристалле. [Электронный ресурс] // Журнал радиоэлектроники. 2012. №1. URL: http://jre.cplire.ru/jre/jan12/1/text.html
3. Банков С.Е. Численный анализ двухчастотного взаимодействия волн в излучающем нелинейном электромагнитном кристалле // РЭ. 2011. Т. 56. №9. С. 1044-1056.
4. Malyuskin A., Fusco V., Schuchinsky A. Microwave phase conjugation using nonlinerly loaded wire arrays // IEEE Trans. AP. 2006. V. 54. №1. P. 192-203.
5. Манцызов Б.И. Когерентная и нелинейная оптика фотонных кристаллов. М.: Физматлит. 2009.
6. Банков С.Е. Модель нелинейного электромагнитного кристалла // РЭ. 2011. Т.56. №3. С. 261.
7. Банков С.Е. Взаимодействие прямых волн в нелинейном электромагнитном кристалле. [Электронный ресурс] // Журнал радиоэлектроники. 2011. №3. URL: http://jre.cplire.ru/jre/mar11/1/text.html.
8. Банков С.Е. Численное исследование взаимодействия прямой и обратной волн в нелинейном электромагнитном кристалле // Успехи современной радиоэлектроники. 2011. №5. С. 31-43.
9. Розанов Б.А., Розанов С.Б. Приемники миллиметровых волн. М.: Радио и связь. 1989.
10. Панченко Б.А., Нефедов Е.И. Микрополосковые антенны // М.: Радио и связь. 1986.
11. Сазонов Д.М. Антенны и устройства СВЧ. М.: Высш. шк. 1988.
12. Гупта К., Гардж Р., Чадха Р. Машинное проектирование СВЧ устройств. М.: Радио и связь. 1987.
13. Вайнштейн Л.А. Электромагнитные волны. М.: Радио и связь. 1988.