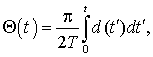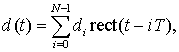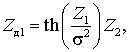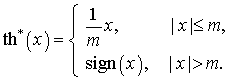АППРОКСИМАЦИЯ ОПТИМАЛЬНОЙ РЕШАЮЩЕЙ ФУНКЦИИ ДЛЯ АЛГОРИТМА ФАЗОВОГО ДИСКРИМИНИРОВАНИЯ ШУМОПОДОБНОГО MSK-СИГНАЛА
Е. В. Кузьмин
ФГАОУ ВПО «Сибирский федеральный университет», г. Красноярск
Получена 3 февраля 2012 г.
Аннотация. В статье исследуется квазиоптимальный алгоритм фазового дискриминирования шумоподобного MSK-сигнала. Обосновывается выбор крутизны аппроксимации решающей функции. Представлены результаты статистического моделирования.
Ключевые слова: шумоподобный сигнал, алгоритм фазового дискриминирования, дисперсия эквивалентных фазовых флуктуаций, MSK-модуляция.
Abstract. Quasi-optimal algorithm for the spread-spectrum MSK-signal phase discriminator is investigated. Choice of the approximation coefficient is proved. Results of statistical modeling are given.
Keywords: spread-spectrum signal, phase discrimination algorithm, equivalent phase fluctuations dispersion, minimum shift keying modulation.
В перспективных радионавигационных системах находят применение шумоподобные сигналы (ШПС) с минимальной частотной манипуляцией, в зарубежной литературе упоминаемые как MSK-signals (Minimum Shift Keying). Шумоподобные MSK-сигналы превосходят традиционные фазоманипулированные сигналы по спектральной эффективности и другим показателям [1]. Одной из главных проблем при приёме ШПС является осуществление фазовой синхронизации, что необходимо для когерентного корреляционного приёма и фазовых методов измерения координат места и параметров движения потребителей. Системам фазовой синхронизации (СФС) приёмников ШПС посвящено достаточно большое число работ, например [2], однако публикаций по фазовым дискриминаторам (ФД) ШПС-MSK – наиболее специфическим элементам СФС в настоящее время известно небольшое количество, к примеру [3, 4].
Цель данной статьи: обоснование крутизны аппроксимации оптимальной
по критерию максимального правдоподобия решающей функции ![]() для алгоритма фазового дискриминирования
шумоподобного MSK-сигнала.
для алгоритма фазового дискриминирования
шумоподобного MSK-сигнала.
Шумоподобный MSK-сигнал может быть представлен в комплексной форме [5]:
|
|
(1) |
где ![]() – комплексная огибающая;
– комплексная огибающая; ![]() – центральная частота;
– центральная частота; ![]() – начальная фаза;
– начальная фаза; ![]() – мощность сигнала;
– мощность сигнала; ![]() – информационный сигнал;
– информационный сигнал; ![]() – функция определяющая закон угловой
модуляции;
– функция определяющая закон угловой
модуляции; ![]() – псевдослучайная последовательность (ПСП)
длины
– псевдослучайная последовательность (ПСП)
длины ![]() ,
, ![]() –
длительность элемента ПСП,
–
длительность элемента ПСП, ![]() – прямоугольный
импульс длительности
– прямоугольный
импульс длительности ![]() .
.
Структурная
схема оптимального по критерию максимального правдоподобия ФД представлена на
рис. 1, где введены обозначения: ![]() – перемножитель;
– перемножитель; ![]() – интегратор, опрашиваемый в моменты
времени
– интегратор, опрашиваемый в моменты
времени ![]() , где
, где ![]() –
период ПСП сигнала (1),
–
период ПСП сигнала (1), ![]() ;
; ![]() – функциональный преобразователь с
характеристикой вида
– функциональный преобразователь с
характеристикой вида ![]() – тангенс гиперболический;
– тангенс гиперболический; ![]() и
и ![]() – выходные
величины синфазного и квадратурного каналов ФД соответственно.
– выходные
величины синфазного и квадратурного каналов ФД соответственно.

Рис. 1. Фазовый дискриминатор шумоподобного MSK-сигнала.
Оптимальный алгоритм фазового дискриминирования (2) шумоподобного MSK-сигнала имеет вид [3]:
|
|
(2) |
где ![]() – дисперсия аддитивного белого
гауссовского шума
– дисперсия аддитивного белого
гауссовского шума ![]() . Реализация алгоритма (2) на
основе программируемых логических интегральных схем (ПЛИС) затруднительна, в
связи с чем, актуальной является задача разработки квазиоптимального ФД с
минимальными потерями в помехоустойчивости.
. Реализация алгоритма (2) на
основе программируемых логических интегральных схем (ПЛИС) затруднительна, в
связи с чем, актуальной является задача разработки квазиоптимального ФД с
минимальными потерями в помехоустойчивости.
Упрощение оптимального алгоритма ФД (2) достигается путём
кусочно-линейной аппроксимации решающей функции ![]() :
:
В
качестве критерия, для сравнительного анализа помехоустойчивости алгоритмов (2)
и (3), используем дисперсию эквивалентных фазовых флуктуаций ![]() ,
, ![]() –
номер алгоритма ФД,
–
номер алгоритма ФД, ![]() – дисперсия выходной величины
дискриминатора при
– дисперсия выходной величины
дискриминатора при ![]() ,
, ![]() –
крутизна дискриминационных характеристик (черта сверху означает статистическое
усреднение) [2]. Выбор лучшего из квазиоптимальных алгоритмов ФД шумоподобного MSK-сигнала заключается в выборе параметра
–
крутизна дискриминационных характеристик (черта сверху означает статистическое
усреднение) [2]. Выбор лучшего из квазиоптимальных алгоритмов ФД шумоподобного MSK-сигнала заключается в выборе параметра ![]() в (3), обеспечивающего минимум функции
в (3), обеспечивающего минимум функции ![]() .
.
На рис. 2 представлены результаты статистического моделирования
(усреднение по ![]() испытаниям) квазиоптимального
алгоритма ФД при использовании аппроксимации (3) оптимальной решающей функции:
зависимость дисперсии
испытаниям) квазиоптимального
алгоритма ФД при использовании аппроксимации (3) оптимальной решающей функции:
зависимость дисперсии ![]() от крутизны аппроксимации
от крутизны аппроксимации ![]() при отношении «сигнал/шум» на входе
при отношении «сигнал/шум» на входе ![]() .
.
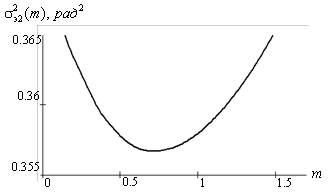
Рис. 2. Зависимость дисперсии эквивалентных фазовых флуктуаций от крутизны аппроксимации решающей функции.
Выводы.
1. Наилучший квазиоптимальный алгоритм фазового дискриминирования шумоподобного
MSK-сигнала может быть реализован на основе выражения
(3) при крутизне кусочно-линейной аппроксимации ![]() .
.
2. Предложенный алгоритм может быть реализован на основе ПЛИС фирмы Xilinx с использованием программного обеспечения MatLab-Simulink и Xilinx System Generator for DSP.
Работа выполнена при финансовой поддержке гранта, выделенного на выполнение поисковых научно-исследовательских работ в рамках федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009 – 2013 годы (Государственный контракт от 31.10.2011г. №16.740.11.0764).
Литература
1. Nard G. Geoloc spread spectrum concept applied in new accurate medium-long range radio positioning system. – France, Sercel – 03/89. – 23 p.
2. Жодзишский М.И. Цифровые системы фазовой синхронизации / М.И. Жодзишский, С.Ю. Сила-Новицкий, В.А. Прасолов и др. – Москва: «Советское радио», 1980. – 208 с.
3. Бондаренко В.Н. Помехоустойчивость алгоритмов фазового дискриминирования шумоподобного сигнала / В.Н. Бондаренко, Е.В. Кузьмин // Сб. науч. тр. «Соврем. пробл. радиоэл.». – М.: Радио и связь. – 2006. – С.53 – 56.
4. Бондаренко В.Н. Алгоритм автоподстройки по частоте для корабельной станции широкополосной радионавигационной системы / В.Н. Бондаренко, В.И. Кокорин, Е.В. Кузьмин // Навигация и гидрография. – 2007. – №24. – С.44 – 52.
5. Kuzmin E.V. Comparative Analysis of Phase-lock Control System Algorithms for Spread-spectrum Signal Receiver / Е.В. Кузьмин // Журнал Сибирского федерального университета. Серия «Техника и технологии». – Т.4. – №1. – 2011. – С.35 – 39.
Режим доступа: http://elib.sfu-kras.ru/bitstream/2311/2276/1/04_Kuzmin.pdf.