УДК 621.396.67

ПЛАНАРНЫЕ ЗЕРКАЛА НА ОСНОВЕ ПЕРИОДИЧЕСКИХ ОТРАЖАТЕЛЕЙ

С. Е. Банков ¹, М. Д. Дупленкова ²

¹ИРЭ им. В.А. Котельникова РАН, ²ОКБ МЭИ

Получена 22 января 2012 г.

Аннотация. Рассмотрены вопросы проектирования планарных зеркал для квазиоптических интегральных антенн миллиметрового диапазона на основе периодических отражателей. Исследуются отражатели, выполненные в виде двумерной или одномерной решетки щелей в экране плоского волновода. Вводятся показатели качества отражателей. Анализируются их зависимости от геометрических параметров структур. Обсуждаются технические характеристики планарных зеркал на основе периодических отражателей.

Ключевые слова: интегральная антенна миллиметрового диапазона, планарное зеркало, периодическая структура, электромагнитный кристалл.

Abstarct. Problems of design of planar mirrors for quasi – optical antennas of millimeter wave range on the base of periodical reflectors are considered. Reflectors in form of two and one dimensional arrays of slots in a screen of parallel plate waveguide are investigated. Quality factors of reflectors are introduced. Dependencies of quality factors on parameters of arrays are studied. Technical characteristics of planar mirrors on the base of periodical reflectors are discussed.

Keywords: integrated millimeter wave antenna, planar mirror, periodical structure, electromagnetic crystal.

1. Постановка задачи

Техническое освоение коротковолновой части миллиметрового и субмиллиметрового диапазонов (КЧ ММД и СММД) делает актуальной задачу поиска новых технологий построения экономичных СВЧ устройств указанных диапазонов. К их числу относятся антенны и антенные решетки. Достижение высокой технологичности в СВЧ технике традиционно связывают с использованием технологии печатных схем [1], которые обладают высокой повторяемостью, низкой стоимостью и т.д.

В технике дециметрового и сантиметрового диапазонов активно используются печатные антенны. Они могут выполнять функцию одиночного излучателя или объединяться в систему – антенную решетку (АР). Исследуемые в данной работе структуры могут использоваться при построении высоконаправленных печатных антенных решеток КЧ ММД и СММД.

Традиционно печатные АР содержат две важные части: излучающая решетка и схема ее возбуждения. В относительно низкочастотных диапазонах схемы возбуждения выполняются на основе печатных линий передачи: микрополосковых, полосковых, копланарных и т.д. С повышением частоты такие технические решения становятся неэффективными [2] вследствие роста тепловых потерь в указанных линиях передачи. Поэтому при переходе в ММД их заменили волноводы разных видов: металлические, диэлектрические, щелевые.

Дальнейшее продвижение в КЧ ММД может быть связано с отказом от волноводного способа построения схемы возбуждения АР и переходом к квазиоптическому способу возбуждения АР.

В последнее время появился ряд технических решений в данной области, в которых схемы возбуждения печатных АР строятся на основе таких квазиоптических элементов как зеркала и линзы. Здесь можно отметить многолучевую щелевую АР, которая возбуждается двухзеркальной оптической системой Кассегрена [3]. Ее зеркала выполнены в виде решеток металлических цилиндров, которые размещены внутри плоского волновода (ПВ). Поскольку оба зеркала и АР располагаются в одной плоскости, то используемая система Кассегрена выполнена из офсетных зеркал, позволяющих избежать эффекта затенения.

В работах [4] и [5] рассматриваются ленточные АР, которые возбуждаются линзовыми схемами. Роль планарной линзы выполняет область диэлектрической подложки, в которой на ее поверхностях размещаются ленточные периодические решетки. В указанных работах показано, что подложка с ленточными решетками может рассматриваться как среда с принудительным преломлением [6], которая позволяет проектировать широкоугольные линзовые системы.

В работе [7] рассматривается двухслойное планарное зеркало, которое используется для построения схемы возбуждения щелевой решетки на основе ПВ. Двухслойные зеркала выгодно отличаются от однослойных [3] отсутствием эффекта затенения, поскольку в них отражение от поверхности зеркала сопровождается одновременным переходом энергии отраженных волн с одного слоя на другой. Зеркало в работе [7] выполнено в виде сплошной металлической стенки, размещенной перпендикулярно ПВ.

Принципы построения двухслойных зеркал развиваются в работе [8], в которой отражающая поверхность выполнена в виде периодической структуры, которая находится в запрещенной зоне. Такие структуры в СВЧ диапазоне принято называть электромагнитными кристаллами (ЭМК) [9] по аналогии с фотонными кристаллами, которые используются в оптике [10]. ЭМК использованный в работе [8] представляет собой двумерную решетку из металлических цилиндров. Ее достоинством является то, что она может быть выполнена в рамках технологии печатных схем СВЧ. В этом случае цилиндры реализуются в виде металлизированных отверстий в печатной плате.

Следует отметить, что при повышении частоты и переходе в КЧ ММД и далее в СММД описанные выше способы создания планарных зеркал в виде металлизированных отверстий теряют свою эффективность. Указанная тенденция связана со сложностью изготовления большого числа отверстий, которые должны иметь весьма малый диаметр (порядка 1 – 2 десятых миллиметра) и расположены на малых расстояниях друг от друга. Кроме того, следует отметить рост тепловых потерь в таких структурах. Поэтому актуальной задачей, решению которой посвящена данная работа, является поиск новых конструкций планарных зеркал, которые могут быть изготовлены исключительно методами печатной технологии без использования металлизированных отверстий.

Отметим, что планарные волноводы представляют собой широкий класс направляющих структур, в плоскости которых могут распространяться электромагнитные волны разных типов. Частным случаем планарного волновода является ПВ, который работает на основной Т – волне. В данной работе мы ограничимся анализом зеркал, выполненных на основе ПВ. Такие зеркала должны эффективно отражать Т – волны.

Другим часто используемым в квазиоптических интегральных схемах типом волны является Н₁ – волна планарного диэлектрического волновода. Проблема создания эффективных и технологичных зеркал для таких волн также весьма актуальна. Однако она имеет простое решение, основанное на создании запредельных областей [5], которые обеспечивают практически полное отражение волн, поляризованных в плоскости планарного волновода.

Указанный способ построения зеркал для волн, поляризованных ортогонально плоскости ПВ, к которым относится Т – волна, неприменим, так как для них невозможно создать запредельные области с помощью металлических экранов. Данное обстоятельство объясняет наш выбор объекта исследования: ПВ с Т – волнами.

Прежде чем переходить к изложению содержания работы, сделаем еще одно важное замечание. На первый взгляд для создания эффективного и технологичного отражателя Т – волн ПВ следует использовать обрыв экранов, который был изучен в работе [11]. Действительно, на относительно низких частотах обрыв полосковых проводников является для Т – волн сильной нерегулярностью, которая близка по своим свойствам к нагрузке типа холостой ход. Излучение за пределы ПВ при этом весьма мало, а модуль коэффициента отражения Т – волны близок к единице. Под низкими частотами мы понимаем частоты, на которых высота ПВ много меньше длины волны в заполняющем его диэлектрике.

Однако, при повышении частоты выполнение ограничения на высоту ПВ становится весьма сложным. Пренебрежение им приводит к резкому росту эффекта преобразования Т – волны ПВ в Е₁ – волну диэлектрической подложки, которая уносит энергию за пределы ПВ. В результате модуль коэффициента отражения Т – волны уменьшается, что эквивалентно потерям мощности в планарном зеркале.

Указанные выше причины не позволяют использовать в качестве отражателя Т – волн ПВ обрыв его экранов и заставляют искать другие варианты решения поставленной задачи. Одним из них является применение щелевых периодических структур (см. рис. 1). Щели выполняются в одном или двух экранах ПВ. Нетрудно заметить, что их изготовление может быть выполнено исключительно методами печатной технологии.

Известно, что периодическая структура при определенных условиях может находиться в полосе запирания [12], в которой она является непрозрачной для электромагнитных волн. В этой полосе она практически полностью их отражает назад. Условия возникновения запрещенной зоны не связаны с высотой ПВ. Они определяются периодом структуры. Поэтому отражатели данного типа не требуют применения тонких подложек и могут использоваться на сравнительно высоких частотах.

Рис. 1. Отражатель на периодической структуре

Из рис. 1 видно, что мы будем исследовать отражатель с щелями бесконечной длины, которые образуют одномерную решетку.

2. Математическая модель отражателя, его показатели качества

Одномерная решетка на основе бесконечных щелей в экране ПВ рассматривалась в разных работах, например, в работе [13], в которой данная структура исследовалась в качестве антенны бегущей волны. С математической точки зрения, ее анализ как отражателя не имеет существенных отличий. Поэтому при численных расчетах мы использовали модель аналогичную модели описанной в [13]. Подробно ее описывать не имеет смысла. Мы приведем только ограничения, принятые в работе [13] существенные для нашего исследования.

Решение граничной задачи в работе [13] проводилось при следующих допущениях и ограничениях. Решетка была бесконечной по оси 0у и имела конечные размеры по оси 0х. Она возбуждалась основной Т – волной при ПВ при , которая падает на решетку под углом падения относительно оси 0х. Щели считались узкими. Ширина щели полагалась малой по сравнению с длиной волны . Высота ПВ ограничивалась половиной длины волны в среде с относительной диэлектрической проницаемостью , которая заполняет ПВ. При выполнении этого условия в ПВ может распространяться только основная Т – волна. Рассматривалась структура без тепловых потерь.

Исходная граничная задача сводилась к системе интегральных уравнений относительно магнитных токов в щелях. При этом регулярность структуры вдоль оси 0у позволяет зафиксировать зависимость поля от координаты , которая определяется падающей волной:

, (1)

где - волновое число свободного пространства, - относительная диэлектрическая проницаемость материала ПВ.

Отсутствие периодичности решетки вдоль оси 0х не позволяет простым образом связать магнитные токи в щелях, имеющих разные координаты . Поэтому задача сводится к системе интегральных уравнений порядка , где - число щелей в линейке.

Приближение узких щелей позволяет пренебречь поперечной компонентой магнитного тока и рассматривать только одну компоненту, направленную вдоль оси щели. Решение системы интегральных уравнений проводилось методом Галеркина. Неизвестные функции, описывающие магнитные токи в щелях представлялись в виде ряда по базисным функциям с неизвестными коэффициентами. В качестве базисных функций были взяты, часто используемые при анализе щелевых структур функции, учитывающие особенности токов на кромках щелей. Применение метода Галеркина сводит систему интегральных уравнений к системе алгебраических уравнений, которая решается численно.

После определения магнитных токов в щелях находятся внешние параметры решетки. К ним относятся: коэффициент отражения Т - волны от решетки , ее коэффициент прохождения , поля излучения. Для оценки исследуемых структур в качестве планарных зеркал нам необходимо ввести их показатели качества (ПК). Для этого рассмотрим ряд характеристик структуры выполненной на подложке с =2, которая имеет следующие геометрические размеры: h=8, P_x=10.4, w=4. Здесь и далее все размеры приводятся в миллиметрах. Угол падения во всех примерах данного раздела равен нулю.

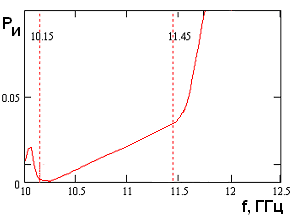
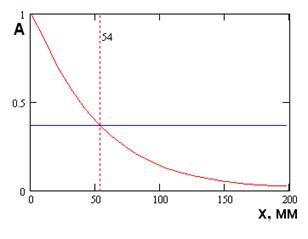
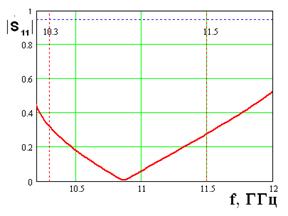
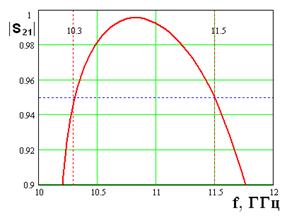
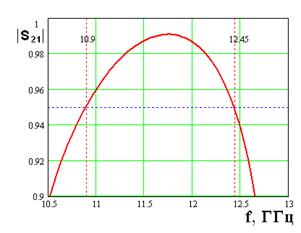
На рис. 2 – 4 приведены типичные зависимости ее внешних параметров. На рис. 2 показана частотная зависимость модуля коэффициента отражения Т – волны ПВ от решетки. На рис. 3 представлена частотная зависимость относительной мощности излучения в свободное пространство. На рис. 4 показано распределение нормированных амплитуд магнитных токов в щелях вдоль оси 0х. Амплитуды токов нормированы на амплитуду тока в первой по оси 0х щели.

Рис. 2. Частотная зависимость модуля коэффициента отражения

Рис. 3. Зависимость излученной мощности от частоты

Рис. 4. Зависимость нормированных амплитуд токов в щелях от расстояния вдоль оси 0х.

Рассматривая приведенные зависимости, отмечаем, что модуль коэффициента отражения близок к единице в пределах некоторой полосы частот, которая является полосой запирания периодической структуры. Зададим минимальный уровень модуля коэффициента отражения равным 0.95. Будем использовать его для определения минимальной и максимальной частот рабочего диапазона отражателя, а также для определения его ширины Δf, которая в данном случае составляет 1.65 ГГц (см. рис. 3.1), центральная частота рабочего диапазона f₀ равна 11 ГГц.

Стандартное определение ПК [14] требует, чтобы ПК монотонно уменьшался при улучшении качества устройства. С практической точки зрения нам желательно иметь максимальную ширину рабочего диапазона . Однако, использование параметра как ПК вступает в противоречие с указанной работой [14]. Поэтому будем для оценки полосовых свойств отражателя использовать эквивалентную добротность :

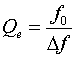. (2)

Нетрудно увидеть, что эквивалентная добротность уменьшается при улучшении качества отражателя.

Зависимость относительной излученной мощности от частоты показана на рис. 3. Этот параметр определяется следующим образом:

. (3)

Относительная излученная мощность Р_и в полосе частот меняется от 0.001 на нижней границе полосы, до 0.035 на верхней границе (см. рис. 3). На центральной частоте f₀ излученная мощность примерно составляет 0.0175. Величина Р_ихарактеризует потери мощности на излучение в исследуемой структуре. В качестве ПК мы возьмем ее значение на центральной частоте рабочего диапазона.

При проектировании отражателя на периодической структуре важным вопросом является выбор числа щелей вдоль оси 0х . Для решения данного вопроса необходимо проанализировать зависимость нормированных амплитуд магнитных токов на щелях от расстояния вдоль оси 0х, показанную на рис. 3. Видно, что амплитуды убывают по закону близкому к экспоненциальному. Число щелей должно быть таким, чтобы магнитный ток на последней щели был пренебрежимо мал. Размеры решетки по оси 0х удобно характеризовать параметром, который условно можно назвать толщиной скин-слоя t (см. рис. 4). На длине магнитные токи затухают в раз. В данном случае на центральной частоте она равна 54. Будем использовать толщину скин – слоя в качестве еще одного ПК, описывающего отражатель.

Поскольку рассматриваемые структуры мы предполагаем использовать для построения планарных зеркал, то нам необходимо учитывать, что на поверхность зеркала падают лучи с разными углами падения. Поэтому зеркало должно сохранять свою работоспособность в некотором диапазоне углов падения.

Увеличение угла падения относительно его нулевого значения приводит к увеличению центральной частоты рабочего диапазона. В результате полная полоса рабочих частот, в которой отражатель сохраняет работоспособность в диапазоне углов падения уменьшается. Для оценки величины смещения полосы рабочих частот выделим на рис. 2 характерную точку, в которой коэффициент отражения достигает максимума. Практически он равен по модулю единице на данной частоте . Численные расчеты показали, что с хорошей точностью частота определяется следующим простым соотношением:

, (4)

где - угол падения Т – волны, а период берется в миллиметрах. Частота весьма близка к верхней границе полосы запирания периодической структуры.

Если при изменении угла падения ширина полосы запирания меняется незначительно, то соотношение (4) можно также использовать для оценки смещения центральной частоты . На самом деле параметр немного увеличивается с ростом , компенсируя влияние смещения рабочего диапазона. Численные расчеты показали, что при углах падения меньших 15⁰ их влияние на ПК отражателя незначительно и достаточно оценить их при . Ограничение на углы падения приводит к ограничению на параметры планарных зеркал, которые должны иметь достаточно большое отношение фокусного расстояния к размеру зеркала . Таким образом, результаты дальнейшего анализа будут справедливы только для длиннофокусных зеркал. Например, в случае параболического зеркала отношение должно быть больше 1.15.

3. Численные результаты для решетки с бесконечными щелями

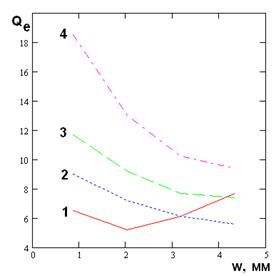
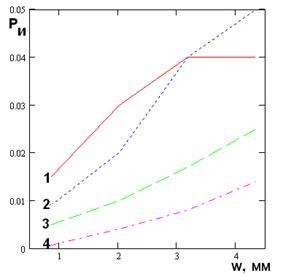
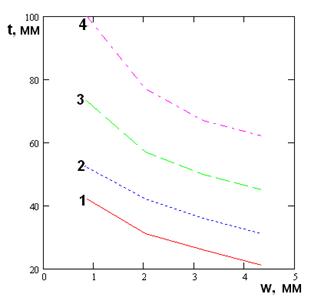
В данном разделе рассмотрим численные результаты, полученные при анализе структуры с бесконечными щелями. Рассмотрим, как ее геометрические размеры влияют на ПК, к которым относятся эквивалентная добротность Q_e, относительная излученная мощность Р_и, толщина скин-слоя t. Изменяя высоту ПВ h в диапазоне 4.5 - 8.5 мм и ширину щелей w от 0.9 до 4.3, при фиксированном размере P_x=10.4 получаем графики, показанные на рис. 5 - 7 ( кривые 1 – 4 соответствуют h=4.5, 5.9, 7.3, 8.7).

Рис. 5. Зависимость добротности от ширины щели при ε=2

Рис. 6. Зависимость излученной мощности от ширины щели при =2

Рис. 7. Зависимость толщины скин-слоя от ширины щели

при =2

Анализируя полученные графики, отмечаем, что в случае относительно тонкой подложки h=4.5 при w>2, монотонность зависимостей на рис. 5, 6 нарушается. Это связано с особенностями частотной зависимости модуля коэффициента отражения. Из рис. 2 видно, что в полосе запирания коэффициент отражения сначала резко растет почти до единицы, а затем медленно уменьшается по закону близкому к линейному. Относительно медленное его уменьшение сменяется резким падением, которое соответствует границе полосы запирания. Медленное изменение коэффициента отражения в полосе запирания связано с ростом излученной мощности.

Если выбранный нами минимально допустимый уровень коэффициента отражения попадает на участки его резкого изменения, как показано на рис. 2, то при этом ПК решетки меняются монотонно (см. кривые 2 – 4 на рис. 5,6). Однако, если предельный уровень коэффициента отражения пересекает кривую его частотной зависимости на участке медленного изменения, как показано на рис. 8, то эквивалентная добротность решетки и излученная мощность начинают быстро и немонотонно меняться при изменении параметров структуры.

Рис. 8. Частотная зависимость модуля коэффициента отражения

для решетки с размерами h=4.5, P_x=10.4, w=3.5

Периодическая решетка бесконечных щелей при фиксированной центральной частоте рабочего диапазона имеет два свободных геометрических размера: толщину ПВ h и ширину щели w, так как период решетки P_x связан с указанной частотой соотношением (4). В связи с этим оказывается возможным провести двумерную аппроксимацию зависимостей ПК решетки от ее параметров в ограниченной области изменения значений параметров h и w. Такая двумерная сплайн аппроксимация была выполнена в среде Маткад для структур с диэлектрической проницаемостью 2,4,6,8,10. Параметры решетки менялись в следующих пределах:

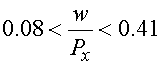(5)

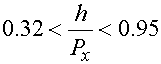
Период решетки P_x выбирался из условия =10 ГГц. Отметим, что полученные для конкретного значения центральной частоты результаты могут быть использованы также для других частот в силу принципа электродинамического подобия путем пропорционального длине волны изменения геометрических размеров.

Для построения сплайн аппроксимации использовалось дискретное множество значений параметров h и w. Число узловых точек для каждого значения диэлектрической проницаемости было выбрано равным шестнадцати.

Построенная аппроксимационная модель позволяет проводить расчет значений ПК в промежуточных точках, а также оптимизацию исследуемой структуры без существенных затрат компьютерных ресурсов в отличие от модели основанной на решении электродинамической задачи.

На рис. 9 показана зависимость эквивалентной добротности от высоты ПВ, полученная с помощью сплайн аппроксимации для . Кривая 1 получена для w=1.2, а кривая 2 для w=4.

Рис. 9. Зависимость эквивалентной добротности от высоты ПВ, полученная в результате двумерной аппроксимации для =2

Оценить точность аппроксимационной модели можно с помощью табл. 1, в которой представлены значения ПК решетки, полученные путем электродинамических расчетов и с помощью приближенной модели.

Таблица 1.

Параметры решетки	Интерполяция	Точный расчет
h=5, w=1.2	=7 Р_и=0.015 t=40	=6.8 Р_и=0.017 t=39
h=6.5, w=2.5	=7.3 Р_и=0.02 t=45	=7.2 Р_и=0.018 t=44
h=8, w=4	=8.5 Р_и=0.013 t=55	=8.3 Р_и=0.015 t=54

4. Выбор оптимальных параметров

Из рис. 5 – 7 видно, что изменение параметров отражатели улучшает одни ПК и ухудшает другие. Такое поведение ПК соответствует наличию технического противоречия, которое препятствует одновременному улучшению всех ПК.

Теория оценки технических объектов по совокупности ПК [14] рекомендует проводить оценку устройства и выбор оптимальных параметров в пространстве ПК. Для этого нам необходимо построить зависимости одних ПК от других. Например, мы можем анализировать зависимости эквивалентной добротности и толщины скин – слоя от излученной мощности . Для этого с помощью аппроксимационной модели мы можем провести расчет зависимостей , и от высоты ПВ при постоянной ширине щели и затем построить зависимости и , исключая тем самым параметр . При этом мы получим семейство кривых, каждая из которых соответствует фиксированному значению .

На рис. 10 и 11 показаны указанные выше зависимости, полученные для . Кривые 1 – 5 соответствуют . Высота ПВ менялась в пределах от 3.7 до 6.1.

В силу принятых выше определений ПК они монотонно уменьшаются при улучшении исследуемого устройства. Поэтому лучшее устройство соответствует точкам на кривых 1 – 5, расположенным ближе к началу координат.

Рис. 10. Зависимость эквивалентной добротности от мощности излучения

Рис. 11. Зависимость толщины скин – слоя от мощности излучения

Протяженность каждой из кривых 1 – 5 определяется диапазоном изменения высоты ПВ. При этом верхняя левая граница кривой соответствует максимальному значению , а правая нижняя минимальному . На практике всегда диапазон изменения любого параметра ограничен разными факторами, например возможностью его реализации. В случае высоты ПВ сверху она ограничена условиями одноволнового режима ПВ, а снизу технологическими возможностями созданию тонких подложек. Другим фактором, определяющим может быть затухание Т – волны ПВ, которое растет с уменьшением его высоты.

Диапазон изменения ширины щели также ограничен. Минимальная ширина щели чаще всего определяется технологическими возможностями. Максимальное ее значение не может быть больше периода .

Из рис. 10 и 11 видно, что при отсутствии ограничений на высоту ПВ ближе всего к началу координат лежит кривая 1, соответствующая минимальной ширине щели . Поэтому в этом случае выбор параметра был бы очевидным: необходимо принять . При наличии ограничений на параметр выбор параметров структуры видоизменяется.

Он поясняется зависимостью ПК, показанной на рис. 12. Кривая на рис. 12 соответствует оптимальным значениям ПК и . Она получена следующим образом.

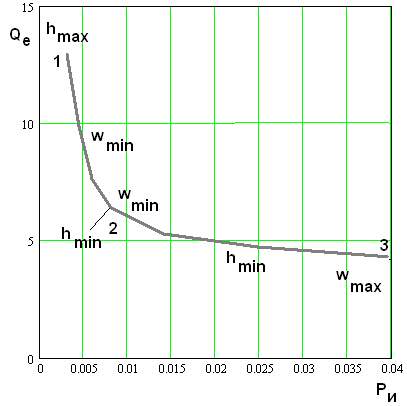
Рис. 12. Зависимость оптимальных значений ПК

На участке 1 – 2 кривая на рис. 12 совпадает с кривой 1 на рис. 10. На этом участке , . Участок кривой 2 – 3 получен путем соединения крайних нижних точек кривых 1 – 5 на рис. 10, поскольку при наличии ограничений они безусловно лучше других точек на указанных кривых. На данном участке , .

Аналогично может быть получена зависимость оптимальных значений ПК от . Она показана на рис. 13.

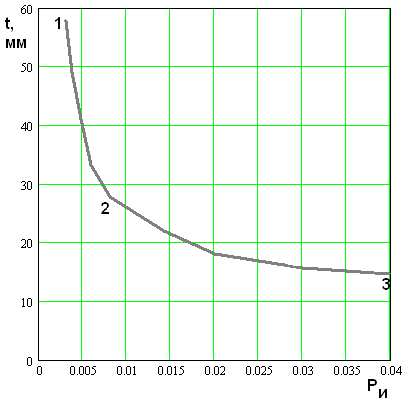
Рис. 13. Зависимость оптимальных значений ПК

Точки 1 – 3 имеют тот же смысл, что и на рис. 12. Кривые на рис. 12 и 13 представляют наилучшие из возможных значений ПК отражателя при . На рис. 14 показаны зависимость оптимальных значений параметров структуры от излученной мощности. Точки 1 – 3 на рис. 14 соответствуют точкам 1 – 3 на рис. 12 и 13.

Из рис. 12 и 13 видно, что мы получили не одно оптимальное техническое решение, а множество решений (отражателей). Каждой точке этого множества соответствует свой набор ПК, которые можно определить с помощью кривых на указанных рис. 12 и 13. С помощью кривых на рис. 14 мы можем найти значения параметров, которые реализуют выделенную совокупность ПК.

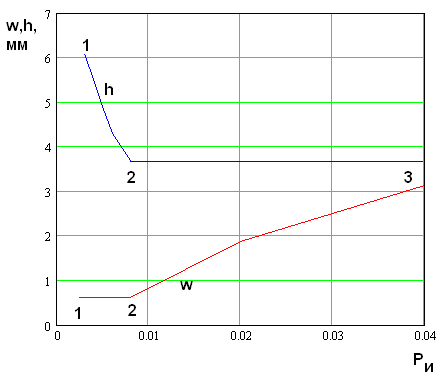
Рис. 14. Зависимость оптимальных значений параметров от излученной мощности

Отметим, что результат оптимизации в виде множества оптимальных решений является естественным следствием использования множества ПК для оценки нашего устройства [14]. Полученное выше множество оптимальных решений в теории оптимизации по совокупности ПК получило название множества нехудших решений (МНХ) [14].

Рассмотрим далее зависимость ПК и друг от друга. Пример такой зависимости для показан на рис. 15. Видно, что эти ПК не находятся в противоречии друг с другом. В принципе, если не обращать внимание на увеличение их можно улучшать одновременно.

Рассмотрим далее МНХ, полученные с помощью процедуры, описанной выше для других значений диэлектрической проницаемости .

Рис. 15. Зависимость оптимальных значений ПК от

На рис. 16 показаны кривые зависимости оптимальных значений ПК от . Кривые 1 – 4 получены для 2,4,6,10. Из рис. 16 видно, что с увеличением диэлектрической проницаемости ПВ соответствующая кривая смещается к началу координат. Отсюда мы можем сделать вывод о том, что наилучший вариант соответствует максимально допустимому значению .

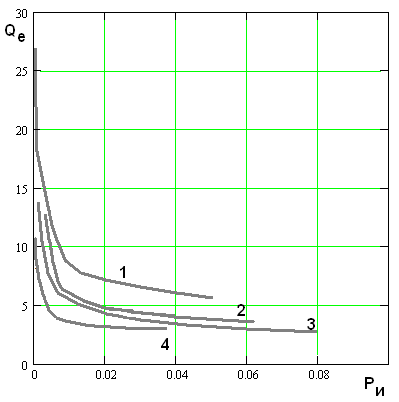
Рис. 16. Зависимость оптимальных значений ПК для разных значений диэлектрической проницаемости

5. Двухслойное зеркало на основе решетки из бесконечных щелей

Конструкция двухслойного зеркала показана на рис. 17. Оно состоит из следующих элементов: ПВ 1 и 2, межслойного перехода 3, щелевой решетки 4, выполненной методами фотолитографии на металлизированной пленке и возбуждающего элемента 5. Рассмотрим принципы функционирования элементов зеркала. ПВ 1 возбуждается источником 5. Возникающая в нем волна доходит до межслойного перехода 3 претерпевает там два преобразования. Первое: она отражается от решетки бесконечных щелей 4 назад, второе: она переходит с нижнего слоя 1 на верхний слой 2.

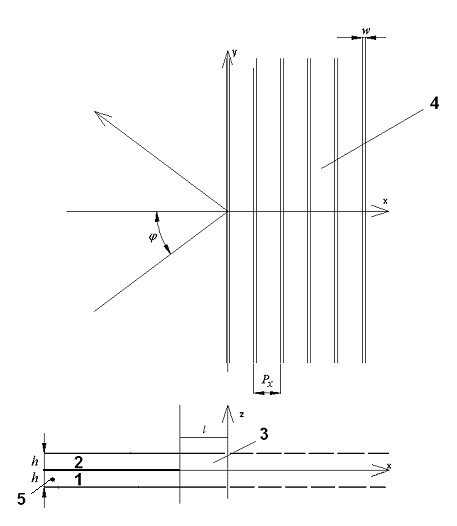
Рис. 17. Конструкция двухслойного зеркала

Наиболее сложным элементом зеркала за исключением собственно решетки является межслойный переход 3. Структура бесконечна по оси 0y и может возбуждаться собственными волнами ПВ со стороны входов 1 и 2, набегающими на структуру под произвольными углами j. Математическая модель межслойного перехода была рассмотрена в [6]. Межслойный переход симметричен относительно плоскости YOZ. Поэтому его можно анализировать независимо для случаев четного и нечетного возбуждения, размещая в плоскости симметрии последовательно электрическую и магнитную стенки [15]. В обоих случаях мы имеем дело с парциальными четырехполюсниками, которые характеризуются коэффициентами отражения и прохождения. Для четного возбуждения это коэффициент отражения S_11ч, а для нечетного - S_11н. При нечетном возбуждении (электрическая стенка в плоскости симметрии) структура парциального четырехполюсника – это отрезок волновода длиной l, к которому присоединяется решетка бесконечных щелей, матрица рассеяния которой определена в разделе 3. Тогда найти матрицу рассеяния парциального четырехполюсника не составляет труда:

, , (6)
где k –волновое число среды, заполняющей плоские волноводы, а - угол падения волны, R – коэффициент отражения решетки бесконечных щелей.

В случае четного возбуждения парциальный четырехполюсник имеет более сложную структуру, показанную на рис. 18. Верхняя стенка плоского волновода на участке 1 – идеально проводящая стенка, а на участке 2 – это идеальная магнитная стенка.

Рис. 18. Четное возбуждение парциального четырехполюсника

В работе [6] рассматривалась задача возбуждения четырехполюсника аналогичного показанному на рис. 18. Его отличие состояло в том, что вместо решетки при располагалась идеально проводящая вертикальная стенка с коэффициентом отражения равным минус единице. В упомянутой работе было показано, что межслойный переход может функционировать в двух разных режимах: статическом и динамическом. Статический режим реализуется при выполнении неравенства:

. (7)

Если неравенство (7) удовлетворяется, то волновод на участке оказывается запредельным. Распространяющиеся типы волн в нем отсутствуют. Во многих практически важных случаях запредельные волны на участке затухают настолько, что влиянием нерегулярности при можно пренебречь. Тогда коэффициент отражения от парциального четырехполюсника можно приближенно считать равным коэффициенту отражения от скачка граничных условий в точке , в которой при соединяются электрическая и магнитная стенки. Анализ такой структуры выполнен, например, в работе[16]. Полученное в ней выражение для коэффициента отражения мы можем использовать в качестве параметра S_11ч.

Если неравенство (7) не выполняется, то в волноводе при распространяется, по крайней мере, одна волна. Наличие распространяющихся волн меняет характер функционирования устройства и переводит его в динамический режим. В работе [6] показано, что со многих точек зрения статический режим предпочтительнее динамического. Поэтому мы ограничились оценкой параметров двухслойного зеркала с решетчатым отражателем только в статическом режиме.

Считая, что коэффициенты отражения от парциальных четырехполюсников известны, получим выражения для матрицы рассеяния зеркала в целом. Для этого следует воспользоваться методом симметрии [15]:

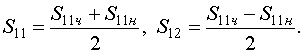
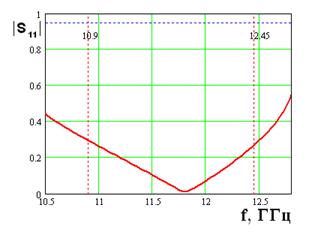
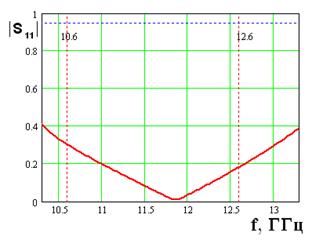
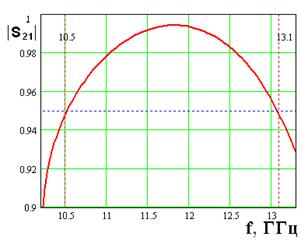
На рис. 19 - 22 (а, б) представлены частотные зависимости коэффициентов отражения и прохождения от двухслойного зеркала при нормальном падении волны, структура выполнена на подложке с диэлектрической проницаемостью соответственно =2, 4, 6, 10. Зависимости, представленные на рис. 19 а, б, соответствуют зеркалу со следующими геометрическими параметрами: h=4.5, P_x=10.4, w=2, l=3.5, =2. Такое зеркало имеет полосу пропускания 1.2 ГГц. Зависимости, представленные на рис. 20 а, б, соответствуют зеркалу со следующими геометрическими параметрами: h=3.7, P_x=7.35, w=2.5, l=2, =4. Такое зеркало имеет полосу пропускания 1.55 ГГц. Зависимости, представленные на рис. 21 а, б, соответствуют зеркалу со следующими геометрическими параметрами: h=2.6, P_x=6, w=2.5, l=2, =6. Такое зеркало имеет полосу пропускания 2.3 ГГц. Зависимости, представленные на рис. 22 а, б, соответствуют зеркалу со следующими геометрическими параметрами: h=2, P_x=4.65, w=2, l=1.6, =10. Такое зеркало имеет полосу пропускания 2.6 ГГц. Из рисунков видно, что при правильном выборе параметров перехода возможно хорошее согласование в достаточно широком диапазоне частот, при увеличении диэлектрической проницаемости полоса пропускания увеличивается.

(а)

(б)

Рис. 19. Частотные характеристики зеркала при =2

(а)

(б)

Рис. 20. Частотные характеристики зеркала при =4

(а)

(б)

Рис. 21. Частотные характеристики зеркала при =6

(а)

(б)

Рис. 22. Частотные характеристики зеркала при =10

Отметим в заключение, что все представленные численные примеры выполнены для конкретного диапазона частот близких к 10 ГГц. Численные результаты могут быть без труда использованы для оценки двухслойного зеркала на других частотах в силу принципа электродинамического подобия.

Данная работа выполнена при поддержке Российского фонда фундаментальных исследований, проект № 12-08-12003-офи_м.

Литература

Взятышев В.Ф., Нарытник Т.Н., Рябов Б.А., Емельяненков Б.Н., Банков С.Е. // Обзоры по электронной технике. - М.: ЦНИИ “Электроника”, 1985, Вып. 13, 62 с.
Взятышев В.Ф. Диэлектрические волноводы. М.: Сов. Радио. 1970.
M. Ettorre, S. Bruni, G. Gerini, A. Neto, N. Llombart, S. Maci, Sector PCS-EBG Antenna for Low Cost High Directivity Applications, Antennas and Wireless Propagation Letters, Vol.6, pp. 537-539, Dec. 2007.
Bankov S.E., Douplenkova M.D., Kalinichev V.I., Kozin V.N., Levchenko I.V., Kuranov U.V., Rodionova E.V., Vasjukov V.D. 60 GHz Sensors Based on Dielectric Slotted Waveguide // 22nd European Microwave Conf. Proc. of Workshop “Commercial Applications of Microwave and Millimeter Waves”, 1992, p.p. 41-46.
Банков С.Е. Щелевые интегральные схемы миллиметрового диапазона // РЭ. 2006, Т. 51, №9, С. 1066-1086.
Корнблит С. СВЧ оптика. М.: «Связь». 1980.
С.Е. Банков. Проектирование и экспериментальное исследование решетки щелевых излучателей. // РЭ, 2004, т.49, №6, с. 701-706.
Банков С.Е., Весник М.В. Квазиоптический возбудитель антенной решетки на основе EBG структуры // РЭ. 2009. Т. 54. № 11, С. 1256-1266.
Банков С.Е. Электромагнитные кристаллы. М.: Физматлит. 2010.
Mosallaei H., Rahmat-Samii Y. // IEEE Trans. 2003. V. AP-51. №3. P. 549.
Нефедов Е.И., Фиалковский А.Т. Полосковые линии передачи. М.: Наука. 1980.
Силин Р.А. Периодические волноводы. М.: ФАЗИС. 2002.
Kalinichev V.I. // IEICE Trans. On Electronics, 1995, v. Et8-C, №10, p. 1447.
Гуткин Л.С. Оптимизация радиоэлектронных устройств по совокупности показателей качества. М.: Сов. радио, 1975.
Сазонов Д.М. Антенны и устройства СВЧ. М.: Высш. школа. 1988.
Левин Л. Теория волноводов. М.: Мир, 1978.

УДК 621.396.67

1 ИРЭ им. В.А. Котельникова РАН, 2 ОКБ МЭИ

¹ИРЭ им. В.А. Котельникова РАН, ²ОКБ МЭИ