УДК 621.396, 621.391
АНАЛИЗ ОБНАРУЖИТЕЛЯ LOG-CFAR С ЦИФРОВЫМ АДАПТИВНЫМ ПОРОГОМ ОБНАРУЖЕНИЯ НА ФОНЕ МОРСКИХ ПОМЕХ
И. Е. Чухломин, Н. А. Файзулин
Научно-исследовательский институт по измерительной технике – радиотехнические комплексы, г. Челябинск
Статья получена 10 ноября 2014 г., после доработки – 30 января 2015 г.
Аннотация. Исследуются два вида помех, воздействующие на приемный тракт амплитудного детектора и обнаружителя log-CFAR следящей импульсной РЛС, работающей по целеуказанию. Анализируются характеристики обнаружения воздушных целей на фоне помех, описываемых логнормальным и Рэлеевским законом распределения. Исследовано влияние добавочной константы логарифмической входной функции обнаружителя log-CFAR, на характеристики обнаружения.
Ключевые слова: морские помехи, обнаружитель CFAR, негауссовские помехи, распределение Рэлея, логнормальное распределение.
Abstract. The research deals with different types of sea clutter effecting the receiver path of amplitude detector and log-CFAR detector of pulse radar. Analysis is made for the performance aerial target detection through sea clutter described by lognormal and Rayleigh law of distribution. A study is conducted for influence of time constant for logarithmic input function displacement of log-CFAR detector on detection performance.
Keywords: sea clutter, CFAR detector, Rayleigh distribution, non-Gaussian clutter, lognormal distribution.
1. Введение
Радиолокационные станции (РЛС), работающие вблизи морской поверхности, неизбежно сталкиваются с отражением радиолокационных сигналов не только от объектов, подлежащих обнаружению, но и от самой морской поверхности, а также плохих метеоусловий (дождь, облачность, туман и.т.д.). Отражение радиосигнала от морской поверхности и плохих метеоусловий приводит к помехам различной природы и, следовательно, ухудшению характеристик обнаружения [2].
Функцию обнаружения полезного радиосигнала на фоне морских помех выполняет обнаружитель, который устанавливается непосредственно после амплитудного детектора.
В зарубежной литературе [1, 3, 5] рассматриваются несколько схем реализации обнаружителя, работающего при морских помехах, описываемых различными известными законами распределениями: логнормальным, Вейбула и k-распределением. Общей особенностью данных схем обнаружителей является использование логарифмической функции на входе обнаружителя, а также цифровое скользящее окно с набором специальных арифметических функций, с помощью которых вычисляется параметр распределения помехи σ. С помощью вычисления параметра σ обнаружитель приобретает свойство параметрического или другими словами становится адаптивным.
Экспериментальным исследованием закона распределения морских помех занимались японские ученые [1], с помощью надводной импульсной РЛС «Tokimec BR-3440MA-S314», технические характеристики которой по описанию [1] приведены в таблице 1.
Таблица 1.
|
Несущая частота, ГГц |
3,05 |
|
Мощность передатчика, кВт |
30 |
|
Длительность зондирующего импульса, мкс |
0,5 |
|
Частота следования зондирующих импульсов, Гц |
1600 |
|
Частота вращения антенны, об/мин |
22 |
|
Характеристика диаграммы направленности антенны в горизонтальной плоскости, ° |
1,8 |
|
Характеристика диаграммы направленности антенны в вертикальной плоскости, ° |
25 |
|
Поляризация |
Вертикальная |
|
Промежуточная частота приемника, МГц |
60 |
|
Полоса пропускания полосового фильтра, МГц |
5 |
В результате исследования было выявлено, что реальный закон распределения морских помех имеет схожую плотность вероятности с логнормальным и законом Вейбула (рис. 1), причем динамический диапазон данных распределений укладывается в 8 разрядов АЦП.
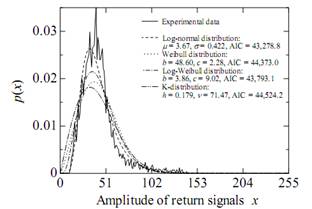
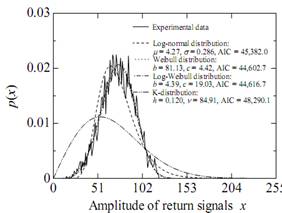

Рис. 1. Графики распределения плотностей вероятности
В данной статье, основываясь на результаты работы [1], морские помехи описываются логнормальным законом распределения, а шумы во входных цепях приемника Гауссовским законом распределения, которые преобразуются после амплитудного детектора в Рэлеевский закон распределения.
Функцию обнаружения полезного радиосигнала на фоне морских помех выполняет известная схема обнаружителя log-CFAR [1, 3, 5, 6] работающая по критерию Неймана-Пирсона.
Одной из основных проблем в импульсной РЛС, работающей вблизи водной поверхности, являются переходные процессы, связанные с непостоянством метеоусловий (частичная облачность и.т.д.), поэтому возникает необходимость в создании адаптивного обнаружителя способного работать при любых погодных условиях.
2. Обнаружитель log-CFAR
Структурная схема обнаружителя log-CFAR (от англ. constant false alarm rate – постоянный уровень ложных тревог) изображена на рис. 2.

Рис. 2. Структурная схема обнаружителя log-CFAR
x – входной цифровой сигнал, с
периодом дискретизации T; y – входной сигнал поступающий после
логарифмической функции; Log – функция
логарифма; Анти-log – функция обратная логарифму
(экспонента); ( )2 – математическая операция возведения в квадрат;
1/N – математическая операция вычисления
среднего значения; V(y) = σ2 – дисперсия
помехи; ![]() - математическая операция вычисления
квадратного корня; <y>
- среднее значение входного сигнала; z – нормированный выходной сигнал; Th – порог.
- математическая операция вычисления
квадратного корня; <y>
- среднее значение входного сигнала; z – нормированный выходной сигнал; Th – порог.
2.1 Характеристики обнаружителя log-CFAR при логнормальном распределении морской помехи
Пусть на вход обнаружителя log-CFAR поступают морские помехи, описываемые статистикой логнормального закона распределения. Плотность распределения вероятности логнормального закона:
 (1)
(1)
где x – входной сигнал, представляющий собой огибающую радиолокационных отражений; σ – среднеквадратическое отклонение; μ – математическое ожидание.
Для логнормального закона распределения помехи (1) сигналы в характерных точках схемы (рис. 2) имеют вид:
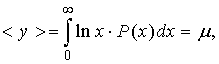
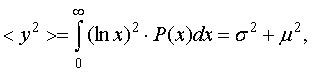 (2)
(2)
![]()
Закон распределения величины z имеет вид:
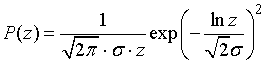 .
(3)
.
(3)
Вероятность ложных тревог обнаружителя log-CFAR:
 ,
(4)
,
(4)
где Th – порог; erf( ) – функция ошибки.
Если порог обнаружителя представить в виде:
то
![]() .
.
где b – табличное значение, при котором обеспечивается значение вероятности ложных тревог FL = 10-2; FL = 10-3 для логнормального закона распределения помехи (таблица 2).
Вероятность ложных тревог с учетом значений b будет определяться выражением:
![]() (6)
(6)
В соответствии с формулой (6) получим:
![]() .
.
Таблица 2.
|
FL |
Erf(b) |
b |
|
10-2 |
0,98 |
1,65 |
|
10-3 |
0,998 |
2,1 |
Таким образом, обеспечивается стабилизация величины F путем изменения порога Th, в соответствии с (5).
Вероятность правильного обнаружения цели:
 (7)
(7)
где S – амплитуда сигнала цели; Φ( ) – интеграл вероятности.
2.2 Характеристики обнаружителя log-CFAR при Рэлеевском распределении помехи
При отсутствии морских помех, помехи на входе будут создаваться за счет влияния входных цепей приемника. Данные помехи имеют стационарный характер распределения, подчиняющегося Гауссовскому закону, но поскольку на вход обнаружителя поступает сигнал, прошедший через амплитудный детектор, то помехи будут подчиняться Рэлеевскому закону распределения.
Плотность вероятности Рэлеевского закона распределения помехи [2, 5, 6, 7]:
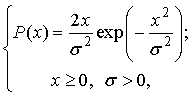 (8)
(8)
Сигналы в характерных точках схемы (рис. 2) имеют вид:
 ,
(9)
,
(9)
![]() ,
,
где γ – постоянная Эйлера равная 0,5772…[5].
Закон распределения величины z имеет вид:
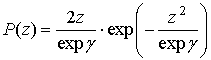 ,
(10)
,
(10)
Вероятность ложных тревог определяется выражением:
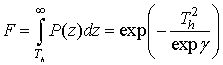 .
(11)
.
(11)
Для Рэлеевского распределения помехи в соответствие с формулой (5) и (9) получим:
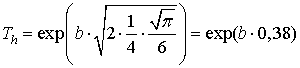 .
(12)
.
(12)
Тогда исходя из выражения (11) значение FR равно:
 .
(13)
.
(13)
Рассчитаем величины FR для значений b из таблицы 2. Расчетные данные FR изображены в таблице 3.
Таблица 3.
|
b |
0,76b-γ |
exp(0,76b-γ) |
FR |
|
1,65 |
0,667 |
1,96 |
0,145 |
|
2,1 |
1,019 |
2,77 |
0,062 |
Сравним вероятность ложных тревог FR и FL при различных величинах b (см. таблицу 4).
Таблица 4.
|
b |
|
|
1,65 |
14 |
|
2,1 |
62 |
По данным таблицы 4 можно сделать вывод, что при изменении закона распределения помехи с логнормального на Рэлеевский вероятность ложных тревог может увеличиваться почти на два порядка.
Вероятность правильного обнаружения цели при Рэлеевском распределении помехи [5]:
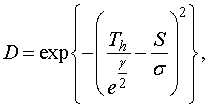 (14)
(14)
где D – вероятность правильного обнаружения цели; Th – порог; σ – среднеквадратическое отклонение случайной величины; S – амплитуда сигнала цели.
Реализация порога обнаружителя log-CFAR отдельно для логнормального и отдельно для Рэлеевского закона распределения помехи, является проблемной задачей. Стандартным решением данной проблемы, это использование карты помех, имеющую определенную сложность в практической реализации [4].
2.3 Принцип работы модифицированного обнаружителя log-CFAR
Рассмотрим принцип работы модифицированного обнаружителя log-CFAR при введении добавочной константы k перед функцией логарифма (рис. 3). Отличительной особенностью модифицированного обнаружителя log-CFAR от обычного (Рис. 2), является отвод цифрового скользящего окна не с середины, а с начала отсчета данных. Порог модифицированного обнаружителя log-CFAR реализован с запоминанием порога до следующего зондирования (строба).

Рис. 3. Структурная схема модифицированного обнаружителя
log-CFAR с добавочной константой
В связи с трудностью вычисления вероятности ложных тревог F и вероятности правильного обнаружения цели D при y = ln(x+k), проведено имитационное моделирование.
3. Моделирование модифицированного обнаружителя log-CFAR
Моделирование обнаружителя log-CFAR проводилось в пакете программ MATLAB. Блок-схема модели обнаружителя log-CFAR изображена на рис. 4.
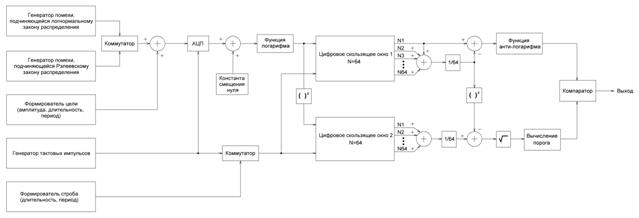
Рис. 4. Блок-схема модели обнаружителя log-CFAR
Моделирование системы обнаружителя log-CFAR производилось при параметрах указанных в таблице 5.
Таблица 5. Параметры модели обнаружителя log-CFAR
|
Период тактовых импульсов |
0,15 мкс |
|
Длительность цели |
0,2 мкс |
|
Длительность строба (зондирования) |
9,6 мкс |
|
Разрядность АЦП |
10 бит |
|
Размер цифрового скользящего окна |
64 |
|
Логнормальный закон распределения имеет следующие характеристики: 1. μ=3,67; σ=0,422, 2. μ=4,27; σ=0,286, 3. μ=4,13; σ=0,321. |
|
|
Рэлеевский закон распределения имеет следующие характеристики: 1. σ=10, 2. σ=20, 3. σ=30. |
|
|
Вероятность ложных тревог составляет: 1. F=10-2, 2. F=10-3. |
|
|
Вероятность правильного обнаружения цели: 1. D=0,5, 2. D=0,9. |
|
|
Величина добавочной константы: 1. k=1, 2. k=5, 3. k=10, 4. k=20. |
|
Значения F и D выбраны, исходя из того, что обнаружитель log-CFAR предназначен для обнаружения единичных зондирующих импульсов.
Различные плотности вероятности распределения помехи логнормального и Рэлеевского закона изображены на рис. 1 и рис. 5.

Рис. 5. Графики плотности вероятности Рэлеевского закона
Вычисление порога у обнаружителя log-CFAR производилось согласно формуле (5) для логнормального и Рэлеевского закона распределения помехи.
3.1. Моделирование стабилизации ложных тревог обнаружителя log-CFAR при Рэлеевском и логнормальном законе распределения помехи
Моделирование стабилизации частоты ложных тревог обнаружителя log-CFAR проводилось при вероятности ложных тревог F=10-2 и F=10-3, и различных значениях добавочной константы k.
Расчет полученной вероятности ложных тревог проводился по формуле:
![]() (15)
(15)
где N=64 – размер цифрового скользящего окна; R – число ложных срабатываний; M=52 – количество стробов (зондирований).
Зависимость частоты ложных тревог от добавочной константы, при расчетной вероятности ложных тревог F=10-2 и F=10-3, изображена на диаграмме (рис. 6 а, б).

а) Зависимость частоты ложных тревог от добавочной константы
при логнормальном законе распределения помехи
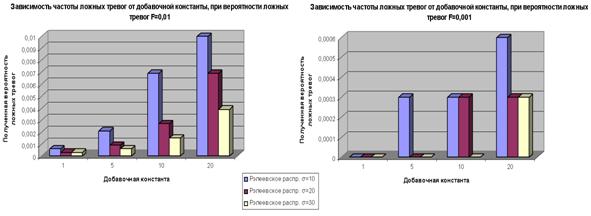
б) Зависимость частоты ложных тревог от добавочной константы
при Рэлеевском законе распределения помехи
Рис. 6. Диаграмма зависимости частоты ложных тревог от добавочной константы
Из диаграммы зависимости частоты ложных тревог от добавочной константы (рис. 6) видно, что адаптивные свойства обнаружитель log-CFAR проявляет при добавочной константе k ≥ 20 и F=10-2, при этом вероятность ложных тревог у логнормального закона распределения помехи увеличивается.
3.2. Моделирование обнаружения цели при Рэлеевском и логнормальном законе распределения помехи
Моделирование обнаружения цели проводилось при расчетной вероятности ложных тревог F=10-2 и F=10-3, и различных значениях добавочной константы k; цель формируется в середине строба; отношение сигнал/помеха рассчитывалась по 50% правильному срабатыванию (при обнаружении с вероятностью D=0,5) и D=0,9, данные критерии выбирались исходя из литературы [5, 7].
Отношение сигнал/помеха вычисляется по формуле:
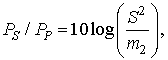 (16)
(16)
где S –мощность цели (дБ); m2 – момент распределения второго порядка.
Момент распределения второго порядка вычисляется по формуле:
![]() (17)
(17)
где m1 – математическое ожидание логнормального закона; M2 – дисперсия логнормального закона.
Математическое ожидание логнормального закона:
![]() (18)
(18)
где μ – математическое ожидание нормального закона, σ2 – дисперсия нормального закона.
Дисперсия логнормального закона:
![]() (19)
(19)
Для Рэлеевского закона момент распределения первого порядка вычисляется по формуле:
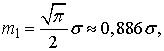 (20)
(20)
Дисперсия Рэлеевского закона или центральный момент второго порядка вычисляется по формуле:
![]() (21)
(21)
Зависимость отношения сигнал/помеха относительно добавочной константы, при расчетной вероятности ложных тревог F=0,01, F=0,001, вероятности правильного обнаружения D=0,5 и D=0,9 изображена на диаграмме (Рис. 6 а, б).

а) Зависимость отношения сигнал/помеха относительно добавочной константы, при логнормальном законе распределения помехи
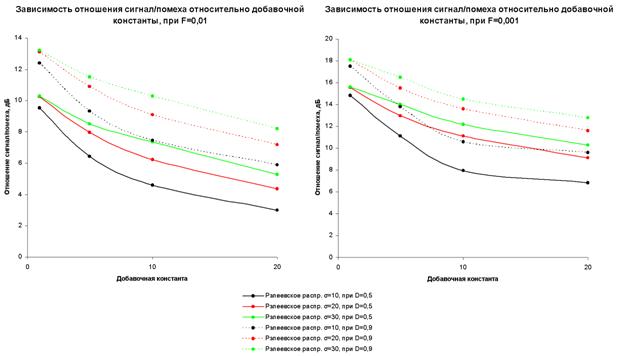
б) Зависимость отношения сигнал/помеха относительно добавочной константы, при Рэлеевском законе распределения помехи
Рис. 6. Диаграмма зависимости отношения сигнал/помеха относительно добавочной константы
Для оценки потерь отношения сигнал/помеха возникающих в результате влияния добавочной константы, проведено имитационное моделирование при отсутствии квантования по уровню на входе логарифмической функции и минимальным значением добавочной константы k=0,1. Результат моделирования при отсутствии квантования по уровню показан в таблице 6.
Таблица 6.
Параметры закона распределения помехи
Расчетная вероятность ложных тревог
Отношение сигнал/помеха (дБ), при D=0,5
Отношение сигнал/помеха (дБ), при D=0,9
Логнормальный закон μ=3,67; σ=0,422
F=10-2
10
13,22
F=10-3
14,7
17,95
Логнормальный закон μ=4,27; σ=0,286
F=10-2
6,44
11,08
F=10-3
12,16
14,87
Логнормальный закон μ=4,13; σ=0,321
F=10-2
7,2
11,9
F=10-3
13
15,9
Рэлеевский закон
σ=10
F=10-2
10,89
13,81
F=10-3
16,2
18,8
Рэлеевский закон
σ=20
F=10-2
10,89
13,81
F=10-3
16,26
18,8
Рэлеевский закон
σ=30
F=10-2
10,89
13,81
F=10-3
16,2
18,8
Потери в отношении сигнал/помеха, возникающие в результате влияния добавочной константы, при правильном обнаружении цели с вероятностью D=0,5 и D=0,9, изображены на диаграмме (рис. 7 а, б).
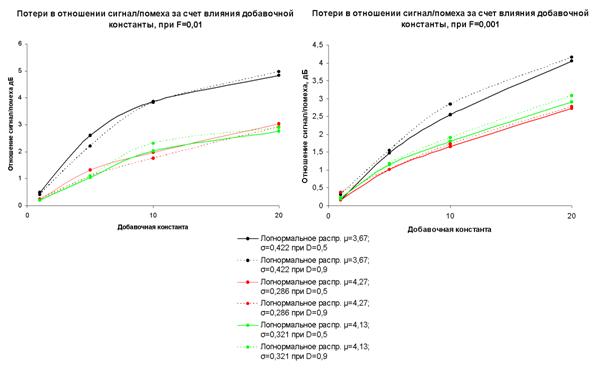
а) Потери в отношении сигнал/помеха при логнормальном законе распределения помехи

б) Потери в отношении сигнал/помеха при Рэлеевском законе распределения помехи
Рис. 7. Потери в отношении сигнал/помеха
Анализ результатов диаграммы (Рис. 5 а, б) и (рис. 6 а, б) позволяет сделать следующие выводы:
1. Введение константы k приводит к существенно меньшим изменениям величины F при смене законов распределения помех. Зависимость FMAX / FMIN от добавочной константы k, приведена на рис. 8.
2. При увеличении добавочной константы k происходит уменьшение отношения сигнал/помеха, при соответственном увеличении ложных тревог.
3. При введении добавочной константы k, также наблюдаются потери в отношении сигнал/помеха (Рис 7 а, б).
4. При увеличении вероятности обнаружения D с 0,5 до 0,9 отношение сигнал/помеха изменяется в пределах +3 дБ, данный показатель удовлетворяет характеристике обнаружения сигнала при вероятности ложных тревог F=10-2 и F=10-3 [7].

Рис. 8. Зависимость FMAX/FMIN от k, при F=10-2 и F=10-3
3.3 Моделирование переходных процессов
Переходные процессы, связанные с непостоянством метеоусловий, отрицательно влияют на обнаружение полезной цели. При моделировании переходных процессов в обнаружителе log-CFAR примем во внимание, что смена распределения помех происходит вне строба, поскольку метеоусловия протекают с большим интервалом времени.
Моделирование переходных процессов проводилось при переходе с Рэлеевского (σ=10) на логнормальное распределение помехи (μ=3,67; σ=0,422) и, наоборот, при этом добавочная константа k имела различные значения; вероятность ложных тревог составляла F=10-2 и F=10-3.
Наглядное отображение пропуска цели, при переходном процессе с логнормального на Рэлеевский закон распределения помехи, где добавочная константа k=10 и вероятность ложных тревог F=10-3 показано на Рис. 9.

Рис. 9. Пропуск цели при переходном процессе с логнормального на
Рэлеевский закон распределения помехи
При увеличении добавочной константы явление пропуска цели исчезает Наглядное отображение переходного процесса с логнормального на Рэлеевский закон распределения помехи, где явление пропуска цели не наблюдается (рис. 10), при добавочной константе k=20 и F=10-3.
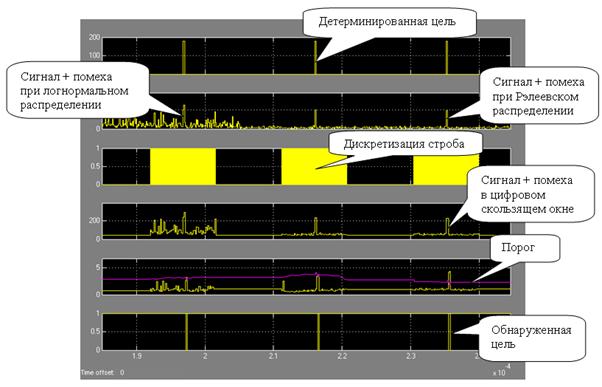
Рис. 10. Отсутствие пропуска цели при переходном процессе с логнормального на Рэлеевский закон распределения помехи
Заключение
Для обнаружения полезной цели на фоне морских помех, в данной статье описан обнаружитель log-CFAR. Особенность обнаружителя log-CFAR заключается в том, что он способен работать, как при прямой видимости цели, когда помехи описываются Рэлеевским законом распределения, так и при плохих метеоусловий, описываемых логнормальным законом распределения, это достигается за счет добавочной константы, стоящей перед функцией логарифма.
Введение добавочной константы перед логарифмическим преобразованием входного сигнала в схеме обнаружителя log-CFAR позволяет существенно снизить влияние закона распределения морских помех на стабилизацию частоты ложных тревог, увеличивая при этом потери в отношении сигнал/помеха.
Переходные процессы, связанные со сменой метеоусловий, компенсируются в обнаружителе log-CFAR также за счет экспериментального подбора добавочной константы.
Моделирование принципа работы обнаружителя log-CFAR на фоне двух видов помех показало удовлетворительные результаты. Использование обнаружителя log-CFAR на фоне морских помех, позволяет существенно упростить алгоритм работы обнаружителя, а также избавиться от карты помех.
Литература
1. Sayama S., Ishii S. Suppression of Log-Normal Distributed Weather Clutter Observed by an S-Band Radar / S. Sayama, S. Ishii. – Wireless Engineering and Technology, 4, 2013. – 125-133 p.
2. Е. А. Милащенко, В. Г. Валеев. Прогнозирование характеристик обнаружения мелких морских целей с учетом негауссовских морских отражений применительно к когерентно-импульсной РЛС. // Журнал радиоэлектроники: электронный журнал. 2014. №3. URL: http://jre.cplire.ru/mac/mar14/2/text.pdf
3. Ward K., Tough R. Sea Clutter. Scattering, the K Distribution and Radar Performance / K. Ward, R. Tough. – Croydon.: CPI Group Ltd, 2013. – 586 p.
4. Alaa S. Hafez. A New Differential Clutter Map Processingin Modern Surveillance Radars / Alaa S. Hafez – XXIV National radio science conference, 2007. – 6 p.
5. Musha T., Sekine M. CFAR Techniques in clutter. Advanced radar techniques and systems. ed. Gaspare Galate / T. Musha, M. Sekine. – Peter Peregrinus Ltd, 1993 – 1113 p.
6. Takeru I. Adaptive constant false alarm rate (CFAR) processor / I. Takeru. – US Patent №4513286, 23 Apr., 1985.
7. Сколник М. Справочник по радиолокации / М. Сколник. – Том 1. Основы радиолокации. Под ред. Я.С. Ицхоки. – М., "Сов. радио", 1976. – 456 с.