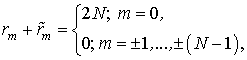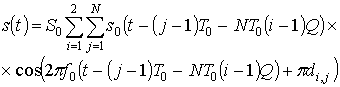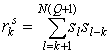Когерентные дополнительные сигналы и их применение в радиолокации

УДК 621.391.81:621.396.96

когерентные дополнительные сигналы и их применение в радиолокации

Р. Н. Ипанов

Федеральное казенное учреждение «Научно-производственное объединение «Специальная техника и связь» МВД России

Статья получена 26 января 2015 г. после доработки – 16 февраля 2015 г.

Аннотация. Рассмотрены радиолокационные сигналы, имеющие в окрестности центрального пика автокорреляционной функции область нулевых боковых лепестков. Это позволяет с высокими показателями качества решать задачи разрешения и измерения координат групповых целей с малыми эффективными поверхностями рассеяния и близкими радиальными скоростями.

Ключевые слова: когерентный сигнал, ортогональный сигнал, комплексная огибающая, автокорреляционная функция.

Abstract. The radar signals having zone of zero side lobes in the vicinity of major lobe of an autocorrelation function are considered. It allows to solve problems of resolution and measuring of coordinates of multiple targets with small cross-sections and сlose range rates with high quality indexes.

Key words: coherent signal, orthogonal signal, complex envelope, autocorrelation function.

Введение

В радиолокации в настоящее время остается не решенная до конца задача разрешения распределенных по дальности целей, имеющих близкие радиальные скорости.

Как известно, принятые на вооружение вероятным противником межконтинентальные баллистические ракеты (МБР) для повышения вероятности прорыва системы противоракетной обороны оснащаются комплексом средств преодоления (КСП). Совокупность движущихся по заданным траекториям боеголовок, элементов конструкции головной части МБР, КСП и последней ступени ракетоносителя образуют сложную баллистическую цель (СБЦ).

Таким образом, задача разрешения распределенных по дальности целей, имеющих близкие радиальные скорости, есть задача разрешения элементов СБЦ, для последующей их селекции на внеатмосферном участке траектории. Это позволит увеличить время предупреждения о ракетном нападении, а значит и время для принятия решения высшим руководством страны на ответные действия.

В РЛС сопровождения целей для решения задач разрешения элементов СБЦ и измерения их координат используются ФКМ сигналы, кодируемые усеченными М-последовательностями. Как известно, автокорреляционная функция (АКФ) ФКМ сигнала, кодируемого периодом М-последовательности, имеет боковые лепестки с максимальным уровнем, стремящимся с ростом числа дискрет М-последовательности к [1]. Значит, порог обнаружения целей не может быть ниже уровня , так как в этом случае боковые лепестки АКФ будут приняты за сигналы от целей, а это приведет к пропуску целей с малой эффективной поверхностью рассеяния (ЭПР).

Цель работы – решение задач обнаружения и разрешения элементов СБЦ с высокими вероятностными характеристиками обнаружения путем применения в качестве зондирующего когерентного дополнительного сигнала, позволяющего понизить порог обнаружения до уровня шумов.

Процедура построения когерентных дополнительных сигналов

Когерентные дополнительные сигналы (КДС) представляют собой последовательность двух когерентных ФКМ импульсов, каждый из которых кодирован одной из дополнительных последовательностей.

Последовательности и называются дополнительными [2], если

(1)

где

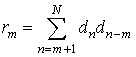- АКФ последовательности ; (2)

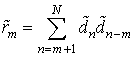- АКФ последовательности . (3)

Представим дополнительные последовательности в векторной форме :

;

Тогда согласно правилу присоединения, если , то

;

Представим нулевой вектор-строку длиной в следующем виде:

где - скважность КДС.

Т.о., огибающая КДС в векторной форме будет иметь вид следующей блочной матрицы:

. (4)

Аналитическое выражение КДС и его комплексной огибающей имеют вид соответственно:

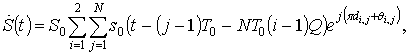(5)

где - амплитуда КДС;

при - элементарный дискрет КДС;

– длительность элементарного дискрета;

;

при и при (, ).

Анализ корреляционных характеристик когерентных дополнительных сигналов

Для анализа корреляционных характеристик КДС запишем несколько необходимых нам далее определений и свойств.

Взаимокорреляционная функция (ВКФ) дополнительных последовательностей и определяется:

, где: . (6)

В данных обозначениях две последовательности называются ортогональными, если:

, при . (7)

Для произвольных полифазных ФКМ сигналов для их АКФ выполняется равенство [2]:

Если ФКМ сигнал имеет только две фазы 0 и π, то будет иметь место частный случай:

. (8)

Представим АКФ дополнительных последовательностей в векторной форме:

;

Из определения дополнительных последовательностей (1) следует, что:

(9)

ВКФ имеет следующий вид:

Т.к. дополнительные последовательности являются ортогональными, то согласно (7) .

Обозначим АКФ КДС следующим образом:

, где . (10)

Тогда в векторной форме АКФ КДС будет иметь следующий вид:

. (11)

Далее определим зависимости значений отсчетов АКФ КДС (элементов вектора АКФ) от значений отсчетов АКФ и ВКФ дополнительных последовательностей, а также полученный при этом вид АКФ КДС при .

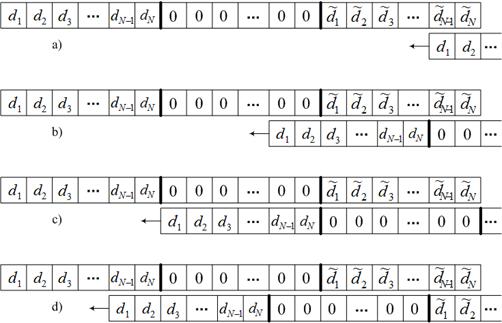
Рис.1.Этапы согласованной фильтрации КДС при .

На рис.1 графически изображены этапы алгоритма (10) согласованной фильтрации КДС при . Рассмотрим их более подробно.

Таблица 1.

Шаг согласованной фильтрации	Значения отсчетов АКФ КДС
1
2
3
…	…




…	…




…	…

В таблице 1 определяем значения отсчетов АКФ КДС из рис.1 в виде суммы произведений значений отсчетов КДС и его импульсной характеристики, по которым согласно выражениям (2), (3) и (6) определяем соответствующие им значения АКФ и ВКФ дополнительных последовательностей.

Шаг 2 соответствует рис. 1a), шаг соответствует рис. 1b), шаг соответствует рис. 1c), шаг соответствует рис. 1d).

согласно определению ортогональности (7), согласно рис. 1c), и согласно определению дополнительных последовательностей (1).

В таблице 1 определены значения боковых лепестков АКФ КДС только с одной стороны относительно основного лепестка (центрального пика). Вторая половина боковых лепестков согласно свойству ФКМ сигналов (8) будет симметрична первой относительно центрального пика.

Т.о., АКФ КДС при в векторной форме будет иметь следующий вид:

И согласно (9) и таблице 1 получаем окончательно:

При произвольном АКФ КДС в векторной форме будет иметь следующий вид (легко получить из того же рис.1):

, (12)

где:

- нулевой вектор-строка длиной .

Из (12) следует, что размер нулевой области (окрестности ), в которой значения боковых лепестков АКФ КДС равны нулю, определяется размерами двух векторов и (либо ):

С учетом длительности элементарного дискрета окончательно получаем размер нулевой окрестности АКФ КДС в абсолютных значениях времени [3]:

. (13)

Далее во всех приведенных примерах будем считать длительность элементарного дискрета равным 0,2 мкс.

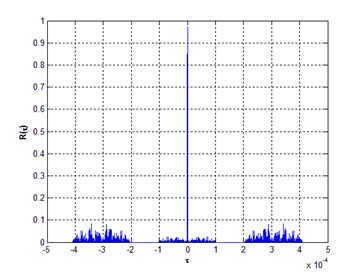
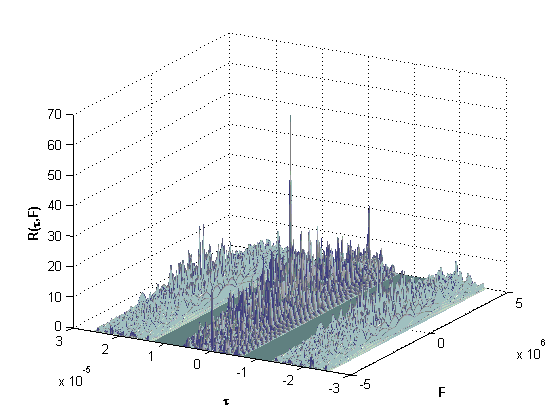
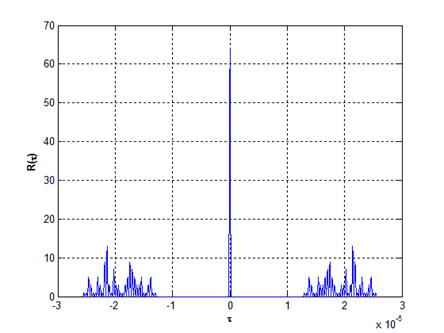
На рис.2a) и 2b) представлены соответственно тело неопределенности и его сечение плоскостью , т.е. АКФ КДС при полном согласовании фильтра с эхо-сигналом по частоте. Здесь используется зондирующий сигнал с параметрами: число дискрет в импульсе , скважность .

Рис.2. Корреляционные характеристики КДС с параметрами и .

Нулевая окрестность для сигнала с данными параметрами будет равна:

мкс.

Из рис.2a) видно, что тело неопределенности имеет две прямоугольные области с нулевыми лепестками корреляции вдоль всей оси частот . Это обусловлено наличием скважности , т.е. пачечной структурой КДС. Чем больше скважность, тем шире будут эти прямоугольные области, что подтверждается наличием вектора в выражении для АКФ КДС (12).

Нулевая окрестность в непосредственной близости от центрального пика корреляционной функции, обусловленная свойством дополнительных последовательностей (1), будет иметь место только при полном согласовании фильтра с эхо-сигналом по частоте (рис.2b)).

Рассмотрим далее, как влияет рассогласование по частоте согласованного фильтра с отраженным от цели КДС на АКФ в сравнении с эхо-сигналом, кодированным М-последовательностью. Рассогласовывать будем фильтр с эхо-сигналом в пределах одной разрешающей способности по частоте , где - длительность сигнала ( - база сигнала).

На рис.3 показана нормированная АКФ КДС с параметрами и при рассогласовании с согласованным фильтром на частоту , где (рис.3a)), (рис.3b)), (рис.3c)), (рис.3d)), (рис.3e)).

Рис.3. АКФ КДС при рассогласовании с согласованным фильтром по частоте

В таблице 2 представлены значения центрального пика и максимального бокового лепестка АКФ КДС, а также их отношение в децибелах при различных рассогласованиях по частоте в сравнении с корреляционными характеристиками усеченной М-последовательности, имеющей характеристический полином , к периоду которой добавлен один элемент с другого периода для выравнивания коэффициента сжатия с КДС.

Таблица 2.

	КДС			М-последовательность
			,			, дБ
0	1024	0	-∞	1024	39	-14,2
0,1	994,7	24,7	-16,0	1007,2	38,4	-14,2
0,2	908,6	48,1	-12,8	957,9	37,9	-14,0
0,5	381,9	97,7	-5,9	651,9	42,4	-11,9
1	651,9	75,7	-9,4	0	44,3	-

Из таблицы 2 следует, что нулевую окрестность АКФ КДС имеет только при полном согласовании сигнала с фильтром по частоте. При рассогласовании появляются боковые лепестки корреляции в окрестности центрального пика, уровень которых приемлем, т.е. сопоставим с уровнем боковых лепестков АКФ М-последовательности, только при небольшом рассогласовании по частоте .

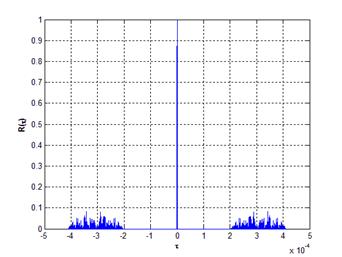
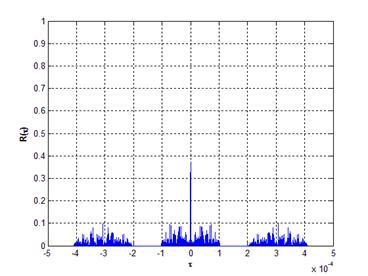
В окончании посмотрим, как будет выглядеть сигнал на выходе согласованного фильтра, представляющий собой аддитивную смесь белого гауссовского шума с двумя сигналами, отраженными от целей с различными ЭПР.

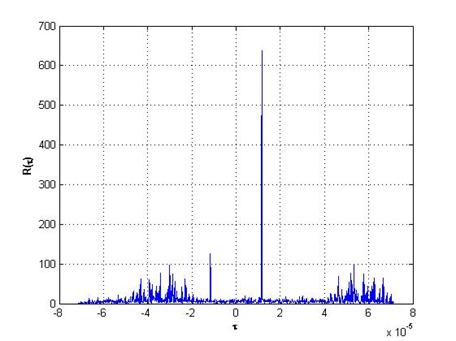
a) , , ,

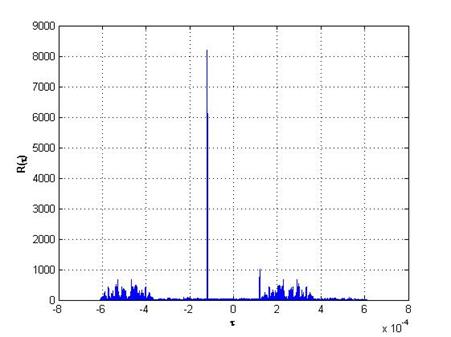
b) , , ,

Рис.4. Аддитивная смесь двух сигналов с белым гауссовским шумом на выходе согласованного фильтра

На рис.4 представлен сигнал на выходе согласованного фильтра для двух случаев:

a) число дискрет в импульсе КДС , амплитуда первого сигнала , амплитуда второго сигнала в пять раз больше первого , один сигнал сдвинут относительно другого по времени на ;

b) число дискрет в импульсе КДС , амплитуда первого сигнала , амплитуда второго сигнала , один сигнал сдвинут относительно другого по времени на .

В обоих случаях отношение сигнал/шум на входе согласованного фильтра равно 1 дБ.

Как видно из рис.4, нулевая окрестность АКФ КДС позволяет обнаруживать эхо-сигналы от целей с малой ЭПР на фоне белого шума с более сильным (в разы) эхо-сигналом.

Выводы

Когерентные дополнительные сигналы, благодаря своим корреляционным свойствам, позволяют решать задачу обнаружения радиолокационных целей с малой ЭПР с высокими вероятностными характеристиками обнаружения. Также за счет относительно большой базы эти сигналы имеют высокие коэффициенты сжатия, что позволяет решать задачу разрешения близкорасположенных по дальности целей с близкими радиальными скоростями, то есть элементов СБЦ, и измерять их координаты с высокими точностными характеристиками.

Литература

1. Амиантов И.Н. Избранные вопросы статистической теории связи. М.: Сов. радио, 1971. 416 с.

2. Варакин Л.Е. Теория сложных сигналов. М.: Сов. радио, 1970. 376 с.

3. Ипанов Р.Н., Сухоруков В.И., Щетинин В.И. Сопоставительная оценка корреляционных характеристик полифазных ФКМ сигналов. // Естественные и технические науки. 2004, №2, с. 170-173.