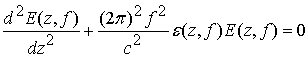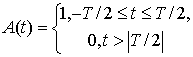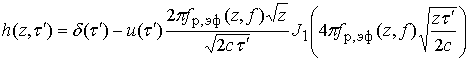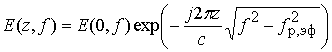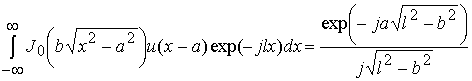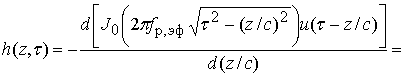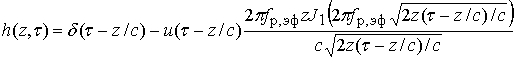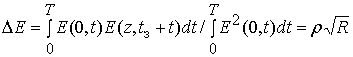УДК 621.391.01
ИСКАЖЕНИЯ РАДИОИМПУЛЬСОВ ПРИ РАСПРОСТРАНЕНИИ ПО ИОНОСФЕРНЫМ ЛИНИЯМ СПУТНИКОВЫХ СИСТЕМ СВЯЗИ
Л. Е. Назаров1, В. В. Батанов2, А. С. Зудилин 2
1Фрязинский
филиал Института радиотехники и электроники им. В.А.Котельникова РАН, г.
Фрязино
2АО «Информационные спутниковые
системы» им. академика М.Ф.Решетнева, г. Железногорск
Статья поступила в редакцию 29 января 2016 г.
Аннотация. Приведены методы представления во временной области радиоимпульсов при их распространении по ионосферным линиям передачи спутниковых цифровых систем связи, оценивание искажений произведено с использованием взаимно-корреляционного анализа радиоимпульсов с искажениями и без искажений.
Ключевые слова: ионосферные линии, радиоимпульсы, искажения радиоимпульсов.
Abstract. The propagation of short impulse-like pulses propagating through the ionospheric satellite communication channels is studied in the article. The description of impulse distortion is based on the time-impulse response for ionosphere channel.
Key words: ionosphere, radio impulse, distortion.
Введение
При распространении по линиям передачи спутниковых систем связи сигналы подвергаются искажающему действию ряда факторов, основными из которых являются следующие [1-4]:
- влияние ионосферы и тропосферы;
- многолучевость за счет рассеяния, дифракции и отражения сигналов;
- доплеровское смещение и уширение спектра сигналов;
- нестационарность линий передачи;
- наличие аддитивного шума.
Созданию и развитию класса моделей относительно действия этих факторов посвящен ряд работ [1,4-9]. Эти модели позволяют оценить энергетические потери при обработке сигналов в приемных устройствах по отношению к случаю распространения сигналов в свободном пространстве.
В данной статье рассмотрена проблема оценивания искажения радиоимпульсов, представляющих базовые элементы для сигналов с цифровой манипуляцией, при распространении по ионосферным спутниковым линиям передачи [1]. Ионосфера является неоднородной дисперсионной средой распространения, которая обусловливает фазо-частотные и амплитудно-частотные искажения радиоимпульсов [2,11]. Проблема анализа искажений радиоимпульсов при их распространении по ионосферным линиям актуальна для спутниковых систем цифровой связи различных частотных диапазонов и различного назначения (низкоорбитальные, среднеорбитальные, геостационарные, высокоэллиптические) [1], для спутниковых систем навигации [10], для систем мониторинга ионосферы [7].
Рассматриваемые искажения приводят к возникновению межсимвольных и межканальных помех при передаче цифровых сигналов в дополнение к аддитивным канальным тепловым шумам, к энергетическим потерям при корреляционной обработке рассматриваемых радиоимпульсов, составляющих основу процедур тематического анализа характеристик ионосферы и обнаружения сигналов при установлении синхронизации (тактовой, частотной, фазовой) в цифровых системах связи.
В данной статье приведены
методы описания распространяемых радиоимпульсов во временной области с
использованием импульсной характеристики ![]() ионосферных
линий. Оценивание искажений произведено с использованием
взаимно-корреляционного анализа радиоимпульсов с искажениями и без искажений.
ионосферных
линий. Оценивание искажений произведено с использованием
взаимно-корреляционного анализа радиоимпульсов с искажениями и без искажений.
1. Постановка задачи
В соответствии с Регламентом радиосвязи для спутниковых систем связи выделены P-, L-, S-, Х-, K- частотные диапазоны, интенсивно осваиваются другие частотные диапазоны [1].
При распространении по
спутниковым линиям передачи происходит искажение фазо-частотных характеристик
передаваемых сигналов за счет дисперсионных свойств ионосферы. Основу методов
анализа эффективности данного влияния ионосферы составляет решение волнового
уравнения при распространении по оси ![]() плоской волны
плоской волны ![]() с частотой
с частотой ![]() ,
нормально падающей на слой неоднородной среды с диэлектрической проницаемостью
,
нормально падающей на слой неоднородной среды с диэлектрической проницаемостью ![]() [2]
[2]
Здесь ![]() - скорость света в вакууме.
- скорость света в вакууме.
В общем случае для
произвольной функции ![]() уравнение (1) не имеет решения,
представимого через известные функции. Ряд аналитических решений получен при
использовании упрощений относительно
уравнение (1) не имеет решения,
представимого через известные функции. Ряд аналитических решений получен при
использовании упрощений относительно ![]() , полагая, в частности,
среду распространения изотропной (модель «холодной» плазмы), а также
плоскослоистой или сферически слоистой [2]. Например, при этих условиях решение
(1) для слоя с линейной зависимостью диэлектрической проницаемости от
, полагая, в частности,
среду распространения изотропной (модель «холодной» плазмы), а также
плоскослоистой или сферически слоистой [2]. Например, при этих условиях решение
(1) для слоя с линейной зависимостью диэлектрической проницаемости от ![]() выражается через функции Бесселя порядка
1/3 [2].
выражается через функции Бесселя порядка
1/3 [2].
Важным направлением
является определение приближенных решений волнового уравнения (1), в частности,
приближение геометрической оптики. Достаточным условием применимости этого
приближения является медленность изменения диэлектрических свойств среды на
длине волны ![]() , т. е.
, т. е.
![]() или
или
 [2].
[2].
Здесь ![]() -
коэффициент преломления среды.
-
коэффициент преломления среды.
Приближение геометрической оптики к решению волнового уравнения без учета отражения для неоднородной ионосферы имеет вид [2]
Более точное приближение геометрической оптики к решению волнового уравнения для неоднородной ионосферы задается соотношением
Соотношения (2), (3)
справедливы для монохроматических волн. При распространении радиоимпульса
длительностью ![]() с центральной частотой
с центральной частотой ![]() , задаваемого в виде
, задаваемого в виде
и представляющего спектр монохроматических волн, задача усложняется. В этом случае каждая спектральная компонента при распространении приобретает частное фазовое смещение и частное изменение амплитуды, что обусловливает искажение радиоимпульса на входе приемного устройства.
В соотношении (4)
обозначение ![]() соответствует огибающей радиоимпульса, ее
примером является меандр
соответствует огибающей радиоимпульса, ее
примером является меандр
Суть задачи - оценивание влияния искажений радиоимпульсов при распространении по неоднородной ионосферной спутниковой линии передачи, эффективность искажений производится на основе взаимно-корреляционного анализа радиоимпульсов с искажениями и без искажений.
2. Модели ионосферы
Для частот ![]() , используемых в системах спутниковой
связи, коэффициент диэлектрической проницаемости ионосферы
, используемых в системах спутниковой
связи, коэффициент диэлектрической проницаемости ионосферы ![]() в виде неоднородной
сферически-симметричной среды задается соотношением [3,4]
в виде неоднородной
сферически-симметричной среды задается соотношением [3,4]
Здесь ![]() - собственная
частота ионосферы (кГц);
- собственная
частота ионосферы (кГц); ![]() - электронная
плотность ионосферы (эл/см3) на высоте
- электронная
плотность ионосферы (эл/см3) на высоте ![]() .
.
Данная модель
диэлектрической проницаемости ![]() (6) является
вещественной, явления отражения, рассеяния и поглощения радиоволн для
рассматриваемых частотных диапазонов полагаются малыми. Это обусловливает лишь
фазо-частотные искажения при распространении радиоимпульсов.
(6) является
вещественной, явления отражения, рассеяния и поглощения радиоволн для
рассматриваемых частотных диапазонов полагаются малыми. Это обусловливает лишь
фазо-частотные искажения при распространении радиоимпульсов.
Разработке и развитию
моделей профиля электронной плотности ионосферы ![]() посвящен
ряд работ [1,3,4,10]. Известная и наиболее простая модель электронной плотности
ионосферы
посвящен
ряд работ [1,3,4,10]. Известная и наиболее простая модель электронной плотности
ионосферы ![]() , используемая ниже, имеет вид [3]
, используемая ниже, имеет вид [3]
Здесь ![]() -
параметры модели;
-
параметры модели; ![]() - высота над земной
поверхностью, для которой достигается максимальное значение электронной
плотности.
- высота над земной
поверхностью, для которой достигается максимальное значение электронной
плотности.
Например, для дневного
времени максимальное значение ![]() эл/см
эл/см![]() [2] (параметры модели
[2] (параметры модели ![]() ,
, ![]() ,
, ![]() км), соответствующее значение собственной
частоты ионосферы для
км), соответствующее значение собственной
частоты ионосферы для ![]() равно
равно ![]() МГц.
Для ночного времени максимальное значение
МГц.
Для ночного времени максимальное значение ![]() эл/см
эл/см![]() [2] (параметры модели
[2] (параметры модели ![]() ,
, ![]() ,
, ![]() км), значение собственной частоты
ионосферы для
км), значение собственной частоты
ионосферы для ![]() равно
равно ![]() МГц.
МГц.
3. Описания искажений радиоимпульсов
Методы анализа
рассматриваемых искажений при распространении радиоимпульсов можно отнести к
двум общим классам. В первый класс входят методы анализа искажений во временной
области с использованием импульсной характеристики ![]() ионосферной
линии [8, 11]. Во второй класс входят методы анализа искажений в частотной
области с использованием аппарата спектрального преобразования Фурье [2,5].
ионосферной
линии [8, 11]. Во второй класс входят методы анализа искажений в частотной
области с использованием аппарата спектрального преобразования Фурье [2,5].
Представления
радиоимпульса ![]() с использованием импульсной
характеристики
с использованием импульсной
характеристики ![]() ионосферной линии задается
соотношением свертки
ионосферной линии задается
соотношением свертки
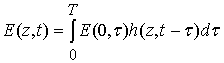 .
(8)
.
(8)
Методы анализа искажений из второго класса основаны на вычислении обратного преобразования Фурье
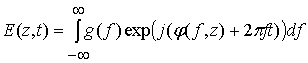 .
(9)
.
(9)
Здесь ![]() -
спектр радиоимпульса, в частности, для радиоимпульса с огибающей в виде меандра
(5) имеем
-
спектр радиоимпульса, в частности, для радиоимпульса с огибающей в виде меандра
(5) имеем

при условии ![]() ,
, ![]() - центральная частота радиоимпульса;
- центральная частота радиоимпульса;
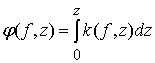 - фаза спектральной компоненты для
частоты
- фаза спектральной компоненты для
частоты ![]() ;
;
![]() - волновое число.
- волновое число.
Ниже рассматриваются методы анализа искажений радиоимпульсов из первого класса.
4. Описание искажений радиоимпульсов во временной области при распространении в неоднородной ионосфере
Импульсная характеристика
![]() для стационарной неоднородной ионосферы
при определенных допущениях может быть представлена в виде приближенного
аналитического выражения. Одно из таких выражений приведено в [8]
для стационарной неоднородной ионосферы
при определенных допущениях может быть представлена в виде приближенного
аналитического выражения. Одно из таких выражений приведено в [8]
Здесь ![]() -
дельта-функция;
-
дельта-функция; ![]() ;
; ![]() -
функция единичного скачка;
-
функция единичного скачка; 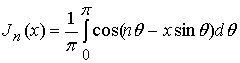 - функция Бесселя
- функция Бесселя ![]() -го порядка [12]. Для неоднородной
ионосферы ее эффективное значение собственной частоты
-го порядка [12]. Для неоднородной
ионосферы ее эффективное значение собственной частоты ![]() для
для
![]() определяется как решение уравнения
определяется как решение уравнения
При вычислении (11)
используется модель профиля ![]() (7).
(7).
Для частотного диапазона
спутниковых линий передачи выполняется условие ![]() и
вычисление
и
вычисление ![]() можно производить с использованием
соотношения
можно производить с использованием
соотношения 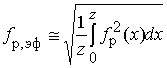 . При этом эффективная
собственная частота
. При этом эффективная
собственная частота ![]() практически не зависит от
значений центральной частоты
практически не зависит от
значений центральной частоты ![]() и функционально
связана с полным электронным содержанием (ПЭС)
и функционально
связана с полным электронным содержанием (ПЭС) 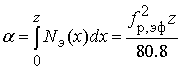 . ПЭС
является одной из основных характеристик ионосферы Земли [4], определяющей
задержку времени распространения радиоимпульсов в неоднородной ионосфере по
отношению к распространению в свободном пространстве, а также частные фазовые
смещения для составляющих спектральных компонент сигналов.
. ПЭС
является одной из основных характеристик ионосферы Земли [4], определяющей
задержку времени распространения радиоимпульсов в неоднородной ионосфере по
отношению к распространению в свободном пространстве, а также частные фазовые
смещения для составляющих спектральных компонент сигналов.
Ниже даны выкладки для
второго аналитического выражения ![]() [11]. Соотношение (2)
представляет решение волнового уравнения (1) для плоской монохроматической
волны с частотой
[11]. Соотношение (2)
представляет решение волнового уравнения (1) для плоской монохроматической
волны с частотой ![]() . С использованием
. С использованием ![]() решение волнового уравнения (2) для
решение волнового уравнения (2) для ![]() имеет вид
имеет вид
Импульсная характеристика
![]() , задаваемая входным импульсом в виде
дельта-функции
, задаваемая входным импульсом в виде
дельта-функции ![]() , с учетом (11) имеет формальное
представление в виде
, с учетом (11) имеет формальное
представление в виде
Дельта-функция ![]() имеет бесконечный равномерный спектр.
Известно, что радиоволны с частотой
имеет бесконечный равномерный спектр.
Известно, что радиоволны с частотой ![]() не распространяются в
ионосфере и в окрестности
не распространяются в
ионосфере и в окрестности ![]() не выполняется
приближение геометрической оптики. Поэтому использование соотношения (12),
справедливое для узкополосных процессов, определяет приближенное выражение
импульсной характеристики в виде (13) для ионосферной линии.
не выполняется
приближение геометрической оптики. Поэтому использование соотношения (12),
справедливое для узкополосных процессов, определяет приближенное выражение
импульсной характеристики в виде (13) для ионосферной линии.
Для представления ![]() аналитическим выражением используется интегральное
тождество [12]
аналитическим выражением используется интегральное
тождество [12]
Здесь ![]() -
параметры (
-
параметры (![]() ).
).
На основе (13), (14)
имеем результирующее выражение для ![]()
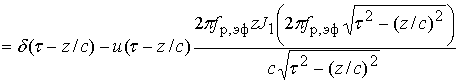 . (15)
. (15)
При выводе (15) использованы тождества
![]() ,
, ![]() [12].
[12].
Асимптотические значения
импульсных характеристик ![]() , задаваемых
соотношением (10) при
, задаваемых
соотношением (10) при ![]() и соотношением (15) при
и соотношением (15) при ![]() , совпадают и равны
, совпадают и равны 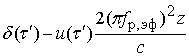 . Кроме того, для линий спутниковых
цифровых систем связи выполняется условие
. Кроме того, для линий спутниковых
цифровых систем связи выполняется условие ![]() (
(![]() - длительность радиоимпульса). Поэтому
имеем
- длительность радиоимпульса). Поэтому
имеем ![]() и можем записать выражение (15) в виде
и можем записать выражение (15) в виде
В этом случае это выражение совпадает с выражением (10).
Искажения радиоимпульса ![]() при применении корреляционной обработке
обусловливают наличие энергетических потерь
при применении корреляционной обработке
обусловливают наличие энергетических потерь ![]() по отношению
к распространению радиоимпульса в свободном пространстве и заключаются в двух
факторах. Во-первых, происходит временное рассеяние радиоимпульса за счет
возникновения сигнала-предвестника и сигнала-последействия при распространении
в ионосферной линии [2]. Вследствие этого уменьшается энергия радиоимпульса
по отношению
к распространению радиоимпульса в свободном пространстве и заключаются в двух
факторах. Во-первых, происходит временное рассеяние радиоимпульса за счет
возникновения сигнала-предвестника и сигнала-последействия при распространении
в ионосферной линии [2]. Вследствие этого уменьшается энергия радиоимпульса ![]() на интервале анализа
на интервале анализа ![]() , где временная задержка
, где временная задержка ![]() соответствует максимальному значению нормированного
коэффициента взаимной корреляции
соответствует максимальному значению нормированного
коэффициента взаимной корреляции 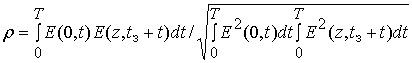 . Уменьшение энергии
радиоимпульса
. Уменьшение энергии
радиоимпульса ![]() по отношению к энергии
переданного радиоимпульса
по отношению к энергии
переданного радиоимпульса ![]() в этом случае может
быть оценено с использованием соотношения
в этом случае может
быть оценено с использованием соотношения 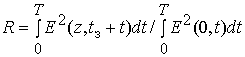 . Время
задержки
. Время
задержки ![]() для узкополосных сигналов определяется
групповой скоростью
для узкополосных сигналов определяется
групповой скоростью ![]() [2-5]. Уменьшение энергии
радиоимпульса
[2-5]. Уменьшение энергии
радиоимпульса ![]() по отношению к энергии
переданного радиоимпульса
по отношению к энергии
переданного радиоимпульса ![]() может быть оценено с
использованием соотношения
может быть оценено с
использованием соотношения 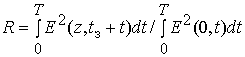 .
.
Во-вторых, изменяется
огибающая ![]() по отношению к огибающей радиоимпульса
по отношению к огибающей радиоимпульса ![]() , что определяется нормированным
коэффициентом взаимной корреляции.
, что определяется нормированным
коэффициентом взаимной корреляции.
Результирующая оценка
энергетических потерь ![]() , включающая эти факторы, может
быть произведена с использованием соотношения
, включающая эти факторы, может
быть произведена с использованием соотношения
5. Результаты вычислений
На рис.1 приведена
зависимость значений эффективной собственной частоты ионосферы ![]() от высоты
от высоты ![]() ионосферной
линии. Зависимость вычислена с использованием соотношения (11) для центральной
частоты
ионосферной
линии. Зависимость вычислена с использованием соотношения (11) для центральной
частоты ![]() МГц с использованием рассмотренной модели
высотного профиля
МГц с использованием рассмотренной модели
высотного профиля ![]() (7) для дневного времени. Из
рис.1 видно монотонное уменьшение значений
(7) для дневного времени. Из
рис.1 видно монотонное уменьшение значений ![]() при
увеличении высоты
при
увеличении высоты ![]() .
.
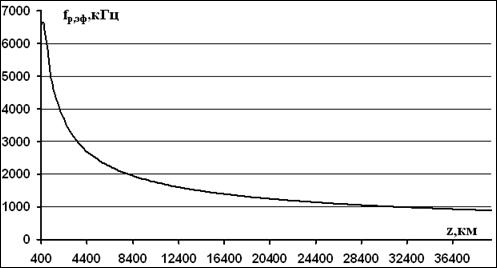
Рис.1. Зависимость значений эффективной собственной
частоты ионосферы ![]() от высоты
от высоты ![]() (день, центральная частота
(день, центральная частота ![]() МГц).
МГц).
На рис.2 приведен вид второго
слагаемого импульсной характеристики ![]() (15) без учета
дельта-функции и без учета знака. Кривая вычислена для высоты
(15) без учета
дельта-функции и без учета знака. Кривая вычислена для высоты ![]() км и
км и ![]() МГц
(соответствует ночному времени). Видно, что импульсная характеристика обладает
достаточно большой протяженностью. Это определяет протяженность последействия
искаженных радиоимпульсов и, как следствие, наличие межсимвольной интерференции
при передаче цифровых сигналов.
МГц
(соответствует ночному времени). Видно, что импульсная характеристика обладает
достаточно большой протяженностью. Это определяет протяженность последействия
искаженных радиоимпульсов и, как следствие, наличие межсимвольной интерференции
при передаче цифровых сигналов.

Рис.2. Вид второго слагаемого импульсной характеристики
![]() (15) без учета знака (высота
(15) без учета знака (высота ![]() км,
км, ![]() МГц).
МГц).
На рис.3. приведен вид
исходного радиоимпульса (кривая 1) с огибающей в виде меандра, центральная
частота радиоимпульса равна ![]() МГц, длительность
МГц, длительность ![]() нсек. Кривая 2 вычислена с использованием
соотношения (15) и соответствует радиоимпульсу при распространении в ионосфере,
характеризуемой эффективным значением собственной частоты
нсек. Кривая 2 вычислена с использованием
соотношения (15) и соответствует радиоимпульсу при распространении в ионосфере,
характеризуемой эффективным значением собственной частоты ![]() МГц, высота ионосферы над земной
поверхностью равна
МГц, высота ионосферы над земной
поверхностью равна ![]() км. Видно, что в искаженный
радиоимпульс имеет “предвестник” [2], а также отмеченное выше последействие
радиоимпульсов. Различие времени появления исходного импульса
км. Видно, что в искаженный
радиоимпульс имеет “предвестник” [2], а также отмеченное выше последействие
радиоимпульсов. Различие времени появления исходного импульса ![]() для модели распространения в
свободном пространстве и импульса
для модели распространения в
свободном пространстве и импульса ![]() на выходе ионосферной линии
обусловлено отличием групповой скорости
на выходе ионосферной линии
обусловлено отличием групповой скорости ![]() от скорости света
от скорости света ![]() .
.
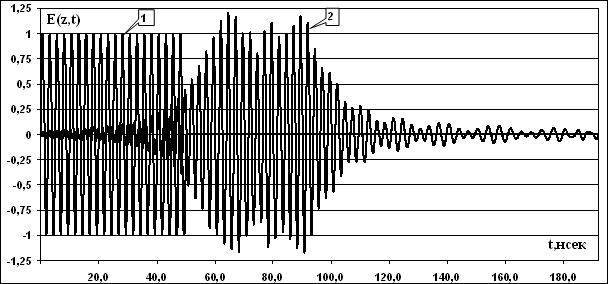
Рис.3. Вид исходного радиоимпульса ![]() (кривая 1,
(кривая 1, ![]() МГц,
МГц, ![]() нсек), вид радиоимпульса при
распространении в ионосфере
нсек), вид радиоимпульса при
распространении в ионосфере ![]() (кривая 2,
(кривая 2, ![]() МГц,
МГц, ![]() км).
км).
Таблица 1.
Оценки энергетических потерь ![]() при распространении
радиоимпульсов по ионосферным линиям передачи в зависимости от длительности
при распространении
радиоимпульсов по ионосферным линиям передачи в зависимости от длительности ![]() (полосы
(полосы ![]() )
радиоимпульсов (
)
радиоимпульсов (![]() МГц, центральная частота
МГц, центральная частота ![]() МГц,
МГц, ![]() км).
км).
|
|
|
|
|
12.5 |
160 |
-3.08 |
|
16.6 |
120 |
-2.00 |
|
20 |
100 |
-1.32 |
|
25 |
80 |
-0.69 |
|
50 |
40 |
-0.46 |
|
100 |
20 |
-0.40 |
|
200 |
10 |
-0.33 |
В таблице 1 приведены
оценки энергетических потерь![]()
![]() при
распространении радиоимпульсов по ионосферным линиям передачи, характеризуемым
параметром
при
распространении радиоимпульсов по ионосферным линиям передачи, характеризуемым
параметром ![]() . Оценки произведены с использованием изложенной
выше методики на основе результирующего соотношения (17) для значения
. Оценки произведены с использованием изложенной
выше методики на основе результирующего соотношения (17) для значения ![]() МГц (дневное время), варьируемым
параметром является длительность радиоимпульса
МГц (дневное время), варьируемым
параметром является длительность радиоимпульса ![]() (полоса
радиоимпульса
(полоса
радиоимпульса ![]() ) с центральной частотой
) с центральной частотой ![]() МГц,
МГц, ![]() км. Энергетические
потери для значения
км. Энергетические
потери для значения ![]() нсек (частотная полоса
нсек (частотная полоса ![]() МГц) достигают -0.33 дБ. При уменьшении
длительности радиоимпульса (при увеличении частотной полосы) значения
энергетических потерь
МГц) достигают -0.33 дБ. При уменьшении
длительности радиоимпульса (при увеличении частотной полосы) значения
энергетических потерь ![]() увеличиваются и для
увеличиваются и для ![]() нсек (
нсек (![]() МГц)
достигают -1.32 дБ.
МГц)
достигают -1.32 дБ.
Заключение
Приведены описания методов представления во временной области радиоимпульсов при их распространении по ионосферным линиям передачи спутниковых цифровых систем связи. Методы представления основаны на использовании модели стационарной ионосферной линии в виде линейного фильтра с импульсной характеристикой, представимой приближенным аналитическим выражением.
Проведено
оценивание искажений радиоимпульсов с использованием взаимно-корреляционного
анализа исходных радиоимпульсов и радиоимпульсов на выходе ионосферной линии
передачи, а также с использованием модельного представления неоднородной
ионосферы. Энергетические потери для радиоимпульсов с огибающей в виде меандра
с полосой до ![]() МГц и Р- частотного диапазона,
используемых в низкоорбитальных спутниковых коммуникационных системах,
достигают
МГц и Р- частотного диапазона,
используемых в низкоорбитальных спутниковых коммуникационных системах,
достигают ![]() дБ, что необходимо учитывать при расчете
энергетического бюджета.
дБ, что необходимо учитывать при расчете
энергетического бюджета.
Работа выполнена при поддержке РФФИ (№16-07-00746).
Литература
1. Спилкер Дж. Цифровая спутниковая связь. Пер. с англ. М.: Связь. 1979.
2. Гинзбург В.Л. Распространение электромагнитных волн в плазме. М.: Наука. 1967.
3. Долуханов М.П. Распространение радиоволн. М.: Гос. Издательство по вопросам связи и радио. 1960.
4. Яковлев О.И., Якубов В.П., Урядов В.П., Павельев А.Г. Распространение радиоволн. М.: ЛЕНАНД. 2009.
5. Арманд Н.А. Распространение широкополосных сигналов в дисперсионных средах. // Радиотехника и электроника. 2003. Т.48. №9. Стр.1045-1057.
6. Крюковский А.С., Лукин Д.С., Кирьянова К.С. Метод расширенной бихарактеристической системы при моделировании распространения радиоволн в ионосферной плазме. // Радиотехника и электроника. 2012. Т.57. №9. Стр. 1028-1034.
7. Ефимов А.И., Самознаев Л.Н., Стрелков Г.М., Толкачев И.Е. О возможности определения интегральной электронной концентрации межпланетной трассы по искажениям сверхкороткого радиоимпульса. // Радиотехника и электроника. 2012. Т.57. №2. Стр. 160-167.
8. Стрелков Г.М., Деркач О.Г. О дисперсионных искажениях двухчастотного радиоимпульса в холодной плазменной среде. // Радиотехника и электроника. 2014. Т.59. №3. Стр. 213-226.
9. Назаров Л.Е., Батанов В.В. Назарова З.Т. Характеристики ионосферных и тропосферных линий спутниковых систем связи.// Журнал радиоэлектроники [электронный журнал]. 2015. №9. URL: http://jre.cplire.ru/jre/sep15/6/text.pdf.
10. Hofinann-Wellenhof B., Lichtenegger H., Collins J. Global Positioning System. Theory and Practice. // Springer-Verlag. New York. 1994.
11. Dvorak S.L., Dudley D.G. Propagation of Ultrawideband Electromagnetic Pulses Through Dispersive Media. // IEEE Transactions on Electromagnetic Compatibility. 1995. V.37. N2. P.192-200.
12. Градштейн И.С., Рыжик И.М. Таблицы интегралов, сумм, рядов и произведений. М.: Физматгиз. 1963.