УДК 621.391

ВЛИЯНИЕ ФРАКТАЛЬНОЙ РАЗМЕРНОСТИ СИГНАЛА НА РАСПРЕДЕЛЕНИЕ ЭНЕРГИИ В ЕГО СПЕКТРЕ

 

А. М. Шайдук ¹, С. А. Останин ^1,2

¹ГБОУ ВПО «Алтайский государственный медицинский университет», г. Барнаул

²ФГБОУ ВПО «Алтайский государственный университет», г. Барнаул

 

Статья поступила в редакцию 28 января 2016 г.

 

Аннотация. Проведено численное моделирование вариационных рядов, полученных из спектров сигналов с различной фрактальной размерностью. Исследована зависимость нормированного ранга от величины фрактальной размерности сигнала. Показано, что  доля спектра сигнала, в котором сосредоточено 80% его энергии, очень чувствительна к фрактальной размерности сигнала

Ключевые слова: вариационный ряд, спектр, фрактальная размерность.

Abstract. Numerical simulation of variational series obtained from the spectra of signals with different fractal dimension is carried out. The dependence of the normalized rank of the value of the fractal dimension of the signal is researched. It is shown that the proportion of the signal, which concentrates 80% of its energy, is very sensitive to the fractal dimension of the signal.

Key words: variational range,  spectrum, fractal dimension.

 

Вариационные ряды являются исходным объектом исследования случайных величин методами непараметрической статистики [1]. Они широко используются в прикладных задачах измерения и идентификации [2], обнаружения [3], классификации [4], надежности [5], экстремальных значений [6]  решаемых с помощью аппарата порядковых статистик в различных предметных областях.  Преимущество вариационных рядов проявляется при исследовании случайных процессов, плотность распределения вероятности которых имеет «тяжелые хвосты» или не имеет первого момента.

Естественным образом вариационные ряды получаются при построении различных рейтингов. При анализе подобных вариационных рядов естественно хочется получить оценку степени случайности и влияние процессов управления на поведение вариационного ряда. Иллюстрацией  может служить, например, «принцип Парето» (известный также как «принцип 80-20»). Парето исследовал распределение богатства и доходов в Англии XIX века. [7]. Он выяснил, что большая часть доходов и материальных ценностей принадлежит меньшинству людей в исследованных группах, относящихся к различным периодам времени и различным странам. Можно ли оценить по свойствам вариационного ряда роль динамического регулирования поведения индивидуумов или  соотношения типа принципа Парето складываются всегда при полностью случайном поведении?

 

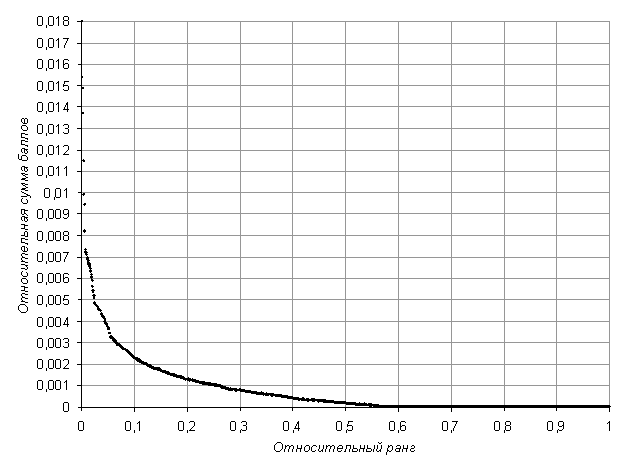
Рисунок 1. Пример вариационного ряда.  Рейтинг преподавателей одного из университетов России
минимальному значению относительного ранга соответствует максимальный рейтинг преподавателя).

 

В качестве примера на рисунке 1 приведен рейтинг преподавателей одного из университетов. Можно ли по виду этой зависимости оценить степень управления поведением преподавателей с помощью различного рода внутриуниверситетских локальных актов? Можно ли по виду этой зависимости оценить степень равенства возможностей преподавателей или на рейтинг преподавателя существенно влияет его положение в университете?  

Другим примером вариационного ряда в некотором приближении может служить спектральная плотность мощности  временного ряда x(t) с дробной размерностью (фрактала):

.                                               (1)

 

Степень  в выражении (1) связана с величиной фрактальной размерности D соотношением [8]

,                                                 (2)

 

при  или соотношением [9]

,                          (3)

при , где F – функция распределения для нормального закона.

Хотя «принцип Парето» и не носит универсального характера, представляет интерес ответ на вопрос: при каких значениях фрактальной размерности временного ряда x(t)  80% спектральной плотности мощности  сосредоточено в 20% компонентах вариационного ряда спектра? Разумеется, в качестве исходных данных вместо временного ряда x(t) может быть использована последовательность значений характеристики некоторого объекта или процесса из любой предметной области.

Для ответа на поставленный вопрос выполнены  численные эксперименты, в ходе которых моделировались временные ряды с заданной фрактальной размерностью и определялась величина доли спектра, в которой сосредоточено 80% спектральной плотности мощности .

В первой серии экспериментов временной ряд  моделировался с помощью функции Вейерштрасса-Мандельброта [10, 11] в виде

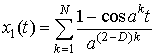                                            (4)

где D – фрактальная размерность сигнала , k – номер гармоники, N – количество гармоник, а – произвольное число, большее единицы.

         Во второй серии экспериментов временной ряд  моделировался путем преобразования спектра нормального шума  [12]:

,                                (5)

где  –  оператор преобразования Фурье,  –  оператор обратного преобразования Фурье,  –  передаточная функция,  – максимальная частота спектра. Примеры модельных временных рядов  и  с фрактальной размерностью  показаны на рисунках 1, 2.

 

Рис. 1. Модель временного ряда  на основе функции Вейерштрасса (фрактальная размерность 1,9).

 

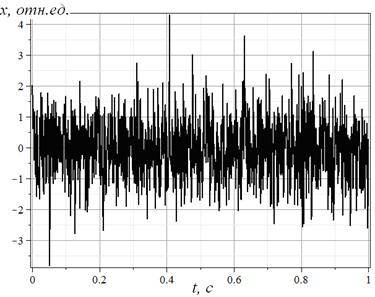
Рис. 2. Модель временного ряда  на основе преобразования нормального шума (фрактальная размерность 1,9).

 

         Для модельных временных рядов  и  с различной фрактальной размерностью вычислены спектры мощности (пример спектра  временного ряда  показан на рисунке 3), из которых сформированы вариационные ряды спектров путем ранжирования компонент спектра по убыванию их величины. Пример зависимости нормированного вариационного ряда спектра  временного ряда  от нормированного ранга r показан на рисунке 4.

 

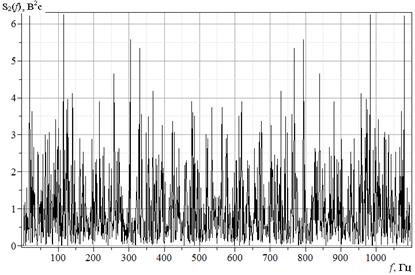
Рис. 3. Спектр мощности  временного ряда   с фрактальной размерностью 1,9.

 

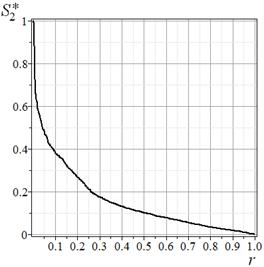
Рис. 4. Вариационный ряд спектра мощности  временного ряда   с фрактальной размерностью 1,9

.

Для того, чтобы определить величину доли вариационного ряда спектра мощности, в которой сосредоточено 80% мощности, для всех вариационных рядов вычислены кумулятивные  функции  вида:

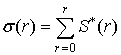                                          (6)

Пример функции  для временного ряда   с фрактальной размерностью 1,9 показан на рисунке 5. Как видно из рисунка, при фрактальной размерности  временного ряда   80% спектра мощности () сосредоточено в 43% компонент спектра ().

 

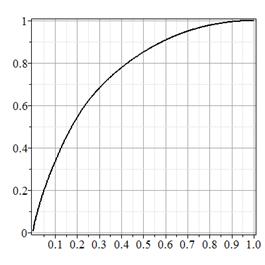
Рис. 5. Кумулятивная функция  вариационного ряда спектра .

 

Результаты численных экспериментов представлены на рисунке 6 в виде зависимостей нормированного ранга  от фрактальной размерности D временных рядов  и .  Величина нормированного ранга  получена из соотношения

                                            (9)

для вариационных рядов  и .

 

 

Рис. 6. Зависимость нормированного ранга  от фрактальной размерности D временных рядов Δ –  и ● – .

        

         Таким образом, мы видим, что доля спектра сигнала, в котором сосредоточено 80% его энергии, очень чувствительна к фрактальной размерности сигнала. Принцип Парето выполняется лишь при фрактальной размерности D=1.9, что соответствует почти полностью гауссовскому шуму. Различные способы генерации фрактального сигнала, видимо, меняют  лишь количественные значения ранга для этой доли  энергии, но не изменяют основного вывода – управляющее воздействие на сигнал, уменьшающее его фрактальную размерность, приводит к тому, что 80% энергии сигнала будет сосредоточено в  очень малой области спектра (в малой области вариационного ряда). 

 

Литература

1. Дейвид Г. Порядковые статистики / М.: Наука, 1979, 336 с.

2. Ефимов А.Н., Кутеев В.М. Безэталонные измерения и идентификация методами теории порядковых статистик //  Автоматика и телемеханика, 1978. № 12. С. 30–36.

3. Рудько И.М. Применение порядковых статистик в задачах обнаружения // Управление большими системами: сборник трудов. 2012. № 37.  С. 63-83.

4. Ефимов А.Н. Порядковые статистики – их свойства и приложения. М.: Знание, 1980. 64 с.

5. Гвоздев В.Е., Абдрафиков М.А. Статистические свойства доверительных оценок граничных значений характеристик надежности // Вестник УГАТУ, 2012. Т. 16. №8(53). С. 67–72.

6. Гумбель Э. Статистика экстремальных значений. М.: Мир, 1965. 450 с.

7. Pareto Vilfredo, Cours d’Économie Politique: Nouvelle édition par G.-H. Bousquet et G. Busino, Librairie Droz, Geneva, 1964. P. 299-345.

8. Flandrin P. On the Spectrum of Fractional Brownian Motions //IEEE Transactions on Information Theory. – 1989. V. 35. № 1. P. 197-199.

9. Останин С.А., Шайдук А.М. Уточнение отношения между фрактальной размерностью и степенью спектра мощности сигнала // Журнал радиоэлектроники: электронный журнал. 2012. N8. URL: http://jre.cplire.ru/jre/aug12/5/text.html

10. Mandelbrot B.B. The fractal geometry of nature - New York: W.H. Freeman. - 1983. 273 p.

11. Berry M. V., Lewis Z. V. On the Weierstrass-Mandelbrot Fractal Function, Proc. R. Soc., A370. 1980. P. 459–484.

12. Останин С.А. Генератор фрактального шума произвольной размерности //   Журнал радиоэлектроники: электронный журнал. 2012. №8. URL: http://jre.cplire.ru/jre/aug12/2/text.html