"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 2, 1999

оглавление

дискуссия

ВОЗБУЖДЕНИЕ ПОЛЕМ ПЛОСКОЙ ЭЛЕКТРОМАГНИТНОЙ ВОЛНЫ

ПРОВОДЯЩЕГО ЦИЛИНДРА В СЛОИСТОЙ ЗЕМЛЕ

В.С. Семенов, А.В. Неведомский,  В.Г. Дыбовский
Сибирский физико-технический институт (СФТИ) при Томском государственном университете

Получена 9 февраля 1999 г.

В настоящей статье приведено приближенное решение задачи о расчете вторичного поля от проводящего бесконечно-длинного цилиндра, расположенного в плоскослоистой земле. Решение получено с использованием методов криволинейных координат и функции источника в виде двойных рядов по функциям Бесселя. Результаты численных расчетов структуры рассеянных полей получены с учетом влияния границ раздела, электрических параметров слоев и частоты.

Работы посвященные задачам дифракции электромагнитных волн на цилиндрических телах, расположенных в проводящем полупространстве или в горизонтально-слоистой проводящей среде, можно условно разделить на две группы. К первой, наиболее многочисленной группе, относятся работы, в которых задачи дифракции электромагнитных волн на цилиндрических телах рассматриваются в строгой постановке[1-5]. Такие задачи решаются при помощи метода интегральных уравнений численным путем. Недостатком метода интегральных уравнений, кроме трудности быстрого и достаточно точного вычисления функции Грина, является довольно сложный путь численного решения.

Ко второй группе относятся работы, в которых в явном виде получены приближенные выражения для составляющих электромагнитного поля цилиндра, расположенного в проводящем полупространстве [6-10]. К этой же группе работ относится и настоящая статья, в которой получены относительно простые выражения для компонент поля цилиндра в слоистой среде в явном виде, что позволило значительно расширить возможности анализа теоретических моделей.

Электродинамическая задача формулируется следующим образом: в нижнем слое среды на расстоянии z=-z₁ от верхней границы находится идеально проводящий цилиндр радиуса a с образующей параллельно оси x (Рис.1). Под воздействием падающей плоской электромагнитной волны ТМ - типа на поверхности цилиндра будут индуцироватся продольные токи. Требуется определить рассеянное поле цилиндра в воздухе [9,10]. Полное поле будет складываться из первичного и дифрагированного. Дифрагированное поле цилиндра можно выразить через x-ю составляющую векторного потенциала:

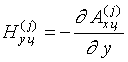,  , ,  (1)

_- абсолютная магнитная проницаемость слоя j.

Выражение для векторного потенциала ищется с помощью метода функции источника, сущность которого заключается в том, что под действием падающей плоской волны на поверхности цилиндра наводятся индуцированные токи плотностью в направлении образующей цилиндра (оси x). Электромагнитное поле цилиндра будет складываться из полей, создаваемых отдельными линейными токами.

В свою очередь распределение линейных токов индукции на поверхности цилиндра находится в результате использования приближенного выражения для вектор - потенциала линейного тока в слоистой среде [11]:

при ,  , при (2)

где (3)

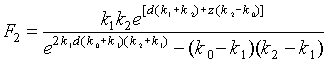(4)

волновое число j слоя среды,

Здесь F₁ и F₂ -функции, приближенно учитывающие влияние границ раздела.

K₀ - функция Макдональда нулевого порядка.

Приближенное выражение (2) находятся методом криволинейных координат [12].

Используя эти выражения, потенциал поля цилиндра при помощи функции распределения линейных токов индукции можно представить в виде:

(5)

Применением граничного условия на поверхности цилиндра решение сводится к линейному интегральному уравнению Фредгольма первого рода относительно плотности тока:

(6)

- коэффициент прохождения.

Здесь , , 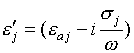- комплексная диэлектрическая проницаемость слоя,

- координаты точки наблюдения (М);

- координаты линейного тока (М₀);

- элемент длины контура L в точке М₀ (y₀ , z₀).

Применяя теорему сложения цилиндрических функций для и разлагая функцию плотности тока в ряд Фурье, интегральное уравнение (6) в цилиндрической системе координат с центром на оси цилиндра (рис.1) можно записать в виде:

(7)

В выражении (7) введены обозначения:

,   ,   ,

 ,

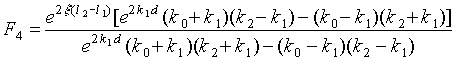  - - коэффициенты в разложении плотности тока в ряд Фурье.

Интеграл, стоящий в левой части выражения (7), представляет собой условие ортогональности экспоненциальных функций для полученного двойного ряда

Таким образом, члены двойного ряда при равны нулю, а в (7) останется только один член ряда с индексом

(8)

Применяя еще раз свойство ортогональности экспоненциальных функций и выполняя несложные преобразования, получим выражение для коэффициента b _n: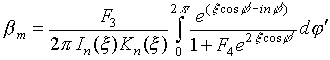

Теперь можно записать выражение для плотности тока на поверхности цилиндра:

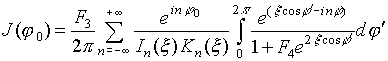 , (9)

Зная распределение тока на цилиндре, можно найти вектор - потенциал поля цилиндра в воздухе, в виде двойного ряда по модифицированным функциям Бесселя:

(10)

- число Неймана.

Используя соотношения (1), можно записать выражение для составляющих поля цилиндра в воздухе:

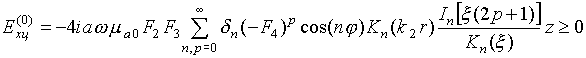
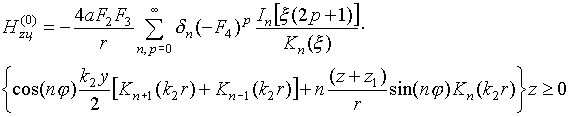(11)

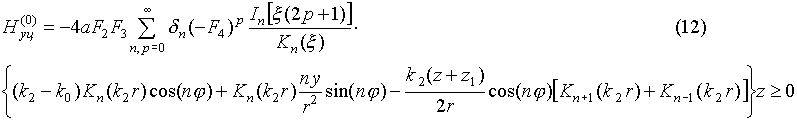
2. Результаты численных исследований.

На рис. 2-9 приведены результаты численных расчетов структуры электромагнитного поля цилиндра с учетом влияния границ раздела, электрических параметров слоев и частоты. Вид кривых на этих рисунках характеризуют структуру поля при перемещении точки наблюдения в плоскости перпендикулярной оси цилиндра на высоте z от поверхности земли. По оси абсцисс отложено относительное расстояние (y/h) вдоль поверхности земли, где рис.1.

На рис.2 - 4 показано поведение составляющих поля с изменением проводимости среды, окружающей цилиндр. При увеличении проводимости максимальные значения модулей компонент поля резко убывают. Менее интенсивно уменьшается вертикальная составляющая магнитного поля. Местоположение максимумов смещается к центру. О глубине залегания цилиндра можно судить по расстоянию между минимумом и максимумом при невысокой проводимости среды (рис.2). С увеличением проводимости среды необходимо вносить поправки на найденное значение глубины залегания.

На рис. 4 показано поведение горизонтальной электрической составляющей поля цилиндра. Для нее характерно еще более плавное изменение амплитудно - фазовых характеристик при перемещении над цилиндром, чем для H_y. По максимуму можно определить местоположение оси цилиндра.

Перейдем к исследованию частотной зависимости магнитного поля цилиндра. Величина уменьшается и местоположение _max. смещается к центру с ростом частоты (рис. 5). Фаза H_z имеет скачок на 180 ° над осью цилиндра и далее почти постоянна с изменением расстояния. Амплитуда горизонтальной компоненты магнитного поля цилиндра также уменьшается с ростом частоты, а фазовые кривые почти сохраняют свой вид для любой частоты. Как видно из рис. 5-6 с увеличением частоты возрастает погрешность определения глубины залегания цилиндра и более сильно для горизонтальной составляющей.

На  рис. 7-9 показаны зависимости составляющих электромагнитного поля цилиндра от его радиуса. Как видно из этих рисунков, увеличение радиуса цилиндра приводит, в основном, к возрастанию амплитуды составляющих. При этом фаза изменяется весьма незначительно. Каких либо характерных изменений в структуре компонент поля, по которым можно было бы осуществить классификацию цилиндров в зависимости от величины их радиуса, не наблюдается. Если цилиндр заменить линейным переменным током соответствующей амплитуды, расположенным на его оси, то увеличение радиуса цилиндра будет эквивалентно не только увеличению амплитуды переменного тока, но и перемещению его местоположения вверх от геометрической оси цилиндра. Данный эффект объясняется неравномерностью распределения тока по поверхности цилиндра. Действительно, при больших радиусах цилиндра со стороны падения возбуждающего поля будут наводится индукционные токи большей амплитуды, чем на противоположной «теневой »стороне, где токи наводятся за счет дифракции первичного поля. В результате, электрическая ось цилиндра смещается вверх от его геометрической оси.

1. Разработана методика приближенного решения задачи дифракции плоской электромагнитной волны на проводящем цилиндре в горизонтально слоистой среде, которая представляет собой сочетание метода криволинейных координат и метода функции источника. Применение этой методики позволило получить в явном виде выражения для составляющих поля цилиндра.
2. На основе полученного решения проведены численные расчеты структуры вторичных электромагнитных полей с учетом влияния границ раздела, электрических параметров слоев и частоты.
3. В результате анализа электромагнитного поля цилиндра отмечено, что увеличение проводимости слоев и частоты приводит к деформации составляющих поля цилиндра, при этом в меньшей степени подвержена изменениям вертикальная компонента.
4. Показано, что определение координат цилиндра с использованием вертикальной составляющей его магнитное поле является наиболее точным и простым способом.
5. Осуществить классификацию цилиндров в зависимости от величины их радиуса не представляется возможным, так как в структуре электромагнитного поля цилиндра не происходит при этом каких либо характерных изменений.

 Литература

1. Дмитриев В.И. Дифракция произвольного электромагнитного поля на цилиндрических телах. В сб. Вычислительные методы и программирование. Изд-во ВЦ МГУ, 1966, вып. 5, с. 253-259.
2. Захаров Е.В. К дифракции плоского электромагнитного поля на однородном цилиндрическом теле, погруженном в слоистую среду. Изв. АН СССР, Физика земли, 1969, №1, с. 57-62
3. Кауфман А.А., Табаровский Л.А., Терентьев С.А. Электромагнитное поле эллиптического цилиндра в горизонтально-слоистой среде. Изд-во СО АН СССР, институт геологии и геофизики, 1971, с. 110
4. Кауфман А.А., Табаровский Л.А., Терентьев С.А. К теории индуктивной рудной электроразведки в горизонтально неоднородных средах. Изд-во СО АН СССР, Геология и геофизика, 1972, №10, с. 96-104.
5. Табаровский Л.А. Применение метода интегральных уравнений в задачах геоэлектрики. Изд-во СО АН СССР, Наука, институт геологии и геофизики, 1975, вып.260, с.142.
6. Никитина В.Н. Об аномалиях переменных магнитных полей над цилиндрическими неоднородностями. Изд-во СО АН СССР, труды геофизического, 1956, №32, с.62-93.
7. Сикорский В.А. Плоская электромагнитная волна над цилиндром в проводящем полупространстве. Изв. вузов, Геология и разведка, 1969, №1, с. 106-111.
8. Дьконов Б.П. Дифракция электромагнитных волн на круглом цилиндре в однородном полупространстве. Изв. АН СССР, сер. геофизическая, 1959, №9, с. 1332-1343.
9. Неведомский А.В. Дифракция плоской электромагнитной волны на проводящем цилиндре в горизонтально-слоистой среде. Изв. вузов, Физика, деп., 1978, №11, с. 118.
10. Семенов В.С. Электромагнитное зондирование подстилающей поверхности и верхнего слоя грунта с целью их контроля и диагностики. Изв. вузов, Физика, 1998, №8 с. 62-75.
11. Неведомский А.В. О приближенном расчете поля линейного переменного тока в слоистой среде. Изв. вузов, Физика, деп., 1978, №10, с. 159.
12. Кулько В.Ф., Михайловский В.П. Электромагнитное поле в слоистых проводящих средах. Киев, Наукова думка, 1967, с. 125-142.

Рис. 1

a=0,2 m; z₁=2,0 m; z=0,5 m; d=0 m; f= 0,3 МГц.

Рис. 2.  Поведение вертикальной составляющей магнитного поля цилиндра при изменении электрических параметров среды.

1 - e _1,2 = 10; s _1,2 = 10^-3 См/м;

2 - e _1,2 = 20; s _1,2 = 10^-2 См/м;

3 - e _1,2 = 30; s _1,2 = 10^-1 См/м;

a=0,2 м; z₁=2,0 м; z=0,5 м; d=0,0 м; f= 0,3 МГц.

Рис. 3. Поведение горизонтальной составляющей магнитного поля цилиндра при изменении электрических параметров среды.

1 - e _1,2 = 10; s _1,2 = 10^-3 См/м;

2 - e _1,2 = 20; s _1,2 = 10^-2 См/м;

3 - e _1,2 = 30; s _1,2 = 10^-1 См/м;

a=0,2 м; z₁=2,0 м; z=0,5 м; d=0,0 м; f= 0,3 МГц.

Рис. 4. Поведение электрической составляющей поля цилиндра при изменении электрических параметров среды.

1 - e _1,2 = 10; s _1,2 = 10^-3 См/м;

2 - e _1,2 = 20; s _1,2 = 10^-2 См/м;

3 - e _1,2 = 30; s _1,2 = 10^-1 См/м;

e ₁ = 30; s ₁= 10^-1 См/м; e ₂ = 20; s ₂ = 10^-2 См/м;

Рис. 5. Частотная зависимость вертикальной составляющей магнитного поля цилиндра.

1 - f = 0,15 МГц

2 - f = 0,3 МГц

3 - f = 0,5 МГц

e ₁ = 30; s ₁= 10^-1 См/м; e ₂ = 20; s ₂ = 10^-2 См/м;

Рис. 6.  Частотная зависимость горизонтальной составляющей магнитного поля цилиндра.

1 - f = 0,15 МГц

2 - f = 0,3 МГц

3 - f = 0,5 МГц

Рис. 7. Поведение вертикальной составляющей магнитного поля с изменением радиуса цилиндра.

1 - a = 10^-2 м; 3 - a = 0,2 м;

2 - a = 2,5· 10^-2 м; 4 - a = 0,4 м;

Рис. 8.  Поведение горизонтальной составляющей магнитного

поля с изменением радиуса цилиндра

1 - a = 10^-2 м;

2 - a = 10^-1 м;

3 - a = 0,4 м;

e ₁ = 30; s ₁= 10^-1 См/м; e ₂ = 20; s ₂ = 10^-2 См/м;

Рис. 9. Зависимость электрической составляющей поля от радиуса цилиндра.

1 - a = 10^-2 м;

2 - a = 10^-1 м;

3 - a = 0,4 м;

Авторы:

Семенов В.С. - д. т. н., профессор, зав. отд. СФТИ

Дыбовский Виктор Геннадьевич - к. ф.-м. н., ст. н. с. СФТИ, e-mail: dybovsky@ic.tsu.ru

оглавление

дискуссия