|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 2, 1999 | |
В.Н. Корниенко
Институт радиотехники и
электроники РАН
Получена 17 февраля 1999 г.
В работе описана вычислительная схема, позволяющая учесть потери энергии на электромагнитное излучение уединенным диполем-ротатором. Показано, что частота вращения ротатора обратно пропорциональна квадратному корню от времени.
Для решения нестационарных задач вакуумной электроники к настоящему моменту разработано большое количество численных алгоритмов. В связи с увеличением вычислительных ресурсов компьютеров все большее распространение получают прямые методы решения, основанные на непосредственном решении уравнений Максвелла.
Характерной особенностью задач вакуумной электроники является то, что в качестве активной среды выступает поток заряженных частиц, который в некотором приближении можно рассматривать как непрерывную среду. В этом случае коллективные эффекты, связанные со взаимодействием электронов потока, преобладают, в частности, над процессами, вызванными самовоздействием заряженных частиц.
В последнее время с целью выяснения возможности использования в качестве источников микроволнового излучения изучаются дискретные активные среды, состоящие из локализованных элементов [1]. При моделировании таких сред становится необходимым непосредственный учет радиационных потерь каждого элемента за счет самовоздействия.
В представляемой работе описана вычислительная схема, позволяющая учесть радиационные потери для случая, когда в качестве элемента дискретной среды взят жесткий диполь-ротатор.
Рассмотрим жесткий ротатор в виде двух сосредоточенных масс, расположенных на некотором расстоянии друг относительно друга и соединенных безмассовым стрежнем. Пусть через центр стержня проходит ось вращения ротатора. Образуем электрический диполь, поместив на массы заряды противоположного знака.
Если такой диполь-ротатор обладает некоторой начальной скоростью вращения, то он будет излучать электромагнитное поле, причем поле излучения будет носить дипольный характер. В результате потери механической энергии ротатора на излучение, его частота вращения со временем будет уменьшаться. Из общих соображений следует, что зависимость частоты от времени будет описываться монотонной убывающей функцией.
Для определения вида зависимости частоты вращения от времени используем следующую вычислительную схему.
Предположив, что основная часть механической энергии переходит в энергию дипольного излучения, мощность потерь для диполя-ротатора можно записать следующим образом [2]:
(1) 
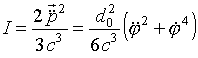
где 
-
модуль дипольного момента ротатора, 
- угол вращения.
Таким образом, временная производная механической энергии диполя-ротатора будет равна выражению (1), взятому с обратным знаком:
(2) 
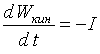
Запишем выражение (2) в конечных разностях,
задавая шаг по времени, равный 
, причем правую часть в (2) будем
брать в момент времени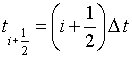 
, где i - номер текущего временного
шага:
(3)
где 
- момент
инерции ротатора,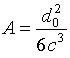 
.
Выражение (3) можно разрешить относительно 
, используя
метод итераций.
Учитывая, что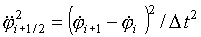 
можно записать:
(4) 
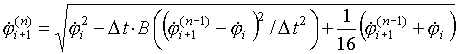
где верхний индекс (n) обозначает номер
итерации, 
.
Значение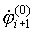 
полагается равным значению частоты вращения на
текущем временном шаге:
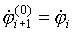
Процесс итераций заканчивается при выполнении условия
где 
-заранее заданная точность.
Представленная схема является условно устойчивой: за один шаг по времени относительное изменение энергии ротатора не должно превышать нескольких процентов.
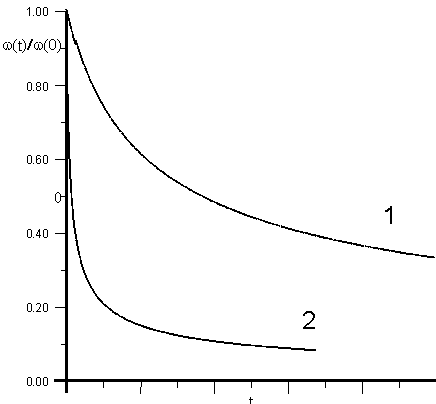
Рис.1. Изменение частоты вращения ротатора со временем: дипольный момент ротатора в случае кривой 1 меньше, чем для случая 2.
На рис.1. показаны зависимости частоты вращения диполя ротатора от времени для различных значений модуля дипольного момента. Полученные кривые достаточно хорошо аппроксимируются функцией вида:
,
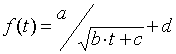коэффициенты 
которой зависят от момента инерции
ротатора и его дипольного момента.
ЛИТЕРАТУРА.
1. А.В. Корженевский, В.Н. Корниенко, В.А. Черепенин // Радиотехника и Электроника, 1998, т. 43, № 4, С. 1-6.
2. М.М. Бредов, В.В. Румянцев, И.Н. Топтыгин. Классическая электродинамика. М.: Наука, 1985 г., 400 с.
Автор: Корниенко Владимир Николаевич, korn@mail.cplire.ru
 |
 |