| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 1, 2000 |
ПРИМЕНЕНИЕ РЕЗОНАТОРА ДЛЯ ДИАГНОСТИКИ НЕОДНОРОДНОСТЕЙ ПРОВОДИМОСТИ ПОЛУПРОВОДНИКОВЫХ ПЛАСТИН
О.Г.Кошелев, Е.А.Форш,
Физический факультет Московского
Государственного университета им. М.В.
Ломоносова
Получена 27 января 2000 г.
Рассмотрен метод определения зависимости проводимости высокоомной полупроводниковой пластины от расстояния до ее поверхности. Расчеты на компьютере в одномерном приближении показали, что эта обратная задача может быть решена путем измерений добротностей открытого конфокального резонатора. Эти измерения должны проводиться на нескольких частотах при четырех положениях пластины в области перетяжки пучка в резонаторе.
1. Введение
Как известно, проводимость полупроводниковых пластин, используемых в различных приборах, обычно неоднородна. Эти неоднородности различаются по размерам, форме и причинам их образования. В объеме исходных пластин наблюдаются случайные флуктуации проводимости, имеющие как микроскопические, так и макроскопические размеры. Последние представляют собой в основном примесные облака, либо протяженные слои - страты [1]. При изготовлении ряда полупроводниковых приборов вблизи поверхности пластины путем диффузии, эпитаксии или ионной имплантации формируют тонкий (~ 0.1-10 мкм) сильно легированный слой. Параметры этих слоев также могут флуктуировать вследствие случайных изменений условий их получения. Работа большинства полупроводниковых приборов основана на неравновесной проводимости, т.е. на инжекции, диффузии, дрейфе и рекомбинации неравновесных носителей тока. Величина и характер распределения неравновесных носителей заряда меняются в широких пределах в зависимости от условий их генерации, типа примесных центров, их концентрации в объеме и на поверхности пластины. Исследование этих неоднородностей имеет важное значение для изучения различных физических процессов, а также для увеличения эффективности полупроводниковых приборов и уменьшения разброса их параметров.
Для определения профиля проводимости по толщине сильно легированных слоев на поверхности п/п пластин были разработаны бесконтактные методы, основанные на измерении зависимостей коэффициентов отражения и пропускания от длины волны
(l ) в ИК области (см., например, [2-6]). Однако эти методы не применимы для слабо легированных полупроводников. В рамках модели Друде коэффициент поглощения на свободных носителях пропорционален (1+w 2t 2)-1, где w -угловая частота, t - время пробега свободных носителей. В случае кремния параметр w 2t 2 >>1 в ИК области, тогда как в СВЧ и миллиметровой областях он меньше 1. Поэтому для определения проводимости и ее неоднородностей слабо легированных пластин используются методы, основанные на взаимодействии с волнами этих диапазонов. В частности, для определения распределения проводимости по площади пластины были предложены методы, основанные на измерениях параметров СВЧ резонатора, нагруженного исследуемой пластиной [7-9]. При этом полупроводниковая пластина располагается между дном резонатора квазистатического типа и конусообразным штырем, либо она прижимается снаружи к отверстию в торцевой стенке резонатора. Калибровка установки производится с помощью набора эталонных образцов. Такие измерения позволяют определять усредненные по толщине пластины значения удельного сопротивления до 104 Ом см с погрешностью около 10%.В работе [10] предложен метод определения зависимости проводимости пластины от расстояния до ее поверхности, основанный на измерениях коэффициента отражения от структуры исследуемая пластина-воздушный промежуток-зеркало в миллиметровой и субмиллиметровой областях спектра. По оценкам, метод может быть использован для пластин кремния с r порядка десятков Ом.см толщиной в доли мм, широко используемых для изготовления полупроводниковых приборов. Для более высокоомных пластин, используемых, например, в качестве подложек для СВЧ интегральных схем и окон гиротронов, применение метода затруднено из-за малости изменений коэффициента отражения.
В настоящей работе предлагается метод восстановления зависимости проводимости от расстояния до поверхности высокоомной пластины, основанный на измерениях добротности открытого резонатора в миллиметровой и субмиллиметровой областях спектра.
2. Сущность метода.
Рассмотрим в одномерном приближении взаимодействие высокоомной полупроводниковой пластины толщины
L с электромагнитной (э.м.) волной миллиметрового и субмиллиметрового диапазонов. Будем считать, что ее поглощение в пластине мало, т.е.Здесь
N, c и a - вещественная, мнимая части показателя преломления и коэффициент поглощения пластины, х- координата в направлении, перпендикулярном поверхности пластины, х=0 соответствует середине пластины (см. рис. 1).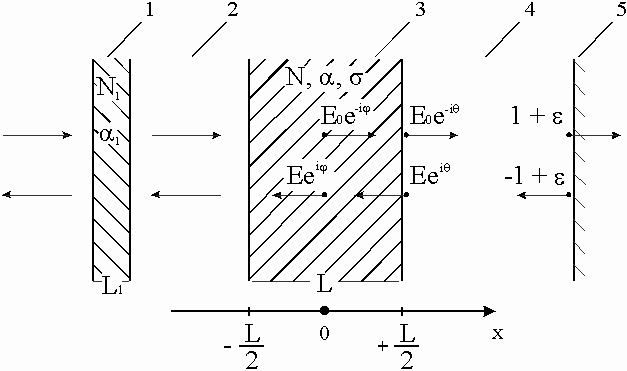
Рис.1. Принципиальная схема с основными обозначениями. 1-четверть-волновая диэлектрическая пластина, 2, 4-воздушные промежутки, 3-полупроводниковая пластина, 5-зеркало.
Пусть в пластине в противоположных направлениях перпендикулярно ее поверхностям распространяются плоские волны вида
Eexp[± i(kx+j )], где k=2p N/l , 2j -сдвиг фаз между волнами при x=0. В этом случае мощность P, поглощаемая пластиной единичной площади, может быть представлена в виде|
|
(4). |
Будем также считать, что поглощение происходит только на свободных носителях заряда, время свободного пробега которых постоянно, т.е.
t (х)=const |
(5). |
Тогда в рамках модели Друде для слабо поглощающего полупроводника
|
|
(6), |
где
Z - волновое сопротивление вакуума (Z=377 Ом), s - проводимость пластины. Благодаря условию (5) множитель (1+w 2t 2) можно вынести из под знака интеграла. Будем считать также, что оптическая толщина пластины кратна целому числу полуволн, т.е.|
l m=2LN/m=2LN/m |
(7), |
где
m=1, 2, 3,..., M. Тогда подстановка выражений (6) и (7) в (4) дает|
|
(8). |
Индекс
m при P и w здесь и далее у других величин означает, что соответствующая величина относится к случаю, когда l =l m. Из (8) видно, что алгебраические суммы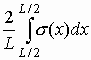 ,
,
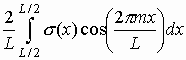 ,
, 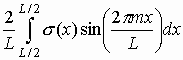 , т.е. коэффициентам разложения зависимости s
(х) в ряд Фурье.
, т.е. коэффициентам разложения зависимости s
(х) в ряд Фурье.
Таким образом обратная задача, состоящая в определении профиля проводимости полупроводниковой пластины по ее взаимодействию с э.м. волной, может быть решена однозначно в одномерном приближении, если параметры пластины удовлетворяют условиям (1)-(3), (5), (6). А именно, для этого нужно на длинах волн, удовлетворяющих условию (7), измерить значения поглощений пластины при четырех положениях в поле стоячей волны, для которых
|
j = 0, p /4, p /2, 3p /4 |
(9). |
По массиву таких данных можно вычислить коэффициенты разложения зависимости s
(х) в ряд Фурье и затем приближенно восстановить эту зависимость. Очевидно, что точность такой аппроксимации зависит от вида профиля проводимости и числа гармоник, на которых проводятся измерения.Для реализации этой задачи можно измерять поглощение пластины помещенной в середину открытого конфокального резонатора перпендикулярно его оси, т.е. в область перетяжки пучка, где фронты волны практически плоские, а диффракционные потери пренебрежимо малы при радиусе пучка W
0 всего в несколько длин волн [11].Приведем оценки, характеризующие выполнимость условий (1)-(3), (5) для высокоомного кремния n-типа в миллиметровом диапазоне волн. Например, если l
<1 см и удельное сопротивление r >100 Ом.см, то на основании данных работы [12] можно показать, что c /N<0,03, ê1-N /N0 ê <0,001 (N0 -показатель преломления чистого кремния). При этом a (l )L<0,13 для пластин толщиной менее 1 мм. С уменьшением l и с увеличением r условия (1)-(3) выполняются еще лучше. Условие (5) также хорошо выполняется, поскольку при r >100 Ом.см носители заряда рассеиваются практически только на колебаниях решетки (вклад рассеяния на примесных атомах составляет менее 0,2% [13]).3. Соотношения, связывающие профиль проводимости
с параметрами резонатора.Выразим коэффициенты разложения s
(x) в ряд Фурье (a0m, am, bm) через параметры, которые измеряются непосредственно. Вместо сдвига фаз 2j между интерферирующими волнами внутри пластины при x=0 введем сдвиг фаз 2q между ними снаружи, на поверхностях пластины (см. рис. 1), который измеряется по расстоянию между пластиной и зеркалом. Тогда можно показать, что при соблюдении перечисленных выше условий коэффициенты Фурье равны|
a0m=[NAm(0)+N-1(p /2)]Um |
(10), |
|
am=(-1)m[NAm(0)-N-1(p /2)]Um |
(11), |
|
bm=(-1)m[Am(p /4)-(3p /4)]Um |
(12), |
где
|
|
(13). |
А
m(q )-поглощаемая пластиной мощность, пронормированная на площадь и на интенсивность падающей волны. Соответственно, восстановленный профиль проводимости s ap(x) может быть представлен приближенно в виде ряда Фурье|
|
(14), |
где
|
|
(15). |
Здесь для повышения точности величина
a0 определяется путем усреднения значений a0m, поскольку они зависят от m при наличии неоднородностей проводимости.Следующей задачей является связать коэффициенты
Аm(q ) с добротностью резонатора. Общие соотношения, связывающие добротность резонатора с поглощением даже однородной пластины довольно громоздки (см., например, [14], [15]). Нас интересует случай, когда пластина находится в открытом конфокальном резонаторе в области перетяжки пучка э.м. волны, где фронты волны почти плоские. Поэтому для упрощения анализа взаимодействия волны с пластиной мы ограничились одномерным случаем. (Условия, при которых такое приближение допустимо, будут рассмотрены ниже). А именно, для расчета на ЭВМ поглощения неоднородной пластины здесь рассматривается одномерная модель резонансной системы, показанная на рис. 1. Она состоит из четвертьволновой диэлектрической пластины 1, воздушных зазоров 2, 4, полупроводниковой пластины 3 и зеркала 5. Удобство такой модели резонатора состоит в том, что его добротность, нагруженного неоднородной пластиной полупроводника, может быть легко вычислена на ЭВМ, например, с помощью реккурентных формул [16]. Если добротности нагруженного Qm(q ), и пустого Q0 резонатора удовлетворяют условиям Qm(q ), Q0>>1, то|
|
(16), |
где
|
|
(17). |
Здесь
N1, a 1, L1-показатель преломления, коэффициент поглощения и толщина пластины 1 (L1N1=l m/4), Lr- длина резонатора, соответствующая резонансу на длине волны l m, 2e -уменьшение амплитуды электрического поля волны при отражении от зеркала. Первое слагаемое в (17) определяет величину связи резонатора с трактом, второе и третье -потери в пустом резонаторе. Как видно, вариации величин N1, a 1, e и Lr позволяют моделировать резонаторы с разными параметрами и подбирать оптимальные условия для определения Аm(q ).Добротность резонатора определяется по изменению его длины, необходимой для уменьшения поглощения в 2 раза по сравнению с поглощением при резонансе (Эта методика, позволяющая определять добротность резонатора при фиксированной частоте, была предложена в работе [17]). В настоящей работе набор значений
Qm(q ) определялся путем компьютерного моделирования для пластин с заданными параметрами. При этом неоднородная пластина рассматривалась как ступенчатая структура, состоящая из большого числа (более 100) однородных слоев. Такое компьютерное моделирование позволило опробовать рассматриваемый метод для пластин и резонаторов с самыми различными параметрами и сравнивать восстановленные профили проводимости с исходными.4. Результаты и их обсуждение.
Анализ условий применимости и точноcти метода проводился применительно к пластинам высокоомного кремния (
N=3,4, t =2.10-13 с) с различными параметрами. Ниже приводятся результаты восстановления профиля проводимости с флуктуациями гауссовского типа для пластин толщиной L=1 мм. Аппроксимация проводилась рядом Фурье из 8 гармоник (M=8), что соответствует длинам волн от 6,8 мм до 0,85 мм.В качестве иллюстрации на рис. 2 приведены исходная (кривая 1) и восстановленные при различных условиях (кривые 2, 3) зависимости s
(x). Исходная зависимость соответствует проводимости, описываемой уравнениемгде s
v-1=20 kОм см, s f /s v=4, Lf /L=0,1; xf /L=-0,25. Кривая 2 вычислена по формулам (10)-(16) при точном соблюдении условий (7) и (9). Как видно, кривые 1 и 2 хорошо согласуются с точностью, определяемой числом гармоник Фурье ряда. Такое же согласие было получено при изменении s v на 3 порядка (в диапазоне s v-1 =0,1-100 кОм.см).
Рис.2. Исходная (1) и восстановленные (2,3) зависимости проводимости от х для пластины кремния. Кривая 1 соответствует s v-1=20 kОм см, s f/s v=4, L=1 мм, Lf/L=0,1, xf/L=-0,25. Кривые 2, 3 вычислены по формулам (10)-(16). Кривая 2 соответствует точному выполнению условия (9), кривая 3-смещению пластины от оптимального положения на D L=0,001L.
Однако реально из-за неизбежных экспериментальных ошибок условия (7) и (9) могут быть выполнены лишь приближенно. Поэтому были проведены дополнительные расчеты по оценке допустимых погрешностей. Кривая 3 на рис. 2 вычислена для случая, когда пластина смещена от оптимальных положений, соответствующих условию (9) на D
L=0,01L (D q @ 0,01 рад при m=1). Как видно, точность аппроксимации заметно снижается- максимальная относительная ошибка D s /s v @ 23%. Вычисленная по аналогичным кривым зависимость D s /s v от D L/L показана на рис. 3 кривой 1. Здесь же кривой 2 показана зависимость D s /s v от перекоса пластины на ± D L/L в пределах диаметра пучка. При радиусе пучка W0, равному 3l 1, перекос пластины f равен 0,025D L/L рад. Эти значения f отложены по верхней оси абсцисс. Как видно, для получения D s /s v @ 10% при L=1 мм допустимые значения D L и f составляют соответственно 0,5 мкм и 1,5.10-4 рад, т.е. для применения метода точность установки должна быть довольно высокой. Однако это препятствие является преодолимым, поскольку в настоящее время разработаны магнитострикционные прецезионные устройства позиционирования, обеспечивающие значительно большую точность (0,05 мкм и 5.10-6 рад [18])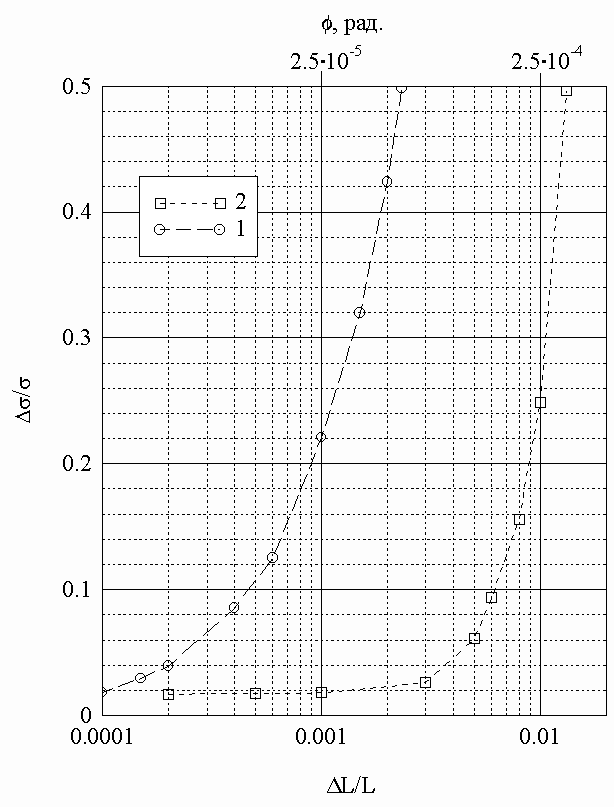
Рис.3. Зависимость максимальной погрешности D s /s v восстановленной зависимости s ap(X) от величины смещения D L/L пластины относительно оптимальных положений (кривая 1) и угла f между поверхностями пластины и фронтом волны при радиусе пучка W0=3l 1 (кривая 2). L=1 мм s v-1=2 kОм.см, ½ s f/s v -1½ <1, M=8.
На рис. 4 приведена вычисленная зависимость относительной ошибки от удельного сопротивления r пластины, соответствующая точности измерения добротности резонатора 0,5 %. Как видно, при изменении r в пределах двух порядков значение D s
/s v практически постоянно. При r <100 Ом.см точность резко снижается из-за низкой добротности резонатора. С увеличением точности определения добротности область малых значений D s /s v расширяется в сторону больших значений r .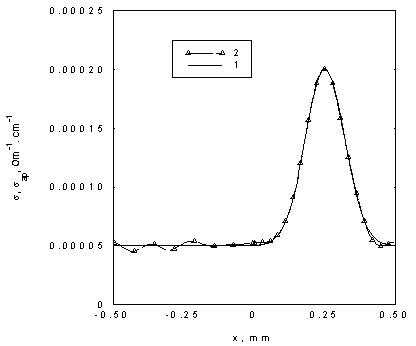
Рис.4. Исходная (1) и восстановленная (2) зависимости проводимости от х для пластины кремния. Кривая 1 соответствует xf/L=0,25, остальные параметры аналогичны кривой 1 рис. 2. Кривая 2 вычислена по формулам (10)-(16) при значениях добротностей резонатора, определенных с ошибкой 0,1%.
5. Заключение.
Рассмотрен бесконтактный неразрушающий метод определения зависимости проводимости высокоомной полупроводниковой пластины от расстояния до ее поверхности. Метод состоит в измерении добротности открытого резонатора при четырех положениях пластины в области перетяжки, при которых сдвиг фаз между интерферирующими волнами на поверхности пластины равен 0, p /2, p , 3p /2, и нескольких частотах, при которых толщина пластины кратна целому числу полуволн. Путем компьютерного моделирования в одномерном приближении метод опробован применительно к пластинам кремния. Проведен анализ влияния различных экспериментальных погрешностей на точность восстановления профиля проводимости.
Список литературы
Данилов Г.Н., Медведев Ю.В., Петров А.С. // ПТЭ, 1973, N. 3. С. 224.
Авторы: Кошелев Олег Григорьевич, e-mail: koshelev@scon282.phys.msu.su
Форш Елена Анатольевна