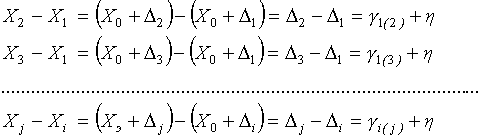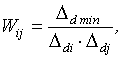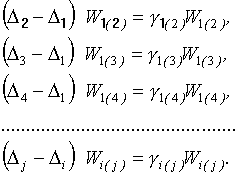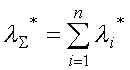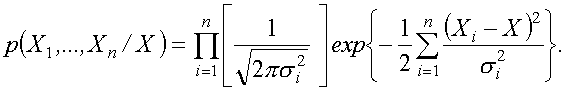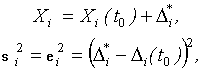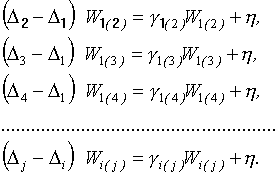c1.gif (954 bytes)

"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 1, 2002

оглавление

дискуссия

c2.gif (954 bytes)

 

Математический аппарат повышения метрологической автономности в системе единства измерений

 

Д.А. Безуглов,1) e-mail: bezuglovda@mail.ru,

 П.М. Поморцев,1)   В.Г. Ильин2)

 

1)Ростовский военный институт ракетных войск, г. Ростов-на-Дону.   

2)Ростовский институт сервиса Южно-российского государственного

университета экономики и сервиса, г. Ростов-на-Дону.                  

 

Получена 20 января 2002 г.

 

    Разработан универсальный математический аппарат  ведения групповых эталонов единиц физических величин, основанный на марковских моделях случайных процессов и методах обработки статистической информации. Исследованы новые методы повышения метрологической автономности в системе единства измерений.

 

1.   Введение

2.   Субоптимальная оценка единицы физической величины цифрового группового эталона

3.   Субоптимальная оценка единицы физической величины аналогового группового эталона

4.   Выводы

5.   Литература

 

 

1. Введение

 

        Современная теория единства измерений (теория воспроизведения единиц физических величин и передачи их размеров) наряду с теориями построения средств измерений и точности измерений традиционно является центральным разделом в теоретической метрологии. В совокупности решаемых задач, единство измерений можно охарактеризовать как состояние измерений, при котором их результаты выражены в узаконенных единицах, размеры которых в установленных пределах равны размерам воспроизведённых величин, а погрешности измерений известны с заданной точностью. Во многом единство измерений достигается путём точного воспроизведения, хранения установленных единиц физических величин, и передачи их размеров применяемым средствам измерений. Воспроизведение, хранение и передача размеров единиц осуществляется с помощью эталонов и образцовых средств измерений. Высшим звеном в метрологической цепи передачи размеров единиц физических величин являются эталоны.

        В настоящее время одним из перспективных направлений совершенствования средств измерений, предназначенных для хранения, воспроизведения и передачи размера единиц физических величин, является создание новых групповых эталонов, сформированных на базе группы хранителей единиц физических величин. Групповые эталоны разделяются на аналоговые и цифровые. Для цифровых групповых эталонов характерна высокая точность и быстродействие. В отличие от аналоговых, цифровые групповые эталоны имеют возможность автоматизации косвенных и совокупных измерений. Отличительными чертами цифровых групповых эталонов являются автоматическая калибровка и автоматическое введение поправок с целью уменьшения систематических погрешностей, отсутствие субъективных составляющих погрешностей и осреднение результатов измерений для уменьшения случайных погрешностей [1]. Эти обстоятельства позволяют исключить из уравнений взаимных сличений хранителей цифровых групповых эталонов влияние шумов измерений и использовать в обработке линейно инвариантные уравнения сличений, содержащих погрешности каждого хранителя группового эталона. В случае применения аналоговых групповых эталонов на фоне шумов измерений необходимо использовать информацию всех сличений.

    Выходные единицы группового эталона обычно являются аналитическими величинами, сформированными на ансамбле хранителей путем статистической обработки данных взаимных сличений между элементами группы. Поэтому стабильность цифрового группового хранителя определяется не только метрологическими характеристиками, но и эффективностью статистических методов обработки данных взаимных сличений. Таким образом, задача оценивания единицы физической величины группового эталона по результатам внутригрупповых сличений является актуальной, особенно в условиях перехода от традиционного принципа иерархии метрологического обеспечения к автономному. Под метрологической автономностью понимается свойство, заключающееся в способности поддерживать метрологические характеристики средств измерений и контроля, включая рабочие эталоны, без использования эталонных измерительных средств высшей точности, стоящих на более высоких ступенях передачи размера единицы физической величины.

          Целью данной работы является создание универсального математического аппарата  ведения групповых эталонов единиц физических величин, основанного на марковских моделях случайных процессов и методах обработки статистической информации, и разработка новых методов повышения метрологической автономности в системе единства измерений.

 

 

2. Субоптимальная оценка единицы физической

величины цифрового группового эталона

 

        Рассмотрим следующую математическую модель измерений. Пусть в момент времени t0 произвели сличение хранителей единицы физической величины группового эталона с исходным рабочим эталоном и получили следующие погрешности хранителей

                           (1)

где  - погрешность i – го хранителя группового эталона в момент времени t0; - значение единицы физической величины i – го хранителя группового эталона в момент времени t0;  – значение единицы физической величины исходного рабочего эталона; n – количество хранителей в групповом эталоне.

Тогда в момент времени t1, в условиях метрологической автономности, когда невозможно осуществить поверку хранителей группы по исходному рабочему эталону, проводятся сличения хранителей по схеме взаимных сличений. В общем случае, при количестве хранителей равном n, возможно провести  сличений. С учетом (1) запишем уравнения сличений, здесь и в дальнейшем опуская обозначения момента времени t1

(2)

где- соответственно значения погрешностей и значений единицы физической величины i,j – го хранителя группового эталона в момент времени t0;  - результат сличения в момент времени t0;  – гауссовские шумы сличений.

          Групповой эталон может быть сформирован как из равноточных, так и из разноточных средств измерений. Для случая неравноточных измерений введём матрицу весовых коэффициентов взаимных сличений [2]. Элементы этой матрицы (веса соответствующих сличений) определяются из выражения

                                                              (3)

где  - основная допустимая погрешность самого высокоточного хранителя группового эталона;  - соответственно основные допустимые погрешности i – го и j – го хранителя, участвующие в соответствующем сличении.

Использование цифровых групповых эталонов позволяет исключить из уравнений взаимных сличений хранителей (2) влияние шумов измерений и использовать в обработке линейно инвариантные уравнения сличений, содержащие погрешности каждого хранителя группового эталона

          Запишем уравнения (2) с учётом соответствующих весов сличений , умножив эти уравнения слева и справа на соответствующие весовые коэффициенты (3)

                                  (4)

В системе (4) из  уравнений линейно инвариантными являются только n – 1. Выбрав из (4) n – 1 уравнений с большими весовыми коэффициентами, содержащих погрешности каждого хранителя группового эталона, необходимо дополнить получившуюся систему выражением для суммарной погрешности группового эталона , добившись тем самым вынужденной инвариантности системы из n уравнений.

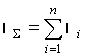            ,                                                             (5)

где –погрешность i – го хранителя группового эталона на момент сличений t1.

Однако, ввиду того, что величины , невозможно определить без наличия исходного рабочего эталона, оценки погрешностей хранителей  определим на основе математического аппарата марковских случайных процессов для оценки максимального межповерочного интервала группового эталона [3].

Предположим, что значения погрешности единиц физических величин  , являются марковскими, описываются гауссовской плотностью вероятностью и следующим дифференциальным уравнением

.

Задачу по определению межповерочного интервала Тn для средств измерений, хранящих единицу физической величины в составе группового эталона, будем  решать на основе уравнения Колмогорова-Фокера-Планка для случайных процессов. Прямое уравнение Колмогорова для n мер запишем в следующем виде

        ,

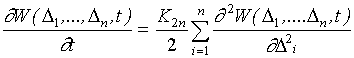где - плотность вероятности попадания значений погрешности физической величины в доверительный интервал ; -коэффициент диффузии для группового эталона.

Решением этого уравнения является функция [3]

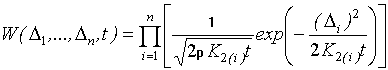, (6)

где - коэффициент диффузии i-того средства измерения группового эталона;

Для решения поставленной задачи необходимо найти плотность распределения действительного значения погрешности группового эталона , т.е. .

        .

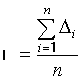Выражение для  может быть получено в результате интегрирования промежуточной функции [3]

  ,

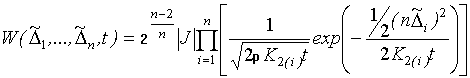полученной путем замены переменных в уравнении (6), здесь

           ,

          ,

          ,

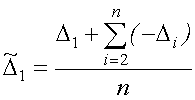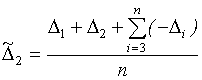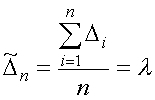J- якобиан преобразования

            .

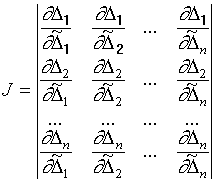Общее уравнение для  примет вид

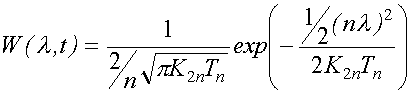    .      (7)

При заданном доверительном интервале  и доверительной вероятности , учитывая выражение (7) и выражение для вероятности попадания значения случайной величины в какой - либо конечный интервал, можно записать

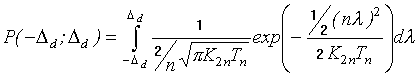. (8)

Путем замены переменных, приводим подынтегральное выражение в формуле (8) к виду функции  ошибок  (функции Лапласа), значение которой сведены в таблицы [4]

        =.

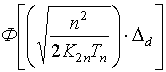Общее решение уравнения для определения межповерочного интервала Тn для n средств измерений, входящих в  групповой эталон, в этом случае примет вид

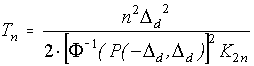        ,             (9)

где  функция, обратная

Решив подобную задачу для единичного средства измерений, получим выражение для межповерочного интервала хранителя группового эталона

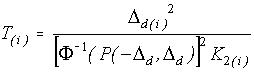        ,            (10)

где Т(i) - межповерочный интервал данного хранителя.

Выражение для оценки погрешностей хранителей  группового эталона примет вид

        ,        (11)

где t1- момент времени внутригрупповых сличений группового эталона (год);

Выражение для определения коэффициента диффузии i-ого хранителя группового эталона  имеет вид

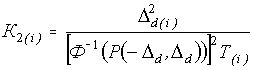         .        (12)

Таким образом, воспользовавшись (5,11,12), определим оценку суммарной погрешности группового эталона

                                                      (13)

С учётом (4) запишем систему из n уравнений в матричном виде

            ,                                                (14)

где

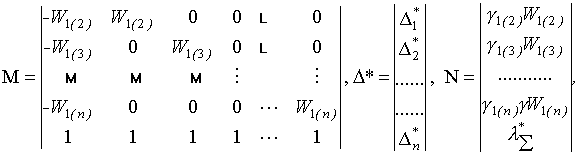
где  - оценки основной погрешности i–тых хранителей группового эталона, .

Матрицу оценок  основных погрешностей хранителей группового эталона в момент времени t1 находим из уравнения

         .                                                  (15)

Обратная матрица коэффициентов системы (15) принимает вид

   .

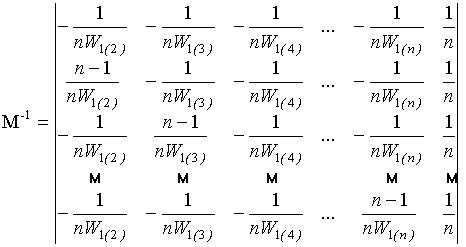Оценку значения единицы физической величины группового эталона по результатам взаимных сличений получим по критерию максимального правдоподобия.

Пусть действительное значение единицы физической величины i-го хранителя в групповом эталоне Xi подчиняется гауссовскому закону, тогда функция правдоподобия может быть записана в виде

        ,

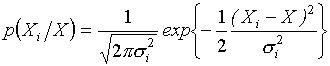где X - действительное значение единицы физической величины группового эталона;  - дисперсия Xi.

В силу независимости погрешностей функция правдоподобия для группового эталона запишется в виде

(16)

Уравнение оптимальной оценки значения единицы физической величины группового эталона Хч по критерию максимального правдоподобия имеет вид [5]

        .

Запишем уравнение оценивания в общем виде, воспользовавшись необходимыми условиями экстремума

          

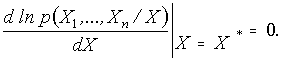
С учетом (16) уравнение оценивания примет вид

 

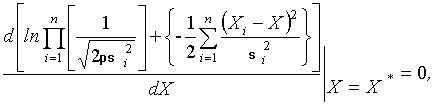
откуда

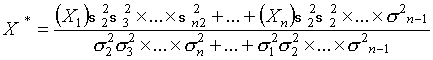.(17)

Так как в момент t1 Хi и  неизвестны, предлагается итоговое уравнение оценивания значения единицы физической величины записать с учётом статистических дисперсий , характеризующих изменение погрешности хранителей относительно предыдущей поверки Хi(t0) (1)

                                           (18)

где  - статистическая дисперсия погрешности i – го хранителя группового эталона.

Согласно (17, 18) выражение для максимально правдоподобной оценки значения единицы физической величины группового эталона примет вид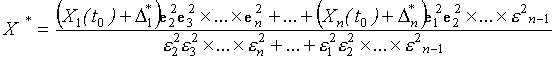.(19)

Методика формирования максимально правдоподобной оценки значения единицы физической величины группового эталона по результатам внутригрупповых сличений сводится к последовательности следующих операций:

1)    по результатам взаимных сличений записываем систему линейных уравнений (2);

2) определяем весовые коэффициенты взаимных сличений (3) и формируем матрицу весов;

3) записываем весовые уравнения внутригрупповых сличений (4);

4) рассчитываем коэффициенты диффузии для каждого хранителя (12);

5) рассчитываем оценки погрешностей хранителей (11);

6) определяем оценку суммарной погрешности группового эталона по (13);

7) согласно матрице весовых коэффициентов (3) выбираем n – 1 линейно независимых уравнений сличений, содержащих погрешности всех хранителей, и записываем вынужденно инвариантную систему из n уравнений в матричном виде (14) с учётом оценки суммарной погрешности группового эталона;

8) находим оценки основных погрешностей единиц физических величин хранителей группового эталона из уравнения (15);

9) рассчитываем значения статистических дисперсий погрешностей хранителей группового эталона (18);

10) максимально правдоподобную оценку значения единицы величины группового эталона по результатам внутригрупповых сличений находим из уравнения (19).

Пример. Имеется групповой эталон частоты, в состав которого входят пять низкочастотных прецизионных генераторов сигналов Г3-110 с погрешностью установки частоты = 3,0 * 10-7 (fnom = 1[МГц],    = 0,3[Гц]) По данным предыдущей поверки, проводимой в момент времени t0 и осуществляемой по исходным мерам (стандарт частоты и времени Ч1-74), абсолютные погрешности хранителей данного группового эталона имеют следующие значения:  = 0 [Гц], = 0,1 [Гц], = 0 [Гц], = -0,1[Гц], = 0,2[Гц]. Поскольку все хранители данного группового эталона одного класса точности, то весовые коэффициенты взаимных сличений одинаковы и равны . После проведения взаимных сличений хранителей получены следующие значения абсолютных разностей частот  = 0 [Гц],  = -0,5 [Гц], = -0,6 [Гц], = 0 [Гц]. Учитывая, что= 0,3[Гц], доверительная вероятность =0,997 и межповерочный интервал для каждого генератора Тi = 1 год,, коэффициенты диффузии для каждого хранителя группового эталона согласно (12) будут равны K(i) =0,01 [Гц2/год],. Сличения производятся через полгода со дня последней поверки (t1 = 0,5), из (11) получим значения оценок погрешностей хранителей  = 0,21[Гц],. Оценка суммарной погрешности группового эталона по (13) равна      = 1,05[Гц]. Вынуждено инвариантная система с учётом этой оценки примет вид

        .

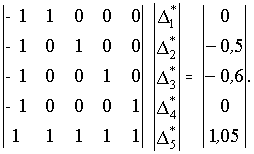Решив систему, получим оценки основных погрешностей группового эталона:= 0,43[Гц],=0,43[Гц], =-0,07[Гц],= -0,17[Гц],= 0,43[Гц]. Статистические дисперсии хранителей согласно (18) равны соответственно:    = 0,185[Гц2], = 0,109[Гц2], = 4,9 * 10-3[Гц2], = 4,9 * 10-3[Гц2], = 0,053[Гц2]. Из выражения (19) находим значение оценки единицы частоты, хранимой данным групповым эталоном,  = 999999,854[Гц] (= 1,46 ч10-7).

          Для апробации разработанной методики проводился натурный эксперимент по исследованию воспроизводимости единицы частоты групповым эталоном, групповой хранитель которого сформирован на базе четырёх аттестованных стандартов частоты и времени Ч1-74 [6]. Достоверность оценок значений основной погрешности по частоте определялась на основе сопоставления оценок, полученных по представленному выше алгоритму, с действительными значениями этого параметра, которые, в свою очередь, были получены в результате сличения хранителей группового эталона с образцовой мерой частоты, в качестве которой использовался водородный стандарт частоты Ч1-75.

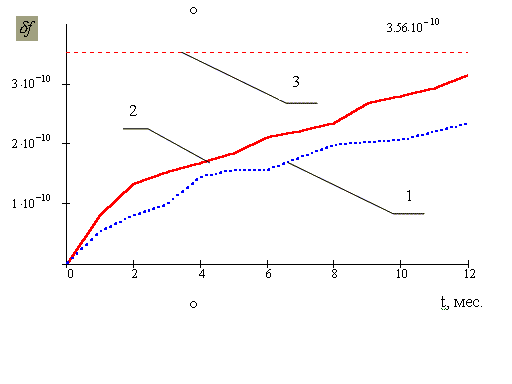
В результате проведённого натурного эксперимента установлено, что погрешность оценки действительного значения единицы частоты группового эталона, полученной по разработанному алгоритму на интервале времени 1 год, составила в среднем  ±4,6´10-11, что в семь раз меньше предельно допустимой погрешности. Результаты численного моделирования показали, что методическая погрешность, возникающая при использовании в группе как равноточных, так и разноточных хранителей, на порядок меньше допустимой. На рис. 1 представлен график годового изменения действительного значения основной относительной погрешности по частоте группового эталона определённого на основе сличений с водородным стандартом Ч1-75 (кривая 1), и максимально правдоподобных оценок этой погрешности (кривая 2) относительно основной предельно допустимой погрешности по частоте стандарта Ч1-74 (прямая 3).

 

1 – действительное значение;                            

2 – максимально правдоподобная оценка;        

3 – основное предельно допустимое значение.

Рис. 1. График изменения основной погрешности по частоте группового эталона

 

 

3. Субоптимальная оценка единицы физической

величины аналогового группового эталона

 

        Для аналоговых групповых эталонов уравнения внутригрупповых сличений хранителей примут вид

                            (20)

Применив критерий максимального правдоподобия, уравнение оптимальной оценки  примет вид

            .

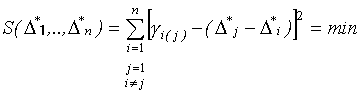          На основании теоремы о необходимых условиях экстремума следует, что эти значения удовлетворяют системе уравнений

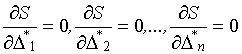              .                      (21)

В развёрнутом и общем виде система (21) примет вид

            ,         

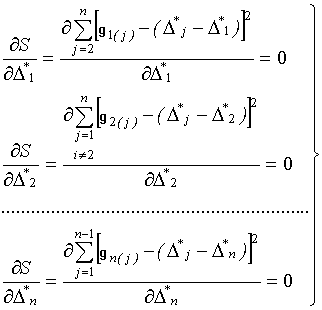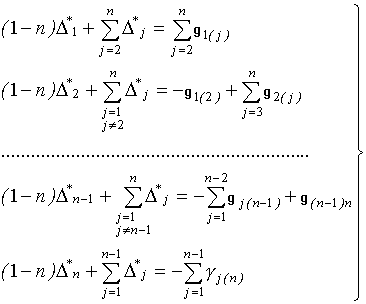              .(22)

Уравнения системы (22) не являются линейно инвариантными. Исключив из (22) n – ое уравнение с меньшим весовым коэффициентом Wi(j), необходимо дополнить получившуюся систему выражением для оценки суммарной погрешности группового эталона  (13), добившись тем самым вынужденной инвариантности системы из n(n-1)/2 уравнений.

          Запишем (22) c учётом (13) и весовых коэффициентов Wi(j), в матричном виде (14)

где

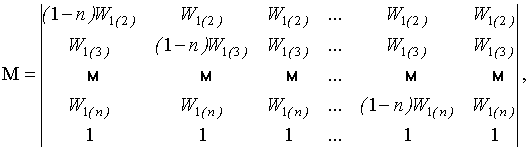
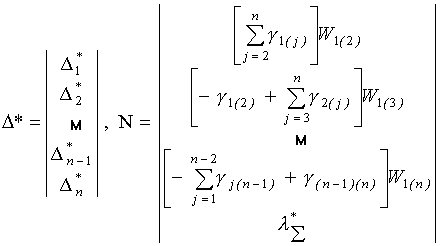
Матрицу оценок  основных погрешностей хранителей группового эталона в момент времени t1 находим из уравнения (15), в котором матрица М-1 принимает вид.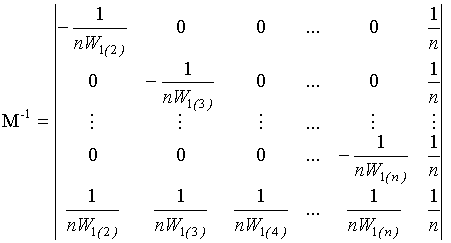

Оценку значения единицы физической величины группового эталона по результатам взаимных сличений получаем по критерию максимального правдоподобия (18, 19).

Пример. Имеется групповой эталон, в состав которого входят пять катушек сопротивления P321 одного класса точности 0,01 ( = 0,01), с номинальным значением сопротивления Rnom= 10[Ом]. По данным предыдущей поверки, проводимой в момент времени t0 и осуществляемой по исходным мерам (катушка сопротивления P321 I разряда), абсолютные погрешности хранителей данного группового эталона имеют следующие значения: = -4,0 * 10-5 [Ом]; = -5,0 * 10-5 [Ом]; = 1,0 * 10-5[ Ом]; = -3,0 * 10-5 [Ом]; = 2,0 * 10-5[Ом]. Поскольку все хранители данного группового эталона одного класса точности, то весовые коэффициенты взаимных сличений одинаковы и равны . После проведения взаимных сличений хранителей получены следующие значения абсолютных разностей сопротивлений = -3,0 * 10-5[Ом], = -2,0 * 10-3[Ом], = 2,7 * 10-5 [Ом], = 2,0 * 10-5[Ом], = -2,0 * 10-3[Ом], = -2,7 * 10-6 [Ом], =-9,5 * 10-6[Ом], = 2,0 * 10-3[Ом],  = 2,0 * 10-3[Ом],             = -6,8 * 10-4[Ом] Учитывая, что = 1,0 * 10-3[Ом], доверительная вероятность = 0,997 и межповерочный интервал для каждой катушки Т(i)=1год, , коэффициенты диффузии для каждого хранителя группового эталона согласно (12) будут равны K2(i) = 1,32 * 10-7[Ом2/год],.

Сличения производятся через год со дня последней поверки (t1 = 1), из (11) получим значения оценок погрешностей хранителей = 1,0 * 10-3 [Ом], . Оценка суммарной погрешности группового эталона по (13) равна  = 5,0 * 10-3 [Ом]. Вынуждено инвариантная система с учётом этой оценки примет вид

       

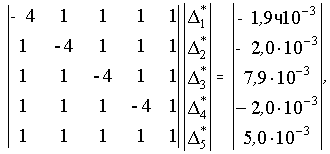
Решив систему, получим оценки основных погрешностей группового эталона:  = 1,4 *  10-3 [Ом], = 1,4 * 10-3[Ом],  = -5,9 * 10-3 [Ом], = 1,4 * 10-3 [Ом],  = 1,4 * 10-3 [Ом]. Статистические дисперсии хранителей согласно (18) равны соответственно: = 2,0 * 10-6 [Ом2], = 2,1 * 10-6 [Ом2],= 3,6 * 10-7[Ом2], = 2,1 * 10-6 [Ом2], = 1,9 * 10-6 [Ом2]. Из выражения (19) находим значение оценки единицы электрического сопротивления, хранимой данным групповым эталоном, R* = 10,00023 [Ом] (= 2,3 * 10-3).

 

 

4. Выводы

 

        Представленный в работе новый универсальный математический аппарат ведения аналоговых и цифровых групповых эталонов единиц физических величин, основанный на использовании марковских моделей случайных процессов и методов обработки статистической информации, позволяет существенно повысить автономность системы метрологического обеспечения в рамках современной теории единства измерений.

      Разработанные методы субоптимальной оценки единиц физических величин аналоговых и цифровых групповых эталонов позволяют в полной мере представить процесс воспроизведения, хранения и передачи размеров широкого класса единиц физических величин в условиях автономного метрологического обслуживания средств измерений и уменьшить экономические затраты при эксплуатации измерительной техники. В ходе решения поставленной задачи получены аналитические выражения для максимально правдоподобной оценки единицы физической величины цифрового и аналогового групповых эталонов, введены понятия матрицы весовых коэффициентов сличений и статистической дисперсии погрешности группового хранителя, представлен аналитический вид систем линейно инвариантных уравнений взаимных сличений хранителей цифровых и аналоговых групповых эталонов на фоне гауссовских шумов сличений, а также общий вид обратных матриц коэффициентов этих систем.

    Математическое моделирование разработанных алгоритмов обработки взаимных сличений хранителей аналоговых групповых эталонов показало, что данный математический аппарат может использоваться и применительно к цифровым групповым эталонам, но с большими аппаратными и временными затратами. В свою очередь применение алгоритмов сличений хранителей цифровых групповых эталонов позволяет достоверно оценивать значение единицы ФВ аналоговых групповых эталонов только в случаях, использования в групповом эталоне не более пяти хранителей. Это обусловлено недостаточным использованием информации n-1 уравнений сличений хранителей группового эталона.

    Важными достоинствами предложенных методов, по сравнению с существующими методами обработки внутригрупповых сличений хранителей группового эталона, являются наиболее рациональный коэффициент использования измерительной информации, уменьшение временных затрат на обработку результатов измерений, а также существенное повышение точности определения оценки единицы физической величины группового эталона в условиях метрологической автономности. Разработанный математический аппарат может найти применение при решении других важных вопросов метрологического обеспечения.

 

 

5. Литература

 

1.     Орнатский П.П. Автоматические измерения и приборы .– К.: Вища шк. Головное изд-во, 1986.

2.     Безуглов Д.А., Поморцев П.М. Максимально правдоподобная оценка единицы физической величины группового рабочего эталона по результатам внутригрупповых сличений // Измерительная техника. – 2001. –  № 1. – С.3.

3.     Безуглов Д.А., Поморцев П.М. Методика оценки межповерочного интервала групповой меры в цифровых измерительных системах // "Цифровая обработка сигналов и ее применение" DSPA 2000, Москва, 2000 г. т.2, с.132.

4.     ГОСТ 8.207-76. ГСИ. Прямые измерения с многократными наблюдениями. Методы обработки результатов наблюдений. Основные положения.

5.     Вентцель Е.С., Овчаров Л.А. Теория случайных процессов и её инженерные приложения. - М.: Наука, 1991.

6.     Безуглов Д.А., Поморцев П.М., и др. Патент на изобретение RU 2173856 С1 по заявке № 2000118339 от 10.07.2000. Способ оперативного воспроизведения единицы частоты групповой мерой в условиях полной автономности. 

 

оглавление

дискуссия