|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 1, 2003 |
|
ПОСТРОЕНИЕ ОБРАТИМЫХ ФУНКЦИОНАЛЬНЫХ МОДЕЛЕЙ ДИНАМИЧЕСКИХ СИСТЕМ С ДИСКРЕТНЫМ ВРЕМЕНЕМ ПО РЕАЛИЗАЦИЯМ ВХОДНОГО И ВЫХОДНОГО СИГНАЛОВ
Кисельман Б. А. , e-mail: kiselman@unc.sci-nnov.ru , Крылов В. В.
Нижегородский государственный технический университет,
каф. «Теория Цепей и Телекоммуникации».
Получена 10 января 2003 г.
В статье рассматриваются стационарные динамические системы дискретного времени с одним входом и одним выходом. Приведены основные модели таких систем (фильтры с конечной и бесконечной импульсными характеристиками, линейный предсказатель и дискретная система урысоновского типа). Все известные модели с конечной памятью по входу и выходу являются частными случаями введенной авторами обобщенной функциональной модели (ОФМ). Аддитивное представление последних наиболее значимо для их построения.
Представлен метод синтеза ОФМ по реализациям входного и выходного сигналов. Применение критерия наименьших квадратов для ошибки моделирования приводит к системе линейных алгебраических уравнений относительно коэффициентов ОФМ. Приведено условие обратимости ОФМ.
Основная проблема теории абстрактной реализации динамических систем была достаточно строго сформулирована Калманом: перейти от отображения вход-выход к уравнениям состояния. Эта задача успешно решена в классе линейных систем как с непрерывным, так и с дискретным временем [1]. Получен также ряд результатов и для нелинейных систем [2-4].
Целью данной статьи является представление метода синтеза нелинейных систем с дискретным временем непосредственно по реализациям входного и выходного сигналов с использованием стандартной структуры.
Далее будут рассмотрены стационарные системы дискретного времени с одним входом и одним выходом.
2. Основные методы синтеза систем с дискретным временем
Синтез стационарных систем дискретного времени может быть произведен с помощью сдвиговых автоматов [5]. Цифровая обработка сигналов для практических целей имеет в своем распоряжении такую модель линейной инерционной стационарной системы как БИХ-фильтр. Эта модель описывается следующим уравнением:
Частными случаями системы (1) являются трансверсальная структура (без обратной связи), соответствующая КИХ-фильтру (ak = 0 "k), и линейный предсказатель сигнала (bm = 0 "m). Если модель с дискретным временем описывается уравнением (1), то ее коэффициенты am и bk могут быть однозначно определены по известным векторам отсчетов входного {xn} и выходного {yn} сигналов методом наименьших квадратов. Далее будем для определенности считать, что xn, yn Î R.
При решении целого ряда задач часто бывает важно построить обратимую модель нелинейной инерционной системы, которую затем можно было бы использовать, например, для компенсации искажений, вносимых системой в обрабатываемый ею сигнал.
Наилучшим образом для решения этой задачи подходит урысоновская система с дискретным временем, описываемая уравнением
Покажем, что для нее существует точное обращение. Действительно, из уравнения (2) следует, что
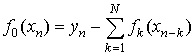 ,
,
откуда можно получить уравнение обращенной системы
Таким образом, если у f0 существует обратная функция, то модель (2) допускает точное обращение (3).
Анализ известных источников [6, 7] позволяет сделать вывод о том, что в настоящее время нелинейные инерционные системы с дискретным временем чаще всего моделируются соотношениями следующего вида:
где в качестве функций fk используются полиномы или сплайны 1-го порядка, коэффициенты которых вычисляются в ходе рекурсивных процедур типа метода градиентного спуска по известным отсчетам входного и выходного сигналов.
Резюмируя вышесказанное, можно сказать, что все перечисленные модели динамических систем дискретного времени являются частными случаями следующей модели:
которую назовем обобщенной функциональной моделью (ОФМ) динамической системы с конечной памятью (ДСКП). Важным является тот факт, что функция F(Xn, Yn), Xn = (xn, xn-1,…, xn-N), Yn = (yn-1, yn-2,…, yn-M), в рассмотренных частных случаях имеет аддитивное представление. В связи с этим возникает вопрос о возможности построения функции F (и, соответственно, ОФМ) по ее аддитивному разложению вида (4) и реализациям входного и выходного сигналов с помощью метода наименьших квадратов, что явилось бы обобщением этого метода для линейных систем вида (1).
3. Аддитивный синтез функции F по системе известных функций на основе отрезков входного и выходного сигналов
Поставим задачу синтеза ОФМ ДСКП на основе ее аддитивного представления:
где fk(X, Y) – известные функции (для краткости у X и Y опущен индекс n). Синтез функции F состоит в определении неизвестных коэффициентов разложения ak в (6). Пусть известны ее входной и выходной сигналы: xn и yn соответственно (n = 0,…, L). Если руководствоваться минимизацией квадрата ошибки моделирования, то можно показать (см. Приложение), что искомые коэффициенты ak являются решениями системы линейных алгебраических уравнений:
где a = (a0, a1,…, aK)T, Y = (Y0, Y1,…, YK)T,
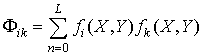 ,
,
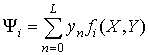 , i = 0, 1, …, K.
, i = 0, 1, …, K.
Таким образом, аддитивная структура (6) модели (5) может быть построена в ходе решения системы линейных алгебраических уравнений (7).
4. Обобщенный аддитивный синтез функции F
Рассмотрим более общий и практически важный случай построения функции F по ее аддитивному представлению (6), но уже с неизвестными функциями fk(X, Y). В остальном постановка задачи остается прежней.
Введем разложение
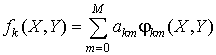 ,
,
где jkm(X,Y) – известные функции (примитивы разложения). Последнее понятие предполагает, что эти функции имеют более простой вид по сравнению с fk. Тогда функцию F можно искать в таком виде:
Аддитивное представление (8), очевидно, дает возможность найти коэффициенты akm методом наименьших квадратов. Действительно, если это двумерное представление развернуть в одномерное (перенумеровать систему примитивов представления jkm одним индексом), то получится разложение вида (6), коэффициенты которого можно найти, решив систему (7).
5. О возможности обращения дискретных систем
Как было показано в п. 1, нелинейная дискретная система урысоновского типа (2) допускает точное обращение (3). Очевидно, что этот результат можно обобщить, если структура системы (5) позволяет аддитивно разделить свои инерционную и безынерционную части. То есть, если система описывается уравнением
![]() ,
,
то у нее существует точное обращение
![]() ,
,
если f0 имеет обратную функцию.
По мнению авторов в данной работе новыми являются следующие положения и результаты.
· Введено понятие обобщенной функциональной модели динамической системы с дискретным временем и конечной памятью по входу и выходу (ОФМ ДСКП). Частные случаи этой модели – КИХ- и БИХ-фильтры, дискретные системы урысоновского типа и нелинейно-регрессионные системы.
· Указано условие, при котором ОФМ допускает точное обращение.
· Приведен метод синтеза ОФМ по реализациям входного и выходного сигналов. Использование критерия минимума квадратичной ошибки моделирования позволило найти системы линейных алгебраических уравнений относительно коэффициентов модели.
· Полученные результаты могут быть распространены на модели со многими входами и выходами с привлечением понятия связности систем.
Результаты настоящей работы могут быть использованы для эффективной реализации в системах цифровой обработки сигналов и цифрового управления нелинейными динамическими системами.
7.Приложение
Рассмотрим систему с дискретным временем, для которой известны реализации входного xn и выходного yn сигналов (n = 0, 1,…, L). Построим ее модель, описываемую уравнением
![]() ,
,
в котором функция F имеет представление
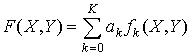 .
.
Найдем коэффициенты этой модели методом наименьших квадратов.
Квадратичная ошибка моделирования
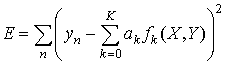 .
.
Коэффициенты ak можно найти, минимизируя Е. Необходимые условия существования минимума Е выглядят следующим образом:
 i
= 0, 1, …, K,
i
= 0, 1, …, K,
что приводит к системе уравнений
 , i
= 0, 1, …, K.
, i
= 0, 1, …, K.
Введя матрицу F и вектор Y со элементами
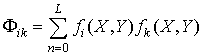 ,
, 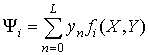 ,
i = 0, 1, …, K,
,
i = 0, 1, …, K,
получим матричное уравнение относительно вектора неизвестных коэффициентов:
![]() ,
,
где a = (a0, a1,…, aK)T, Y = (Y0, Y1,…, YK)T.
1. Калман Р., Фалб П., Арбиб М. Очерки по математической теории систем. М.: Мир, 1971.
2. Крылов В. В., Херманис Э. Х. Модели систем обработки сигналов. Рига.: Зинатне, 1981.
3. Крылов В. В. Построение моделей внутренней структуры динамических систем по входо-выходным соотношениям (теория абстрактной реализации). I. Обзор // АиТ. 1984. № 2. С. 5-19.
4. Крылов В. В. Построение моделей внутренней структуры динамических систем по входо-выходным соотношениям (теория абстрактной реализации). II. Обзор // АиТ. 1984. № 3. С. 5-19.
5. Фараджев Р. Г. Линейные последовательностные машины. М.: Советское радио, 1975.
6. Saleh A. A. M. Frequency-independent and frequency-dependent nonlinear models of TWT amplifiers // IEEE Trans. Commun. N. 1997. V. 29, P. 1715-1720.
7. Haykin S. Adaptive Filter Theory, NJ: Prentice-Hall, 1986.
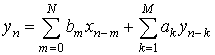
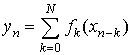
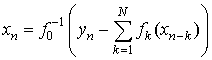 . (3)
. (3)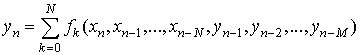 , (4)
, (4) . (8)
. (8)