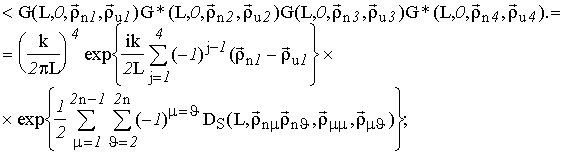|
|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 1, 2003 |
|
МАКРОПРОЕКТИРОВАНИЕ СИСТЕМ ТРАНСПОРТИРОВКИ
ЛАЗЕРНОЙ ЭНЕРГИИ
А.Н. Глушков, А.Л. Митрофанов, Т.Ю. Смагина.
E-mail: glushkov@trassa.org
ГУП «ГосНИИЛЦ РФ «Радуга», г.Радужный Владимирской обл.
Приводятся основные положения методического подхода определения основных параметров системы транспортировки лазерной энергии. Подход основан на максимизации коэффициента использования лазерной энергии при обеспечении заданной вероятности создания требуемого уровня энергии на приемнике излучения.
Начальным этапом разработки сложных систем является этап их проектирования на уровне формализации и исследования моделей систем в интересах обоснования их облика. В силу уникальности и слабопредсказуемости сложных систем [1] данная задача решается строго индивидуально. При этом большое количество параметров систем, а также их нелинейная взаимосвязь затрудняют использование оптимизационных методов, и процедура проектирования реализуется с помощью формальных и эвристических операций, упорядоченных отношениями обмена информацией и следования во времени [2]. Решение такой задачи можно охарактеризовать как макропроектирование.
Цель
настоящей работы состоит в разработке методического подхода к
макропроектированию лазерных систем, предназначенных для передачи энергии
излучения на удаленные объекты. Примером подобных систем являются системы
лазерной связи, локации, энергетические лазерные системы и др. Естественным
требованием к ним является обеспечение требуемой эффективности
функционирования, которая может быть охарактеризована вероятностью облучения
приемника излучения энергией E не ниже порогового уровня ![]() , а также коэффициентом
использования излучаемой энергии
, а также коэффициентом
использования излучаемой энергии ![]() .
.
Вероятность создания на приемнике лазерного излучения
требуемого уровня энергии ![]() определяется выражением:
определяется выражением:
![]() =
= 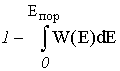 ,
,
где
![]() -
закон распределения флуктуаций энергии лазерного излучения в плоскости
приемника.
-
закон распределения флуктуаций энергии лазерного излучения в плоскости
приемника.
Функция
![]() может
быть представлена в виде частичной суммы ряда, представляющего разложение
плотности вероятности флуктуаций лазерной энергии по полиномам Лаггера
[3]:
может
быть представлена в виде частичной суммы ряда, представляющего разложение
плотности вероятности флуктуаций лазерной энергии по полиномам Лаггера
[3]:
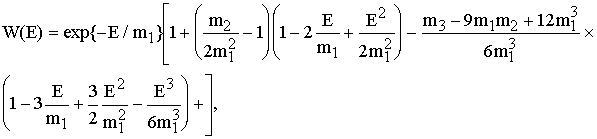
где
![]() -
моменты случайной величины E.
-
моменты случайной величины E.
В
этом случае выражение для ![]() при
при ![]() принимает вид:
принимает вид:
где
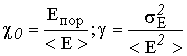 ;
;
 ;
;
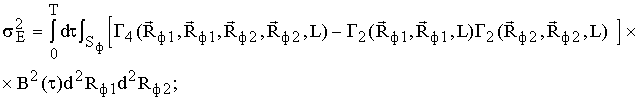
<E>,
![]() - математическое ожидание и дисперсия принимаемой энергии;
- математическое ожидание и дисперсия принимаемой энергии;
![]() и
и ![]() - функции
когерентности второго и четвертого порядков лазерного излучения в плоскости
приемника излучения;
- функции
когерентности второго и четвертого порядков лазерного излучения в плоскости
приемника излучения;
![]() - площадь приемника излучения;
- площадь приемника излучения;
![]() - временная корреляционная функция
флуктуаций лазерного излучения;
- временная корреляционная функция
флуктуаций лазерного излучения;
![]() - радиус-вектор в плоскости приемника;
- радиус-вектор в плоскости приемника;
Т - длительность передачи энергии.
Коэффициент использования излучаемой энергии ![]() характеризует
рациональность использования энергетического ресурса системы и определяется
отношением энергии, принятой приемным каналом системы E энергии,
излученной передатчиком
характеризует
рациональность использования энергетического ресурса системы и определяется
отношением энергии, принятой приемным каналом системы E энергии,
излученной передатчиком ![]() .
.
Представим величину ![]() в виде [4,5]:
в виде [4,5]:
![]() =
=![]() +
+![]() =
=![]() +D
+D![]() ,
,
где
 ;
;
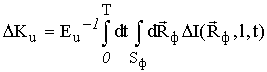 ;
;
скобки <×> - означают операцию статистического усреднения.
Здесь ![]() - распределение интенсивности излучения на
фотоприемнике, находящемся на расстоянии l за апертурой; t-
текущее время. Величина
- распределение интенсивности излучения на
фотоприемнике, находящемся на расстоянии l за апертурой; t-
текущее время. Величина ![]() =0, а её дисперсия определяется выражением:
=0, а её дисперсия определяется выражением:

Полагая временную зависимость поля во всех точках источника одинаковой [4], выражение для <Ku> при T>tk преобразуем к виду:
где tk - время корреляций флуктуаций поля;
PU - излучаемая мощность;
Здесь Т(×) - амплитудный коэффициент пропускания приемной оптики с фокусным расстоянием FL лазерного излучения с длиной волны l;
L - расстояние между излучающей и приемной апертурами;
![]() - суммарный и разностный радиус-векторы,
описывающие положение точек на излучающей и приемной апертурах;
- суммарный и разностный радиус-векторы,
описывающие положение точек на излучающей и приемной апертурах;
![]() - коэффициент, определяющий прозрачность
атмосферы;
- коэффициент, определяющий прозрачность
атмосферы;
![]() ;
;
![]() - функция когерентности второго порядка
источника излучения;
- функция когерентности второго порядка
источника излучения;
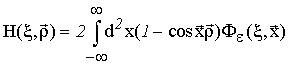 ;
;
![]() - пространственный спектр флуктуаций
диэлектрической проницаемости воздуха.
- пространственный спектр флуктуаций
диэлектрической проницаемости воздуха.
Рассмотрим световой пучок, у которого
где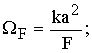
![]() - радиусы излучающей апертуры, кривизны
волнового фронта и пространственной когерентности пучка соответственно;
- радиусы излучающей апертуры, кривизны
волнового фронта и пространственной когерентности пучка соответственно;
U0 - амплитуда поля в центре излучающей апертуры; ![]() , s2 - математическое
ожидание и дисперсия ошибки нацеливания лазерного пучка на приемную апертуру.
, s2 - математическое
ожидание и дисперсия ошибки нацеливания лазерного пучка на приемную апертуру.
Для амплитудного коэффициента пропускания ![]() воспользуемся
гауссовой аппроксимацией вида [6]:
воспользуемся
гауссовой аппроксимацией вида [6]:
где аL - эффективный радиус приемной апертуры;
![]() - спектральный
коэффициент пропускания приемной оптики.
- спектральный
коэффициент пропускания приемной оптики.
Подставляя (3)-(6) в (2), для пространственного спектра флуктуаций диэлектрической проницаемости воздуха вида:
![]() ,
,
с
учетом ![]() , в результате интегрирования будем иметь:
, в результате интегрирования будем иметь:
Здесь
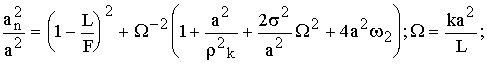

![]() ;
;
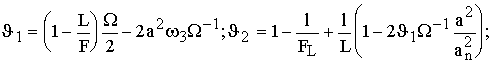

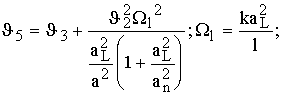
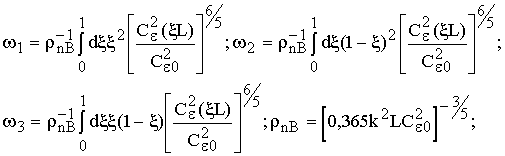
![]() (xL) -
структурная характеристика флуктуаций диэлектрической проницаемости воздуха
вдоль трассы распространения излучения;
(xL) -
структурная характеристика флуктуаций диэлектрической проницаемости воздуха
вдоль трассы распространения излучения; ![]() - структурная постоянная в окрестности
передатчика системы.
- структурная постоянная в окрестности
передатчика системы.
Функция ![]() определяется выражением [6]:
определяется выражением [6]:
В решаемой задаче при Т>>tk аналитически можно рассмотреть две ситуации:
1) полностью когерентное излучение:
![]()
2) флуктуации фазы комплексной амплитуды поля на выходе источника велики:
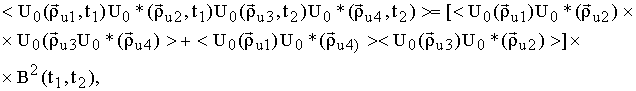 где
где
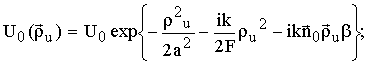
![]() - единичный
вектор перпендикулярный излучающей апертуре;
- единичный
вектор перпендикулярный излучающей апертуре;
b - случайный угол, под которым распространяется излучение.
Величина ![]() определяется по формуле (4), при этом в
ней делается замена переменных:
определяется по формуле (4), при этом в
ней делается замена переменных: ![]() .
.
Четвертый момент функции Грина G(.) по аналогии с [6] определяется выражением:
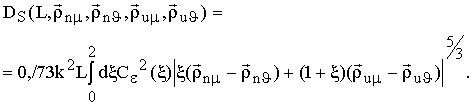
Конечные
выражения для ![]() громоздки и, поэтому, в статье не
приводятся.
громоздки и, поэтому, в статье не
приводятся.
С
использованием полученных соотношений проанализируем поведение ![]() , а также
моментов величины
, а также
моментов величины ![]() в зависимости от параметров передающего и
приемного каналов, интенсивности турбулентности атмосферы, а также отношения
в зависимости от параметров передающего и
приемного каналов, интенсивности турбулентности атмосферы, а также отношения ![]() . Упомянутые
зависимости получены для коллимированного излучения L/F=0 и
однородной трассы при
. Упомянутые
зависимости получены для коллимированного излучения L/F=0 и
однородной трассы при ![]() ;
;![]() =(10-13 -10-16 )м-2/3;
l=10-6 м; L=104м;
=(10-13 -10-16 )м-2/3;
l=10-6 м; L=104м;
![]() 0,1;
0,1; ![]() 0,1;
0,1;![]() =1;
=1; ![]() ,
, ![]() =10-5. Приведенные зависимости
показывают, что вероятность Рп (рис. 1) и величина
=10-5. Приведенные зависимости
показывают, что вероятность Рп (рис. 1) и величина ![]() (рис. 2) тем
больше, чем шире сам пучок (больше W) и лучше его
пространственная когерентность. Однако при этом
(рис. 2) тем
больше, чем шире сам пучок (больше W) и лучше его
пространственная когерентность. Однако при этом ![]() и Рп становятся более
чувствительным к точности нацеливания передающего канала на приемный,
поскольку с увеличением W или с уменьшением
и Рп становятся более
чувствительным к точности нацеливания передающего канала на приемный,
поскольку с увеличением W или с уменьшением ![]() происходит уменьшение пятна
подсвета приемной апертуры.
происходит уменьшение пятна
подсвета приемной апертуры.
Рис.1. Вероятность создания на приемнике излучения требуемого уровня лазерной энергии в зависимости от параметров и точности нацеливания пучка.
Одновременно
с этим в пятне возрастает плотность световой энергии и, как следствие,
величина ![]() становится
более чувствительной к отклонениям пучка от точки прицеливания.
становится
более чувствительной к отклонениям пучка от точки прицеливания.
Рис.2. Зависимость величины <Kn> от параметров и точности нацеливания пучка.
Любопытным
является тот факт, что при увеличении флуктуационной составляющей ошибки
нацеливания величина ![]() может быть максимизирована. Несмотря на
неожиданность данного результата, он объясняется очень просто. Увеличение
флуктуационной составляющей ошибки нацеливания эквивалентно расфокусировке
излучения передатчика в плоскости приемной апертуры. При этом очевидно, что при
больших смещениях пятна подсвета от точки прицеливания, энергия излучения на
последней может быть максимизирована за счет ее расфокусировки Расчеты показывают,
что она должна быть тем больше, чем шире пучок, выше степень его
пространственной когерентности, а также чем меньше интенсивность турбулентности
атмосферы. Другими словами турбулентность атмосферы, вызывая уширение пучка,
несколько «стирает» влияние ошибок нацеливания на
может быть максимизирована. Несмотря на
неожиданность данного результата, он объясняется очень просто. Увеличение
флуктуационной составляющей ошибки нацеливания эквивалентно расфокусировке
излучения передатчика в плоскости приемной апертуры. При этом очевидно, что при
больших смещениях пятна подсвета от точки прицеливания, энергия излучения на
последней может быть максимизирована за счет ее расфокусировки Расчеты показывают,
что она должна быть тем больше, чем шире пучок, выше степень его
пространственной когерентности, а также чем меньше интенсивность турбулентности
атмосферы. Другими словами турбулентность атмосферы, вызывая уширение пучка,
несколько «стирает» влияние ошибок нацеливания на ![]() и Рп. В целом,
влияние атмосферной турбулентности на среднее эффективность транспортировки
лазерной энергии тем заметнее, чем выше когерентность излучения, меньше длина
его волны и меньше радиус приемной апертуры, что совпадает с известными
результатами работ по исследованию похождения лазерного излучения в атмосфере
[6]. Наряду с отмеченным, установлено, что при переходе от коллимированного
излучения к сфокусированному L/F®1 ужесточаются требования к точности нацеливания. Нетрудно
показать, что для получения выигрыша в
и Рп. В целом,
влияние атмосферной турбулентности на среднее эффективность транспортировки
лазерной энергии тем заметнее, чем выше когерентность излучения, меньше длина
его волны и меньше радиус приемной апертуры, что совпадает с известными
результатами работ по исследованию похождения лазерного излучения в атмосфере
[6]. Наряду с отмеченным, установлено, что при переходе от коллимированного
излучения к сфокусированному L/F®1 ужесточаются требования к точности нацеливания. Нетрудно
показать, что для получения выигрыша в ![]() при фокусировке излучения в N раз
необходимо выполнение условия:
при фокусировке излучения в N раз
необходимо выполнение условия:
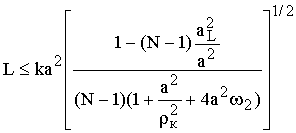 .
.
В противном случае предпочтительным является использование коллимированного излучения, поскольку фокусировка очень трудоемка.
Рис.3.
Зависимость величины ![]() от параметров и точности нацеливания
пучка.
от параметров и точности нацеливания
пучка.
На
рис. 3 представлены результаты исследований величины ![]()
![]()
![]() в зависимости от
вышеуказанных параметров. Результаты показывают, что величина
в зависимости от
вышеуказанных параметров. Результаты показывают, что величина ![]() увеличивается
с ростом пространственной когерентности излучения. Это связано с уменьшением
степени усреднения флуктуаций интенсивности пучка в плоскости приема
[6]. С
ростом s/а величина
увеличивается
с ростом пространственной когерентности излучения. Это связано с уменьшением
степени усреднения флуктуаций интенсивности пучка в плоскости приема
[6]. С
ростом s/а величина ![]() также увеличивается и тем значительнее,
чем больше смещение приемной апертуры от центра пятна подсвета к его периферии,
что обусловлено ростом дисперсии флуктуаций интенсивности пучка [6]. При
больших смещениях оси пучка от точки прицеливания наблюдается минимизация
относительной дисперсии величины
также увеличивается и тем значительнее,
чем больше смещение приемной апертуры от центра пятна подсвета к его периферии,
что обусловлено ростом дисперсии флуктуаций интенсивности пучка [6]. При
больших смещениях оси пучка от точки прицеливания наблюдается минимизация
относительной дисперсии величины ![]() в зависимости от флуктуационной
составляющей ошибки нацеливания. Этот результат с одной стороны объясняется
поведением среднего значения
в зависимости от флуктуационной
составляющей ошибки нацеливания. Этот результат с одной стороны объясняется
поведением среднего значения ![]() в зависимости от точности нацеливания
пучка (рис.1), а с другой - увеличением степени усреднения флуктуаций
интенсивности приемной апертурой. Наряду с этим, расчеты показали, что имеет
место увеличение относительной дисперсии
в зависимости от точности нацеливания
пучка (рис.1), а с другой - увеличением степени усреднения флуктуаций
интенсивности приемной апертурой. Наряду с этим, расчеты показали, что имеет
место увеличение относительной дисперсии ![]() при переходе от коллимированного излучения
к сфокусированному, а также при уменьшении длины волны излучения. Это
объясняется поведением параметров
при переходе от коллимированного излучения
к сфокусированному, а также при уменьшении длины волны излучения. Это
объясняется поведением параметров ![]() и
и ![]() и совпадает с известными результатами по
исследованию прохождения лазерного излучения в турбулентной атмосфере
[6].
и совпадает с известными результатами по
исследованию прохождения лазерного излучения в турбулентной атмосфере
[6].
Проведенный
анализ поведения вероятности ![]() и моментов величины
и моментов величины ![]() в зависимости от
параметров передающего канала, точности нацеливания и характеристик трассы
распространения излучения позволяет сформулировать следующий алгоритм
обоснования основных параметров системы транспортировки лазерной энергии (рис.
4).
в зависимости от
параметров передающего канала, точности нацеливания и характеристик трассы
распространения излучения позволяет сформулировать следующий алгоритм
обоснования основных параметров системы транспортировки лазерной энергии (рис.
4).
Исходя
из заданных характеристик приемника (![]() и ожидаемых условий распространения излучения (
и ожидаемых условий распространения излучения (![]() , L)
определяются дифракционные параметры передатчика системы (a, F,
, L)
определяются дифракционные параметры передатчика системы (a, F, ![]() ,l), максимизирующие величину <
,l), максимизирующие величину <![]() > при допустимой
точности нацеливания. Затем с использованием заданных параметров
> при допустимой
точности нацеливания. Затем с использованием заданных параметров ![]() ,
,![]() и полученных
параметров пучка (a, F,
и полученных
параметров пучка (a, F, ![]() ,l), определяется величина
,l), определяется величина ![]() , обеспечивающая
требуемую вероятность
, обеспечивающая
требуемую вероятность ![]() .
.
Рис.4. Алгоритм обоснования основных параметров системы транспортировки лазерной энергии.
Литература.
1. Системное проектирование радиосвязи: методы и обеспечение. - Воронеж: ВНИИС, 1994. - 287 с.
2. Дружинин В.В., Конторов Д.С. Системотехника. - М.: Радио и связь, 1985. - 200 с.
3. Левин Б.Р. Основы статистической радиотехники. - М.: Советское радио, 1989 - 659 с.
4. Глушков А.Н., Крекотень Б.П. Энергетический показатель качества лазерной системы связи // Тез. Докладов НТК "Направления развития лазерных и миллиметровых систем и средств в технике передачи информации и медицине. - Воронеж. - 1995. - С.21.
5. Глушков А.Н., Смагина Т.Ю. Статистические характеристики энергетического показателя качества лазерной системы связи // Сб. Докладов Всероссийской НТК "Радио и волоконно-оптическая связь, локация и навигация. - Воронеж. - 1997. - С. 1111-1120.
6. Зуев В.Е., Банах В.А., Покасов В.В. Оптика турбулентной атмосферы. - Л.: Гидрометеоиздат, 1988. - 270 с.
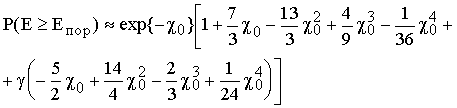
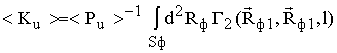 , (2)
, (2) (3)
(3)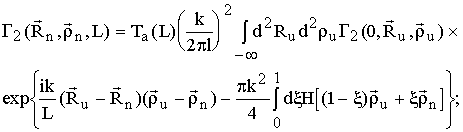 (4)
(4)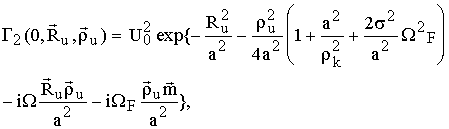 (5)
(5)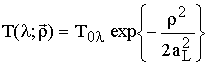 ,
(6)
,
(6)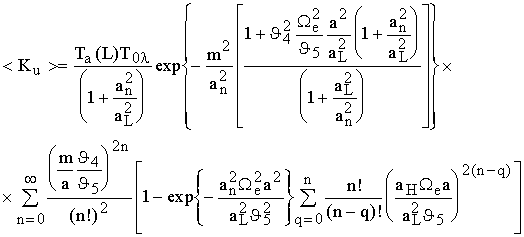
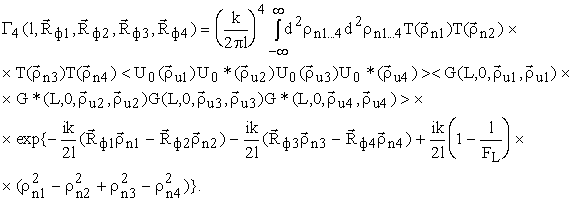 (8)
(8)