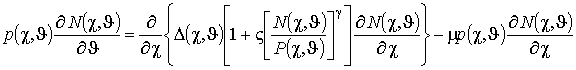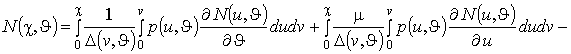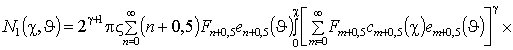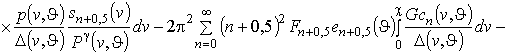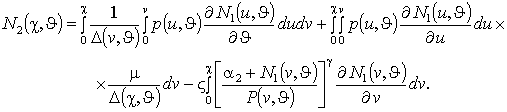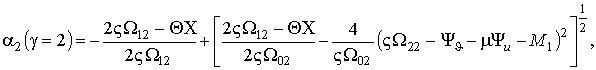"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ"  N 1, 2007

оглавление

дискуссия

УДК 539.219.3:669

АСИММЕТРИЗАЦИЯ ФОРМЫ РАСПРЕДЕЛЕНИЯ ПРИМЕСИ В ДЕЛЬТА-ЛЕГИРОВАННОЙ ОБЛАСТИ В ПРОЦЕССЕ ЕЕ ЗАРАЩИВАНИЯ

Е.Л. Панкратов
Институт физики микроструктур РАН, Нижний Новгород

Получена 4 января 2007 г.
 

С помощью предложенного в настоящей работе "макроподхода" проведен анализ динамики примеси в дельта - легированной области многослойной структуры в процессе ее заращивания покровным слоем. Проиллюстрированы причины систематически регистрируемой экспериментально асимметризации, не выявленные ранее при анализе перераспределения примеси в дельта-легированной области с помощью обычно используемого в литературе "микроподхода". На примере конкретных материалов многослойной структуры, дельта- и покровного слоев получена оценка уширения дельта-слоя.
 

Введение

Дельта-легирование твердотельных структур широко используется для совершенствования приборов микро- и оптоэлектроники и в настоящее интенсивно развивается [1-3]. Такой способ легирования используется, например, для улучшения параметров диодов Шоттки [4,5], гетеробиполярных транзисторов [5] и т.д.

Дельта-слой представляет собой тонкий слой, сформированный в процессе эпитаксиального роста многослойной структуры (МС) как один из ее внутренних слоев. В процессе роста МС происходит уширение и асимметризация дельта-слоев [1,2], что может привести к отклонениям характеристик содержащих дельта-слои приборов от запланированных значений. В литературных источниках эти эффекты объясняются диффузией, рассмотренной в наиболее простейшем предельном случае (при постоянном коэффициенте диффузии и -образном начальном распределении, эволюционирующем с течением времени в бесконечной среде), и сегрегацией. При этом для анализа перераспределения примеси использовался "микроподход" (см., например, [6] и аналогичные работы), использование которого при большом количестве примеси может привести к большим объемам вычислений. Известно, что динамика перераспределения примеси в процессе роста МС зависит от ее свойств (например, от коэффициентов диффузии примеси в слоях МС), а также – от параметров самого процесса эпитаксии (например, от скорости и температуры роста). Эти характеристики могут быть использованы при анализе перераспределения примеси в процессе ее заращивания в рамках "макроподхода", позволяющего при большом количестве примеси существенно уменьшить объем вычислений.

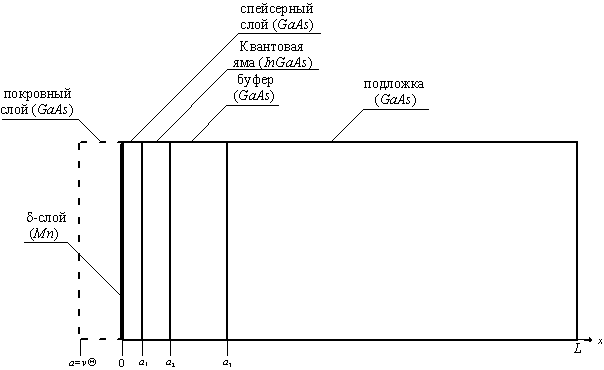
Основной целью данной работы является анализ влияния свойств материалов слоев МС и параметров процесса эпитаксии на динамику перераспределения примеси в дельта-легированной области в процессе роста МС. Сопутствующей целью данной работы является поиск методики анализа перераспределения примеси в рамках континуального аппарата. Такой анализ проводился на примере МС, приведенной на рис.1. Второй целью данной работы является количественная оценка уширения дельта-слоя в процессе роста покровного слоя (ПС).
 

Методика и результаты анализа

Динамика примеси в дельта-легированной области рассматриваемой МС может быть описана с помощью второго закона Фика [1,7-9]

,             (1)

где – пространственно-временное распределение концентрации при-меси,  – пространственно-временное распределение потока примеси,  и  – соответственно коэффициент диффузии примеси в МС и пористость слоев МС [7-9]. Пространственная зависимость коэффициентов  и  уравнения (1) определяется изменением свойств МС от
 

Рис. 1. МС GaAs/InGaAs/GaAs/GaAs с d-слоем марганца и ПС GaAs полной толщины .  - момент окончания роста ПС

 

слоя к слою. Различными могут быть плотность слоев, слои могут содержать примеси (например, индий из-за процесса взаимодиффузии слоев) и другие дефекты слоев. Концентрационная зависимость коэффициента диффузии, которая может быть аппроксимирована полиномом следующего вида  [7], вносит заметный вклад в коэффициент диффузии в случае большого количества примеси. Обычно  принимает целые значения в интервале  (см., например, [7]),  – предел растворимости примеси в МС. Для определения пространственно-временного распределения концентрации  уравнение (1) необходимо дополнить граничными и начальным условиями. Начальное распределение  принималось гауссовым с полушириной, равной полуширине полного количества монослоев примеси. Граничное условие в окрестности начала координат в общем случае имеет вид: , где  – скорость роста покровного слоя (ПС) GaAs. Обычно полная длительность Q и температура роста T имеют такие значения, при которых примесь не достигает границы МС . По этой причине на границе МС  можно считать .

Для анализа динамики примеси в различных режимах роста ПС найдем решение уравнения (1). Представляет интерес переход от переменных  и  и коэффициента диффузии  к безразмерным переменным  и  и безразмерному коэффициенту диффузии , введенных с помощью следующей замены ,  и , где  – среднее значение коэффициента диффузии. После такой замены уравнение диффузии принимает вид

,           (2)

где . Граничные и начальное условия в новых переменных запи-сываются в следующей форме: , , , где , . В окрестности границы  (т.е. ) рассматриваемой МС (рис.1) слагаемым  можно пренебречь по сравнению со слагаемым . Такое приближение позволяет записать последнее граничное условие в упрощенном виде:  и анализировать динамику примеси в смещающейся области длины . Для оценки пространственно-временного распределения примеси представляют первоочередной интерес аналитические методы из-за их большей наглядности по сравнению с численными методами. Аналитическую оценку функции  проведем путем решения эквивалентного дифференциальному уравнения (2) интегро-дифференциального уравнения следующего вида

                   .                                                                  (3)

Решение данного уравнения будем искать методом осреднения функциональных поправок. В первом приближении по методу осреднения функция  и ее производные заменяются их постоянными составляющими в правой части уравнения (3) [10]: ,  и . Далее полученное решение уточняется. Однако, замена функции  на более точную аппроксимацию в правой части (3) вместо среднего значения позволяет ускорить сходимость алгоритма оценки решения уравнения (3). В качестве более точной аппроксимации воспользуемся решением уравнения диффузии в простейшем случае постоянного коэффициента диффузии и фиксированных во времени границ МС. Может быть показано (см., например, [11]), что постоянная составляющая коэффициента диффузии  часто является наиболее удачной при выборе аппроксимации изменений коэффициента диффузии постоянной величиной. Решение уравнения диффузии при постоянном коэффициенте диффузии может быть получено стандартными методами (см., например, [9,11,12]) и записано в следующем виде

,                              (4)

где ,,.Подстановка (4) в (3) позволяет получить первое приближение концентрации примеси по методу осреднения функциональных поправок с ускоренной сходимостью

                   ,                             (5)

где ,.Второе приближение функции  может быть получено стандартной (см., например, [10]) заменой в правой части уравнения (2), т.е. . Такая замена приводит к следующему результату

                (6)

Параметр a₂ определяется соотношением [10]

                                    ,                                                     (7)

где . Подстановка (5) и (6) в (7) позволяет получить

,

,

,,

, .

Второе приближение концентрации примеси позволяет получить основные физические выводы из анализа перераспределения примеси в различных режимах роста МС и сделать приближенные оценки концентрации и уширения дельта-слоя. При необходимости могут быть получены приближения третьего, четвертого и т.д. порядка по аналогии с приближением второго порядка. С целью уточнения полученных результатов использовались также и численные методы, но они обладают меньшей наглядностью, чем аналитические.

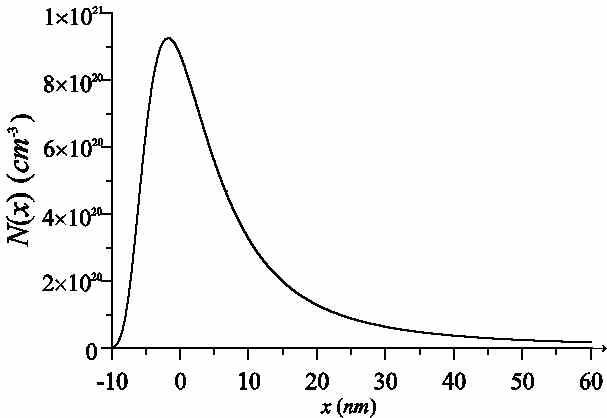
Далее проведем анализ динамики перераспределения примеси при различных режимах заращивания дельта-легированной области. В первом режиме роста ПС между окончанием роста дельта-слоя и началом роста ПС существует перерыв технологического процесса. Такая пауза приводит к диффузии примеси в спейсерный слой еще до начала роста ПС и, как следствие, к начальной асимметрии дельта-слоя (см. рис.2). Диффузионный процесс, протекающий до начала роста ПС, может быть учтен выбором асимметричного начального условия для диффузионного процесса, протекающего во время заращивания. Асимметрия свидетельствует об искажении дельта-слоя, что приводит к изменению свойств легированной структуры и, как следствие, к необходимости уменьшения длительности прерывания технологического процесса.

По этой причине на следующем этапе анализа динамики примеси рассмотрим предельный случай пренебрежимо малых прерываний роста МС. В таком предельном случае возможна реализация двух режимов. В первом из них (режиме медленного роста ПС или малых длительностях быстрого роста ПС) на границе МС  () всегда присутствует примесь.
 

Рис. 2. Распределение примеси с учетом паузы между окончанием формирования d-слоя и началом формирования ПС

 

Длительность  роста ПС,  соответствующую  такому  процессу, можно оце-нить с помощью соотношения:  (т.е. толщина ПС меньше эффективной диффузионной длины примеси). Распределение примеси при таком режиме роста приведено на рис. 3а и 3б для случаев, когда динамические свойства ПС и спейсерного слоя соответственно идентичны и различны. В качестве примеси и слоев МС рассматривались материалы, указанные на рис.1. Использованная для расчета данных и последующих распределений температурная зависимость коэффициента диффузии марганца в арсениде галлия  приведена в [13]. Предел растворимости марганца в арсениде галлия, принятый равным  см^-3, приведен в ссылках [14]. Длительность, скорость и температура роста выбирались таким образом, чтобы примесь не достигала содержащего индий слой.

 

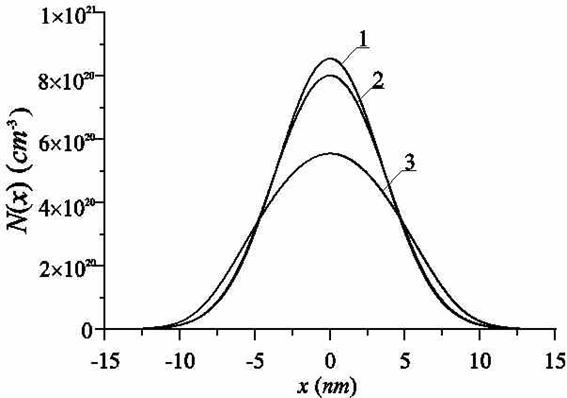
Рис. 3а. Распределение марганца при малых скоростях и малых временах роста ПС в приближении идентичности свойств ПС и спейсерного слоя при температурах роста 300°С, 450°С и 550°С (соответственно кривые 1-3)
 

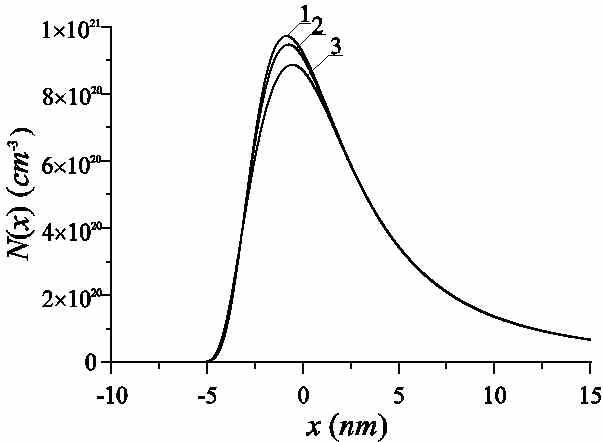
Рис. 3б. Расчетное распределение марганца при малых скоростях и малых временах роста ПС при различных свойствах ПС и спейсерного слоя при температурах роста 300°С, 450°С и 550°С (соответственно кривые 1-3)

Во втором  режиме  роста ПС (режим  быстрого  роста ПС при  большихдлительностях заращивания) на границе МС x=-vt () и в ее окрестности примесь отсутствует. Длительность роста ПС, соответствующая такому режиму роста, может быть оценена с помощью соотношения:  (т.е. толщина ПС больше эффективной диффузионной длины примеси). Рассматриваемый режим роста представлен на рис.4а и 4б для случаев, когда свойства ПС и спейсерного слоя соответственно одинаковы и различны. Сравнение рисунков 3а и 3б, а также рис. 4а и 4б друг с другом показывает, что различие свойств ПС и спейсерного слоя также приводит к асимметрии дельта-слоя. Анализ динамики перераспределения примеси показал, что выбором режима заращивания распределения примеси в дельта-слое можно сделать более симметричным. Для симметризации должно выполняться  условие:    (параметры с индексом 1 соответствуют ПС, параметру с индексом 2 соответствуют спейсерному слою).
 

Рис. 4а. Расчетное распределение марганца при больших скоростях (больших временах) роста ПС в приближении идентичности свойств ПС и спейсерного слоя при температурах роста 300°С, 450°С и 500°С (кривые соответственно 1-3)
 

Рис.4б. Расчетное  распределение марганца при больших скоростях и больших временах роста ПС при различных свойствах ПС и спейсерного слоя при температурах роста 300°С, 450°С и 550°С (кривые соответственно 1-3)

 

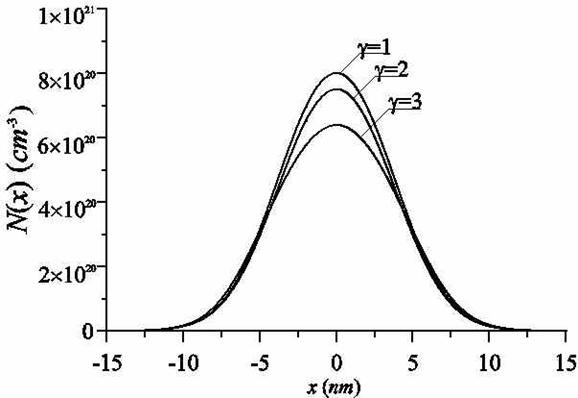
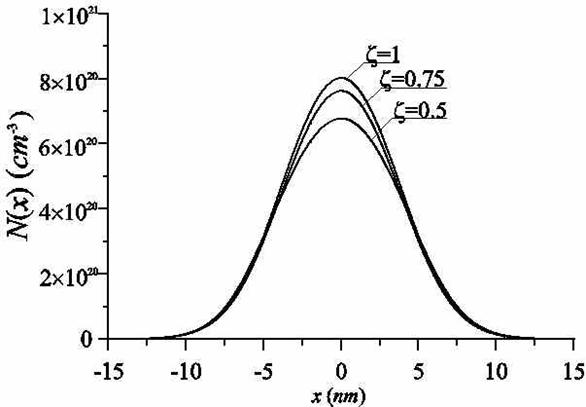
Зависимость формы распределения примеси от вида нелинейности материалов МС, т.е. от величины параметров  и  проиллюстрирована соответственно на рис.5 и 6. Данные рисунки показывают, что увеличение параметров  и  приводит к уширению дельта-слоя, а не к его асимметризации.

На рис.7 приведено сравнение расчетных распределений концентрации марганца в арсениде галлия, полученных в настоящей работе, с аналогичными экспериментальными распределениями, приведенными в [2] для нескольких значений температуры.

 

Рис. 5. Расчетные распределения марганца при различных значениях g для температуры роста 450°С
 

Рис. 6. Расчетные  распределения марганца при различных значениях z для температуры роста 450°С
 

Рис. 7. Расчетные (соответственно кривые 1-3) и полученные в [2] экспериментальные (соответственно кривые 4-6) распределения марганца при температурах роста 220°С, 300°С и 400°С (кривые соответственно 1 и 4, 2 и 5, 3 и 6)

 

На основе  полученного  решения  уравнения  диффузии проведем коли-чественную оценку относительного уширения дельта-слоя , где d – реальное уширение дельта-слоя,  - полуширина начального распределения примеси на уровне 0,5 от максимального значения концентрации. В качестве критерия оценки изменения ширины дельта-слоя выберем ее изменение на уровне 0,5 от максимального значения концентрации марганца. Попадание примеси в квантовую яму нежелательно. По этой причине в первую очередь представляет интерес уширение дельта-слоя вправо. Альтернативным критерием оценки уширения дельта-слоя является равновеликий по площади прямоугольник подробно рассмотренный в [15,16]. Применение обоих критериев приводит к близким по величине результатам. Результаты оценки приведены на рис. 8 и 9 в зависимости от температуры роста и полной толщины ПС . Последние рисунки показывают монотонный рост относительного уширения дельта-слоя от температуры и полной толщины ПС.
 

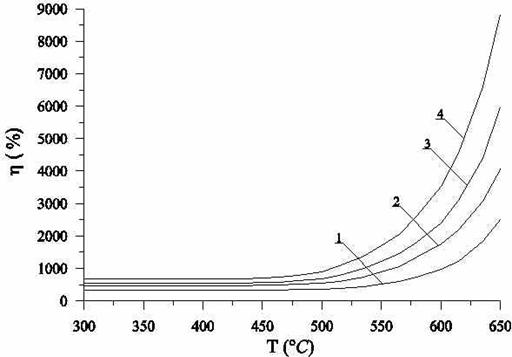
Рис. 8. Зависимость относительного уширения L дельта-слоя от температуры роста ПС при толщинах покровного слоя в 50 нм, 100 нм, 150 нм и 200 нм (соответственно кривые 1-4)

 

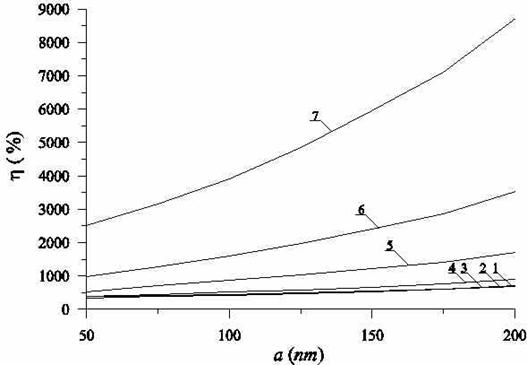
Рис. 9. Зависимость относительного уширения L дельта-слоя от максимальной толщины ПС при температурах роста 300°С, 400°С, 450°С и 500°С (кривые соответственно 1-4)

Заключение

В настоящей работе проведен анализ зависимости динамики перераспределения примеси, поступающей в многослойную структуру из дельта-слоя, в процессе его заращивания покровным слоем от характеристик многослойной структуры и эпитаксиального роста. При определении причин выявленной ранее экспериментально асимметризации дельта-слоя в процессе его заращивания показано, что искажение формы распределения примеси может быть объяснено не только с помощью комбинации двух процессов, т.е. рассмотренной в наиболее простейшем предельном случае диффузии и сегрегации (т.е. при рассмотрении дискретной модели массопереноса в рамках "микроподхода"), а с помощью одного процесса, т.е. диффузии при более точном ее учете (т.е. с учетом пространственной зависимости коэффициента диффузии и других характеристик МС). В результате проведенного анализа получены условия, позволяющие уменьшить асимметризацию. На примере дельта-слоя марганца, сформированного на многослойной структуре GaAs/InGaAs/GaAs/ GaAs и покровного слоя GaAs получена оценка уширения дельта-слоя и проанализирована в зависимости от температуры и длительности роста покровного слоя.

 

Данная работа поддержана Госконтрактом (№02.442.11.7342) и грантом РФФИ (№ 05-02-17340-a)

 

Литература
 

[1] Schubert E.F. // J. Vac. Sci. Technol. A. 1990. V. 8. № 3. P. 2980.

[2] Nazmul A.M., Sugahara S., Tanaka M. // Journal of the crystal growth. 2003. V.251. P. 303.

[3] Li G., Jagadish C. // Solid-State Electronics. 1997. V. 41, №9. P. 1207.

[4] Шашкин В.И., Мурель А.В., Данильцев В.М., Хрыкин О.И. // ФТП. 2002. T. 36. №5. С. 537.

[5] Васильев В.К., Васильева Ю.В., Данилов Ю.А., Звонков Б.Н.// Поверхность. Рентгеновские, синхротронные и нейтронные исследования. 2004. №4. С32.

[6] Ni W.-X., Hansson G.V., Sundgren J.-E. et al. // Phys. Rev. B. 1992. V. 46. P. 7551.

[7] Готра З.Ю. Справочник. Технология микроэлектронных устройств. М.: Радио и связь, 1991.

[8] Grebene A.B. Bipolar and MOS analogous integrated circuit design. New York: John Wyley and Sons, 1983.

[9] Тихонов А.Н., Самарский А.А. Уравнения математической физики. М.: Наука, 1972.

[10] Соколов Ю.Д. // Прикладная механика. 1955. Т. 1. С. 23.

[11] Панкратов Е.Л. // Изв. вузов ПНД. 2004. T. 12. №3. C. 35.

[12] Pankratov E.L. // Phys. Rev. B. 2005. V. 72. №7. P. 075201.

[13] Хлудков С.С., Корецкая О.Б. // Известия вузов. Физика. 1985. Т. 28. № 1. С. 107.

[14] Данилов Ю.А., Круглов А.В., Питиримова Е.А. и др. // Изв. РАН. Серия физическая. 2004. Т. 68. №1. С. 65.

[15] Малахов А.Н., Панкратов Е.Л. // Известия вузов. Радиофизика. 2001. Т. 44. №4. С. 367.

[16] Coffey W.T., Crothers D.F.S., Kalmykov Yu.P. // Physical Review E 1997. V. 55. N 4. P. 4812