Диапазонные свойства зонированного рефлектора

 

А. И. Амосова 

Институт радиофизики и электроники им. А. Я. Усикова
Национальной академии наук Украины, г. Харьков

 

Получена 15 января 2008 г. 

 

       Методами FDTD с точными "поглощающими" условиями на виртуальных границах исследованы электродинамические характеристики зонированного параболоцилиндрического рефлектора. Установлено, что отличия основных антенных характеристик зонированного зеркала по сравнению с характеристиками сплошного зеркала с такой же апертурой могут быть минимизированы до заданного уровня при существенном улучшении массогабаритных параметров антенной системы. Получены ранее неизвестные данные о распределении полей вблизи границ секций рефлектора, в том числе – в области "тени".

 

Благодаря простоте конструкции и хорошим электродинамическим характеристикам зеркальные антенны широко применяются в тех диапазонах длин волн, где при относительно небольших геометрических размерах всей конструкции достаточно просто достигаются весьма значительные электрические размеры апертур, которыми, в основном, и определяются электродинамические характеристики антенны [1, 2].

         В тоже время, зеркальным антеннам присущ недостаток принципиального характера, который обусловлен применением зеркал с отражающими поверхностями второго порядка. Он состоит в, так называемом, "эффекте опережающего роста массы" (масса зеркала растет быстрее, чем его апертура) и особенно ярко проявляется при создании антенн с предельно достижимыми электродинамическими характеристиками и, следовательно, геометрически большими апертурами [3, 4].

 В связи с этим поиск новых решений в конструировании зеркальных антенн и в настоящее время представляется актуальной задачей. Более того, на самом деле, он и не прекращался на протяжении всей истории развития зеркальных антенн (см., например, [5–11]).

         Один из путей ослабления "эффекта опережающего роста массы" состоит в конструировании рефлектора из отдельных секций – зонировании рефлектора. Это позволяет улучшить массогабаритные параметры антенны и уменьшить ветровую нагрузку на зеркало. С другой стороны, рост количества электродинамически значимых элементов антенны, как правило, сопровождается ухудшением ее диапазонных свойств. Так, например, коэффициент использования поверхности (КИП) у антенн Кассегрена часто достигает значения , в то время как у однозеркальных антенн обычно не превышает  [2]. Однако при этом полоса рабочих частот антенны сужается, так как уже определяется не только размерами облучателя и антенного зеркала, но и размерами контррефлектора. В еще большей степени это присуще многозеркальным антеннам.

Относительно небольшое количество данных о влиянии разбиения рефлектора на отельные секции объясняется, с одной стороны, экспериментальными трудностями, особенно при исследованиях в ближней зоне, а с другой – отсутствием достаточно универсального и мощного метода теоретического исследования таких структур, который бы обеспечивал получение достоверных результатов. В связи с этим представляется актуальным исследование диапазонных свойств антенного рефлектора, состоящего из отдельных секций, FDTD-методом с точными «поглощающими» условиями на виртуальных границах пространства счета.

         Рассмотрим рефлектор, который образован трансляцией вдоль оси  декартовой системы координат дуг конфокальных парабол  (,  – фокусные расстояния, ), ограниченных слоем . При этом ,  и все  (рис. 1). Предположим, что самая длинная рабочая волна мала в сравнении с размерами структуры вдоль , т. е. – . В качестве облучателя выберем оптимальный -секториальный рупор, линия фазовых центров которого совпадает с фокальной осью, а плоскость апертуры ортогональна плоскости симметрии рефлектора, который возбуждается "нитью" электрического тока.  

 

 

  

 

Рис. 1. Зонированный параболический рефлектор. , , ,  (штриховыми линиями в области  показано продолжение сплошного рефлектора).

 

В настоящей работе реализация программы исследований зонированных структур в математическом и вычислительном планах осуществлена путем эквивалентной замены оригинальных открытых начально-краевых задач соответствующими модифицированными закрытыми задачами и базируется на результатах работ [12, 13] для случая плоских двумерных модельных задач теории излучателей несинусоидальных волн. Их решения сводятся к отысканию решений ,  двумерного телеграфного уравнения

 

,

 

удовлетворяющего условиям Дирихле на  достаточно гладкой границе  металла ;  и начальным условиям

 

.

 

Здесь  – замыкание области анализа .

         В предположении, об ограниченности носителей функций , , , ,  и занятой "металлом" области пространства при всех  в , решение задачи существует и единственно для любого значения  и принадлежит пространству Соболева.

Неограниченная область анализа  редуцируется до конечной области  с помощью точных локальных "поглощающих" условий, построенных в работе [13], которые являются прямым следствием классических условий излучения и, таким образом, придают недостающие атрибуты строгости постановке открытой начально-краевой задачи.

На рис. 2 представлены результаты численного анализа диаграмм направленности зонированного () и сплошного рефлекторов для длин волн  (синфазное возбуждение) и . При этом размеры апертуры и фокусное расстояние  сплошного рефлектора такие же, как у третьей (наибольшей) секции, т.е. – . Сплошные линии соответствуют данным, полученным апертурным методом, пунктирные – данным, полученным в рамках подхода, разрабатываемого в настоящей работе. В случае сплошного рефлектора (рис. 2,а) в пределах главного лепестка ДН оба метода дают практически одинаковые результаты. Однако, уже в области первых и, тем более дальних, боковых лепестков имеются различия, обусловленные недостатками приближенного метода: неточным заданием амплитудно-фазового распределения поля в апертуре; пренебрежением краевыми эффектами и полем на "теневой" стороне зеркала. В случае зонированного рефлектора эти недостатки апертурного метода проявляются еще сильнее (рис. 2,б). Так, например, из результатов строгого анализа следует, что девиация  приводит к возникновению максимальной квадратичной фазовой ошибки на краю апертуры , что отражается в наличии «провала» по центру главного лепестка и "заплывании" минимумов ДН. Эти эффекты, практически, не отражаются на результатах счета с использованием апертурного метода, но легко обнаруживаются при строгом анализе.

 

 

Рис. 2. Нормированные диаграммы направленности целого зеркала (а), зонированного зеркала (б) (сплошная линия – апертурный метод, пунктирная – FDTD).

 

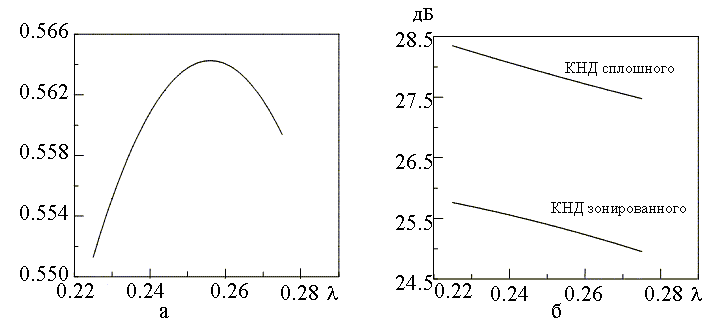
Более подробно изменения электродинамических характеристик, к которым приводит разделение рефлектора на секции, иллюстрируется рисунком 3, на котором в интервале длин волн  представлены отношение КИП зонированного рефлектора к КИП сплошного рефлектора (а) и коэффициенты направленного действия (КНД) зонированного и сплошного рефлекторов (б).

                         Рис. 3. Отношение КИП зонированного зеркала к КИП сплошного зеркала (а), коэффициенты направленного действия (б).

 

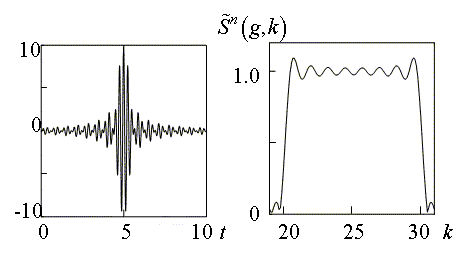
Рис. 4. Временная реализация и спектр сигнала источника в свободном пространстве

 

 

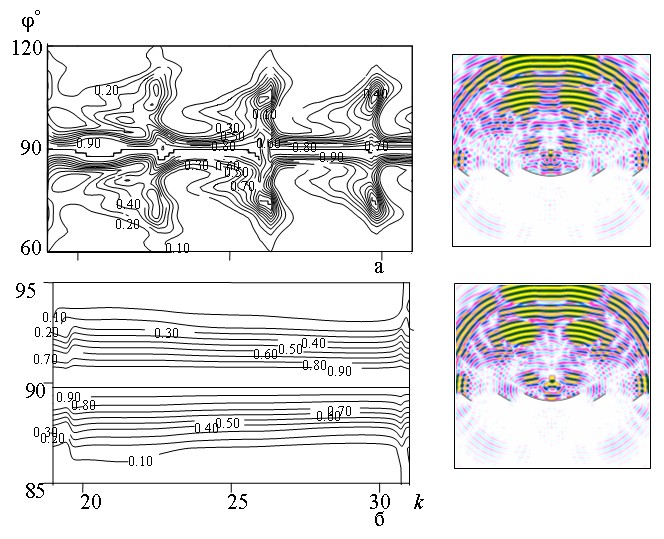
Наиболее наглядно и полно диапазонные свойства рассматриваемой структуры при возбуждении импульсным полосовым сигналом, временная реализация и спектр которого показаны на рис. 4, иллюстрируются широкополосной диаграммой излучения. На рис. 5 в координатах  (здесь  – волновое число;  – угол в плоскости ) представлена диаграмма излучения зонированного рефлектора, любое сечение которой плоскостью  представляет собой обычную диаграмму направленности исследуемой антенны в -плоскости. Периодическое расширение интервалов значений угловой координаты , соответствующей одному и тому же уровню поля, с изменением

Рис. 5. Диаграммы излучения в полосе частот (а – , б –)

 

 

волнового числа  обусловлено ростом квадратичных фазовых ошибок в пределах  (=1,2,… – целое). Из сравнения результатов численного эксперимента, выполненного при различных апертурах облучателя, видно, что при увеличении апертуры облучателя (от  до ;  – длина волны, соответствующая центральному значению частоты, при которой апертура рефлектора возбуждается синфазно) снижение уровня облучения краев рефлектора, как и следовало ожидать, приводит уменьшению влияния квадратичных фазовых ошибок на излучаемые антенной поля. При этом результаты вычислительного эксперимента свидетельствуют о возможности такого выбора параметров структуры, который бы обеспечивал заданную полосу рабочих частот антенны.

          Отметим еще одно важное свойство исследуемой структуры, а именно: – из результатов численных экспериментов следует, что при возбуждении зонированного рефлектора -поляризованным полем неоднородной цилиндрической волны, исходящей из фокальной оси рефлектора, ниже плоскости  поле, практически, отсутствует. Во всяком случае, его значение не превышает дБ от максимума в направлении , что весьма важно при практическом проектировании антенн с секционированными рефлекторами.

          Таким образом, основываясь на приведенных выше результатах численных исследований, можно утверждать, что оптимальный выбор параметров облучателя и зонированного рефлектора позволяет обеспечить заданную рабочую полосу частот исследуемой антенны при допустимом снижении коэффициента усиления. Применение зонированных рефлекторов открывает широкие перспективы оптимизации массо-габаритных параметров антенных систем и, таким образом, позволяет существенно снизить отрицательное влияние "эффекта опережающего роста массы" на технико-экономические показатели зеркальных антенн.

 

Литература

 

1. Кюн Р. Микроволновые антенны: Пер. с нем. – Л.: Изд-во «Судостроение», 1967. – 518 с.

2. Вуд П. Анализ и проектирование зеркальных антенн: Пер. с англ. – М.: Радио и связь, 1984. – 208 с.

3. Советские радиотелескопы и радиоастрономия Солнца / Гельфрейх Г. Б., Зайцев В. В., Илясов Ю. П. и др. – М.: Наука, 1990. – 212 с.

4. Хансен Р. К. Сканирующие антенные системы СВЧ: Пер. с англ. – М.: Сов. радио, 1966. – 536 с.

5. Provencher J. H. Experimental study of adiffraction reflector // Trans. IRE. – 1960. – Vol.8, №3. – P.331-336.

6. Ronchi L., Russo V., DiFrancia G. T. Stepped cylindricsl antennas for radio astronomy // Trans. IRE. – 1961. – Vol.9, №1. – P. 68-74.

7. Ronchi L., DiFrancia G. T. An application of parageometrical optics to the design of a microwave mirror // Trans. IRE. – 1958. – Vol.6, №1. – P.129-133.

8. Domakov A. I., Shugaev S. V. The directional properties of multiring zone antennas // Proc. International Conf. On Antenna Theory and Techniques. – Kyiv (Ukraine) – 2005. – P.173-175.

9. Rotman W. Wide-angel scanning with microwave double-layer pillboxes // Trans. IRE. – 1958. – Vol.6, №1. – P. 96-105.

10.  Courtney C. C., Baum C. E. Coaxial beam-rotation antenna (COBRA) concepts // Sensor and Simulation Note. – 1996. – №395. – 38 p.

11.  Atchley L. M., Farr E. G., Toy J. S., Merced N., Altgilbers L. L. Development and testing of a parachute deployable impulse radiating antenna // Sensor and Simulation Note. – 2002. – №465. – 30 p.

12. Сиренко Ю. К. Моделирование и анализ переходных процессов в открытых периодических, волноводных и компактных резонаторах. – Харьков: Эдена, 2003. – 363 с.

13. Сиренко Ю. К., Пазынин В. Л., Вязьмитинова А. И., Сиренко К. Ю. Компактные неоднородности свободного пространства: виртуальные границы в скалярных и векторных «открытых» начально-краевых задачах теории рассеяния несинусоидальных электромагнитных волн. – Электромагнитные волны и электронные системы, 2003, т. 8, №11-12, с. 33–54.