РОБАСТНОЕ СОВМЕСТОЕ ОБНАРУЖЕНИЕ И ОЦЕНКА ПАРАМЕТРОВ
РАДИОИМПУЛЬСОВ НА ФОНЕ СОВПАДАЮЩИХ ПО СПЕКТРУ ПОМЕХ
В.И.Неволин, В.В.Беленьков
Филиал ГОУ ВПО "Южно-Уральский государственный университет", г. Кыштым
Получена 27 декабря 2011 г.
Аннотация. Рассматриваются общетеоретические вопросы построения радиотехнических и радиолокационных систем, синтезируемых как в классе гладких совпадающих по спектру помех, так и общих разрывных марковских случайных процессов на основе функции влияния теории робастных статистик. Используется новый условно-параметрический подход в виде критерия оптимального робастного обнаружения и метода робастной нелинейной фильтрации. Синтезируемые алгоритмы реализуются в форме нелинейных дифференциальных уравнений со случайной правой частью, решаемых численными методами.
Ключевые слова: Робастное обнаружение, Метод функций влияния, Марковские процессы, Нелинейные дифференциальные уравнения, Критерий оптимального робастного обнаружения, Метод оптимальной нелинейной фильтрации.
Abstract. We consider theoretical questions of constructing radio and radar systems, synthesized in the class of smooth matching of spectrum interference, and general discontinuous Markov processes based on influence functions of the theory of robust statistics. Using a new quasi-parametric approach as a criterion for the optimal robust detection and method of robust nonlinear filtering. Synthesized algorithms are implemented in the form of nonlinear differential equations with random right-hand side that can be solved numerically.
Keywords: Robust detection, The
method of influence functions, Markov Processes, Nonlinear differential
equations, Optimal Robust detection, optimal nonlinear filtering.
Введение
В настоящее время в теории и практике создания сложных радиотехнических систем, прежде всего радиолокационных, начинают все более широко применяться для решения статистических задач методы, свободные от распределений [1],[2]. Следует отметить, что теоретические аспекты создания таких систем, функционирующих на принципах непараметрических статистик, находятся в состоянии интенсивных исследований. И наиболее действенные практические результаты, как правило, на основе полуэвристичеких методов, были получены при использования робастных приближений реальных непараметрических распределений статистик ограниченных объемов при решении нестационарных задач, в том числе и в радиолокационных системах, [1]-[3]. Широко используемым методом преодоления априорной неопределенности также является метод Роббинсона или эмпирический байесовский подход, когда оценки неизвестных априорных данных формируются на основе апостериорных. Причем для многих задач практической потребности, но далеко не для всех, метод Роббинсона является достаточно действенным с осязаемой смысловой значимостью.
В качестве нового подхода в данном направлении предлагается метод нелинейной
робастной фильтрации [2], основывающийся на условно-параметрическом методе
обнаружения нестационарных сигналов при действии произвольных помех. Этот
метод позволяет организовать функционирование радиолокационных и информационных
систем как в условиях статистической априорной неопределенности, так и в
условиях мощных помех. Т.е. тогда, когда даже при известных распределениях
помех, например, при аддитивном белом шуме, функции правдоподобия (функционалы
правдоподобия) становятся многомодальными, а именно, распределениями
неизвестного функционального вида. При этом методология математического синтеза
новых алгоритмов обработки базируется на принципах теории робастных
статистик и марковских случайных процессов, а алгоритмы реализуются в виде
систем нелинейных дифференциальных уравнений.
2. Общая концепция решения непараметрических информационных задач
В
большинстве реальных практических задач состояние информационных систем может
аппроксимироваться в общем случае многосвязными марковскими процессами,
например, в форме непрерывного марковского процесса ![]() . Однако во многих задачах можно
использовать односвязный марковский процесс, полностью представляемый
вероятностями переходов, например, в виде
. Однако во многих задачах можно
использовать односвязный марковский процесс, полностью представляемый
вероятностями переходов, например, в виде
![]() , (2.1)
, (2.1)
где ![]() - безусловная плотность
распределения вероятностей (ПРВ),
- безусловная плотность
распределения вероятностей (ПРВ), ![]() - вероятность переходов (условная ПРВ для
дискретных значений случайной величины из состояния
- вероятность переходов (условная ПРВ для
дискретных значений случайной величины из состояния ![]() в состояние
в состояние ![]() .
.
Если обозначить для цепей
Маркова, приняв дискретные состояния как ![]() ,
в общепринятых обозначениях вероятность переходов как
,
в общепринятых обозначениях вероятность переходов как ![]() ,
то из уравнения (2.1) можно получить следующее уравнение Маркова для
соответствующих вероятностей переходов в цепи Маркова с конечным числом
состояний
,
то из уравнения (2.1) можно получить следующее уравнение Маркова для
соответствующих вероятностей переходов в цепи Маркова с конечным числом
состояний
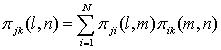 ,
где
,
где
![]()
![]() . (2.2)
. (2.2)
И это уравнение является частным случаем общего уравнения Колмогорова-Чепмена, в том числе для цепей Маркова, с бесконечным числом состояний.
Как известно, например, [2], [4], в общей форме для марковского процесса можно получить следующее уравнение для ПРВ
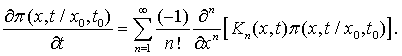 (2.3)
(2.3)
В уравнении (2.3)
коэффициенты
![]() определяются
как
определяются
как
 . (2.4)
. (2.4)
В более общей форме,
используя условия согласованности для многомерной плотности распределения
вероятностей как ![]() ,
,
уравнение для одномерной плотности распределения вероятностей непрерывного марковского процесса от уравнения (2.3) после соответствующих несложных преобразований, например, как в [2], приводится к виду
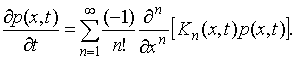 (2.5)
(2.5)
Если коэффициенты в (2.5),
т.е., ![]() при
при ![]() , то непрерывный марковский
процесс называется диффузионным, а уравнение (2.5) переходит в уравнение
Фоккера-Планка- Колмогорова (ФПК)
, то непрерывный марковский
процесс называется диффузионным, а уравнение (2.5) переходит в уравнение
Фоккера-Планка- Колмогорова (ФПК)
где ![]() - соответственно
являются коэффициентами сноса и диффузии и обозначаются также как локальные
характеристики диффузионного марковского процесса.
- соответственно
являются коэффициентами сноса и диффузии и обозначаются также как локальные
характеристики диффузионного марковского процесса.
Как отмечено в [1],[2],[5] широко распространенные в настоящее время реальные непараметрические задачи решаются, как правило, интуитивно, а значит с невысокой помехоустойчивостью. Решение соответствующих задач для информационных систем по разработанным в [2] подходу и методологиям основываются на использовании марковских процессов. Можно обоснованно считать, что методология марковских процессов является в настоящее время наиболее мощным теоретическим инструментом для исследования широкого класса информационных систем.
Широта применимости нового подхода, а именно как параметризации
непараметрических задач, является существенно большей, нежели только для
информационных задач с аддитивным БГШ. Т.е. информационная задача может быть
любой как и не гауссовской, но так, чтобы случайный процесс ![]() аппроксимировался марковским. При этом в
отличие от обычно рассматриваемых, в том числе и в [2], классов непрерывных
(диффузионных) марковских процессов полученные результаты могут быть развиты на
более общие, в том числе на разрывные марковские процессы. Таким образом,
появляется возможность исследования и создания более сложных информационных
систем и прежде всего в системах реального времени. Среди последних
важнейшим является класс перспективнейших информационных систем, работающих в
режимах предсказания (планирования) – экстраполяции. До настоящего времени
развитие таких систем – систем экстраполяции ограничивались именно условиями
фактически гауссовской статистики существующих методов проектирования
стохастических (информационных) систем. В то время как в информационных системах
экстраполяции имеет место ярко выраженная не гауссовская, в общем случае –
непараметрическая, статистика.
аппроксимировался марковским. При этом в
отличие от обычно рассматриваемых, в том числе и в [2], классов непрерывных
(диффузионных) марковских процессов полученные результаты могут быть развиты на
более общие, в том числе на разрывные марковские процессы. Таким образом,
появляется возможность исследования и создания более сложных информационных
систем и прежде всего в системах реального времени. Среди последних
важнейшим является класс перспективнейших информационных систем, работающих в
режимах предсказания (планирования) – экстраполяции. До настоящего времени
развитие таких систем – систем экстраполяции ограничивались именно условиями
фактически гауссовской статистики существующих методов проектирования
стохастических (информационных) систем. В то время как в информационных системах
экстраполяции имеет место ярко выраженная не гауссовская, в общем случае –
непараметрическая, статистика.
Следует отметить, что теоретически предлагаемую процедуру параметризации (условно-параметричекий метод – робастные процедуры) можно спроецировать как статистически, так и в множественно-теоретическом аспекте – топологически [2].
3. Оптимальный и слабый робастные критерии непараметрического обнаружения
Условия априорной нечувствительности в предлагаемом условно-параметрическом методе решения данных непараметрических задач можно получить на основе функции влияния теории робастных статистик [3]. Как отмечено в [3], методика робастных оценок, в том числе на основе функции влияния, имеет параметрический характер, что также хорошо согласуется с предлагаемым условно-параметрическим методом.
Робастные качества
нелинейных алгоритмов, использующих ограниченную выборку, удобно анализировать,
ограничиваясь некоторой окрестностью
![]() изменения
основного распределения
изменения
основного распределения
![]() , например,
окрестностью «загрязнения» - моделью больших ошибок
, например,
окрестностью «загрязнения» - моделью больших ошибок
где ![]() - пространство всех
выборочных распределений.
- пространство всех
выборочных распределений.
Можно использовать аналитические способы введения окрестностей, которые, в отличие от окрестности «загрязнения», являются окрестностями в соответствующих слабых топологиях. Однако использование окрестности «загрязнения» позволяет получить функцию влияния для данного типа задач в достаточно компактном виде.
Например,
непараметрическую задачу обнаружения как задачу распознавания непараметрически
заданной гипотезы
![]() (наличие
сигнала) от простой гипотезы
(наличие
сигнала) от простой гипотезы ![]() (отсутствие сигнала) можно
рассматривать как формирование статистики
(отсутствие сигнала) можно
рассматривать как формирование статистики ![]() в окрестности
в окрестности ![]() в пространстве
выборочных распределений; в общем случае это формирование статистики на основе
нелинейного функционала для наблюдаемой смеси
в пространстве
выборочных распределений; в общем случае это формирование статистики на основе
нелинейного функционала для наблюдаемой смеси
![]() , где
, где ![]() - детерминированный
ограниченный нелинейный оператор. При этом по критерию Неймана – Пирсона в
качестве статистики примем выборочное значение вероятности правильного
обнаружения
- детерминированный
ограниченный нелинейный оператор. При этом по критерию Неймана – Пирсона в
качестве статистики примем выборочное значение вероятности правильного
обнаружения ![]() при заданном уровне
значимости
при заданном уровне
значимости ![]() .
.
В теории робастных
статистик при определении воздействия на статистику (оценку) ![]() распределения
распределения
![]() дополнительного
одного выделяющегося наблюдения
дополнительного
одного выделяющегося наблюдения ![]() широкое применение
получила эвристическая функция влияния [3], которая на основе (3.1) может быть
записана как
широкое применение
получила эвристическая функция влияния [3], которая на основе (3.1) может быть
записана как
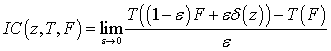 ,
(3.2)
,
(3.2)
где ![]() имеет единичную массу
для выделяющегося наблюдения
имеет единичную массу
для выделяющегося наблюдения ![]() .
.
Эту функцию можно применить для получения робастных критериев задач обнаружения.
В подобных
непараметрических задачах подлежат обнаружению квазидетерминированные сигналы ![]() принадлежащие множеству сигналов S
принадлежащие множеству сигналов S![]() D , у которых имеются неизвестные параметры
D , у которых имеются неизвестные параметры ![]() (
(![]() - ограниченное множество
гильбертового пространства так, что
- ограниченное множество
гильбертового пространства так, что ![]() ). Введем понятие базового сигнала, имеющего
смысл базовой опорной функции, параметры которой обозначаются также как базовые,
т.е.
). Введем понятие базового сигнала, имеющего
смысл базовой опорной функции, параметры которой обозначаются также как базовые,
т.е. ![]() . В дискретном аналоге
наблюдения
. В дискретном аналоге
наблюдения ![]() , т.е. в
последовательности
, т.е. в
последовательности
![]() , может быть
одно или несколько выделяющихся наблюдений
, может быть
одно или несколько выделяющихся наблюдений ![]() . Подобные выделяющиеся
наблюдения могут являться следствием как аномальных значений шума (хвосты
распределений), так неизвестных комбинаций базовых параметров сигнала.
. Подобные выделяющиеся
наблюдения могут являться следствием как аномальных значений шума (хвосты
распределений), так неизвестных комбинаций базовых параметров сигнала.
Тогда функция влияния для
статистики – выборочной вероятности правильного обнаружения ![]()
![]() в точке
в точке ![]() может быть записана как:
может быть записана как:
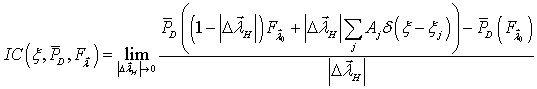 . (3.3)
. (3.3)
В этом выражении ![]() - вектор значений
параметров сигнала для исходного распределения
- вектор значений
параметров сигнала для исходного распределения
![]() , т.е.,
значения параметров базового сигнала
, т.е.,
значения параметров базового сигнала ![]() ,
, ![]() ,
, ![]() - нормированное приращение векторного
параметра так, что
- нормированное приращение векторного
параметра так, что ![]() (
(![]() диагональная матрица),
диагональная матрица), ![]() определяет размер окрестности
определяет размер окрестности![]() ).
).
Достаточно формально в
выражениях (3.3) можно перейти к мере ![]() , которая согласно (3.1) находится в
окрестности
, которая согласно (3.1) находится в
окрестности ![]() и также является мерой
слабой топологии. Поэтому в окрестности
и также является мерой
слабой топологии. Поэтому в окрестности ![]() в точке
в точке ![]() функцию влияния для функционала
функцию влияния для функционала ![]() можно записать в виде
производной по Гато, масштабируемой при разнормировке приращений параметров.
можно записать в виде
производной по Гато, масштабируемой при разнормировке приращений параметров.
В выражении (3.3)
функционалы выборочных вероятностей правильного обнаружения можно выразить с
помощью соответствующих выборочных плотностей распределения вероятностей (оценок
ПРВ -![]() ) следующим образом:
) следующим образом:
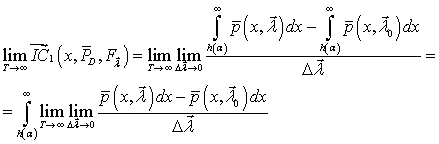 .
.
И после предельного перехода для функции влияния следует
![]()
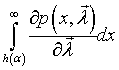 . (3.4)
. (3.4)
Здесь ![]() - значение порога для
случайной величины
- значение порога для
случайной величины ![]() при различении альтернативы
при различении альтернативы
![]() против простой
гипотезы
против простой
гипотезы ![]() при заданном уровне значимости
при заданном уровне значимости ![]() .
.
Очевидно, что при оптимальной робастности (здесь трактовка оптимальной робастности отличается от используемой в [3]) для выражения (3.4) должны выполняться условия (критерий оптимального робастного обнаружения)
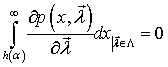 .
.
Применение критерия оптимального робастного обнаружения предполагает существование распределений, которые могут и получены для разрывных марковских процессов в момент принятия решения в соответствующих алгоритмах.
Из условий оптимальной робастности следуют более слабые условия робастности (слабый робастный критерий непараметрического обнаружения – слабые условия)
Очевидно, что при выполнении слабых условий (3.5) критерий оптимального робастного обнаружения будет также выполняться.
Примеры решения непараметрических задач показали, например, [2], что в большинстве практических случаев в нелинейных алгоритмах обработки сигналов применение полученного робастного критерия обнаружения более эффективно в виде слабых условий.
В реализуемых нелинейных алгоритмах системы дифференциальных уравнений удобнее представлять в соответствующей общей форме стохастических дифференциальных уравнений согласно, например, [4], как
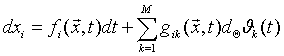 ,
, ![]() , (3.6)
, (3.6)
где ![]() - нелинейные
детерминированные функции, удовлетворяющие условию Липшица,
- нелинейные
детерминированные функции, удовлетворяющие условию Липшица, ![]() -винеровский процесс со
спектральной плотностью
-винеровский процесс со
спектральной плотностью ![]() /2,
/2, ![]() -дифференциал (
-дифференциал (![]() ),
определяющий соответствующие формы записи стохастических дифференциальных
уравнений.
),
определяющий соответствующие формы записи стохастических дифференциальных
уравнений.
Согласно теореме Дуба [4] стохастическая система (3.6) описывает многомерный
марковский диффузионный процесс ![]() , для которого можно записать локальные
характеристики, общая форма которых в обозначениях (3.6) и для
квазидетерминированных сигналов
, для которого можно записать локальные
характеристики, общая форма которых в обозначениях (3.6) и для
квазидетерминированных сигналов ![]() имеет вид
имеет вид
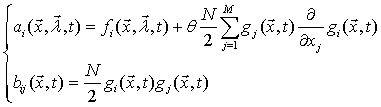 (3.7)
(3.7)
и для системы (3.6) можно
записать уравнение ФПК типа (2.6) для соответствующей нестационарной
плотности ![]() в виде
в виде
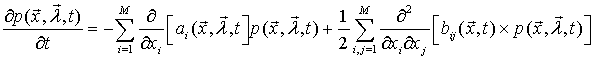 . (3.8)
. (3.8)
Условия (3.7) отражают, во-первых,
зависимость коэффициентов сноса от сигнала ![]() и его параметров
и его параметров ![]() и независимость
коэффициентов диффузии от сигнала, во-вторых, инвариантность коэффициентов по
форме записи уравнений относительно параметров сигнала. Последнее определяется
тем, что в (3.7) от
и независимость
коэффициентов диффузии от сигнала, во-вторых, инвариантность коэффициентов по
форме записи уравнений относительно параметров сигнала. Последнее определяется
тем, что в (3.7) от ![]() зависят только первые
слагаемые коэффициентов сноса.
зависят только первые
слагаемые коэффициентов сноса.
Для окончательного
структурно-параметрического синтеза алгоритмов обработки используются слабые
условия робастности (3.5) для любого момента времени, в том числе для
![]() , в виде
, в виде
![]() ,
, 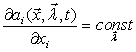
![]() , что соответствует
системе уравнений
, что соответствует
системе уравнений
![]()
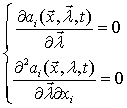 . (3.9)
. (3.9)
Однако для реальных задач система (3.9) может быть системой уравнений только в асимптотическом смысле, например, при соответствующей нормировке каждого из выражений системы. Тогда систему уравнений (3.9) можно записать в форме линейных дифференциальных уравнений (ЛДУ) для коэффициентов сноса уравнения ФПК как
 , (3.10)
, (3.10)
где ![]() - нормирующие коэффициенты.
- нормирующие коэффициенты.
Уравнения (3.10) после
дифференцирования по ![]() становится
однородными линейными дифференциальными уравнениями (ОЛДУ) для нелинейных
параметров стохастического ДУ. И для принятой марковской модели ОЛДУ имеют
первый порядок, решения которых при постоянных
становится
однородными линейными дифференциальными уравнениями (ОЛДУ) для нелинейных
параметров стохастического ДУ. И для принятой марковской модели ОЛДУ имеют
первый порядок, решения которых при постоянных ![]() имеют экспоненциальный
характер, поэтому параметрические зависимости для коэффициентов НДУ являются
существенно нелинейными.
имеют экспоненциальный
характер, поэтому параметрические зависимости для коэффициентов НДУ являются
существенно нелинейными.
Таким образом, алгоритмы обработки, по крайней мере в данном классе диффузионных
марковских процессов, в непараметрических задачах должны быть реализованы в виде
существенно нелинейных дифференциальных уравнений. Например, для следящих
полосовых фильтров алгоритм обработки может быть реализован в виде НДУ третьего
порядка [2], а в случае когерентных следящих систем синтезируются системы
частотной или фазовой автоподстройки высокого порядка [6].
4. Синтез адаптивного фильтра (обнаружителя одиночного радиоимпульса)
При приеме на фоне шума предложенным условно-параметрическим
методом может решаться задача обнаружения радиоимпульса, распределение несущей
частоты ![]() которого принадлежит некоторому
ограниченному непараметризированному семейству в диапазоне частот
которого принадлежит некоторому
ограниченному непараметризированному семейству в диапазоне частот ![]() Т.е. наблюдается действительный случайный
процесс
Т.е. наблюдается действительный случайный
процесс
![]() (4.1)
(4.1)
Здесь
![]() - известный
амплитудный множитель, определяющий мощность радиоимпульса;
- известный
амплитудный множитель, определяющий мощность радиоимпульса;
![]() - случайная
начальная фаза с равномерным распределением на интервале
- случайная
начальная фаза с равномерным распределением на интервале ![]() ,
, ![]() - функция огибающей радиоимпульса,
причем
- функция огибающей радиоимпульса,
причем ![]() ;
; ![]() вектор как известных, так и неизвестных
параметров огибающей так, что
вектор как известных, так и неизвестных
параметров огибающей так, что ![]() множеству соответствующего эвклидового
пространства, например, для прямоугольной огибающей
множеству соответствующего эвклидового
пространства, например, для прямоугольной огибающей ![]() и
и ![]() (
(![]() соответственно начальное положение
и длительность радиоимпульса);
соответственно начальное положение
и длительность радиоимпульса);
![]() случайная
величина,
случайная
величина, ![]() может быть БГШ с нулевым средним
и интенсивностью
может быть БГШ с нулевым средним
и интенсивностью
![]() , или
какой-либо другой шум,
, или
какой-либо другой шум, ![]() - время наблюдения.
- время наблюдения.
По результатам наблюдения должно приниматься решение об
отсутствии сигнала: гипотеза
![]() или его
наличии – непараметрически заданная гипотеза
или его
наличии – непараметрически заданная гипотеза ![]() , так как в данной задаче
обрабатываемый сигнал имеет случайную частоту и другие параметры с неизвестными
распределениями, а также оценка этих параметров.
, так как в данной задаче
обрабатываемый сигнал имеет случайную частоту и другие параметры с неизвестными
распределениями, а также оценка этих параметров.
Обнаружение квазидетерминированного сигнала ![]() проводится на основе использования слабого
робастного критерия непараметрического обнаружения (3.5). А именно, к
наблюдениям (4.1) применяется преобразование в виде нелинейного сглаживающего
оператора
проводится на основе использования слабого
робастного критерия непараметрического обнаружения (3.5). А именно, к
наблюдениям (4.1) применяется преобразование в виде нелинейного сглаживающего
оператора ![]() . Поэтому на интервале
наблюдения можно записать функционал
. Поэтому на интервале
наблюдения можно записать функционал
![]()
и алгоритм работы подобного нелинейного обнаружителя представить в виде
где
![]() - порог
обнаружения при заданном
- порог
обнаружения при заданном ![]() и нелинейный
сглаживающий оператор эвристически как нелинейный дифференциальный оператор типа
и нелинейный
сглаживающий оператор эвристически как нелинейный дифференциальный оператор типа
![]() , (4.3)
, (4.3)
где
![]() -
детерминированные нелинейные функции своих аргументов,
удовлетворяющие условиям Липшица,
-
детерминированные нелинейные функции своих аргументов,
удовлетворяющие условиям Липшица, ![]() некоторые целые числа,
определяющие структуру оператора.
некоторые целые числа,
определяющие структуру оператора.
Выбор структуры нелинейного дифференциального оператора
(первоначальный структурный синтез линейного прототипа - базовой структуры)
проводится по критерию согласованности [2] и опорным функциям, использующим
априорную информацию о нестационарном случайном процессе (НСППР) ![]() , а именно, соответствующие моментные
функции, например, математические ожидания. Критерий согласованности имеет вид
, а именно, соответствующие моментные
функции, например, математические ожидания. Критерий согласованности имеет вид
где
![]()
![]() - опорная функция,
- опорная функция, ![]() - вектор известных параметров (
- вектор известных параметров (![]() );
); ![]() - импульсная характеристика (ИХ),
определяемая на луче (0,
- импульсная характеристика (ИХ),
определяемая на луче (0,![]() ), физически реализуемого линейного
фильтра, соответствующего нелинейному оператору (9.1.4) при
), физически реализуемого линейного
фильтра, соответствующего нелинейному оператору (9.1.4) при ![]() ;
;
![]() нормирующий
коэффициент;
нормирующий
коэффициент; ![]() - временной параметр,
определяющий,
- временной параметр,
определяющий,
![]() а именно,
временной параметр оператора запаздывания.
а именно,
временной параметр оператора запаздывания.
Слабый робастный критерий непараметрического обнаружения запишем в виде
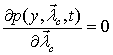 , (4.5)
, (4.5)
где
![]() одномерная
плотность распределения вероятностей (ПРВ) для функционала
одномерная
плотность распределения вероятностей (ПРВ) для функционала ![]() в текущий момент времени
(для обнаружителя (4.2) при
в текущий момент времени
(для обнаружителя (4.2) при ![]() ).
).
Полный синтез нелинейного робастного алгоритма обработки для задачи (4.2) проводится на основе критерия (4.5) с учетом результатов первоначального структурного синтеза.
Особенность данной задачи заключается в выборе соответствующей опорной функции. Как известно, квазигармонические (узкополосные) НСППР могут быть записаны как (что и является в реальных задачах фактически единственной априорной информацией)
![]() ,
(4.6)
,
(4.6)
где
![]() - некоторая
известная или неизвестная средняя частота;
- некоторая
известная или неизвестная средняя частота; ![]() - медленные случайные процессы,
имеющие для непараметрических задач произвольные распределения.
- медленные случайные процессы,
имеющие для непараметрических задач произвольные распределения.
При решении задачи (4.2) для НСППР (4.6) опорные функции ![]() (
(![]() ,
, ![]() известные параметры опорной функции
известные параметры опорной функции ![]() ) могут быть получены на основе
корреляционных свойств подобных НСППР. Для этого для реализаций
) могут быть получены на основе
корреляционных свойств подобных НСППР. Для этого для реализаций
![]() на некотором
фиксированном интервале введем усредненную автокорреляционную функцию (УАКФ)
на некотором
фиксированном интервале введем усредненную автокорреляционную функцию (УАКФ)
Здесь
и ниже ![]() текущее начало координат. Подобный алгоритм
и может быть эффективно использован для первоначального обнаружения и
оценки некоторых параметров неизвестного сигнала. Далее, приняв
текущее начало координат. Подобный алгоритм
и может быть эффективно использован для первоначального обнаружения и
оценки некоторых параметров неизвестного сигнала. Далее, приняв ![]() , запишем УАКФ, используя для
, запишем УАКФ, используя для ![]() разложение
Карунена-Лоэва в виде
разложение
Карунена-Лоэва в виде
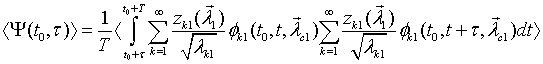 , (4.7)
, (4.7)
где
![]() часть
существенных случайных параметров, которые могут соответствующим образом
характеризовать собственные функции.
часть
существенных случайных параметров, которые могут соответствующим образом
характеризовать собственные функции.
Опорная функция ![]() соответственно определяется АКФ (4.7) как
соответственно определяется АКФ (4.7) как
 . (4.8)
. (4.8)
Таким образом, опорные функции квазигармонических НСППР определяются по (4.8).
Наблюдаемый радиоимпульс с детерминированной огибающей,
неизвестной частотой ![]() и равномерно распределенной
начальной фазой
и равномерно распределенной
начальной фазой ![]() на основе представления (4.7) можно
записать в виде (индекс «
на основе представления (4.7) можно
записать в виде (индекс «![]() » для
» для ![]() указывает на процедуру
параметризации)
указывает на процедуру
параметризации)
![]()
![]() .
.
Корреляционная функция подобного случайного процесса (СП) равна
![]() , где
, где  .
.
Тогда,
а также на основе выражения (4.8),опорная функция СП ![]() равна
равна
![]() ,
, ![]() , (4.9)
, (4.9)
где
![]() произвольная
начальная фаза, так как алгоритм определения опорной функции через
корреляционную функцию квазигармонического случайного процесса, т.е.
произвольная
начальная фаза, так как алгоритм определения опорной функции через
корреляционную функцию квазигармонического случайного процесса, т.е. ![]() , является инвариантным
к начальной фазе. Эта инвариантность и является основой для развития алгоритма
(4.6а) как многомерного и результативного для получения грубых (первоначальных)
оценок.
, является инвариантным
к начальной фазе. Эта инвариантность и является основой для развития алгоритма
(4.6а) как многомерного и результативного для получения грубых (первоначальных)
оценок.
В простейшем случае, те при обработке радиоимпульса с простейшей огибающей, в опорной функции (4.9) используются два типа временных зависимостей огибающей:
а) ![]() б)
б) ![]()
![]() . (4.10)
. (4.10)
Здесь
![]() - параметры,
определяемые из условия единичной нормы временных функций.
- параметры,
определяемые из условия единичной нормы временных функций.
Согласно выражению (4.4) и опорной функции (4.9) несложно
получить, что импульсная характеристика соответствующей базовой параметрической
структуры будет иметь вид ![]() , где
, где ![]() - постоянная времени,
- постоянная времени, ![]() - начальная фаза, определяемая
параметрами
- начальная фаза, определяемая
параметрами ![]() в (4.7) и
в (4.7) и ![]() в (4.8),
в (4.8), ![]() - текущая частота, как
функция управляющего воздействия -
- текущая частота, как
функция управляющего воздействия -
![]() собственных
колебаний контура; для (4.10) соответственно
собственных
колебаний контура; для (4.10) соответственно
![]() или
или
![]() .
.
Таким образом, состояние базовой структуры в данной задаче описывается линейным дифференциальным уравнением (ЛДУ) второго порядка с переменными коэффициентами, а изменение коэффициентов задается системой управления, которая описывается, например, в виде ЛДУ первого порядка с постоянными коэффициентами. Тогда нелинейный алгоритм обработки в виде системы стохастических нелинейных дифференциальных уравнений может быть записан
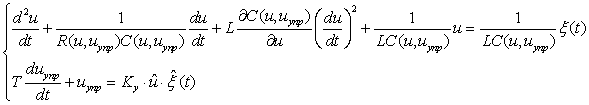 (4.11)
(4.11)
Здесь
![]() - нелинейные
соответственно сопротивление и ёмкость ОКК,
- нелинейные
соответственно сопротивление и ёмкость ОКК, ![]() и индуктивность может быть принята
как постоянная,
и индуктивность может быть принята
как постоянная, ![]() - сопряженные по
Гильберту соответственно случайные процессы для
- сопряженные по
Гильберту соответственно случайные процессы для ![]() и
и ![]() ,
, ![]() - соответственно сопротивление и
емкость интегрирующей электрической цепи первого порядка как ФНЧ,
- соответственно сопротивление и
емкость интегрирующей электрической цепи первого порядка как ФНЧ, ![]() коэффициент передачи перемножителя.
коэффициент передачи перемножителя.
Перейдя в системе уравнений (4.11) от ![]() в
точке
в
точке ![]() (
(![]() текущая частота) к задержанному сигналу
текущая частота) к задержанному сигналу ![]() ,
, ![]() ,где
,где ![]() - текущая постоянная контура,
причем
- текущая постоянная контура,
причем ![]() , так как
, так как ![]() ,
систему (4.11) можно записать в симметризированной форме как (обозначив
,
систему (4.11) можно записать в симметризированной форме как (обозначив ![]() )
)
Для окончательного структурно-параметрического синтеза, в том
числе для определения параметрических зависимостей
![]() можно
использовать слабый критерий робастного обнаружения в виде
можно
использовать слабый критерий робастного обнаружения в виде
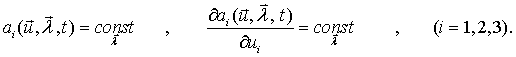 (4.13)
(4.13)
Согласно методики [2] из системы уравнений (4.12) можно получить следующие выражения для коэффициентов сноса:
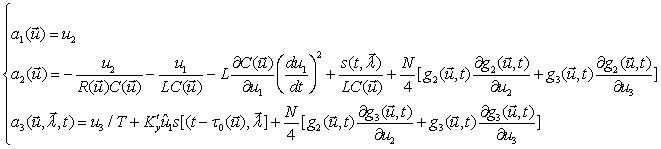 ,
(4.14)
,
(4.14)
где ![]() ,
, ![]() .
.
Применив для коэффициентов (4.14) условия (4.13) можно получить, разложив
функцию ![]()
![]() в точке
в точке ![]() по малому параметру
по малому параметру ![]() и учтя малые члены
первого порядка малости
и учтя малые члены
первого порядка малости
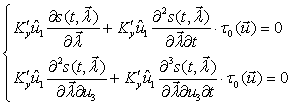 . (4.15)
. (4.15)
Как отмечено выше, вследствие ![]() условия (4.15) могут
выполняться в большинстве практических случаев только асимптотически, т.е. при
попарной соответствующей нормировке обеих выражений в (4.15). Т.е., эти
условия означают также пренебрежение первыми слагаемыми и сохранение только
малых членов. Тогда (4.15) приводятся к системе однородных линейных
дифференциальных уравнений первого порядка
условия (4.15) могут
выполняться в большинстве практических случаев только асимптотически, т.е. при
попарной соответствующей нормировке обеих выражений в (4.15). Т.е., эти
условия означают также пренебрежение первыми слагаемыми и сохранение только
малых членов. Тогда (4.15) приводятся к системе однородных линейных
дифференциальных уравнений первого порядка
 ,
,
где ![]() - нормирующие коэффициенты.
(4.16)
- нормирующие коэффициенты.
(4.16)
Система уравнений (4.16) может быть как совместной, так и независимой. Можно
разрешить систему как совместную (приняв ![]() ) в виде
) в виде
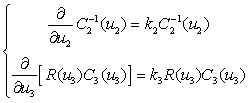 , (4.17)
, (4.17)
где
![]() -
действительные числа.
-
действительные числа.
Из системы (4.17) следует, что сопротивление зависит только от одной переменой состояния алгоритма обработки, описываемого системой (4.12), а емкость – от двух переменных. Таким образом, решение системы (4.17) можно получить, например, в виде
![]() , причем
, причем ![]() . (4.18)
. (4.18)
Здесь
![]() - постоянная
интегрирования, например,
- постоянная
интегрирования, например, ![]() , функция
, функция ![]() ,
, ![]() ,
, ![]() (
(![]() - коэффициент пропорциональности).
- коэффициент пропорциональности).
На рис. 1 приведена принципиальная схема адаптивного робастного фильтра, изображенная согласно системе уравнений (4.11), параметрическим функциональным нелинейным зависимостям и условию (4.18). Подобный адаптивный фильтр является согласно условиям выражения (4.9) некогерентным обнаружителем радиоимпульса.
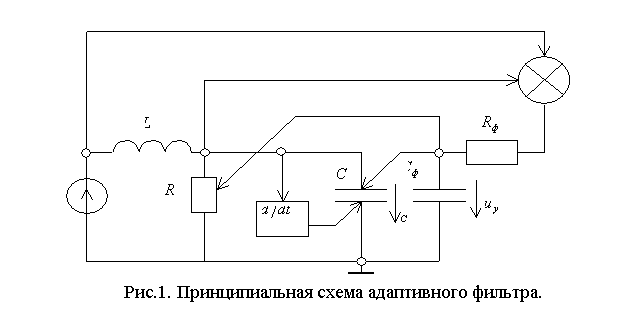
5. Развитие робастных алгоритмов для произвольных помех
Приведенные выше результаты, хотя и являются новыми, однако, относятся, можно так назвать, к диффузионным стохастическим системам. Это прежде всего такие информационные системы, состояние которых описывается диффузионными (непрерывными или гладкими) марковскими процессами. Системы же экстраполяции или предсказания в большей степени ориентированы, более востребованы к разрывным случайным процессам, и подобная ситуация имеет место также для радиотехнических и других информационных систем, когда помехи имеют произвольные, а не гауссовские распределения. Как правило, эти произвольные, априорно неизвестные распределения и будут обуславливать разрывной характер марковских случайных процессов, описывающих состояние функционирующих информационных систем. И среди разнообразных помех в настоящее время все более широкое внимание уделяется помехам, совпадающие по спектру с информационным сигналом.
Примером таких информационных систем, которые могут быть использованы для обработки информации, например, в таких специфических информационных системах как информационно-поисковые, которые в настоящее время строятся, в основном, на принципах корреляционной обработки баз данных.
Для радиолокационных систем подобными являются использующие свехширокополосные сигналы (СШП) [6]. Согласно предлагаемому методу робастной нелинейной фильтрации в этих системах обработки информации в простейших случаях алгоритмы обработки наблюдений могут реализовываться на нелинейных дифференциальных уравнениях первого порядка со случайной правой частью с учетом приведенного выше материала.
В качестве базового сигнала для подобных систем может принят прямоугольный импульс, для которого алгоритм обработки имеет вид следующего стохастического дифференциального уравнения, записанного, например, в форме Ито
 ,
, ![]() . (5.1)
. (5.1)
Здесь ![]() - известная длительность
информационного сигнала
- известная длительность
информационного сигнала ![]() ,
, ![]() - подлежащая определению нелинейная функция,
для которой выполняются условия Липшица. При этом реальный информационный сигнал
имеет мультипликативную помеховую добавку в виде гармонической функции (параметр
- подлежащая определению нелинейная функция,
для которой выполняются условия Липшица. При этом реальный информационный сигнал
имеет мультипликативную помеховую добавку в виде гармонической функции (параметр ![]() ).
).
Синтез функции ![]() проводится с использованием слабых условий
и (5.1):
проводится с использованием слабых условий
и (5.1):
![]()
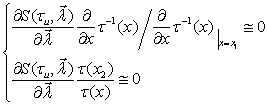 , (5.2)
, (5.2)
![]() -фиксированные точки: подставляются после
соответствующего дифференцирования.
-фиксированные точки: подставляются после
соответствующего дифференцирования.
Так как оба
выражения (5.2) являются безразмерными, то при подборе тождественности из них
следует дифференциальное уравнение для нелинейной функции ![]() , т.е.
, т.е.![]()
![]() , которое имеет решение
, которое имеет решение
![]() (5.3)
(5.3)
В (5.3) ![]() - постоянная интегрирования,
- постоянная интегрирования,
![]() , а точки
, а точки ![]() и
и ![]() выбираются из условия асимптотического
обеспечения (5.2).
выбираются из условия асимптотического
обеспечения (5.2).
Таким образом, согласно
(5.3) следует, что и для данных непараметрических задач алгоритмы обработки
наблюдений должны быть принципиально нелинейными. Следует отметить, что при
определении нелинейной функции ![]() необходимо соблюдение условий Липшица в
уравнении (5.1), иначе будет нарушаться марковость процесса
необходимо соблюдение условий Липшица в
уравнении (5.1), иначе будет нарушаться марковость процесса ![]() , что и было установлено при
моделировании.
, что и было установлено при
моделировании.
Робастность полученных нелинейных алгоритмов можно оценить также с помощью функции М-оценок, например, по методике [3]. Эта функция имеет вид
![]() ,
где
,
где ![]() - некоторая
функция.
(5.4)
- некоторая
функция.
(5.4)
Если
![]() , то
, то ![]() -
оценка максимального правдоподобия (М-оценка).
-
оценка максимального правдоподобия (М-оценка).
Для М-оценок функция влияния выражается через функцию М-оценок и, как показано в [3], функция влияния для функционалов оценок, дифференцируемых по Фреше, может представляться в виде
![]() , где
, где ![]() - функция распределения и
плотность параметрического (многопараметрического) семейства
- функция распределения и
плотность параметрического (многопараметрического) семейства ![]() -информация Фишера.
-информация Фишера.
Т.к. для задач
сдвига, в том числе с минимальной информацией Фишера, ![]() , то функция влияния равна
, то функция влияния равна ![]() (
(![]() - некоторая постоянная) и для М-оценок, т.к.
функция влияния инвариантна к оценке, можно использовать функцию
- некоторая постоянная) и для М-оценок, т.к.
функция влияния инвариантна к оценке, можно использовать функцию
![]() . (5.5)
. (5.5)
Выражение (5.5) позволяет, в том числе и при численном статистическом моделировании, оценить робастные свойства исследуемых нелинейных алгоритмов.
Разработанные нелинейные
алгоритмы экспериментально исследовались статистическим моделированием.
Параметры сигнала и шума выбирались таким образом, чтобы обеспечивалась
состоятельная оценка (объеме статистической выборки -![]() ).
).

Рис. 2. Зависимость вероятности правильного обнаружения нестатистической непараметрической модели от обобщенного параметра.
Результаты статистического
моделирования нелинейных алгоритмов приведены на рис. 2 для двух
функций ![]() с различными степенями
нелинейности: относительно слабая -
с различными степенями
нелинейности: относительно слабая -![]() ,
, ![]() - сильная. На рис. 2 изображены графики
вероятностей правильного обнаружения
- сильная. На рис. 2 изображены графики
вероятностей правильного обнаружения ![]() в зависимости от
обобщенного параметра
в зависимости от
обобщенного параметра ![]() , сдвигающим
распределение шума (кривая 1 соответствует нелинейности
, сдвигающим
распределение шума (кривая 1 соответствует нелинейности
![]() , кривая 2 –
нелинейности
, кривая 2 –
нелинейности
![]() , кривая 3 –
согласованный линейный фильтр). Все графики начинаются из одной точки при
, кривая 3 –
согласованный линейный фильтр). Все графики начинаются из одной точки при ![]() ,
т.е. нелинейный алгоритм формирует распределение с минимальной информацией
Фишера.
,
т.е. нелинейный алгоритм формирует распределение с минимальной информацией
Фишера.
Робастность на основе
функции М–оценок нелинейного алгоритма с нелинейностью
![]() -
-![]() показана на рис.3
(кривая 1) и для линейного согласованного фильтра, который не обладает
робастностью - (кривая 2). Из графика следует, что при
показана на рис.3
(кривая 1) и для линейного согласованного фильтра, который не обладает
робастностью - (кривая 2). Из графика следует, что при ![]() ,
определяющих мощность критерия различения гипотез, график
,
определяющих мощность критерия различения гипотез, график ![]() нелинейного алгоритма прижимается к оси
абсцисс. Таким образом, нелинейный алгоритм снижает влияние больших выбросов у
случайного процесса
нелинейного алгоритма прижимается к оси
абсцисс. Таким образом, нелинейный алгоритм снижает влияние больших выбросов у
случайного процесса ![]() в области нулевой гипотезы, т.е.
имеет ярко выраженную робастность.
в области нулевой гипотезы, т.е.
имеет ярко выраженную робастность.
И очевидно, что наиболее
существенным результатом использования данного нелинейного алгоритма с ярко
выраженной нелинейностью – это его существенные непараметрические
характеристики, т.е. когда критерий качества приближается (стремится) к РНМ
критерию. При этом случайный процесс (и это было установлено при моделировании
[2]) как диффузионный марковский разлаживается, т.е. становится разрывным, так
что в (2.4) ![]()
![]() при
при ![]() .
.
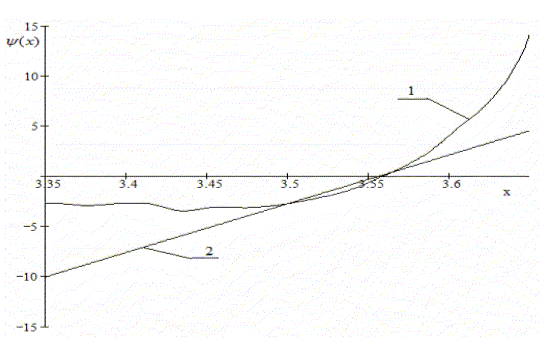
Рис.3. Зависимости функции М-оценок нелинейного и линейного алгоритмов.
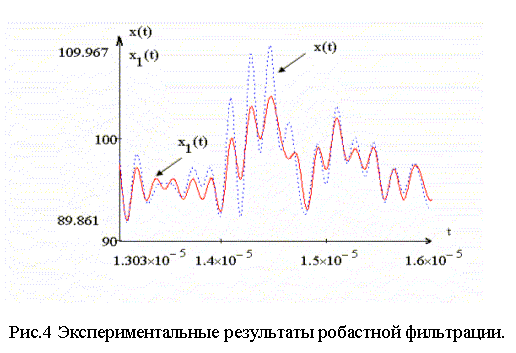
Результаты экспериментальных исследований обработки реальных, но уже
узкополосных сигналов приведены на рис.4, из которого следует, что
робастная обработка при данных, также совпадающих по спектру сигналов и шумов и
некоторой конкретной выборки увеличивает отношение сигнал/шум примерно на
10дб. На рисунке принято x(t)-обработанное,
x1(t)-необработанное наблюдения. По оси абсцисс указаны масштабы
реального времени наблюдения конкретной цели, а по оси ординат текущие величины
выходного устройства наблюдения.
Предельные оценки, которые для
подобной обработки могут быть и более значительны, приведены в [2].
Список литературы
1. Теория обнаружения сигналов/П.С. Акимов, П.А. Бакут, В.А. Богданович и др., : Под
редакцией П.А. Бакута. - М: Радио и связь, 1984 - 440с.
2. Неволин В.И. Робастные информационные системы. Методы синтеза и анализа. – М.: Радио и связь, 2008. – 312с.: ил.
3.Хьюбер Дж., Робастность в статистике. Пер. с англ. М.: Наука, 1984.
4. Тихонов В.И., Миронов М.А. Марковские процессы. - М.: Советское радио, 1977.
5. Левин Б.Р., Теоретические основы статистической радиотехники в 3-х кн. - М.: Советское радио, 1976. - Кн.3. - 285с.
6. Помехозащищенность систем радиосвязи с расширением спектра сигналов модуляцией псевдослучайной последовательностью.//В.И.Борисов, В.М.Зинчук, А.Е.Лимарев, Н.П.Мухин, Г.С.Нахамсон; Под ред. В.И.Борисова.- М.: Радио и связь, 2003.
 ,
(2.6)
,
(2.6)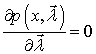 или
или 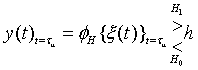 ,
, 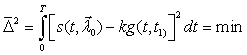 , (4.4)
, (4.4) .
(4.6а)
.
(4.6а) . (4.12)
. (4.12)