УДК 535.44

ФОРМИРОВАНИЕ ЗАМОРОЖЕННОЙ МОДЫ k⁴

 

А. И. Игнатов, А. М. Мерзликин, А. П. Виноградов

Институт Теоретической и Прикладной Электродинамики РАН

 

Получена 4 января 2011 г.

 

Аннотация. Рассмотрены условия, при которых для одномерного фотонного кристалла формируется замороженная мода вблизи стационарной точки ω~k⁴_Bl дисперсионной кривой. В работе показано, что данный вид замороженной моды формируется на частоте касания границ бриллюэновской и вырожденной запрещенных зон.

Ключевые слова: замороженная мода, запрещенные зоны фотонных кристаллов.

Abstract. Conditions of the formation of the frozen mode near the stationary point ω~k⁴_Bl of a dispersion relation are analyzed in case of a 1D photonic crystal. It is shown that the frozen mode of this type forms at the frequency of the contact of boundaries of Brillouin and degenerate band gaps.

Key words: frozen mode, photonic crystal band gaps.

Введение.

В настоящее время очень бурно развивается оптика сред, электродинамические параметры которых меняются периодически в пространстве на расстояниях порядка длины волны – фотонных кристаллов (ФК). Такие среды могут обладать свойствами, которые либо вообще не проявляются в однородных средах, либо проявляются значительно слабее: наличие запрещенных зон в спектре [1,2], оптический аналог эффекта Боррманна [2], отрицательное преломление [2], эффект суперпризмы [2] и т.д. В частности активно изучаются ФК, материалы которых обладают анизотропией либо гиротропией [3-28]. Интерес к таким ФК обусловлен их различными оптическими свойствами в зависимости от поляризации света, возможностью управлять этими свойствами с помощью постоянного внешнего магнитного [17,25,28] и электрического [19] полей, эффектами невзаимности, которые невозможны в ФК из оптически изотропных немагнитных материалов [9,11], и т.д.

Одна из особенностей ФК из анизотропных и гиротропных материалов – возможность формирования замороженной моды [7-9]. Замороженная мода формируется на так называемой вырожденной границе запрещенной зоны. Это такая граница  запрещенной зоны, в окрестности которой дисперсионная зависимость описывается параболой 4-й степени  [7,8]. Очевидно, что вблизи вырожденной границы групповая скорость волн в ФК близка к нулю. Однако замороженная мода отличается от решения вблизи границы обыкновенной бриллюэновской запрещенной зоны (ЗЗ) тем, что амплитуда замороженной моды внутри ФК достигает значений, на несколько порядков превосходящих амплитуду падающей на ФК волны.  

Подробный анализ свойств замороженных мод проведен в работах [7-10]. Однако вопрос о самом существовании необходимых для возникновения замороженных мод особенностей дисперсионных зависимостей, а также о достаточных условиях, при которых эти особенности реализуются, остался открытым.

Данная работа посвящена изучению достаточных условий образования вырожденной границы запрещенной зоны, вблизи которой

                                                                                          (1)

и формируется замороженная мода.

Мы будем рассматривать лишь нормальное падение волн на одномерные ФК.

Формирование вырожденной границы ЗЗ. Качественные рассуждения.

Отметим, что четвертая степень в зависимости (1) вблизи вырожденной границы ЗЗ – максимальная из возможных для стационарных точек дисперсионных зависимостей в ФК. Это непосредственно следует из того, что дисперсионное соотношение произвольного ФК является полиномом четвертой степени от  ( – период ФК) и что каждой частоте соответствует четыре блоховских волновых числа (учитывая как волны, распространяющиеся с положительной, так и волны с отрицательной фазовой скоростью), лежащих в приведенной зоне Бриллюэна [21,9]. Поэтому вырожденная граница ЗЗ является такой точкой, в которой сходятся все дисперсионные кривые при данной частоте. Следовательно, надо ожидать, что вырожденная граница ЗЗ будет возникать в таких ФК и на таких частотах, где достигается наибольшая вырожденность по решениям дисперсионного уравнения (здесь следует повторить, что вырожденная ЗЗ не может формироваться в одномерных ФК только из изотропных немагнитных материалов [7]). Из этих качественных рассуждений следует, что подходящими кандидатами в вырожденные границы могли бы быть точки, являющиеся одновременно границей вырожденной [28] и бриллюэновской ЗЗ. Действительно, на частотах вырожденной ЗЗ действительные части всех четырех блоховских волновых чисел равны с точностью до знака [28], а на границах вырожденной ЗЗ с точностью до знака равны и сами блоховские волновые числа. Если рассматриваемая частота является еще и границей бриллюэновской ЗЗ, все четыре блоховских волновых числа выйдут на границу зоны Бриллюэна, а значит, ввиду инвариантности дисперсионных кривых относительно трансляции на вектор обратной решетки, будут равны между собой. Поэтому мы будем рассматривать ФК, в которых на некоторой частоте реализуется одновременно граница вырожденной и бриллюэновской ЗЗ.

Формирование и свойства вырожденных запрещенных зон.

Прежде чем продолжить изучение вырожденной границы ЗЗ, расскажем подробнее о причинах возникновения вырожденных ЗЗ [28], их свойствах. В работах [20,21] было впервые показано, что в одномерных ФК из одноосного материала с периодически меняющейся от слоя к слою ориентацией оптических осей (в плоскости слоев) возможно появление особого типа запрещенных зон, не на границе, а внутри зон Бриллюэна. В [26-28] показано, что подобного рода ЗЗ возможны и в анизотропных ФК с постоянным направлением осей анизотропии, но при наличии гиротропных компонент. ЗЗ первого (анизотропные) [21] и второго (гиротропные) [28] типа обладают отличительным свойством – они являются общими для волн любой поляризации, внутри таких ЗЗ действительная и мнимая части волнового вектора не зависят (с точностью до знака) от поляризации волны [28]. Поэтому мы будем их называть вырожденные ЗЗ.

Рассмотрим формирование вырожденной ЗЗ на примере анизотропной вырожденной ЗЗ в ФК со слоями из одноосного материала. Ориентация оптических осей слоев меняется периодически от слоя к слою (в плоскости слоев) (см. рис. 1).

 

Рис. 1. Одномерный слоистый ФК со слоями из оптически одноосного материала. Жирными стрелками показаны ориентации оптических осей слоев (в плоскости слоев). Стрелка слева – волновой вектор падающей волны.

 

Если предположить вначале, что оптические оси всех слоев сонаправлены, то блоховские волны будут иметь фиксированную поляризацию (либо обыкновенную, либо необыкновенную). Каждая блоховская волна не чувствует анизотропии слоев ФК. Вырожденная ЗЗ не возникает.

 

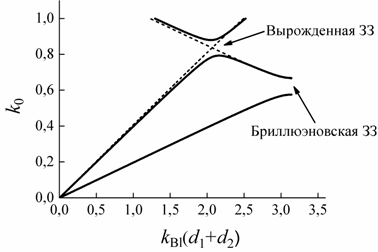
Рис. 2. Сплошные линии - дисперсионные кривые анизотропного ФК с отклонением между ориентациями осей анизотропии слоев, пунктирные – при сонаправленных оптических осях слоев.

 

На рис. 2 пунктирные линии – дисперсионные кривые блоховских волн в этом случае.

Если теперь отклонить оптические оси слоев друг от друга (в плоскости слоев), то при отражении и при прохождении через границы слоев обыкновенная волна сможет переходить в необыкновенную (и наоборот). Таким образом, в блоховской волне обыкновенная и необыкновенная компоненты оказываются гибридизованными. В этом случае возникает вырожденная ЗЗ (см. сплошные кривые на рис. 2) на частотах вблизи пересечения дисперсионных ветвей [21]. На этих частотах осуществляется брэгговское отражение от элементарной ячейки, при котором волна, проходящая через элементарную ячейку, в одном направлении приобретает набег фаз, соответствующий обыкновенному показателю преломления, а в обратном направлении – набег фаз, соответствующий необыкновенному показателю преломления. Аналогично формируется и гиротропная вырожденная ЗЗ в анизотропном ФК, оптические оси всех слоев которого сонаправлены. В этом случае гибридизация обыкновенной и необыкновенной компонент вызвана вращением плоскости поляризации в гиротропных слоях. Гиротропные вырожденные ЗЗ также формируются на частотах в окрестности пересечения дисперсионных кривых [28].

         Отметим, что вырожденная ЗЗ может формироваться не только вдали от бриллюэновских ЗЗ, но также и на частотах, принадлежащих бриллюэновской ЗЗ. Такое оказывается возможным, если частотные области бриллюэновских ЗЗ разных поляризаций пересекаются.

         Действительно, вернемся к анизотропному ФК, рассмотренному нами выше (см. рис. 1). Если предположить вначале, что оптические оси всех слоев сонаправлены, блоховские волны будут иметь определенную поляризацию – обыкновенную (перпендикулярную оптическим осям) и необыкновенную (параллельную оптическим осям). Дисперсионные ветви (частотные зависимости действительной и мнимой компонент блоховского волнового вектора), соответствующие каждой из этих блоховских волн, изображены на рис. 3. Здесь видно, что бриллюэновские ЗЗ, соответствующие разным блоховским волнам, пересекаются. Однако ввиду независимости обыкновенной и необыкновенной волн в случае параллельных оптических осей слоев вырожденная ЗЗ не возникает. На рис. 3 приведены результаты расчетов для ФК с периодом  из двух слоев одинаковой толщины .  - блоховское волновое число,  - волновое число в вакууме. Параметры первого слоя: обыкновенная диэлектрическая проницаемость , необыкновенная - . Параметры второго слоя: обыкновенная диэлектрическая проницаемость , необыкновенная - .

 

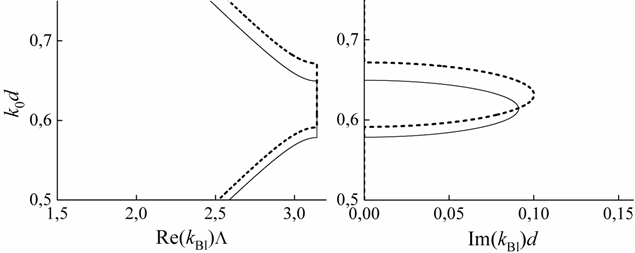
Рис. 3. Дисперсионные кривые двух блоховских волн в анизотропном ФК с сонаправленными оптическими осями слоев. Бриллюэновские ЗЗ пересекаются. Однако, ввиду отсутствия гибридизации обыкновенной и необыкновенной волн, вырожденная ЗЗ не возникает. Параметры ФК приведены в тексте.

 

Если теперь отклонить оптические оси слоев периода на некоторый угол друг от друга (в плоскости слоев), то обыкновенная и необыкновенная поляризации оказываются гибридизованными в каждой из блоховских гармоник. На пересечении дисперсионных ветвей (действительной и мнимой компонент) может образоваться вырожденная ЗЗ (см. рис. 4). На рис. 4 приведены результаты для ФК с теми же параметрами слоев, что и в случае рис. 3, однако оптические оси слоев отклонены друг от друга на угол 0,08 рад. Видно, что теперь, ввиду гибридизации обыкновенной и необыкновенной волн, на пересечении двух бриллюэновских ЗЗ возникает вырожденная ЗЗ. На частотах вырожденной ЗЗ мнимые части блоховских волновых чисел разных ветвей равны (с точностью до знака). Действительные части также равны (с точностью до знака), однако они лежат уже не на границе зоны Бриллюэна, как у бриллюэновской ЗЗ, а внутри.

 

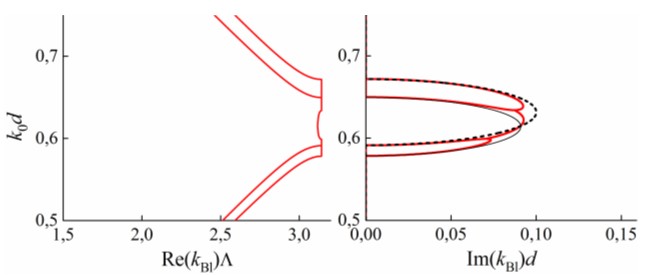
Рис. 4. Дисперсионные кривые (красные) в ФК с теми же параметрами слоев, что и на рис. 3, но при наличии отклонения ориентаций оптических осей слоев. На пересечении бриллюэновских ЗЗ возникает вырожденная ЗЗ. Ее можно идентифицировать по равенству действительных и мнимых частей блоховских волновых чисел, а также по тому, что действительная часть волнового числа лежит внутри зоны Бриллюэна. Черные линии – те же, что на рис. 3. – приведены для сравнения.

 

Итак, факт, что на частотах ЗЗ действительная часть блоховского волнового числа не лежит на границе зоны Бриллюэна, может служить индикатором наличия вырожденной ЗЗ.

Следует отметить, что условия формирования вырожденной ЗЗ внутри бриллюэновской ЗЗ более сложные, чем условия формирования вырожденной ЗЗ вдали от бриллюэновских ЗЗ. Помимо пересечения дисперсионных ветвей требуются дополнительные условия на параметры слоев ФК. Для иллюстрации рассмотрим ФК с периодом из двух слоев одинаковой толщины . Параметры первого слоя: обыкновенная диэлектрическая проницаемость , необыкновенная - . Параметры второго слоя: обыкновенная диэлектрическая проницаемость , необыкновенная - .

Нетрудно видеть, что в случае параллельных оптических осей дисперсионные зависимости такого ФК совпадают с изображенными на рис. 3. Однако если отклонить оптические оси слоев на некоторый угол (в плоскости слоев), то, несмотря на гибридизацию обыкновенной и необыкновенной волн, вырожденная ЗЗ не возникнет. Это показано на рис. 5 для случая отклонения оптических осей на угол 0,3 рад.

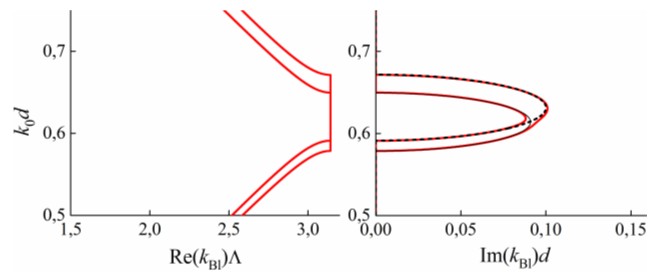
Рис. 5. Дисперсионные кривые (красные) блоховских волн в анизотропном ФК при наличии отклонения оптических осей слоев (в плоскости слоев). На пересечении бриллюэновских ЗЗ не возникает вырожденная ЗЗ. Параметры ФК приведены в тексте. Данный рисунок показывает, что пересечения действительных и мнимых компонент дисперсионных ветвей разных блоховских волн на частотах бриллюэновских ЗЗ не достаточно для формирования вырожденной ЗЗ. Черные линии – те же, что на рис. 3. – приведены для сравнения.

 

Формирование вырожденной границы ЗЗ. Результаты численных расчетов.

         Вернемся к вопросу о формировании вырожденной границы. В данном разделе приведем результаты численных расчетов дисперсионных ветвей ФК, иллюстрирующие механизм формирования вырожденной границы ЗЗ. На рис. 6 представлена зависимость  в сверхрасширенной дисперсионной картине. На этом графике есть три области обозначенные 1, 2 и 3 (пунктирные линии). Это области частот, в которых  то есть это запрещенные зоны. Используя , мы можем классифицировать ЗЗ 1 и 3 как бриллюэновские ЗЗ, а ЗЗ 2 – как вырожденную ЗЗ.

 

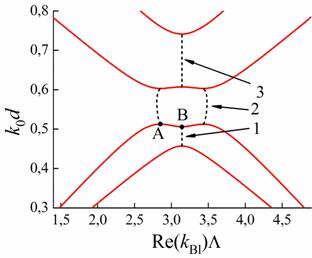
Рис. 6. Сверхрасширенная картина дисперсионной зависимости  частоты  от  ( - толщины слоев,  - период ФК). Точки сплошных линий отвечают бегущим волнам, точки пунктирных линий принадлежат ЗЗ. 1 и 3 – бриллюэновские ЗЗ, 2 – вырожденная ЗЗ. А – граница вырожденной ЗЗ, B – граница бриллюэновской ЗЗ.

 

Нижний край вырожденной запрещенной зоны обозначен точкой A, верхний край ближайшей бриллюэновской запрещенной зоны обозначен точкой B. Вблизи точки B зависимость  (описывающую бегущие волны) можно разложить

                                                            (2)

при этом оказывается, что . Действительно, несложно заметить, что дисперсионная кривая является вогнутой в точке B. При плавном изменении параметров системы положение точек A и B плавным образом меняется. При этом точка A может плавно двигаться вдоль сплошной кривой налево и направо и даже (пройдя через точку B) может подняться вдоль бриллюэновской границы  (см. Рис.7).

 

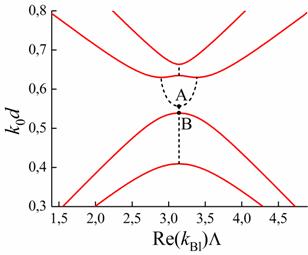
Рис. 7.

 

Если в этом случае около точки B разложить зависимость  так же, как в (2), то оказывается, что .

         Поскольку B есть не что иное как обыкновенная граница бриллюэновской ЗЗ, то в обоих случаях . Однако, пока точка A лежит на дисперсионной кривой левее точки B . А когда точка A лежит на границе зоны Бриллюэна выше точки B . При этом из положения на рис. 6 в положение на рис. 7 система переходит путем непрерывных преобразований своих параметров, то есть точка A, непрерывно двигаясь вверх вдоль дисперсионной кривой, доходит до точки B и затем поднимается вверх. Т. о. когда точка A проходит через точку B, параметр разложения  меняет знак. Следовательно, в момент, когда точки А и Bсовпадают (см. Рис. 8)  и разложение в точке B принимает вид

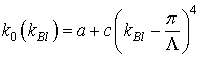                                                                                 (3)

Рис. 8.

 

Численные расчеты подтверждают эти рассуждения. На рисунке 9 приведены результаты численных расчетов зависимости коэффициента  в разложении (2) от расстояния  (по частоте в единицах ) между точками A и B. Расчеты проводились для ФК с периодом из двух слоев одноосного немагнитного материала одинаковой толщины . Оптические оси слоев лежат в плоскости слоев. Угол между оптическими осями слоев – 0,5 рад. Обыкновенные диэлектрические проницаемости первого и второго слоев равны, соответственно,  и , необыкновенные менялись от 6,2 до 6,53 для первого слоя и от 5,7 до 6,03 для второго слоя. Как видно из рисунка 9, при стремлении расстояния  между точками A и B к нулю стремится к нулю и коэффициент  в разложении (2).

 

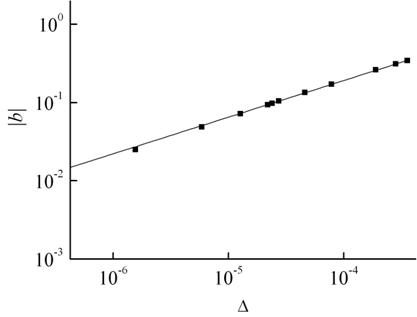
Рис. 9. Зависимость коэффициента  в разложении (2) от расстояния (по частоте)  между границами A и B вырожденной и бриллюэновской ЗЗ. Параметры ФК приведены в тексте. Квадраты – результаты численных расчетов, прямая – линия тренда, проведенная через квадраты.

 

Заметим, что, хотя все предыдущие рассуждения приводились на примере анизотропных ФК, она также справедливы и для магнитофотонных кристаллов с со слоями из анизотропных материалов, с параллельными оптическими осями слоев.

Таким образом, исходя из приведенных качественных рассуждений и результатов численных расчетов, вырожденная граница запрещенной зоны возникает тогда, когда происходит касание границы бриллюэновской запрещенной зоны и границы вырожденной запрещенной зоны.

 

Заключение.

Для случая одномерного ФК нами рассмотрены условия формирования вырожденной границы запрещенной зоны, т.е. такой границы  ЗЗ, в окрестности которой дисперсионная зависимость описывается параболой 4-й степени . Вырожденная граница запрещенной зоны интересна тем, что на частотах в ее окрестности спектр ФК имеет решение в виде замороженной моды. В данной работе показано, что вырожденная граница запрещенной зоны формируется тогда, когда в ФК некоторая частота (которая и будет частотой  вырожденной границы ЗЗ) является одновременно границей бриллюэновской и вырожденной запрещенных зон. Данный вывод справедлив для любого одномерного ФК из анизотропных и гиротропных материалов. При этом вырожденная ЗЗ, участвующая в формировании вырожденной границы ЗЗ, может быть образована не только на частотах вдали от бриллюэновских ЗЗ, но и на частотах пересечения двух бриллюэновских ЗЗ, соответствующих разным блоховским модам. Таким образом, обосновано существование ФК, в которых реализуется вырожденная граница ЗЗ и соответствующая замороженная мода, и указаны достаточные условия формирования вырожденной границы.

 

Литература.

1.                 E. Yablonovitch, “Inhibited Spontaneous Emission in Solid-State Physics and Electronics,” Phys. Rev. Lett. 58, 2059-2062 (1987).

2.                 S.G. Johnson, J. D. Joannopoulos. Photonic crystals: the road from theory to practice. Kluwer Academic Publisher, London, 2002.

3.                 M. Inoue and T. Fujii, “A theoretical analysis of magneto-optical Faraday effect of YIG films with random multilayer structures,” J. Appl. Phys. 81, 5659-5661 (1997).

4.                 S. Fan, P. R. Villeneuve, J. D. Joannopoulos, H. A. Haus “Channel Drop Tunneling through Localized States,” Phys. Rev. Lett. 80, 960-963 (1998).

5.                 M.J. Steel, M. Levy, and R.M. Osgood, Jr., “Photonic Bandgaps with Defects and the Enhancement of Faraday Rotation” J. Lightwave Technol. 18, 1297-1309 (2000).

6.                 S. Fan, “Sharp asymmetric line shapes in side-coupled waveguide-cavity systems,” Appl. Phys. Lett. 80, 908-910 (2002).

7.                 A. Figotin and I. Vitebskiy, “Gigantic transmission band-edge resonance in periodic stacks of anisotropic layers,”Phys. Rev. E 72, 036619 (2005).

8.                 A. Figotin and I. Vitebskiy, “Frozen light in photonic crystals with degenerate band edge,” Phys. Rev. E 74, 066613 (2006).

9.                 A. Figotin and I. Vitebskiy, “Electromagnetic unidirectionality in magnetic photonic crystals,” Phys. Rev. B 67, 165210 (2003).

10.             J. Ballato, A. Ballato, A. Figotin and I. Vitebskiy, “Frozen light in periodic stacks of anisotropic layers Frozen light in periodic stacks of anisotropic layers,” Phys. Rev. E 71, 036612 (2005).

11.             A. Figotin and I. Vitebskiy, “Nonreciprocal magnetic photonic crystals,” Phys. Rev. E 63, 066609 (2001).

12.             M. Levy, “Normal modes and birefringent magnetophotonic crystals,” J. Appl. Phys. 99, 073104 (2006).

13.             A.M. Merzlikin, A.P. Vinogradov, M. Inoue, and A.B. Granovsky, “Giant photonic Hall effect in magnetophotonic crystals” Phys. Rev. E 72, 046603 (2005).

14.             Z. Yu., G. Veronis, Z. Wang, and S. Fan, “One-Way Electromagnetic Waveguide Formed at the Interface between a Plasmonic Metal under a Static Magnetic Field and a Photonic Crystal,” Phys. Rev. Lett. 100, 023902 (2008).

15.             F. Wang and A. Lakhtakia, “Intra-Brillouin-zone bandgaps due to periodic misalignment in one-dimensional magnetophotonic crystals,” Appl. Phys. Lett. 92, 011115 (2008).

16.             I. L. Lyubchanskii, N. N. Dadoenkova, M. I. Lyubchanskii, E. A. Shapovalov, A. Lakhtakia, and Th. Rasing, “One-dimensional bigyrotropic magnetic photonic crystals,” Appl. Phys. Lett. 85, 5932-5934 (2004).

17.             F. Wang and A. Lakhtakia “Magnetically controllable intra-Brillouin-zone band gaps in one-dimensional helicoidal magnetophotonic crystals,” Phys. Rev. B 79, 193102 (2009).

18.             M. Inoue, R. Fujikawa, A. Baryshev, A. Khanikaev, P. B. Lim, H. Uchida, O. Aktsipetrov, A. Fedyanin, T. Murzina, and A. Granovsky, “Magnetophotonic crystals,” J. Phys. D 39, R151 (2006).

19.             G. Shabtay, E. Eidinger, Z. Zalevsky, D. Mendlovic, and E. Marom, “Tunable birefringent filters - optimal iterative design,” Opt. Express 10, 1534-1541 (2002).

20.             I. Љolc, “A new kind of double refracting filter,” Czech. J. Phys., Sect. A 4, 65-66 (1954).

21.             P. Yeh, “Electromagnetic  propagation in birefringent  layered media,”  J. Opt. Soc. Am. 69, 742-756 (1979).

22.             R. Zengerle, “Light propagation in singly and doubly periodic planar waveguides,” J. Mod. Opt. 34, 1589-1617 (1987).

23.             E. Cojocaru, “Forbidden Gaps in Periodic Anisotropic Layered Media,” Appl. Opt. 39, 4641-4648 (2000).

24.             A. M. Merzlikin, A. P. Vinogradov, M. Inoue, A. B. Khanikaev, and A. B. Granovsky, “The Faraday effect in two-dimensional magneto-photonic crystals,” J. Magn. Magn. Mater. 300, 108-111 (2006).

25.             A. M. Merzlikin, A. P. Vinogradov, A. V. Dorofeenko, M. Inoue, M. Levy, and A. B. Granovsky, “Controllable Tamm states in magnetophotonic crystal,” Physica B 394, 277-280 (2007).

26.             M. Levy and A. A. Jalali, “Band structure and Bloch states in birefringent one-dimensional magnetophotonic crystals: an analytical approach,” J. Opt. Soc. Am. B 24, 1603-1609 (2007).

27.             A. A. Jalali and M. Levy, “Local normal-mode coupling and energy band splitting in elliptically birefringent one-dimensional magnetophotonic crystals,” J. Opt. Soc. Am. B 25, 119-125 (2008).

28.             A.M. Merzlikin, Miguel Levy, A.A. Jalali, and A.P. Vinogradov “Polarization degeneracy at Bragg reflectance in magnetized photonic crystals,” Phys. Rev. B 79, 195103 (2009).