Исследование дисперсионных характеристик поверхностной волны в однопроводниковой меандровой линии

 

Е. М.  Арсеньева., В. И. Калиничев, В. А. Калошин

Институт радиотехники и электроники им. В.А.Котельникова РАН

Получена 14 января 2011 г.

 

Аннотация. Численно исследованы дисперсионные характеристики проволочной и ленточной меандровых линий. Рассчитаны зависимости частотных характеристик фазового замедления и затухания поверхностной волны от геометрических параметров линии. Показано, что рассмотренные однопроводниковые меандровые линии при относительно малом замедлении обладают малым затуханием в широком диапазоне частот.
Ключевые слова: СВЧ диапазон, волноводы и линии передач, дисперсионные характеристики.

Abstract. Dispersive characteristics conductor and strip meander lines are numerically investigated. Dependences of phase delay and attenuation in some types of surface wave on geometrical parameters of the line are computed. It is shown that the examined single conductor meander lines are capable of guiding the surface wave with small attenuation under relatively small slow coefficients in the wide range of frequencies.

Keywords: Microwave region, Waveguides and lines, Dispersion relations.

 

                                                                                                              

Введение

         Ленточные меандровые линии поверхностной волны были предложены в работе [1] как альтернатива излучающему кабелю для связи в закрытых помещениях и туннелях.

В данной работе на основе метода конечных элементов проводится численное исследование дисперсионных характеристик поверхностной волны в ленточной и проволочной меандровых линиях.

Сначала исследуем дисперсионные характеристики меандровой линии  из круглого металлического провода. Дисперсионные характеристики изогнутого круглого провода будем рассматривать как референсные значения для сравнения с другими типами меандровых линий с аналогичными геометрическими параметрами.

 

Меандровая линия из круглого провода

Модель исследуемой линии показана на рис.1а. Металлический круглый провод диаметром d изогнут в форме сопрягающихся одинаковых полуокружностей радиуса R, образуя меандр с периодом P и шириной W, измеряемой между осями провода в верхней и нижней точках меандра, как показано на рис. 1 а. При этом полная ширина линии с учетом толщины провода равна W+d. В данной геометрии меандра имеет место очевидное соотношение P=4R, W=2R. Предполагаем, что провод расположен в свободном пространстве. Для исследования частотной характеристики замедленной волны в такой линии воспользуемся методом конечных элементов в комбинации с резонаторным методом. В данном методе отрезок линии с целым числом периодов помещается в резонатор достаточно больших поперечных размеров так, чтобы боковые металлические стенки не влияли существенно на фазовую скорость волны в линии (рис.1б).

Рис.1. Модель меандровой линии из круглого металлического провода:

а - основные параметры, б - отрезок линии с 3-мя периодами в резонаторе.

 

Предполагаем, что резонатор настроен на основной резонанс замедленной волны в линии, при котором по длине резонатора укладывается половина длины замедленной волны. Численно определяя  резонансную частоту и добротность этого типа колебаний, можем рассчитать соответствующие этому резонансу замедление волны и ее затухание. В зависимости от длины резонатора и числа периодов линии в нем получаем разные резонансные частоты и добротности, которые пересчитываются в величины замедления и затухания линии на разных частотах. Тем самым получаем дисперсионные характеристики замедленной волны линии в дискретных частотных точках в некотором заданном диапазоне частот.

Рассмотрим вариант линии из медного провода с параметрами d = 0.5 мм, R=2.5 мм, P=10 мм, W= 5 мм.  Для идентификации требуемого типа колебаний в резонаторе надо построить распределение поля  в нем и по этому распределению определить его соответствие поверхностной замедленной волне линии.

В качестве иллюстрации на рис.2 представлены примеры рассчитанных амплитудных распределений электрического поля в резонаторе на резонансной частоте основного типа колебаний 3.855 ГГц для 3-х периодов линии (длина резонатора 30 мм) с указанными выше параметрами. Легко определить, что данной частоте соответствует фазовое замедление волны в линии U=1.30. На рис.2а  показаны распределения  амплитуды электрического поля в плоскости линии (ZOY) и перпендикулярной к ней (XOY), а также на торцевой стенке резонатора (XOZ). Наглядно видно, что поле, в основном, концентрируется вблизи изогнутого металлического провода, что является характерным для поверхностной волны. В дополнение на рис.2б представлены распределения электрического поля вдоль линий, расположенных в центральной поперечной плоскости резонатора Y=15 мм. Красная кривая  показывает распределение поля вдоль линии, лежащей в плоскости меандра и параллельной оси Z, начинаясь на оси меандра и заканчиваясь на верхней стенке резонатора при Z=15 мм.  Синяя кривая  начинается в той же точке на оси меандра и показывает распределение поля в плоскости, перпендикулярной меандру при движении в направлении оси Х, заканчиваясь на боковой стенке резонатора при X=15 мм. Из этих распределений следует, что скорость спадания поля волны почти одинакова при удалении от линии в разных направлениях, начиная с расстояния от оси примерно 5 мм. Представленные спадающие при удалении от оси меандра распределения поля позволяют сделать вывод о том, что данный тип колебаний в резонаторе образован  исследуемой поверхностной волной меандровой линии. Аналогичные распределения могут быть построены и на других частотах для другого числа периодов линии в резонаторе.

 

Рис 2. Распределения амплитуды электрического поля на резонансной частоте основного типа колебаний:

а - в различных плоскостях резонатора (логарифмический масштаб шкалы),

б - вдоль двух линий в центральной поперечной плоскости резонатора (красный – в плоскости меандра, синий – перпендикулярно плоскости меандра).

 

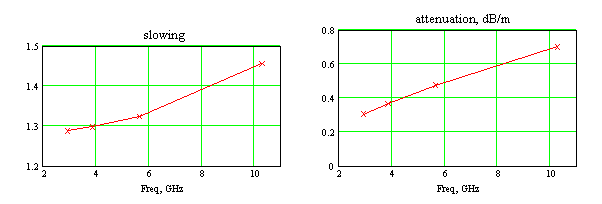
         На рис.3 представлены рассчитанные с помощью описанного резонаторного метода частотные зависимости фазового замедления и погонного затухания меандровой линии в нескольких частотных точках, соответствующих числу периодов от 1 до 4. Как и следовало ожидать, с ростом частоты замедление и  затухание в линии возрастают. Однако в данной линии из круглого провода затухание остается сравнительно малым, менее 0.7 дБ/м, до частоты 10 ГГц.

а                                                                        б

Рис.3. Дисперсионные характеристики меандровой линии из круглого металлического провода:

а - фазовое замедление, б – затухание.

 

Ленточная меандровая линия

Ленточная меандровая линия (ЛМЛ) представляет собой изогнутую металлическую полоску (ленту), плоскость которой совпадает с плоскостью меандра (см. рис.4). На рис. 4а изображена меандровая линия с плавными изгибами, а на рис. 4б – прямоугольный меандр.

 

а                                                       б

Рис. 4. Ленточные меандровые линии

а – плавно изогнутый меандр, б – прямоугольный меандр.

 

Предварительно исследуем ЛМЛ c шириной ленты w, профиль которой представляет сопряжение двух одинаковых полуокружностей с радиусом R, так что P=4R, W=2R (рис.5а).  В данном случае полная ширина меандровой линии W+w. Для нее можем применить тот же метод исследования дисперсионных характеристик, что и для меандра из металлического провода, помещая отрезок линии с целым числом периодов в резонатор и рассчитывая его резонансную частоту и добротность на основном типе колебаний (рис.5б).

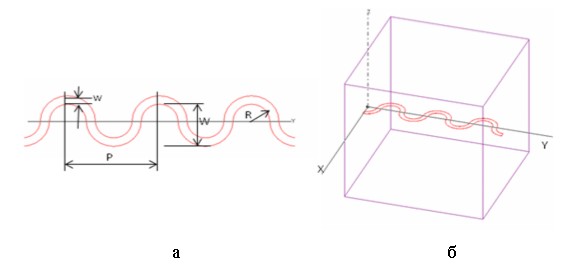
Рис.5. Модель меандровой линии из металлической ленты с криволинейным профилем:

а - основные параметры, б - отрезок линии в резонаторе.

 

Рассмотрим вариант линии из тонкой медной ленты с толщиной 0.018 мм с параметрами  w= 1 мм, R=2.5 мм, P=10 мм, W= 5 мм.  Распределения поля поверхностной замедленной волны  в разных плоскостях резонатора на резонансной частоте 3.880 ГГц (соответствующее фазовое замедление U=1.29) показаны на рис. 6 а. Эти распределения  аналогичны представленным выше на рис. 2 а с учетом того, что плоскости линий повернуты на 90⁰ относительно друг друга.

 

Рис.6. Распределения амплитуды электрического поля на резонансной частоте основного типа колебаний:

а - в различных плоскостях резонатора (логарифмический масштаб шкалы),

б - вдоль двух линий в центральной поперечной плоскости резонатора (красный – в плоскости меандра, синий – перпендикулярно плоскости меандра).

 

Распределения на рис.6б построены вдоль линий, расположенных в центральной поперечной плоскости резонатора Y =15 мм. Синяя кривая начинается на оси меандра и показывает распределение поля в перпендикулярном направлении вдоль оси Z, заканчиваясь на верхней стенке резонатора при Z=15 мм. Красная кривая  начинается в той же точке на оси меандра и показывает распределение в плоскости меандра при движении в направлении оси Х (так что металлическая лента не пересекается), заканчиваясь на боковой стенке резонатора при X=15 мм. Из этих распределений следует, что, как и в случае меандра из круглого провода, скорость спадания поля волны почти одинакова при удалении от линии в разных направлениях, начиная с расстояния от оси примерно 5 мм.

На рис.7 представлены рассчитанные с помощью резонаторного метода зависимости фазового замедления и погонного затухания от частоты, в нескольких частотных точках, соответствующих числу периодов от 1 до 5. Пунктирной линией на тех же графиках показаны соответствующие характеристики для рассмотренного выше меандра из медного провода диаметром 0.5 мм. В сравнении с круглым проводом замедление волны в линии из металлической ленты почти такое же, а затухание выше, достигая величины 0.9 дБ/м на частоте 10 ГГц. Повышенное затухание в ленточной линии  объясняется возрастанием плотности тока на краях ленты.
       

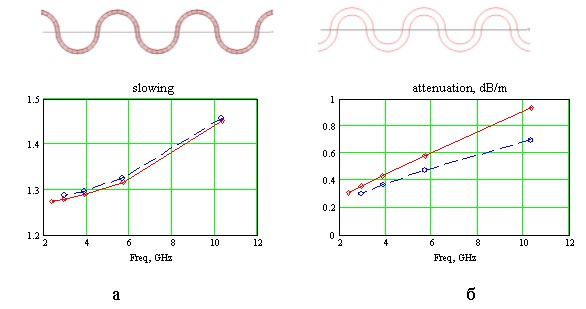
Рис.7. Дисперсионные характеристики меандровой линии из металлической ленты с криволинейным профилем (красный цвет) и периодически изогнутой меандровой линии из круглого провода (синий цвет):

а - фазовое замедление, б – затухание.

 

Ленточная меандровая линия с прямоугольным профилем

Вероятно, наиболее простой и интересной с точки зрения практического использования является ленточная меандровая линия с прямоугольным профилем с периодом P и шириной W, образованная тонкой металлической полоской шириной  w (рис.8а). Полная ширина линии равна W+w. Как и в предыдущих случаях, наиболее эффективным методом ее численного исследования является резонаторный метод, в котором отрезок линии с целым числом периодов помещается в резонатор (рис.8б), для которого рассчитывается резонансная частота и добротность основного типа колебаний.

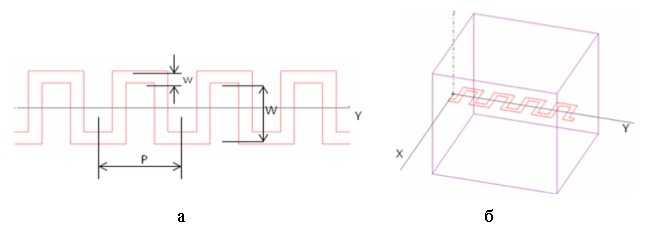
Рис.8. Модель меандровой линии с прямоугольным профилем:

а - основные параметры, б - отрезок линии с 4-мя периодами в резонаторе.

 

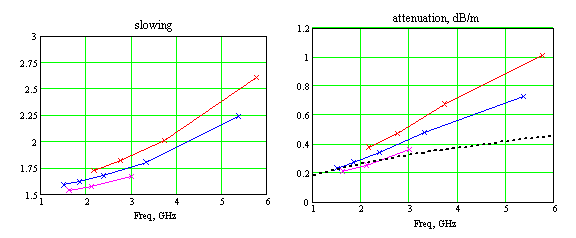
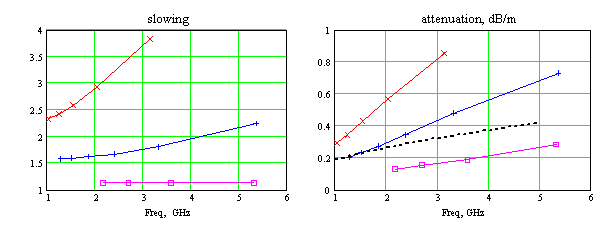
Рассмотрим вариант линии с периодом, равным 1/8 длины волны на частоте 3 ГГц (P=12.5 мм), и с шириной ленты w=2 мм.  Толщина ленты t=0.018 мм, материал - медь. Сначала будем исследовать зависимость дисперсионных характеристик от ширины W. На рис. 9 а, б представлены рассчитанные зависимости замедления и затухания в линии от частоты, при трех значениях ширины W=20 мм, 10 мм и 3 мм. Видим, что с увеличением ширины меандра замедление возрастает, как и следовало ожидать из простых геометрических представлений об увеличении длины меандра с увеличением его ширины.

а                                                                         б

Рис. 9. Дисперсионные характеристики линии для разной ширины меандра при заданном периоде P=12.5 мм и ширине полоски w=2 мм:

а – фазовое замедление, б - затухание

красный - W=20 мм,  синий - W=10 мм,  пурпур - W=3 мм.  

 

Одновременно с ростом замедления происходит рост затухания. Для сравнения  с другими полосковыми линиями передачи пунктирная линия черного цвета на рис.9б и ниже на рис.11б и рис.12б обозначает затухание 50-ом симметричной полосковой линии с воздушным заполнением с расстоянием между экранами 3.2 мм и шириной линии 4.6 мм, рассчитанное по приближенным аналитическим формулам [2]. Из рис.9б следует, что при ширине меандра 20 мм затухание в нем больше, чем в полосковой линии во всем исследованном диапазоне частот; при ширине меандра 10 мм затухание в нем соизмеримо с затуханием полосковой линии на частотах до 2 ГГц и становится выше на более высоких частотах; при ширине меандра 3 мм затухание в нем меньше затухания полосковой линии во всем исследованном диапазоне.

Таким образом, относительно зависимости дисперсионных характеристик ленточной меандровой линии от ее ширины  можем сделать вывод о том, что использование как узких, так и широких линий нецелесообразно в силу малого замедления в первом случае и большого затухания во втором. Поэтому для практики наиболее подходящим вариантом из рассмотренных представляется меандр с шириной, примерно равной периоду, в данном случае W=10 мм (при этом полная ширина линии W+w=12 мм). В соответствии с рис.9 для такой линии на частоте 3 ГГц при замедлении около 1.8  затухание не превосходит 0.5 дБ/м, хотя при этом оно немного выше затухания симметричной полосковой линии.

На рис.10а показаны распределения электрического поля замедленной волны в различных плоскостях в резонаторе на частоте основного типа колебаний 1.854 ГГц, соответствующей длине резонатора 50 мм и четырем периодам отрезка линии в нем. Замедление волны на этой частоте примерно 1.6, а затухание 0.28 дБ/м. Как и следовало ожидать, поле, в основном, сосредоточено в окрестности металлической полоски, что характерно для поверхностной замедленной волны.

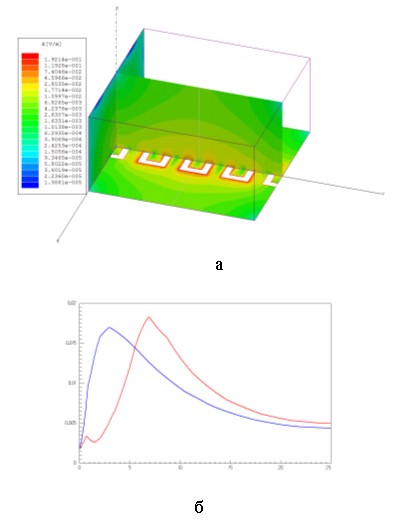
Рис.10. Распределения амплитуды электрического поля на резонансной частоте основного типа колебаний:

а - в различных плоскостях резонатора (логарифмический масштаб шкалы),

б - вдоль двух линий в центральной поперечной плоскости резонатора

 (красный – в плоскости меандра, синий – перпендикулярно плоскости меандра).

 

На рис.10б показаны зависимости амплитуды электрического поля от расстояния до оси меандра в двух ортогональных плоскостях: в плоскости меандра и перпендикулярно к ней. Распределения построены вдоль линий, расположенных в центральной поперечной плоскости резонатора Y =25 мм. Синяя кривая начинается на оси меандра, показывает распределение поля в перпендикулярном направлении вдоль оси Z и заканчивается на верхней стенке резонатора при Z=25 мм. Красная кривая  начинается в той же точке на оси, показывает распределение в плоскости меандра при движении в отрицательном направлении оси Х (так что металлическая лента не пересекается) и заканчивается на боковой стенке резонатора при X=-25 мм. На расстоянии, превышающем 15 мм от оси линии, скорость спадания поля вдоль обоих направлений становится примерно одинаковой.

    Исследуем зависимость дисперсионных характеристик меандровой линии от ее периода при фиксированных других параметрах. На рис. 11 представлены характеристики при ширине меандра W=10 мм, ширине полоски w=2 мм и при трех разных значениях периода: P= 10 мм, 12.5 мм и 15 мм. Видно, что с увеличением периода линии замедление и затухание в ней уменьшаются. Для периода P=15 мм потери в меандре немного меньше потерь в симметричной полосковой линии до частоты 2.5 ГГц и начинают возрастать по сравнению  с потерями в ней на частотах выше 2.5 ГГц.

               а                                                                         б

Рис. 11. Дисперсионные характеристики линии для разных периодов меандра при заданной ширине W=10 мм и ширине полоски w=2 мм:

а – фазовое замедление, б - затухание

красный - P=10 мм,  синий - P=12.5 мм,  пурпур - P=15 мм . 

 

Ширина металлической ленты, образующей меандр, представляет еще один параметр, влияющий на его дисперсионные характеристики. На рис.12  представлено сравнение частотных зависимостей замедления и затухания для трех разных значений ширины w=1 мм, 2 мм и 3 мм для периода P =12.5 мм и ширины меандра W =10 мм.

 

 

Рис. 12. Дисперсионные характеристики линии для разных ширин полоски, образующей меандр, при P=12.5 мм и W=10 мм:

а – фазовое замедление, б - затухание

1 - w=1 мм,  2 - w=2 мм,  3 - w=3 мм.   

С увеличением ширины полоски меандра потери в линии уменьшаются и при ширине полоски 3 мм становятся немного меньше потерь в полосковой линии на частотах до 2.5 ГГц. Следует отметить, что при заданных параметрах меандровой линии частотная зависимость потерь в ней более сильная, чем в симметричной полосковой линии.

В заключение этого раздела сравним дисперсионные характеристики для полосковых меандровых линий  с криволинейным и прямоугольным профилями. На рис.представлены характеристики линий с аналогичными геометрическими параметрами:

                

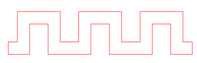
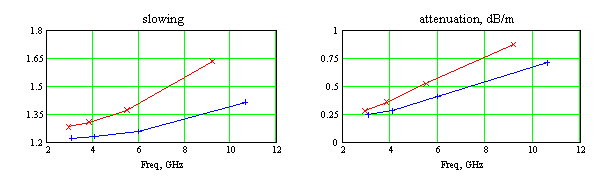
а                                                                        б

Рис. 13. Сравнение ленточных меандровых линий с криволинейным (синий) и прямоугольным (красный) профилями. Параметры линий:  P=10 мм, W=5 mm, w=2 mm:

а - фазовое замедление, б – затухание.

 

периодом, шириной линии и шириной полоски. Материал обеих линий – медь толщиной 0.018 мм. Видно, что при заданных одинаковых параметрах замедление и затухание волны в прямоугольном меандре выше, чем в меандре с плавно изогнутым профилем.

 

Заключение

В результате проведенных исследований рассчитаны дисперсионные характеристики фазового замедления и затухания поверхностной волны для некоторых типов меандровых линий. Сранение показывает, что меандр из круглого металлического провода обладает наименьшим погонным затуханием при одинаковом замедлении в сравнении с полосковыми меандровыми линиями, вследствие разного распределения плотности тока на круглом проводе и металлической полоске. Линии с прямоугольным профилем меандра имеют замедление и затухание, которые могут изменяться в широких пределах в зависимости от соотношения периода и ширины линии. В конкретных приложениях эти параметры должны выбираться в зависимости от заданных показателей качества.

Работа выполнена при поддержке РФФИ, проект №10-07-00709-а.

 

Список литературы

1. Е. М. Арсеньева, В. И. Калиничев, В. А. Калошин. Новые типы линий для радиосвязи в УКВ и СВЧ диапазонах. Труды 3-й Всероссийской конференции «Радиолокация и радиосвязь», Москва, 2009 (http://jre.cplire.ru/jre/library/3conference/pdffiles/pd007.pdf).

2. D. Pozar.  Microwave Engineering, Addison-Wesley, Amherst, 1990, pp.178-180.