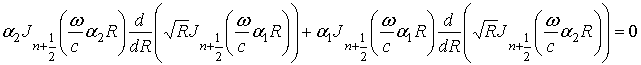УДК 517.958; 621.372.8
ИССЛЕДОВАНИЕ КИРАЛЬНЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ СИСТЕМ
А.
Н. Боголюбов, Ю. В. Мухартова, Гао Цзесин
физический
факультет МГУ имени М.В. Ломоносова, кафедра математики
Получена 27 января 2011 г.
Аннотация. В работе рассмотрены две задачи: спектральная задача в области с киральным заполнением и начально-краевая задача о возбуждении электромагнитных колебаний в области с неоднородным киральным заполнением. Получено характеристическое уравнение для собственных частот сферического кирального резонатора и вид собственных полей. Для начально-краевой задачи предложена обобщенная постановка, которая в дальнейшем может быть использована для численного решения задач рассматриваемого типа. Доказано существование и единственность обобщенного решения.
Ключевые слова: киральные среды, сферический резонатор, собственные частоты, задача возбуждения.
Abstract. In this paper two problems are considered. The first one is a spectral problem for the area with uniform chiral filling. The second one is the initial-boundary problem of excitation of oscillations in a region with a nonhomogeneous chiral filling. The dispersive equation and the eigenfields are obtained for a spherical chiroresonator. For the initial-boundary problem a generalized formulation, that can be further utilized for the numerical solution, is proposed. The existence and uniqueness of a generalized solution is proved.
Key words: chiral media, spherical resonator, eigenvalues, initial-boundary problem.
Введение.
В настоящее время в радиофизике все больший интерес вызывает применение метаматериалов, с использованием которых возможно создание систем и устройств с уникальными свойствами. В частности, большой интерес вызывает создание систем, использующие свойства бианизотропных и киральных сред. Теоретическое исследование таких систем методами математической физики представляет весьма важную и интересную задачу. Можно выделить два класса подобных задач: спектральные задачи, заключающиеся в исследовании резонаторных систем с киральным заполнением, и начально-краевые задачи возбуждения, в которых исследуются процессы возбуждения различных волноведущих систем с киральным заполнением и процессы распространения электромагнитных волн в подобных системах.
Естественные киральные
среды были известны с начала 19 века. Термин "киральный" введен
Уильямом Томсоном и означает свойство объекта не совмещаться со своим зеркальным
отображением (в плоском зеркале) ни при каких перемещениях и вращениях. Естественными
киральными объектами являются молекулы сахаров, аминокислот, ДНК и органических
полимеров. К числу искусственных киральных объектов можно отнести спирали, лист
Мебиуса, неправильный тетраэдр и т.д. [11] – [3]. Известно [4], что в случае
киральной среды, изготовленной при помощи произвольным образом ориентированных
и равномерно распределенных в некиральном веществе проволочных пружинок,
потерями в которых можно пренебречь, материальные уравнения для гармонических
по времени полей (![]() )
имеют вид
)
имеют вид
![]() ,
,
![]() ,
,
где ![]() ,
, ![]() ,
, ![]() – действительные постоянные,
представляющие собой диэлектрическую проницаемость, магнитную проницаемость и
киральный адмитанс (параметр киральности) среды соответственно. Более того, как
было показано в работе [5], эти материальные уравнения остаются справедливыми
для любой киральной среды без потерь, построенной из киральных объектов
произвольной формы.
– действительные постоянные,
представляющие собой диэлектрическую проницаемость, магнитную проницаемость и
киральный адмитанс (параметр киральности) среды соответственно. Более того, как
было показано в работе [5], эти материальные уравнения остаются справедливыми
для любой киральной среды без потерь, построенной из киральных объектов
произвольной формы.
Первая задача, рассмотренная в данной работе, посвящена исследованию электромагнитных экранированных резонаторов, заполненных однородным киральным веществом. Сферические и цилиндрические резонаторы находят широкое применение в различных областях науки и техники [6]-[8]. Отметим, что математическое решение задачи для сферических резонаторов, заполненных обычной некиральной средой, было получено достаточно давно [9]-[11]. Поскольку в последние годы наблюдается особое внимание к искусственным киральным средам микроволнового диапазона, в которых киральность уже не является малой поправкой, то в связи с этим представляется интересным обобщить эти решения на случай кирального резонатора. В работе предложен алгоритм расчета таких систем. В качестве примера исследован сферический киральный резонатор, для которого получено характеристическое уравнение и вид собственных полей. Показано, что в таком резонаторе могут формироваться только гибридные собственные колебания, чистые E- и H- колебания не возбуждаются.
Вторая задача, рассмотренная в работе, заключается в исследовании процесса возбуждении электромагнитных колебаний заданным распределением зарядов и токов в области с неоднородным киральным заполнением. Область, в которой рассматривается задача, может быть либо конечной с идеально проводящей ограничивающей поверхностью, либо представлять собой дополнение к идеально проводящему ограниченному телу. Вводится специальное функциональное пространство, в котором формулируется обобщенная постановка исследуемой начально-краевой задачи. На основе метода Галёркина доказано существование и единственность слабого решения данной задачи.
Спектральная задача: ограниченная область с киральным заполнением.
Рассмотрим систему уравнений Максвелла в однородной киральной среде, которая характеризуется материальными уравнениями
где ![]() ,
, ![]() , и
, и ![]() – константы. С учетом материальных
уравнений для полей E и H получаем систему
– константы. С учетом материальных
уравнений для полей E и H получаем систему
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
На границе раздела двух
киральных сред с параметрами ![]() ,
, ![]() ,
, ![]() и
и ![]() ,
, ![]() ,
, ![]() соответственно выполняются соотношения
соответственно выполняются соотношения
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]()
![]() ,
,
где n - единичный вектор нормали к поверхности,
направленный из второй среды в первую, ![]() – плотность поверхностного тока, и
– плотность поверхностного тока, и ![]() – плотность поверхностного
заряда.
– плотность поверхностного
заряда.
Если вторая среда является идеальным проводником и поле внутри нее равно нулю, на границе выполняются условия идеально проводящей стенки:
![]() ,
,
![]() ,
,
![]() , (2)
, (2)
где ![]() – плотность наведенного поверхностного
тока, и
– плотность наведенного поверхностного
тока, и ![]() –
плотность наведенного поверхностного заряда.
–
плотность наведенного поверхностного заряда.
Рассмотрим теперь
достаточно общую спектральную задачу. Предположим, что некоторая область V
с граничной идеально проводящей поверхностью ![]() заполнена однородным киральным веществом,
которое описывается уравнениями (1). Для гармонически зависящих от времени
полей
заполнена однородным киральным веществом,
которое описывается уравнениями (1). Для гармонически зависящих от времени
полей ![]() получаем
краевую задачу
получаем
краевую задачу
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
В отличие от случая обычной некиральной среды, полученные уравнения оказываются связанными. Тем не менее, можно ввести такие линейные комбинации векторов Е и Н
![]() ,
,
![]() ,
,
что уравнения для функций u и v окажутся несвязанными:
Определённая сложность
решения рассматриваемой спектральной задачи связана с тем, что для векторов u и v нельзя получить на границе ![]() условия, не содержащие
наведенных токов и зарядов, так как они оба содержат в качестве слагаемого
вектор магнитного поля H.
Тем не менее, можно предложить следующий алгоритм исследования собственных
частот и собственных колебаний кирального резонатора. Сначала строится общее
решение системы однородных уравнений (3-6). Далее векторы E и H нужно выразить через найденные векторы u и v и подставить их в однородные граничные условия. Это
позволит получить характеристическое уравнение для нахождения собственных
частот
условия, не содержащие
наведенных токов и зарядов, так как они оба содержат в качестве слагаемого
вектор магнитного поля H.
Тем не менее, можно предложить следующий алгоритм исследования собственных
частот и собственных колебаний кирального резонатора. Сначала строится общее
решение системы однородных уравнений (3-6). Далее векторы E и H нужно выразить через найденные векторы u и v и подставить их в однородные граничные условия. Это
позволит получить характеристическое уравнение для нахождения собственных
частот ![]() .
.
Спектральная задача: сферический киральный резонатор.
В данном разделе предложенная методика применяется для исследования сферического резонатора с киральным заполнением. Пусть область V представляет собой шар радиуса R с идеально проводящей границей. Находим решение u, v системы однородных уравнений (3-6), записанных в сферических координатах. Обозначим через e и h комплексные амплитуды полей E и H. Нетрудно убедиться, что с векторами векторы e и h связаны u и v следующим образом
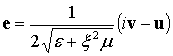

В результате получаем общее решение вида


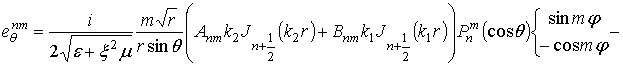
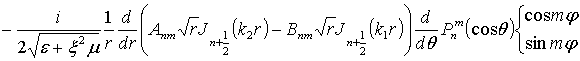
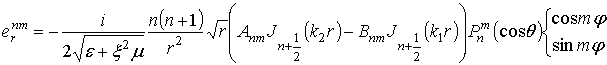
и
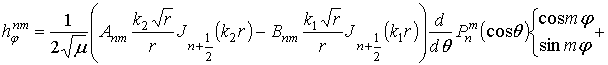
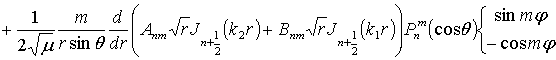
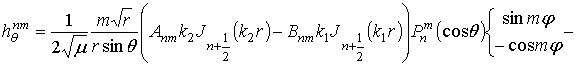
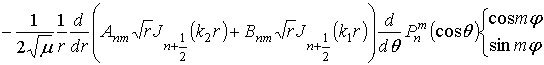
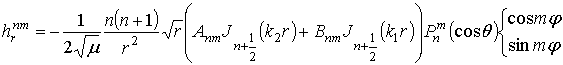
В этих выражениях введены обозначения
![]() и
и ![]() .
.
Поскольку поверхность
шара является идеальным проводником, то для вектора e должно выполняться граничное условие равенства нулю
тангенциальной составляющей ![]() . Потребуем, чтобы компонента
. Потребуем, чтобы компонента ![]() обращалась в нуль при
обращалась в нуль при ![]() . Для этого должна быть
справедлива следующая однородная система уравнений
. Для этого должна быть
справедлива следующая однородная система уравнений
Но если система уравнений (7)
справедлива, то компонента ![]() также обращается в нуль при
также обращается в нуль при ![]() . Отметим, что при этом автоматически
выполняется условие (2) на нормальные составляющие векторов e и h.
. Отметим, что при этом автоматически
выполняется условие (2) на нормальные составляющие векторов e и h.
Однородная система (7)
имеет нетривиальное решение только в том случае, когда ее определитель равен
нулю. Отсюда получается характеристическое уравнение для нахождения собственных
частот ![]() сферического
кирального резонатора:
сферического
кирального резонатора:
(8)
где ![]() и
и ![]() .
.
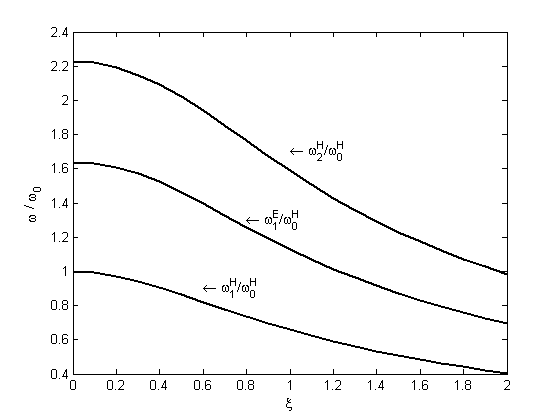
Рис. 1. Зависимость собственных
частот от кирального адмитанса ![]() для
для ![]() . На графике приведены отношения частот к
значению
. На графике приведены отношения частот к
значению ![]() –
наименьшей собственной частоте резонатора при отсутствии киральности (
–
наименьшей собственной частоте резонатора при отсутствии киральности (![]() ). Индексы E и H у частот означают, что в пределе при
). Индексы E и H у частот означают, что в пределе при ![]() они стремятся к собственным
частотам E- и H-колебаний соответственно.
они стремятся к собственным
частотам E- и H-колебаний соответственно.
На рисунке 1 приведены результаты
численного решения уравнения (8), из которых следует, что с ростом параметра ![]() значения собственных
частот уменьшаются и происходит их сближение.
значения собственных
частот уменьшаются и происходит их сближение.
Заметим, что в случае обычной
среды, когда ![]() ,
характеристическое уравнение (8) вырождается в два уравнения
,
характеристическое уравнение (8) вырождается в два уравнения
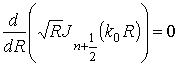 (9)
(9)
и
![]() ,
(10)
,
(10)
где ![]() , так как при этом
, так как при этом ![]() . Уравнения (9) и (10) – это
характеристические уравнения для собственных частот E- и H-колебаний
обычного сферического экранированного резонатора с идеально проводящей границей
соответственно.
. Уравнения (9) и (10) – это
характеристические уравнения для собственных частот E- и H-колебаний
обычного сферического экранированного резонатора с идеально проводящей границей
соответственно.
На основании
подготовительной теоремы Вейерштрасса (см., например, [12]) можно показать, что
решения уравнения (8) непрерывно зависят от параметра киральности ![]() . Обозначим через
. Обозначим через ![]() те из них, которые при
равном нулю параметре киральности совпадают с частотами E-колебаний обычного сферического
резонатора. Воспользуемся первым уравнением системы (7) для того, чтобы найти
связь между коэффициентами
те из них, которые при
равном нулю параметре киральности совпадают с частотами E-колебаний обычного сферического
резонатора. Воспользуемся первым уравнением системы (7) для того, чтобы найти
связь между коэффициентами ![]() и
и ![]() . В результате получим выражения для
комплексных амплитуд собственных колебаний кирального резонатора
. В результате получим выражения для
комплексных амплитуд собственных колебаний кирального резонатора
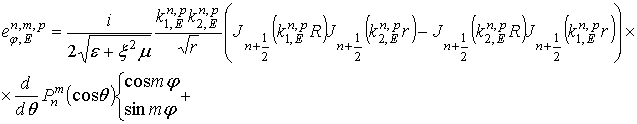
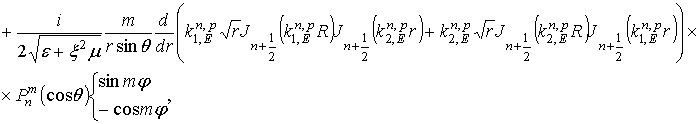
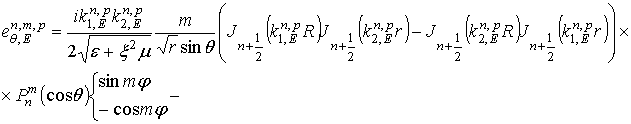
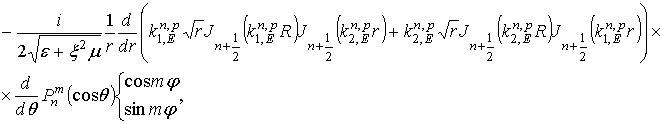
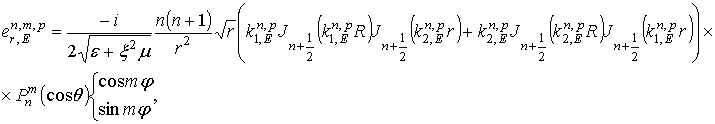
и
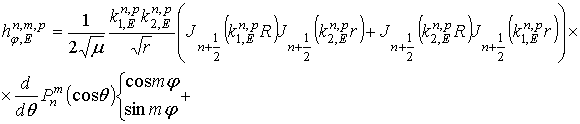

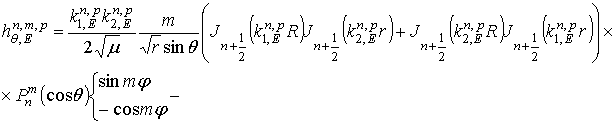

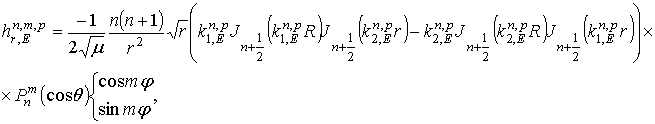
которые в пределе при ![]() с точностью до
множителя
с точностью до
множителя ![]() совпадут
с E-колебаниями обычного сферического
резонатора.
совпадут
с E-колебаниями обычного сферического
резонатора.
Обозначим как ![]() решения характеристического
уравнения (8), совпадающие при равном нулю параметре киральности
решения характеристического
уравнения (8), совпадающие при равном нулю параметре киральности ![]() с собственными
частотами, отвечающими H-колебаниям
обычного некирального резонатора. Найдем связь между коэффициентами
с собственными
частотами, отвечающими H-колебаниям
обычного некирального резонатора. Найдем связь между коэффициентами ![]() и
и ![]() с помощью второго уравнения
системы (7). В результате получим еще одну серию решений для кирального
сферического резонатора
с помощью второго уравнения
системы (7). В результате получим еще одну серию решений для кирального
сферического резонатора


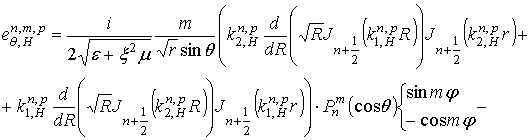
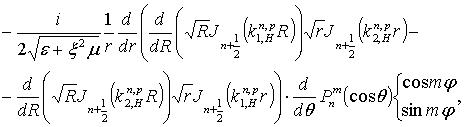
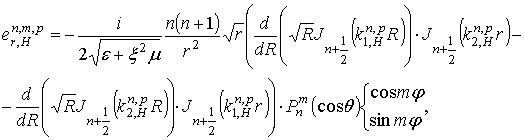
и
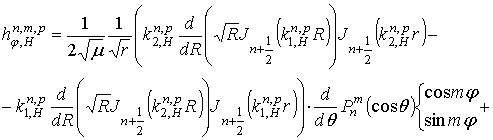
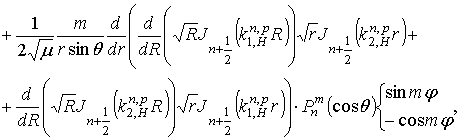

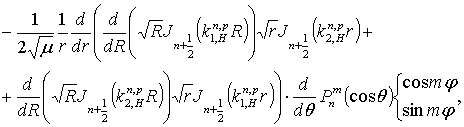

которые в пределе при равном нулю
параметре киральности ![]() с
точностью до множителя
с
точностью до множителя  совпадают с H-колебаниями обычного сферического некирального резонатора.
Следовательно, можно сделать вывод о том, что в киральном резонаторе
поддерживаются только гибридные собственные колебания.
совпадают с H-колебаниями обычного сферического некирального резонатора.
Следовательно, можно сделать вывод о том, что в киральном резонаторе
поддерживаются только гибридные собственные колебания.
Начально-краевая задача: возбуждение электромагнитных колебаний в области с киральным заполнением.
Пусть ![]() – конечное или бесконечное
множество в
– конечное или бесконечное
множество в ![]() .
Если множество конечное, то будем считать, что оно ограничено идеально
проводящей поверхностью
.
Если множество конечное, то будем считать, что оно ограничено идеально
проводящей поверхностью ![]() . Если же множество
. Если же множество ![]() бесконечное, то будем считать,
что
бесконечное, то будем считать,
что ![]() –
дополнение к области
–
дополнение к области ![]() ,
конечно, ограничено поверхностью
,
конечно, ограничено поверхностью ![]() и представляет собой идеальный проводник.
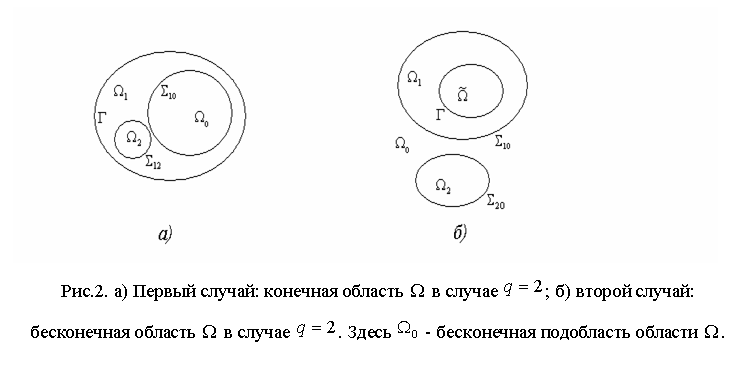
Пусть область
и представляет собой идеальный проводник.
Пусть область ![]() состоит
из конечного числа подобластей:
состоит
из конечного числа подобластей:
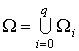
причём все из них, кроме может,
подобласти ![]() ,
конечны, и общая для подобластей
,
конечны, и общая для подобластей ![]() и
и ![]() граница
граница ![]() регулярна и ограниченна. В случае
бесконечной области
регулярна и ограниченна. В случае
бесконечной области ![]() подобласть
подобласть
![]() неограниченна.
Пусть подобласти
неограниченна.
Пусть подобласти ![]() имеют
однородные киральные заполнения с параметрами
имеют
однородные киральные заполнения с параметрами ![]() ,
, ![]() , причём
, причём ![]() и
и ![]() , если подобласть
, если подобласть ![]() неограниченна. В этом случае проводник
неограниченна. В этом случае проводник
![]() и
ограниченные киральные вставки
и
ограниченные киральные вставки ![]() помещены в обычную непроводящую среду,
характеризующуюся диэлектрической проницаемостью
помещены в обычную непроводящую среду,
характеризующуюся диэлектрической проницаемостью ![]() и магнитной проницаемостью
и магнитной проницаемостью ![]() .
.
Предположим, что в области ![]() имеются сосредоточенные
в некоторой конечной области сторонние токи плотности j. При постановке начально-краевой
задачи относительно векторов Е и Н будем исходить из системы
уравнений Максвелла, материальных уравнений, а также из того факта, что краевое
условие для тангенциальной составляющей вектора Е на границе между
киральной средой и идеальным проводником имеет такой же вид, как и в случае
границы между обычной средой и проводником. В результате приходим к следующей
начально-краевой задаче:
имеются сосредоточенные
в некоторой конечной области сторонние токи плотности j. При постановке начально-краевой
задачи относительно векторов Е и Н будем исходить из системы
уравнений Максвелла, материальных уравнений, а также из того факта, что краевое
условие для тангенциальной составляющей вектора Е на границе между
киральной средой и идеальным проводником имеет такой же вид, как и в случае
границы между обычной средой и проводником. В результате приходим к следующей
начально-краевой задаче:
Начально-краевая задача: обобщённая постановка.
Пусть ![]() , где
, где ![]() и
и ![]() – произвольные гладкие трёхкомпонентные
функции, обращающиеся в нуль при
– произвольные гладкие трёхкомпонентные
функции, обращающиеся в нуль при ![]() , такие что они сами и их первые производные
квадратично интегрируемы в
, такие что они сами и их первые производные
квадратично интегрируемы в ![]() . Умножим обе части уравнения (11) скалярно
в
. Умножим обе части уравнения (11) скалярно
в ![]() на функцию
на функцию ![]() и обе части уравнения (12)
на функцию
и обе части уравнения (12)
на функцию ![]() ,
сложим полученные равенства и проинтегрируем результат по времени от 0 до Т:
,
сложим полученные равенства и проинтегрируем результат по времени от 0 до Т:
![]()
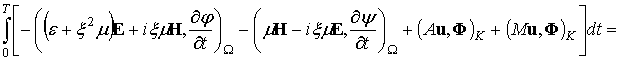
 , (15)
, (15)
где ![]() . В формуле (15) использованы обозначения
для скалярных произведений
. В формуле (15) использованы обозначения
для скалярных произведений
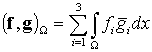
и
![]() ,
, ![]() ,
, ![]() ,
,
а также операторов
![]() ,
,
![]() .
.
Введем гильбертово пространство
![]()
и рассмотрим множество:
![]() .
.
Справедливы следующие леммы:
Лемма 1. Область ![]() плотна в K, и оператор A замкнут.
плотна в K, и оператор A замкнут.
Замечание 1. ![]() , если и только если выполняются условия:
, если и только если выполняются условия:
![]()
Лемма 2. Пусть граница ![]() области
области ![]() регулярна и ограничена. Тогда
любой элемент
регулярна и ограничена. Тогда
любой элемент ![]() ,
такой что форма
,
такой что форма ![]() непрерывна
на
непрерывна
на ![]() , принадлежит
области
, принадлежит
области ![]() , и
справедливо равенство
, и
справедливо равенство
![]() (16)
(16)
для любого ![]() .
.
Используя лемму 2, можно сформулировать обобщенную постановку исходной задачи следующим образом:
Необходимо
найти функцию ![]() ,
удовлетворяющую равенству
,
удовлетворяющую равенству
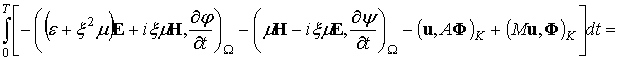
при любой функции Ф, такой что
![]()
и обращающейся в нуль
при ![]() , где
, где ![]() и
и ![]() .
.
Леммы 1 и 2 позволяют на основании метода Галеркина доказать существование и единственность слабого решения задачи:
Теорема 1. Если граница ![]() области
области ![]() регулярна и ограничена, то решение
задачи (17) существует, и оно единственно.
регулярна и ограничена, то решение
задачи (17) существует, и оно единственно.
Заключение.
В работе предложен алгоритм исследования экранированных резонаторов, заполненных киральным веществом. В качестве иллюстративного примера рассмотрен сферический киральный резонатор, для которого получены выражения для собственных полей и характеристическое уравнение для собственных частот. Проведенный анализ показал, что в киральном резонаторе могут формироваться только гибридные собственные поля, которые при обращении в нуль параметра киральности вырождаются в обычные E- и H-колебания. Собственные частоты кирального резонатора оказываются меньше соответствующих частот резонатора, заполненного обычной средой.
Также показано, что задача о возбуждении сторонними источниками электромагнитных колебаний в области с неоднородным киральным заполнением, ограниченной идеально проводящей поверхностью, либо являющейся дополнением к ограниченному идеальному проводнику, имеет единственное обобщенное решение. При доказательстве существования решения применен метод Галеркина, который может быть использован в дальнейшем для построения приближенного решения. Полученные результаты являются обобщением на случай киральной среды классических результатов о существовании и единственности решения задач дифракции электромагнитных волн на неоднородностях в среде, которая описывается обычными материальными уравнениями.
Литература
1. Боголюбов А.Н., Мосунова Н.А., Петров Д.А. // Математическое моделирование. 2007. 19, № 5. C.3
2. Кацеленбаум Б.З., Коршунова Е.Н., Сивов А.Н., Шатров А.Д. // Phys. Usp. 1997. 40, 1201.
3. Pelet P. // IEEE Transactions on Antennas and Propagation. 1990. 38, №1. P.90
4. Bahr A.J., Clausing K.R. // IEEE Trans. on antennas and propagation. 1994. 42, № 12. P. 1592
5. Jaggard D.L., Mickelson A.R. NJ: Princeton Univ. Press. 1952.
6. Tobar M.E., Mann A.G. // IEEE Trans. Microwave Theory Tech. 1991. 39, P. 2077.
7. Guillon P., Jiao X. // Proc. IEE. Part H. 1987. 134
8. Schiller S., Beyer R.L. // Opt.Lett. 1991. 16, P. 1138
9. Фел С.С., Левинсон И.Б., Фридберг П.Ш. // Радиофизика и электроника. 1962. 6, №11. C. 1125.
10. Julien A., Guillon P. // IEEE Trans. Microwave Theory Tech. 1986. 34, P.723
11. Tobar M.E., Anstie J.D., Hartnett J.G. // IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 2003. 50, № 11. P. 1407
12. Фукс Б.А. Введение в теорию аналитических функций многих комплексных переменных. М., гос. изд. физ.-мат. лит. 1962.
13. Моденов В.П., Цветков И.В.// Вестник Московского университета. Серия 3. Физика. Астрономия. 2004. №3. С. 8.
14. Ильинский А.С., Кравцов В.В., Свешников А.Г. Математические модели электродинамики. М.: “Высшая школа” 1991.
15. Г. Дюво, Ж.-Л. Лионс Неравенства в механике и физике. Москва “Наука”, Главная редакция физико-математической литературы, 1980.
 (7)
(7)