УДК 621.396.67
ДЕТЕКТИРОВАНИЕ СИГНАЛА В ИЗЛУЧАЮЩЕМ НЕЛИНЕЙНОМ ЭЛЕКТРОМАГНИТНОМ КРИСТАЛЛЕ
С. Е. Банков
Институт радиотехники и электроники им. В.А. Котельникова РАН, Москва
Получена 9 ноября 2011 г.
Аннотация. Рассмотрено взаимодействие электромагнитных волн в бесконечном излучающем электромагнитном кристалле, элементы которого содержат резистивно – емкостные нелинейные двухполюсники, являющиеся моделью полупроводниковых диодов. Исследуется одночастотное возбуждение структуры плоской волной, падающей из свободного пространства. Совместно решается граничная электродинамическая задача для поля внутри электромагнитного кристалла и нелинейная задача для напряжений и токов на нелинейных двухполюсниках. Излучающие элементы описываются приближенно без учета их взаимного влияния. Представлены результаты аналитического и численного исследования детектирования сигнала, созданного волной свободного пространства. Структура оптимизируется по критерию минимизации потерь преобразования. Показано, что излучающий нелинейный электромагнитный кристалл в режиме детектирования может обладать высокой направленностью не связанной с его геометрическими размерами.
Ключевые слова: электромагнитный кристалл, нелинейная антенная решетка, детектирование сигнала.
Abstract. Interaction of electromagnetic waves in infinite radiating electromagnetic crystal which elements contain nonlinear resistive-capacitive two-ports is considered. The structure is excited by a free space plane wave at dominant frequency. Boundary problem for fields inside electromagnetic crystal is simultaneously solved with a nonlinear problem for currents and voltages at nonlinear two-ports. Radiating elements are described approximately without consideration of their mutual coupling. Results of numerical and analytical study of detection of signal produced by free space plane wave are presented. The structure is optimized by a criterion of transformation loss minimum. It is shown that electromagnetic crystal in detection regime may have high directivity not connected with its geometrical dimensions.
Keywords: electromagnetic crystal, non-linear antenna array, signal detection.
1. Постановка задачи
Излучающие нелинейные электромагнитные кристаллы (ЭМК) представляют собой двумерно – периодические волноведущие структуры, которые содержат нелинейные элементы и имеют связь со свободным пространством. Примером такого ЭМК может служить рассмотренная в работе [1] решетка металлических цилиндров с нелинейными двухполюсниками, которая расположена внутри плоского волновода (ПВ). Под ПВ понимаем два бесконечных параллельных металлических экрана. Связь со свободным пространством обеспечивается решеткой излучателей, которые располагаются над ПВ и связаны с металлическими цилиндрами через отверстия в верхнем экране ПВ.
Таким образом, излучающий ЭМК данного типа представляет собой антенную решетку, которая может возбуждаться по-разному. Возбуждение может осуществляться, например, из свободного пространства. В простейшем случае источником возбуждения служит плоская волна, падающая на ЭМК.
Также ЭМК данного типа может возбуждаться волнами ПВ, а также комбинацией волн ПВ и свободного пространства. В работе [1] рассматривались разные способы возбуждения излучающего ЭМК с емкостными двухполюсниками. При этом было установлено, что важным фактором, существенно влияющим на свойства исследуемой структуры является взаимодействие волн свободного пространства с собственными волнами нелинейного ЭМК, которые распространяются внутри него. Резкое усиление степени нелинейного взаимодействия возникает в режиме пространственного синхронизма [2] волн, распространяющихся на кратных частотах.
В работе [1] было
показано, что нелинейный ЭМК в режиме пространственного синхронизма может
выполнять функцию высокоэффективной нелинейной антенны. Такая антенна
преобразует сигнал, поступающий из свободного пространства на основной частоте ![]() в сигнал удвоенной
частоты
в сигнал удвоенной
частоты ![]() . При этом
диаграмма направленности (ДН) ЭМК в приемном режиме оказывается уже ДН линейной
антенны тех же электрических размеров на частоте
. При этом
диаграмма направленности (ДН) ЭМК в приемном режиме оказывается уже ДН линейной
антенны тех же электрических размеров на частоте ![]() . Поэтому мы можем говорить об эффекте
сверхнаправленности, который достигается при приеме сигналов нелинейным ЭМК.
. Поэтому мы можем говорить об эффекте
сверхнаправленности, который достигается при приеме сигналов нелинейным ЭМК.
В той же работе [1]
показано, что одновременное возбуждение ЭМК волнами свободного пространства на
частоте ![]() и
волнами ПВ на частоте
и
волнами ПВ на частоте ![]() обеспечивает
прием волн с одновременным их параметрическим усилением.
обеспечивает
прием волн с одновременным их параметрическим усилением.
Явление пространственного синхронизма характерно для ЭМК, который является специфической средой, в которой могут распространяться электромагнитные волны. Поэтому излучающие ЭМК существенно отличаются от антенных решеток, нагруженных нелинейными двухполюсниками. Подобные решетки рассматривались в работах [3 – 5].
Данное исследование
является развитием работы [1]. В нем будет рассматрен ЭМК с резистивно –
емкостными двухполюсниками. Такой элемент может служить моделью
полупроводниковых диодов, которые широко распространенны на СВЧ. Основным
отличием резистивно – емкостного двухполюсника от емкостного является
возможность преобразования сигнала частоты ![]() на нулевую частоту или на постоянный ток.
Такой тип нелинейного преобразования известен под названием детектирование. Он
широко распространен в радиотехнике. В данной работе исследуется детектирование
сигналов, создаваемых волной свободного пространства, падающей на ЭМК. При этом
мы предполагаем, что по постоянному току каждый нелинейный элемент связан со
своей нагрузкой, в которой выделяется полезный сигнал. В этом случае эффекты,
обусловленные конечной длиной ЭМК играют второстепенную роль, если он имеет
достаточно большие электрические размеры. Поэтому для анализа таких структур
выбрана модель в виде бесконечного по двум координатам ЭМК, которая позволяет
существенно упростить решение задачи.
на нулевую частоту или на постоянный ток.
Такой тип нелинейного преобразования известен под названием детектирование. Он
широко распространен в радиотехнике. В данной работе исследуется детектирование
сигналов, создаваемых волной свободного пространства, падающей на ЭМК. При этом
мы предполагаем, что по постоянному току каждый нелинейный элемент связан со
своей нагрузкой, в которой выделяется полезный сигнал. В этом случае эффекты,
обусловленные конечной длиной ЭМК играют второстепенную роль, если он имеет
достаточно большие электрические размеры. Поэтому для анализа таких структур
выбрана модель в виде бесконечного по двум координатам ЭМК, которая позволяет
существенно упростить решение задачи.
2. Модель нелинейного ЭМК
В этом разделе будут получены уравнения, описывающие
исследуемую структуру. Схематично она показана на рис. 1. Более подробно период
ЭМК показан на рис. 2. В качестве излучателя, связывающего ЭМК со свободным
пространством на рис. 2 показан печатный излучатель, имеющий резонансные
свойства. Излучатели связаны с цилиндрами, образующими ЭМК через отверстия в
верхнем экране плоского волновода (ПВ), который образован двумя параллельными
металлическими плоскостями, расположенными на расстоянии ![]() друг от друга. Металлические
цилиндры радиуса
друг от друга. Металлические
цилиндры радиуса ![]() имеют
зазоры, в которые включены нелинейные двухполюсники.
имеют
зазоры, в которые включены нелинейные двухполюсники.
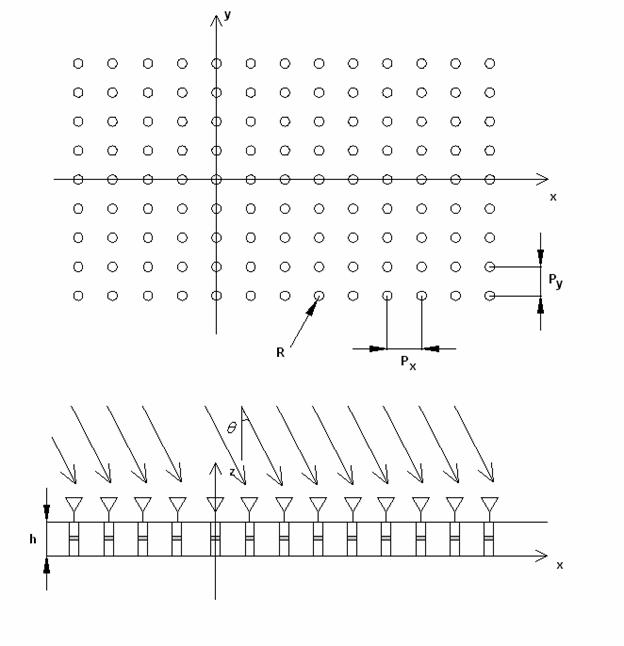
Рис. 1. Исследуемая структура.
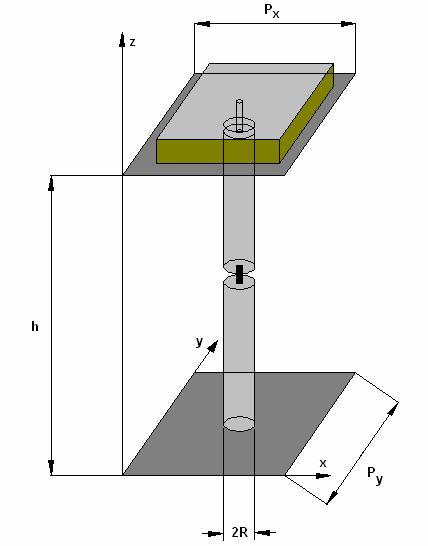
Рис. 2. Период исследуемой структуры.
Очевидно, что реальный ЭМК должен иметь конечные размеры по обеим координатам. Использование модели в виде бесконечной решетки оправданно тем, что для идеализированной структуры решение граничной задачи существенно упрощается. Это упрощение в линейных задачах достигается путем использования теоремы Флоке [6], позволяющей анализировать один период. Переход к анализу одного периода оправдан вследствие того, что электромагнитное поле удовлетворяет условиям квазипериодичности:
![]() , (1)
, (1)
где ![]() - фазовые постоянные, определяемые
условиями возбуждения периодической структуры. В нашем случае, когда она
возбуждается плоской волной свободного пространства,
- фазовые постоянные, определяемые
условиями возбуждения периодической структуры. В нашем случае, когда она
возбуждается плоской волной свободного пространства, ![]() имеют смысл проекций волнового
вектора этой волны на оси 0х и 0у соответственно:
имеют смысл проекций волнового
вектора этой волны на оси 0х и 0у соответственно:
![]() , (2)
, (2)
![]() ,
,
где ![]() - волновое число свободного пространства,
а
- волновое число свободного пространства,
а ![]() - углы в
сферической системе координат, задающие направление распространения плоской
волны. Угол
- углы в
сферической системе координат, задающие направление распространения плоской
волны. Угол ![]() ,
как обычно, отсчитывается от оси 0z, а угол
,
как обычно, отсчитывается от оси 0z, а угол ![]() от
оси 0х.
от
оси 0х.
Из соотношения (1) видно,
что нам достаточно найти поле в периоде с ![]() , а в других периодах его можно найти,
используя указанную формулу. Условие квазипериодичности записано для
комплексных амплитуд поля. Поэтому его можно использовать в виде (1) только для
линейных структур, в которых воздействие на частоте
, а в других периодах его можно найти,
используя указанную формулу. Условие квазипериодичности записано для
комплексных амплитуд поля. Поэтому его можно использовать в виде (1) только для
линейных структур, в которых воздействие на частоте ![]() создает отклик на той же
частоте. В нелинейном случае отклик имеет характер периодической функции с
периодом
создает отклик на той же
частоте. В нелинейном случае отклик имеет характер периодической функции с
периодом ![]() ,
которую можно разложить в ряд Фурье и описать с помощью гармоник на частотах
,
которую можно разложить в ряд Фурье и описать с помощью гармоник на частотах ![]() ,
, ![]() .
.
Модифицируем условие квазипериодичности для нелинейной структуры:
где под ![]() мы понимаем гармонику номера
мы понимаем гармонику номера ![]() любой величины,
описывающей электромагнитное поле и связанные с ним параметры: токи, напряжения
и т.д. Покажем далее, что условие (3) удовлетворяется при нелинейных
преобразованиях.
любой величины,
описывающей электромагнитное поле и связанные с ним параметры: токи, напряжения
и т.д. Покажем далее, что условие (3) удовлетворяется при нелинейных
преобразованиях.
Для простоты считаем, что ![]() . Пусть
. Пусть ![]() и
и ![]() - гармоники напряжения и тока на
нелинейных двухполюсниках, где
- гармоники напряжения и тока на
нелинейных двухполюсниках, где ![]() - номер элемента решетки, определяющий его
положение по оси 0х. Гармоники тока на нелинейном двухполюснике связаны с
напряжением следующим образом:
- номер элемента решетки, определяющий его
положение по оси 0х. Гармоники тока на нелинейном двухполюснике связаны с
напряжением следующим образом:
![]() ,
,
 ,
,
где ![]() - функция, описывающая нелинейные свойства
двухполюсника,
- функция, описывающая нелинейные свойства
двухполюсника, ![]() выбирается
произвольно на интервале от нуля до
выбирается
произвольно на интервале от нуля до ![]() . Подставим условие квазипериодичности для
напряжений
. Подставим условие квазипериодичности для
напряжений ![]() аналогичное
(3) в соотношение (4):
аналогичное
(3) в соотношение (4):
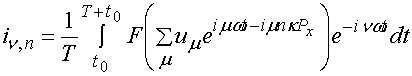 . (5)
. (5)
Осуществим замену переменной интегрирования в (5):
![]() , (6)
, (6)
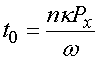 .
.
С учетом преобразования (6) соотношение (5) приобретает следующий вид:
![]() , (7)
, (7)
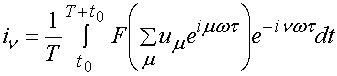 .
.
Равенство (7) доказывает справедливость условия квазипериодичности (3) для токов и напряжений на нелинейном двухполюснике. Поскольку все остальные элементы структуры линейны, то это означает справедливость условия (3) для всей структуры в целом.
Модель излучателя возьмем в том же виде, что и в работе [1], пренебрегая взаимной связью излучателей в решетке. Указанная модель представляет излучатель в виде сосредоточенной схемы (см. рис. 3), которая включена между металлическим цилиндром и верхним экраном ПВ.
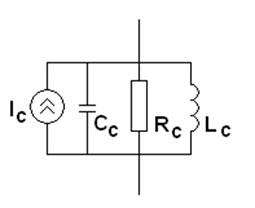
Рис. 3. Модель излучателя в виде параллельного контура.
Схема представляет собой параллельный контур вместе с источником тока, который описывает возбуждение плоской волной:
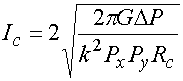 ,
(8)
,
(8)
где ![]() - коэффициент усиления излучателя,
- коэффициент усиления излучателя,
![]() - мощность
плоской волны, падающая на один период структуры. Отметим, что максимальный
коэффициент усиления
- мощность
плоской волны, падающая на один период структуры. Отметим, что максимальный
коэффициент усиления ![]() апертурной
антенны площадью
апертурной
антенны площадью ![]() описывается
соотношением [7]:
описывается
соотношением [7]:
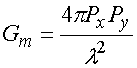 , (9)
, (9)
где ![]() - длина волны в свободном
пространстве. Коэффициент усиления (9) имеет площадка с равномерным
распределением источников. Источник тока
- длина волны в свободном
пространстве. Коэффициент усиления (9) имеет площадка с равномерным
распределением источников. Источник тока ![]() , соответствующий элементу решетки в виде
идеальной антенны имеет следующий вид:
, соответствующий элементу решетки в виде
идеальной антенны имеет следующий вид:
Нетрудно убедиться, что
максимальная мощность, которую можно передать от источника тока (10) в
согласованную с ним нагрузку равна мощности плоской волны, падающей на период
решетки ![]() .
.
Модель нелинейного двухполюсника возьмем в стандартной для СВЧ диодов форме [8]. Ее соответствует эквивалентная схема, показанная на рис. 4.
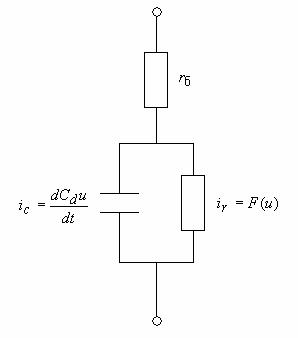
Рис. 4. Эквивалентная схема нелинейного двухполюсника.
Емкость диода ![]() зависит от напряжения
на нем:
зависит от напряжения
на нем:
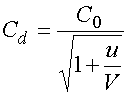 , (11)
, (11)
где ![]() - напряжение пробоя.
- напряжение пробоя.
Сопротивление диода описывается воль – амперной характеристикой:
![]() , (12)
, (12)
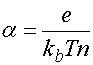 ,
,
где ![]() - постоянная Больцмана, Т –
абсолютная температура,
- постоянная Больцмана, Т –
абсолютная температура, ![]() - заряд электрона,
- заряд электрона, ![]() - параметр, зависящий от типа
диода,
- параметр, зависящий от типа
диода, ![]() -
обратный ток диода.
-
обратный ток диода.
Важным моментом является связь диода с внешней схемой на постоянном и переменном токах.

Рис. 5. Схема включения диода на постоянном токе.
На рис. 5 показана
схема включения диода на постоянном токе. Отметим, что сопротивление излучателя
согласно схеме на рис. 3 обращается в нуль. Также нулевое сопротивление имеет
металлический цилиндр, в который включен нелинейный двухполюсник. Связь диода с
внешней схемой происходит через фильтр, который на гармониках основной частоты
имеет бесконечной сопротивление и изолирует диод от сопротивления нагрузки ![]() и источника напряжения
смещения
и источника напряжения
смещения ![]() . В
этом случае период структуры можно представить, как показано на рис. 6.
. В
этом случае период структуры можно представить, как показано на рис. 6.
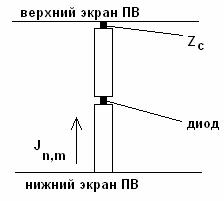
Рис. 6. Схема периода структуры на переменном токе.
На постоянном токе фильтр имеет нулевое сопротивление и соединяет диод с нагрузкой и источником смещения.
В работах [1], [2]
представлена методика вывода основного уравнения, описывающего периодическую
структуру конечной длины по координате ![]() и бесконечной по координате
и бесконечной по координате ![]() . Приведем его для
нашего случая без подробного вывода:
. Приведем его для
нашего случая без подробного вывода:
![]() , (13)
, (13)
где ![]() - вектор напряжений на
нелинейных частях сопротивлений диодов, находящихся в элементах решетки с
номерами
- вектор напряжений на
нелинейных частях сопротивлений диодов, находящихся в элементах решетки с
номерами ![]() .
. ![]() - вектор источников
тока в тех же элементах,
- вектор источников
тока в тех же элементах, ![]() - диагональная матрица, на главной
диагонали которой стоят сопротивления контуров
- диагональная матрица, на главной
диагонали которой стоят сопротивления контуров ![]() , моделирующих излучатели решетки,
, моделирующих излучатели решетки, ![]() ,
, ![]() - диагональная матрица,
составленная из сопротивлений
- диагональная матрица,
составленная из сопротивлений ![]() ,
, ![]() - матрица, описывающая взаимодействие элементов
решетки через волны ПВ,
- матрица, описывающая взаимодействие элементов
решетки через волны ПВ, ![]() - вектор, в который входят нелинейные
операторы, связывающие ток через диод с напряжением на его нелинейной части
- вектор, в который входят нелинейные
операторы, связывающие ток через диод с напряжением на его нелинейной части ![]() . Индекс
. Индекс ![]() показывают, что данная
величина соответствует гармонике основной частоты с номером
показывают, что данная
величина соответствует гармонике основной частоты с номером ![]() .
.
Уравнения (13) можно
обобщить также для постоянного тока (![]() ). Однако, имеет смысл переписать его для
этого случая отдельно:
). Однако, имеет смысл переписать его для
этого случая отдельно:
![]() , (14)
, (14)
где ![]() - вектор напряжений источников
смещений,
- вектор напряжений источников
смещений, ![]() -
диагональная матрица, элементы которой равны
-
диагональная матрица, элементы которой равны ![]() .
.
Матрица ![]() приводится в работах
[1,2]. В явном виде она нам не потребуется далее. Отметим только, что она
является матрицей Теплица, элементы которой зависят от разности индексов
приводится в работах
[1,2]. В явном виде она нам не потребуется далее. Отметим только, что она
является матрицей Теплица, элементы которой зависят от разности индексов ![]() .
.
Система уравнений (13)
справедлива, как отмечалось выше, для структуры конечной по оси 0х. Учтем далее
ее бесконечные размеры с помощью условия (3). Для этого подставим условия
квазипериодичности для напряжений ![]() в (13). При этом ограничимся случаем
в (13). При этом ограничимся случаем ![]() , который соответствует
падению волны в плоскости XOZ (
, который соответствует
падению волны в плоскости XOZ (![]() ). Произвольный угол падения
). Произвольный угол падения ![]() не дает нового
физического содержания в нашем приближении, а его учет усложняет математические
выкладки.
не дает нового
физического содержания в нашем приближении, а его учет усложняет математические
выкладки.
Описанные выше преобразования позволяют получить следующие соотношения:
![]() ,
, ![]() , (15)
, (15)
![]() ,
, ![]() ,
,
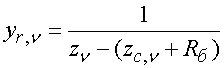 ,
,
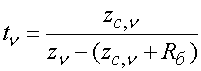 ,
,
где ![]() - комплексное сопротивление
излучателя на частоте
- комплексное сопротивление
излучателя на частоте ![]() ,
,
![]() - гармоника
напряжения на нелинейной части диода в элементе решетки с нулевым номером
- гармоника
напряжения на нелинейной части диода в элементе решетки с нулевым номером ![]() . Для сопротивления
. Для сопротивления ![]() из работ [1,2] получаем
следующее соотношение:
из работ [1,2] получаем
следующее соотношение:
 (16)
(16)
![]() ,
,
![]() ,
,
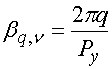 ,
,
где ![]() - волновое число свободного
пространства на частоте
- волновое число свободного
пространства на частоте ![]() ,
, ![]() - логарифмическая постоянная Эйлера,
- логарифмическая постоянная Эйлера, ![]() - постоянная, которую
выбирают из условия:
- постоянная, которую
выбирают из условия:
![]() . (17)
. (17)
Оператор ![]() , стоящий в уравнениях
(15), аналогичен интегральному оператору (4). Он выражает гармоники тока через
гармоники напряжения.
, стоящий в уравнениях
(15), аналогичен интегральному оператору (4). Он выражает гармоники тока через
гармоники напряжения.
Из уравнений (15)
видно, что условия квазипериодичности позволили нам свести анализ структуры к
анализу одного периода. Сделаем еще ряд допущений, облегчающий дальнейший
анализ структуры. Считаем, что контур, описывающий излучатель достаточно
добротный и настроенный на частоту ![]() , то есть на частоту падающей волны.
Предположение о высокой добротности контура позволяет считать его сопротивление
, то есть на частоту падающей волны.
Предположение о высокой добротности контура позволяет считать его сопротивление
![]() равным нулю
для всех гармоник кроме первой. С учетом этого индекс
равным нулю
для всех гармоник кроме первой. С учетом этого индекс ![]() в обозначении сопротивления
излучателя можно опустить.
в обозначении сопротивления
излучателя можно опустить.
Аналогично
необходимость в использовании индекса ![]() в обозначении источника тока отсутствует,
так как он отличен от нуля только на основной гармонике. Допущение о точной
настройке контура на частоту падающей волны позволяет записать:
в обозначении источника тока отсутствует,
так как он отличен от нуля только на основной гармонике. Допущение о точной
настройке контура на частоту падающей волны позволяет записать:
![]() . (18)
. (18)
Также необходимо
отметить, что сопротивление ![]() является мнимой величиной, которую удобно
представить в следующем виде:
является мнимой величиной, которую удобно
представить в следующем виде:
![]() . (19)
. (19)
Реактивное
сопротивление ![]() при
данной записи параметра
при
данной записи параметра ![]() имеет смысл сопротивления, которое вносят
все элементы решетки в импеданс элемента с нулевым номером.
имеет смысл сопротивления, которое вносят
все элементы решетки в импеданс элемента с нулевым номером.
Зададим далее параметр,
описывающий эффект детектирования. Будем использовать для этого коэффициент
передачи по мощности ![]() :
:
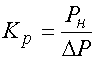 , (20)
, (20)
где ![]() - полезная мощность, выделяемая
в сопротивлении нагрузки. Остановимся далее на вычислении полезной мощности.
- полезная мощность, выделяемая
в сопротивлении нагрузки. Остановимся далее на вычислении полезной мощности.
Рассмотрим первое
уравнение системы (15). Отметим, что при ![]() ,
, ![]() оно имеет ненулевое решение относительно
оно имеет ненулевое решение относительно ![]() . Назовем его
. Назовем его ![]() . Очевидно, что это
напряжение не может быть полезным сигналом, так как оно никак не связано с
мощностью падающей волны. Это ни что иное как напряжение смещение, возникающее
на диоде благодаря источнику
. Очевидно, что это
напряжение не может быть полезным сигналом, так как оно никак не связано с
мощностью падающей волны. Это ни что иное как напряжение смещение, возникающее
на диоде благодаря источнику ![]() . Величина
. Величина ![]() является корнем следующего уравнения:
является корнем следующего уравнения:
![]() . (21)
. (21)
При подаче на диод
высокочастотного сигнала постоянное напряжение ![]() на нем будет отличаться от
на нем будет отличаться от ![]() :
:
![]() . (22)
. (22)
Полезным сигналом на
постоянном токе является добавка к напряжению смещения ![]() . С учетом этого замечания
коэффициент передачи (20) записывается следующим образом:
. С учетом этого замечания
коэффициент передачи (20) записывается следующим образом:
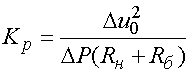 . (23)
. (23)
Коэффициент передачи, выраженный в децибелах носит название потерь преобразования, которые мы также будем использовать для описания детектирующих свойств структуры.
3. Аналитическое исследование ЭМК
Ниже будут представлены результаты аналитического исследования решения системы нелинейных уравнений (15). Для того чтобы получить это решение необходимо дополнительно упростить постановку задачи.
Предположим, что сигнал, падающий на структуры является сигналом малой интенсивности и диоды ЭМК функционируют в квадратичном режиме. В этом случае основным нелинейным эффектом является преобразование сигнала основной частоты в постоянный ток. Генерация высших гармоник также имеет место, но эти гармоники имеют более высокий порядок малости, чем сигнал на постоянном токе и ими можно пренебречь при исследовании процесса детектирования.
Далее, воспользуемся линейной аппроксимацией зависимости емкости от напряжения, которая соответствует квадратичному закону, описывающему емкостной ток:
![]() , (24)
, (24)
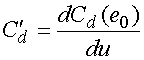 .
.
В квадратичном
режиме напряжение ![]() описывается
двумя гармониками: нулевой и первой, а система (15) содержит два уравнения:
описывается
двумя гармониками: нулевой и первой, а система (15) содержит два уравнения:
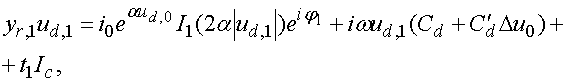
где ![]() - фаза напряжения
- фаза напряжения ![]() ,
, ![]() - модифицированные функции
Бесселя, возникающие в результате интегрирования вольт-амперной характеристики
диода.
- модифицированные функции
Бесселя, возникающие в результате интегрирования вольт-амперной характеристики
диода.
Будем искать решение
второго уравнения относительно напряжения первой гармоники в нулевом
приближении, то есть с точностью до членов порядка ![]() , а решение первого уравнения
относительно
, а решение первого уравнения
относительно ![]() ищем
с точностью до членов порядка
ищем
с точностью до членов порядка ![]() . Тогда раскладывая модифицированные
функции Бесселя в ряды Тейлора по малым аргументам, получаем:
. Тогда раскладывая модифицированные
функции Бесселя в ряды Тейлора по малым аргументам, получаем:
 , (26)
, (26)
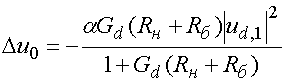 ,
,
![]() ,
,
![]() .
.
Подставим первое равенство (26), а также соотношение (10) во второе равенство (26):
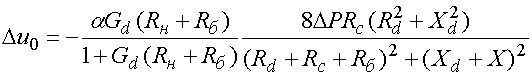 . (27)
. (27)
Коэффициент передачи ![]() выражается следующим
образом:
выражается следующим
образом:
 . (28)
. (28)
Параметр ![]() является функцией
нескольких свободных параметров. К их числу относятся: сопротивление излучателя
является функцией
нескольких свободных параметров. К их числу относятся: сопротивление излучателя
![]() ,
сопротивление нагрузки по постоянному току
,
сопротивление нагрузки по постоянному току ![]() , напряжение источника смещения
, напряжение источника смещения ![]() , реактивное
сопротивление
, реактивное
сопротивление ![]() ,
которое, в свою очередь, зависит от параметров ЭМК. Напряжение источника
смещения влияет на активную и реактивную составляющие проводимости диода
,
которое, в свою очередь, зависит от параметров ЭМК. Напряжение источника
смещения влияет на активную и реактивную составляющие проводимости диода ![]() . При этом влияние на
активную составляющую значительно более сильное. Небольшие вариации параметра
. При этом влияние на
активную составляющую значительно более сильное. Небольшие вариации параметра ![]() могут менять ее от
очень больших значений до очень маленьких благодаря экспоненциальной вольт –
амперной характеристике диода. Изменения реактивной составляющей при этом
существенно меньше. Параметры
могут менять ее от
очень больших значений до очень маленьких благодаря экспоненциальной вольт –
амперной характеристике диода. Изменения реактивной составляющей при этом
существенно меньше. Параметры ![]() и
и ![]() в большей степени определяются типом
диода. Поэтому в качестве независимого параметра мы можем использовать
в большей степени определяются типом
диода. Поэтому в качестве независимого параметра мы можем использовать ![]() вместо
вместо ![]() .
.
Найдем условия, при
которых коэффициент передачи ![]() достигает своего максимума. Данную
операцию нетрудно сделать по переменным
достигает своего максимума. Данную
операцию нетрудно сделать по переменным ![]() и
и ![]() . Для этого достаточно продифференцировать
функцию (28) по ним и найти значения
. Для этого достаточно продифференцировать
функцию (28) по ним и найти значения ![]() и
и ![]() , в которых указанные производные
обращаются в ноль:
, в которых указанные производные
обращаются в ноль:
 , (29)
, (29)
![]() .
.
Подстановка соотношений (29) в формулу (28) дает следующий результат:
 . (30)
. (30)
Введем следующие обозначения:
 , (31)
, (31)
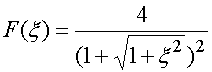 ,
,
![]() ,
, ![]() .
.
Обозначения (31) позволяют компактно записать выражение для коэффициента передачи:
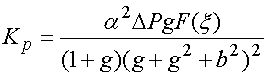 . (32)
. (32)
Функция ![]() имеет максимум при
имеет максимум при ![]() . В этой точке она равна
единице. Функция
. В этой точке она равна
единице. Функция ![]() :
:
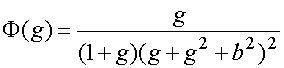 . (33)
. (33)
имеет максимум по переменной ![]() . Найти его аналитически
не представляется возможным. Однако для оптимального значения
. Найти его аналитически
не представляется возможным. Однако для оптимального значения ![]() можно предложить
аппроксимацию, дающую погрешность не превышающую 1.5% при
можно предложить
аппроксимацию, дающую погрешность не превышающую 1.5% при ![]() :
:
 , (34)
, (34)
![]() .
.
При малых значениях
параметра ![]() оптимальное
значение проводимости
оптимальное
значение проводимости ![]() дается
соотношением:
дается
соотношением:
![]() . (35)
. (35)
При выполнении
равенства (35) получаем максимальное значение функции ![]() :
:
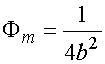 . (36)
. (36)
Соответственно запишем
выражение для максимального значения коэффициента передачи ![]() :
:
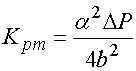 . (37)
. (37)
Функция ![]() описывает зависимость
коэффициента передачи структуры от угла падения плоской волны. Таким образом, ее
можно рассматривать как ДН нелинейного ЭМК. Ширина ДН определяется условием,
при котором функция
описывает зависимость
коэффициента передачи структуры от угла падения плоской волны. Таким образом, ее
можно рассматривать как ДН нелинейного ЭМК. Ширина ДН определяется условием,
при котором функция ![]() равна
0.5 от ее максимального значения. Значение параметра
равна
0.5 от ее максимального значения. Значение параметра ![]() , соответствующее данному условию
определяется соотношением:
, соответствующее данному условию
определяется соотношением:
![]() . (38)
. (38)
От угла падения волны ![]() зависит только функция
зависит только функция ![]() . В предположении, что
ДН имеет малую ширину ее можно разложить в ряд Тейлора в окрестности точки
. В предположении, что
ДН имеет малую ширину ее можно разложить в ряд Тейлора в окрестности точки ![]() :
:
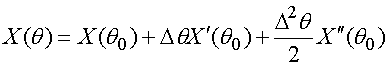 , (39)
, (39)
![]() ,
,
где ![]() ,
, ![]() - первая и вторая производные в точке
- первая и вторая производные в точке ![]() .
.
С учетом формул (39)
полная ширина ДН ![]() определяется
соотношением:
определяется
соотношением:
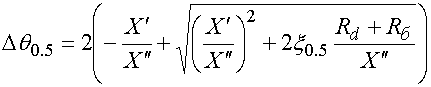 (40)
(40)
Функция ![]() является четной
функцией своего аргумента. Поэтому в точке
является четной
функцией своего аргумента. Поэтому в точке ![]() ее производная равна нулю. В этом случае
соотношение (40) можно упростить:
ее производная равна нулю. В этом случае
соотношение (40) можно упростить:
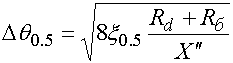 . (41)
. (41)
Если угол ![]() далек от нуля, то, как
правило, выполняется неравенство:
далек от нуля, то, как
правило, выполняется неравенство:
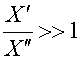 .
.
С его помощью получаем выражение для ширины ДН, имеющей главный луч, отклоненный от нормали:
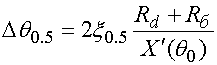 . (42)
. (42)
Перейдем в формулах (41), (42) к обозначениям (31):
 , (43)
, (43)
 .
.
Из соотношений (43)
видно, что при достаточно малом сопротивлении базы структура может иметь весьма
узкую ДН. Ее ширина ограничена конечным значением параметра ![]() . Отметим, что ширина ДН
увеличивается при приближении угла
. Отметим, что ширина ДН
увеличивается при приближении угла ![]() к нулевому значению, так как при
к нулевому значению, так как при ![]() =0 параметр
=0 параметр ![]() пропорционален
пропорционален ![]() , а при
, а при ![]() он пропорционален
он пропорционален ![]() .
.
Направленность нелинейного ЭМК в режиме детектирования отличается от направленности традиционных антенн, которая обусловлена когерентным сложением сигналов в одной точке. В традиционной антенне сигналы, поступившие на разные участки ее апертуры складываются на выходе антенны. Сложение может осуществляться с помощью сумматора мощности, как это делается в антенных решетках или с помощью оптической системы: зеркала или линзы. В этом случае сигналы суммируются в фокусе оптической системы. Идеальное сложение имеет место только для одного угла падения волны на антенну. При отклонении угла от оптимального происходит несинфазное сложение сигналов и мощность на выходе падает. Важно, что ширина ДН при указанном способе создания направленности зависит от размеров антенны. Чем они больше, тем уже ДН.
Из формулы (43) видно,
что размеры ЭМК не входят в соотношение для ширины ДН. Они в принципе не могут
туда входить, так как мы рассматриваем бесконечную структуру. Направленность
ЭМК связана с резонансными эффектами, которые могут возникать в каждом
отдельном его элементе. Условие ![]() соответствует условию компенсации
реактивной части сопротивления диода собственным сопротивлением выделенного
элемента ЭМК, а также вносимым сопротивлением соседних элементов решетки. Такая
компенсация реактивного сопротивления говорит о резонансном характере явлений,
происходящих в структуре. Особенностью ЭМК является то, что вносимое
сопротивление зависит от угла падения волны. Поэтому при его отклонении от
оптимального значения
соответствует условию компенсации
реактивной части сопротивления диода собственным сопротивлением выделенного
элемента ЭМК, а также вносимым сопротивлением соседних элементов решетки. Такая
компенсация реактивного сопротивления говорит о резонансном характере явлений,
происходящих в структуре. Особенностью ЭМК является то, что вносимое
сопротивление зависит от угла падения волны. Поэтому при его отклонении от
оптимального значения ![]() ,
на которое настроена структура происходит увеличении мнимой части импеданса,
которое неизбежно приводит к уменьшению выходного полезного сигнала.
,
на которое настроена структура происходит увеличении мнимой части импеданса,
которое неизбежно приводит к уменьшению выходного полезного сигнала.
Очевидно, что резонансные явления должны порождать не только резкую зависимость коэффициента передачи от угла падения, но и от частоты. Поэтому появление направленности должно сопровождаться уменьшением полосы рабочих частот.
Интерпретация
направленности ЭМК с позиций резонансных эффектов легко объясняет тот факт, что
предел уменьшению ширины ДН ставит конечное значение сопротивления диода ![]() . Указанное
сопротивление является источником диссипативных потерь в ЭМК при условии, что
все остальные его элементы таких потерь не имеют. Поэтому величина
. Указанное
сопротивление является источником диссипативных потерь в ЭМК при условии, что
все остальные его элементы таких потерь не имеют. Поэтому величина ![]() задает добротность
резонанса, которая при
задает добротность
резонанса, которая при ![]() =0 была бы бесконечно большой. Поэтому мы
видим из соотношения (43), что конечная добротность колебательной системы
приводит к конечной ширине ДН.
=0 была бы бесконечно большой. Поэтому мы
видим из соотношения (43), что конечная добротность колебательной системы
приводит к конечной ширине ДН.
4. Численное исследование ЭМК
Далее мы на
ряде количественных примеров рассмотрим закономерности, которые качественно
описывает приближенная модель, описанная в разд. 3. Изучим, в первую очередь,
поведение потерь преобразования ![]() (
(![]() ) от сопротивлений излучателя и нагрузки.
Как следует из разд. 3, должны существовать их оптимальные значения, при которых
величина
) от сопротивлений излучателя и нагрузки.
Как следует из разд. 3, должны существовать их оптимальные значения, при которых
величина ![]() максимальна.
максимальна.
На рис. 7 показана
зависимость потерь преобразования от сопротивления нагрузки ![]() . Она получена при
. Она получена при ![]() =500 Ом, f=7 ГГц,
=500 Ом, f=7 ГГц, ![]() ,
, ![]() пФ,
пФ, ![]() В,
В, ![]() В,
В, ![]() Вт,
Вт, ![]() ,
, ![]() ,
, ![]() . Все размеры здесь и далее приводятся в
миллиметрах. Из рис. 7 видно, что потери преобразования резко уменьшаются,
достигают минимума и сравнительно медленно нарастают. Таким образом, численные
расчеты подтверждают экстремальный характер зависимости параметра
. Все размеры здесь и далее приводятся в
миллиметрах. Из рис. 7 видно, что потери преобразования резко уменьшаются,
достигают минимума и сравнительно медленно нарастают. Таким образом, численные
расчеты подтверждают экстремальный характер зависимости параметра ![]() от сопротивления
нагрузки.
от сопротивления
нагрузки.

Рис. 7. Зависимость потерь преобразования от сопротивления нагрузки.
Аналогичная зависимость
потерь преобразования от сопротивления излучателя ![]() была получена при
была получена при ![]() Ом. Остальные параметры
структуры остались такими же, как и в первом примере. Указанная зависимость
показана на рис. 8.
Ом. Остальные параметры
структуры остались такими же, как и в первом примере. Указанная зависимость
показана на рис. 8.
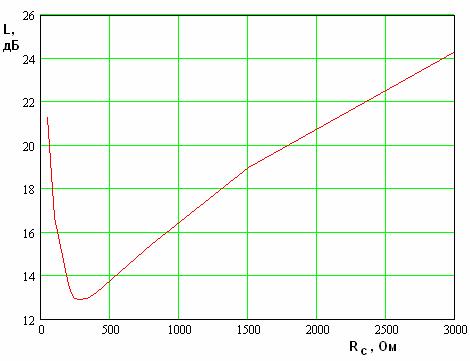
Рис. 8. Зависимость потерь преобразования от сопротивления излучателя.
На рис. 9 представлена
зависимость потерь преобразования от напряжения смещения. Она получена при тех
же параметрах, что и раньше, ![]() Ом.
Ом.
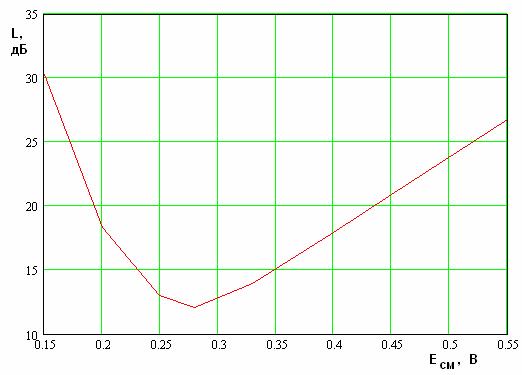
Рис. 9. Зависимость потерь преобразования от напряжения смещения на диоде.
Данная зависимость
также имеет экстремальный характер. Он соответствует экстремальной зависимости
потерь преобразования от активной части проводимости диода ![]() . Отметим, что абсолютные
значения оптимальных сопротивлений нагрузки и излучателя, а также напряжения
смещения сильно зависят от емкости диода при нулевом смещении
. Отметим, что абсолютные
значения оптимальных сопротивлений нагрузки и излучателя, а также напряжения
смещения сильно зависят от емкости диода при нулевом смещении ![]() . В качестве примера
приведем зависимость потерь преобразования от сопротивления излучателя при
. В качестве примера
приведем зависимость потерь преобразования от сопротивления излучателя при ![]() пФ. Она показана на
рис. 10. Кривая получена при
пФ. Она показана на
рис. 10. Кривая получена при ![]() В,
В, ![]() ,
, ![]() ,
, ![]() Ом. Другие параметры структуры не менялись.
Ом. Другие параметры структуры не менялись.

Рис.
10. Зависимость потерь преобразования от сопротивления излучателя при ![]() пФ.
пФ.
Из рис. 10 видно, что
увеличение емкости диода привело к существенному смещению минимума потерь
преобразования в сторону меньших значений ![]() .
.
Рассмотрим далее
направленные свойства структуры, которые будем описывать функцией ![]() :
:
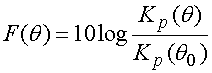 , (44)
, (44)
которая является нормированной
ДН. Под ![]() понимается
угол, при котором коэффициент передачи по мощности достигает максимального
значения.
понимается
угол, при котором коэффициент передачи по мощности достигает максимального
значения.
Интересно проследить
зависимость ширины ДН от емкости диода ![]() . На рис. 11 представлены три ДН,
соответствующие
. На рис. 11 представлены три ДН,
соответствующие ![]() =0.1,
1, 5 пФ.
=0.1,
1, 5 пФ.

Рис.
11. ДН ЭМК в режиме детектирования при разных значениях емкости ![]() .
.
Видно, что структура
настроена на ![]() =0.
Также мы можем отметить, что ширина ДН уменьшается с ростом емкости нелинейного
элемента. Такое поведение ДН можно объяснить ростом добротности резонатора,
который образуется в каждом периоде ЭМК. Увеличивая емкость мы увеличиваем
энергию, запасенную в резонаторе и, следовательно, увеличиваем его добротность.
Выше отмечалась связь между добротностью и направленностью структуры, которая
приводит к сужению ДН.
=0.
Также мы можем отметить, что ширина ДН уменьшается с ростом емкости нелинейного
элемента. Такое поведение ДН можно объяснить ростом добротности резонатора,
который образуется в каждом периоде ЭМК. Увеличивая емкость мы увеличиваем
энергию, запасенную в резонаторе и, следовательно, увеличиваем его добротность.
Выше отмечалась связь между добротностью и направленностью структуры, которая
приводит к сужению ДН.
На рис. 12 представлены
ДН ЭМК, иллюстрирующие разную настройку структуры. Кривые 1 и 2 получены при ![]() =5 пФ и
=5 пФ и ![]() =0,200.
Приближенная теория, представленная в разд. 3 предсказывает сужение ДН ЭМК при
его настройке на углы излучения отличные от нулевого. Численные расчеты
полностью подтверждают этот вывод. Из рис. 12 видно, что ДН 2 существенно уже
ДН 1, соответствующей
=0,200.
Приближенная теория, представленная в разд. 3 предсказывает сужение ДН ЭМК при
его настройке на углы излучения отличные от нулевого. Численные расчеты
полностью подтверждают этот вывод. Из рис. 12 видно, что ДН 2 существенно уже
ДН 1, соответствующей ![]() =0.
=0.

Рис.
12. ДН ЭМК при настройке на разные углы ![]() .
.
Заключение
Представленная выше работа продолжает серию работ [1,2,7,8], в которых рассматривались эффекты взаимодействия электромагнитных волн в нелинейном ЭМК. Особенностью рассмотренной периодической структуры является сильная связь между ее элементами, которая возникает благодаря возможности распространения волн в ЭМК. Этим она существенно отличается от нелинейных антенных решеток, в которых связь элементов существует, но не играет столь сильную роль, поскольку каналы решетки изолированы и связь происходит почти исключительно благодаря волнам свободного пространства. В данной работе показано, что сильная связь элементов ЭМК может быть инструментом, который позволяет создавать направленные антенны, работающие в режиме детектирования.
Такой вывод не является полностью очевидным. Традиционно направленность антенны принято связывать с описанными в разд. 3 эффектами когерентного сложения волн. В режиме детектирования когерентное сложение волн невозможно, так как полезный сигнал имеет нулевую частоту. Поэтому направленность, описанная в разд. 3 и 4 имеет другую резонансную природу. Важной отличительной чертой этого типа направленности является то, что ширина ДН напрямую не связана с геометрическими размерами антенны. При этом следует отметить, что данный вывод сделан на основе анализа бесконечной структуры. Для того, чтобы полностью убедиться в его достоверности, необходимо исследовать ЭМК конечных размеров. Возможно, что краевые эффекты, характерные для антенн конечных размеров скорректируют сделанный выше вывод.
Литература
1. Банков С.Е. Численное исследование двухчастотного взаимодействия волн в нелинейном излучающем электромагнитном кристалле // РЭ. 2011. Т. 56. № 9. С. 1044-1056.
2. Банков С.Е. Модель нелинейного электромагнитного кристалла // РЭ. 2011. Т.56. №3. С. 261.
3. Malyuskin A., Fusco V., Schuchinsky A. Microwave phase conjugation using nonlinerly loaded wire arrays // IEEE Trans. AP. 2006. V. 54. №1. P. 192-203.
4. Malyuskin A., Fusco V., Schuchinsky A. Phase conjugation wire FSS lens // IEEE Trans. AP. 2006. V.54. №5. P. 1399-1403.
5. Pon C.Y. Retrodirective array using the heterodyne technidue // IEEE Trans. AP. 1966. V. 12. №2. P. 176-180.
6. Сазонов В.П., Силин Р.А. Замедляющие системы. М.: Сов. Радио. 1966.
7. Банков С.Е. Численное исследование взаимодействия прямой и обратной волн в нелинейном электромагнитном кристалле // Успехи современной радиоэлектроники. 2011. №5. С. 31-43.
8. Банков С.Е. Аналитическое исследование двухчастотного взаимодействия прямой и обратной волн в нелинейном электромагнитном кристалле // РЭ. 2011. Т.56. №8. С. 909-919.
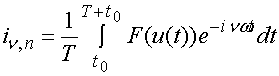 , (4)
, (4)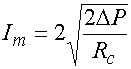 . (10)
. (10)