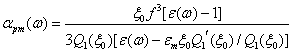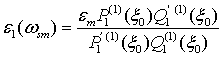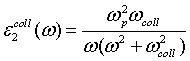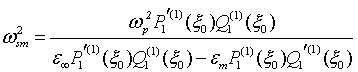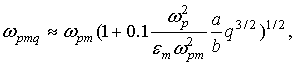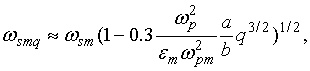МЕТАЛЛИЧЕСКИЕ НАНОСТРУКТУРЫ ДЛЯ ПОВЫШЕНИЯ ЭФФЕКТИВНОСТИ ВОЛОКОННО-ОПТИЧЕСКИХ УСИЛИТЕЛЕЙ С ИОНАМИ ЭРБИЯ ДЛЯ ДЛИНЫ ВОЛНЫ 1.54 МКМ

Г. А. Денисенко ^{1 , 2}, А. А. Курушин ³

¹ Учреждение Российской академии наук Институт кристаллографии имени А.В.Шубникова РАН, Москва

² Научно-исследовательский институт ядерной физики имени Д.В.Скобельцына , МГУ имени М.В.Ломоносова, Москва

³ Московский энергетический институт

Получена 23 января 2012 г.

Аннотация. Для исследования явления люминесценции адсорбированных сред с ионами редкоземельных элементов, обусловленного плазмонами, применены серебряные поверхности с расположенной на них системой наноразмерных острий, изготавливаемые с использованием трековых мембран. Даны основные соотношения, определяющие частоты плазмонных колебаний электронных систем острий, промоделированных полусфероидальными выступами. Проанализировано влияние на эти частоты взаимодействия между диполями, возникающими в остриях. Определены параметры систем серебряных наноострий для обеспечения усиления люминесценции сред с ионами эрбия, широко используемых в настоящее время в волоконно-оптических усилителях для длины волны 1.54 микрона. Получены и охарактеризованы экспериментальные образцы острийных наноструктур для проведения спектрально- люминесцентных измерений для случая сред, содержащих ионы европия. Выполнено численное моделирование частотных характеристик типичных острийных наноструктур методом конечных разностей во временной области FDTD. Полученные результаты расчетов на программе SCT Microwave Studio сравниваются с экспериментальными данными.

Ключевые слова: Редкоземельные ионы; серебряные наноразмерные острии; усилении люминисценции; волоконно-оптический усилитель; поверхностные плазмоны; численное моделирование оптических систем.

Abstract. Well-ordered metal structures, i.e. arrays of nanosized tips on silver surface for studies of the luminescence enhancement of absorbed media with rare earth ions were used. These arrays were prepared by the metal evaporation on track membranes. Calculations of resonance frequencies of tips regarded as semispheroids were done taking into account the interaction between dipoles of tips. Contemporary software for electrodynamics modeling can be applied to regard the mentioned above nanosized optical systems too. By using FDTD from CST Microwave Studio preliminary calculations for extinction cross section of silver tip arrays and other nanosized gold and silver metal structures have been performed. Distributions of the electromagnetic fields and different characteristics of the fields have been obtained.
Keywords: rare earth ions; silver nanosized tips; luminescence enhancement; optical amplifier; plasmon modes; numerical modelling of optical systems.

1. Введение

Конденсированные среды (стекла, кристаллы, неорганические пленки), легированные редкоземельными ионами (РЗИ), нашли широкое применение в качестве активных элементов лазерных устройств и волоконно-оптических усилителей, люминофоров, сцинтилляторов и люминесцентных концентраторов, повышающих КПД солнечных батарей. Поэтому, рассматриваются самые различные способы повышения эффективности таких устройств [1-5]. Одним из наиболее интересных, на данный момент, вопросов является возможность использовать с этой целью взаимодействие РЗИ с поверхностными плазмонами, возбуждаемыми в различных металлических наноструктурах [7-12]. В настоящее время значительное число публикаций по данному вопросу связано с исследованием усиления люминесценции РЗИ, обусловленного взаимодействием РЗИ с поверхностными плазмонами.

2. Теоретический анализ

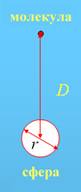
Для выяснения особенностей в усилении электромагнитного поля металлическими острийными наноструктурами рассмотрение будем вести в сравнении со случаем металлических сферических наночастиц. При этом будем использовать предположение, что характерные размеры острия или частицы меньше длины волны внешнего электромагнитного поля R<<l. Это позволяет рассматривать его действие на электроны проводимости металлического образования как простую поляризацию.

Рис. 1. Моделирование металлической сферы и эллипсоида, находящего в среде с проницаемостью ε_m.

Кроме того, мы будем рассматривать острия таких размеров, при которых еще можно использовать диэлектрическую проницаемость массивного металла.

Для поляризуемости a сферической частицы радиуса R в этом случае имеем [19]:

где и - диэлектрические проницаемости частицы и окружающей среды, соответственно, - частота падающей электромагнитной волны . Из (1) следует, что при определенных значениях поляризуемость наночастицы может возрасти. Поляризованная частица и сама начинает действовать как источник поля. Усиление электромагнитного поля в среде будет существенным при выполнении условия , то есть , где и - действительная и мнимая части диэлектрической проницаемости металла. Для этого должна быть отрицательной, а - малой величиной. С физической точки зрения здесь мы имеем резонансное возбуждение поверхностных плазмонов металлической наночастицы.

Диапазон длин волн, который охватывает как возбуждение, так и люминесценцию РЗИ, охватывает интервал 400 ¸1500 нм. Например, для европия представляет интерес длина волны, используемая для возбуждения люминесценции на переходе ⁷F₀®⁵L₆ ( 395 нм), и длина волны люминесценции на переходе ⁵D₀®⁷F₂ (сверхчувствительный переход) 615 нм [20].

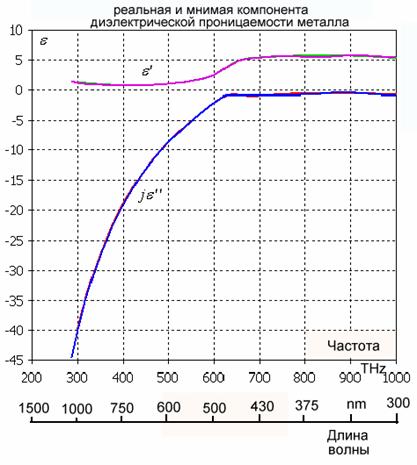
Указанным условиям хорошо отвечает случай серебра. На рис.2 приводятся зависимости действительной и мнимой части диэлектрической проницаемости серебра от длины волны, построенные нами, исходя из экспериментальных данных экспериментальных данных работы [21]. Резонансная частота, определяемая соотношением , при применении модели свободных электронов Друде равна: , где - плазменная частота. Так, для стекла 28Na₂O-78B₂O₃ (указаны мольные проценты), использованного в [10] , что расположит максимум полосы возбуждения на длине волны 419 нм (экспериментальное значение 415 нм).

В случае сферических наночастиц серебра при соблюдении исходного условия на их размеры подстройка частоты, на которой происходит усиление электромагнитного поля, как это следует из соотношения: , осуществляется только подбором среды по показателю преломления или специальным покрытием наночастиц. При обычных значениях показателя преломления среды (стекла, неорганические пленки, растворители) усиление электромагнитного поля может быть достигнуто в диапазоне 380430 нм. В [22] специальное использование аморфного кремния (показатель преломления 3.7) позволило сдвинуть пик поглощения к 770 нм. Из сказанного следует, что требуемого в ряде конкретных случаев дальнейшего существенного продвижения в длинноволновую область в случае сферических наночастиц таким способом достичь будет сложно. Поэтому для практической реализации в оптических усилителях шаровые вкрапины не дадут нужные результаты, и нужно создавать наноструктуры более сложной геометрической формы.

Рис. 2. Реальная и мнимая части диэлектрической проницаемости серебра в оптическом диапазоне.

В работах [13,14] для изучения явления усиления люминесценции РЗИ нами было предложено использовать металлические поверхности с системой расположенных на них наноразмерых острий серебра. Характеристики серебра даются на рис. 2. Среды с РЗИ наносятся на такие поверхности, подобно случаю с металлическими островковыми пленками. Особенностью данных металлических структур является повторяемость формы острий и их геометрических размеров, а также выдерживание одинаковой ориентации острий относительно поверхности. Это должно позволить проводить количественный анализ экспериментальных данных. Ввиду отсутствия процедуры восстановления металла исключена и возможность процессов сенсибилизации. (отметим, что это зависит от правильного приготовления образцов, процесса температурного отжига, химической активности остри и пр.). Трековые мембраны представляют собой полимерные пленки, облученные пучком тяжелых ионов в ускорителе [15]. Химическое травление позволяет получить поры конической формы в пленке на месте прохождения ионов. Последующее напыление металла (в данном случае, серебра) создает на металлической поверхности систему конических острий. Подобные металлические острийные наноструктуры используются для идентификации пикограммовых количеств органических и неорганических соединений с помощью ГКР и генерации гигантской второй гармоники [18]. Микрофотография одной из острийных серебряных наноструктур, полученных в процессе выполнения представляемой нами работы, дан на рис.3.

Рис. 3. Фотография реальной наноструктуры с острийными окончаниями.

Для острийных металлических структур настройка на нужную частоту дополнительно может достигать за счет создания острий со специально подбираемыми геометрическими параметрами.

Если не рассматривать острия со специально заостренными вершинами, то в достаточно хорошем приближении можно представить отдельное острие как сфероидальный выступ на металлической поверхности.

В работе [23] были рассмотрены собственные колебания плотности заряда вытянутого сфероида (эллипсоид вращения) с отношением полуосей a и b, >1. Эти результаты в силу симметрии применимы и к нашему случаю. Имеется три моды колебаний: аксиально-симметричная - вдоль главной оси сфероида (то есть в направлении перпендикулярном поверхности) и две вырожденные азимутально-симметричные. В отличие от случая сферических наночастиц здесь начинает играть роль поляризация света.

Для динамической поляризуемости сфероида с учетом нанесенной на его поверхность среды с диэлектрической проницаемостью в случае p-поляризации света (возбуждена аксиально-симметричная мода) применимо следующее выражение:

, (2)

где и - функции Лежандра первого и второго рода соответственно, , . Обозначение a_pm указывает, что поляризуемость зависит и от диэлектрической проницаемости среды, покрывающей острие.

Рис. 4. Вытянутый металлический сфероид и его резонансные моды.

Отсюда следует, что возникающая динамическая поляризация сфероида очень велика, если частота падающего излучения совпадает с частотой собственных аксиальных колебаний, определяемой из выражения:

, (3)

здесь, как и ранее, мы рассматриваем диапазон длин волн, в котором мнимая часть близка к нулю (случай серебра).

Таким образом, подбирая отношение полуосей сфероида и с учетом частотной зависимости действительной части диэлектрической проницаемости серебра, можно дополнительно сдвигать резонансную частоту.

Для поля в точке, расположенной на главной оси сфероида (координаты ) имеет место соотношение:

, (4)

где - коэффициент усиления поля.

Cобственные частоты азимутально-симметричных колебаний (возбуждаются s-поляризованным светом) определяются выражением:

. (5)

Естественно, различные процессы затухания поверхностных плазмонов, связанные (рассеяние электронов в наночастице на фононах, дефектах структуры и поверхности частицы) лимитируют достигаемое усиление электромагнитного поля. В рамках модели Друдде рассеяние электронов на поверхности металлической наноструктуры (наночастицы, острия) учитывается введением в мнимую часть диэлектрической восприимчивости члена, имеющего вид [24,25]:

, (6)

где частота столкновений , - скорость Ферми, - свободная длина пробега в массивном металле, - характерный размер металлической наноструктуры (для сферической наночастицы- 2, для сфероида- длина малой оси- ). Приведенная в[24] оценка для в серебре, равна 52 нм.

Перейдем теперь к случаю сплюснутого сфероида (a/b<1). Решения для этого случая могут быть получены из уравнений Лапласа при соответствующем выборе сфероидальных координат [26] с учетом условий поведения потенциала и его нормальной производной на границе сфероида. Фактически, это выразится в замене на , где i– мнимая единица в выражениях (3) и (5). Для случая азимутальных колебаний это было проведено в [27] в предположении, что для металла применима модель свободных электронов Друдде, и сфероид находится в вакууме.

Таким образом, исходя из экспериментальных данных по e(w) (речь идет о металлических структурах достаточно больших размеров, когда применимо использование такой величины), можно определить частоты собственных колебаний для сферической частицы и сфероидального выступа.

Отметим, что при получении выражений (1), (3) и (5) использовались лишь обычные условия непрерывности для нормальной и тангенциальной компонент напряженности электрического поля на границе двух сред и геометрические характеристики металлической структуры (сферичность, эллипсоидальность). Дальнейшее рассмотрение требует конкретизации в описании самой электронной системы данной структуры.

В простейшем случае, когда применима модель свободных электронов Друде и , указанные выражения существенно упрощаются. Однако в случае серебра в интересующей нас области длин волн значительную роль играют межзонные электронные переходы, существенно сказывающиеся на поведении диэлектрической проницаемости. Приведенные на рис.2 зависимости хорошо это показывают тем, что значение для длины волны, при которой , сдвигается от значения для свободных электронов в длинноволновую область примерно на 248 нм. Подробный анализ поведения диэлектрической проницаемости для серебра дан в работах [30, 31, 21]. При больших длинах волн поведение электронов подобно поведению свободных электронов. В области, где имеются межзонные переходы, диэлектрическая функция ведет себя качественно как в случае полупроводников. Коллективные колебания в электронной системе проявляются в области, где значения функции энергетических потерь велики, а значения и - малы [29]. На рис.3 нами представлена функция энергетических потерь, соответствующая зависимостям и , приведенным на рис.1.

Здесь мы имеем дело не с чистым резонансом от свободных электронов, а с гибридным резонансом, связанным как электронами проводимости, так и электронами. В принципе, он может быть описан как обычный резонанс, но с введением зависимости от частоты [29].

Отметим, что для видимого и ИК диапазонов иногда применяют и скорректированную модель электронов Друдде, позволяющую, в определенной мере, правильно описывать экспериментальные данные по диэлектрической проницаемости в рассматриваемой ограниченной по длинам волн области. Так в работе [22] , где и - подбираемые параметры. Подобная зависимость, основанная на данных по оптическим константам для серебра [30], в конкретном виде: где с^-1 и с^-1, приведена в [31]. В нашем случае, исходя из (3) и (5), приходим к следующим выражениям для собственных частот аксиальных и азимутальных мод вытянутого сфероида:

, (7)

(8)

Соответствующие выражения для сплюснутого сфероида получаются с помощью указанной выше замены. Заметим, что дальнейшему упрощению в записи (7) и (8), подобному предпринятому в [27] для азимутальной моды, мешает присутствие в выражениях величин и .

В случае реальных образцов, содержащих большое количество сферических металлических частиц, взаимодействие между наводимыми на них внешним полем диполями приведет к сдвигу резонансной частоты и дополнительному уширению спектральной линии. Конкретные выражения для диэлектрической проницаемости такой среды с учетом диполь-дипольного взаимодействия были получены в работе [32] и уточнены в [33] для гранулярных пленок серебра с использованием выполненного в [34] определения действительной части диэлектрической проницаемости массивного металла с учетом межзонных переходов. Полученные результаты были применены к задаче об усилении люминесценции ионов европия для случая распределения наночастиц в объеме [6].

Наша острийная металлическая наноструктура представляет собой поверхность, на которой располагаются полусфероиды одинаковой формы. Поле , создаваемое на некотором диполе другими диполями за счет диполь-дипольного взаимодействия, описывается обычным выражением:

(9)

где - радиус-вектор на поверхности, соединяющий диполи и .

Мы провели расчеты собственных частот колебаний такой системы острий с учетом диполь-дипольного взаимодействия. Суммирование в выражении (9) было проведено в предположении, что острия расположены в узлах квадратной решетки с периодом, равным среднему расстоянию между порами в трековой мембране, используемой для получения острийной структуры (n- поверхностная плотность пор) [35]. В результате для частот аксиальной и азимутальной мод колебаний были получены, соответственно, следующие выражения:

(10)

(11)

где - удельный объем полусфероидов на поверхности.

Несомненный интерес представляет здесь различное направление сдвига собственных частот. Полосы поглощения (отражения) света, связанные с возбуждением аксиальных и азимутальных колебаний электронной плотности в сфероидах в результате диполь-дипольного взаимодействия должны сдвигаться, соответственно, в коротковолновую и длинноволновую области спектров. С точки зрения расчета это объясняется тем, что для аксиальных собственных колебаний в силу расположения полусфероидов на плоскости первый член в выражении (9) выпадает.

Полученный вывод можно сопоставить с имеющимися экспериментальными результатами. Так в работе [22] были измерены при нормальном падении света коэффициенты пропускания и отражения пленок аморфного кварца с включениями сферических наночастиц серебра. Наблюдалось, что для ансамбля частиц максимум полосы поглощения сдвигается от значения для частоты одной частицы в длинноволновую область, что рассматривалось как результат диполь-дипольного взаимодействия. В этом случае возбуждаются лишь колебания электронной системы в направлении параллельном поверхности пленки. Эту ситуацию описывает и выражение (11), в котором необходимо положить отношение a/b=1. Аналогичное сопоставление можно провести и с результатами работы [31], где также измерения велись при нормальном падении света.

Значительно больший интерес составит сравнение следствий из полученных нами выражений с результатами экспериментальной работы [36], в которой исследовалось отражение света именно острийными структурами, созданными с применением трековых мембран. Использовались серии образцов (серии далее обозначим номерами в скобках) с остриями со следующими полуосями и в нанометрах: 60 и 19 (1); 130 и 41 (2); 290 и 91 (3); 380 и 120 (4) и поверхностной плотностью острий во всех случаях равной см^-2. Это соответствовало коэффициентам s заполнения остриями поверхности (, s- площадь оснований всех острий на площади S), равным 1 (1), 5 (2), 24 (3) и 40% (4). Спектры отражения измерялись для p- и s- поляризованного света при углах падения (отражения) j =15, 45 и 75.

Как следует из анализа данных [36], в спектрах отражения для s-поляризации при всех углах падения света проявляется полоса, обусловленная возбуждаемыми азимутальными колебаниями электронной плотности в остриях, максимум которой при малых s расположен в области 350 нм. При увеличении коэффициента заполнения наблюдалось место смещение полосы в длинноволновую область. Учитывая, что линии во всех спектрах отражения достаточно широки, определим минимумы в спектрах отражения для рассматриваемых образцов при следующих длинах волн: 350 (1), 364 (2), 415 (3) и 600 нм (4).

Для случая p-поляризации при небольших отклонениях угла падения света от перпендикуляра к поверхности проявляется отражение, связанное с возбуждением как аксиальных, так и азимутальных плазмонных колебаний. Полосы в спектрах отражения, вызванные аксиальными колебаниями, значительно шире полос, связанных с азимутальными колебаниями, и, как и следовало ожидать, яснее проявляются при больших углах падения света. Так увеличение угла до 75 при s = 5% позволило полностью подавить азимутальные колебания. При небольшом коэффициенте s = 1%, когда отражение велико (около 70%), эта полоса для угла 75достаточно широка и имеет минимум, определенный в работе [36] как лежащий при 600 нм. С увеличением коэффициента заполнения полоса, связанная с аксиальными колебаниями электронной плотности в остриях сдвигается в область более коротких волн, максимумы которых по приведенным спектрам можно оценить лежащими при 600 (1), 520 (2), 460 нм (3) и 350 (4) нм.

В работе [36] такой разнонаправленный сдвиг полос в спектрах отражения был связан предположительно с возбуждением в острийных структурах резонансов более высоких порядков при высоких коэффициентах заполнения поверхности остриями. Покажем, что подобное поведение полос отражения достаточно хорошо объясняется проявлением диполь-дипольного взаимодействия между наводимыми в остриях диполями.

Для всех образцов a/b>1 (случай вытянутых полусфероидов) , 1.05, величины удельных объемов q » 210^-3(1), 310^-2(2), 0.14 (3) и 0.24 (4). Величина =1 (вакуум). Из выражений (7) и (8) можно определить конкретные численные значения и . Затем, из экспериментальных данных по частотной зависимости действительной части диэлектрической проницаемости серебра [18] можно найти соответствующие значения и . В результате, используя выражения (10) и (11) , получаем следующие собственные значения длин резонансных волн для соответствующих образцов: 494 (1), 480 (2), 330 (3) и 111 (4) нм; 344 (1), 347 (2), 435 (3) и 1030 (4) нм.

Рассчитанное нами значение 344 нм для λ_smq(1) достаточно близко к полученной из эксперимента величине- 350 нм (1). Выражение (7) правильно описывает и сдвиг полос с увеличением плотности острий в длинноволновую область.

При наибольшем коэффициенте заполнения, равном 40%, отражение сильно падает (до 5 % в максимуме поглощения), линия сильно уширяется и сдвигается далее в длинноволновую область спектра к 600 нм. Наша оценка дает 1030 (4) нм. Как отмечено в работе [34], для такого значения s вероятность парных перекрытий оснований острий достигает 80%.

Можно сделать вывод, что и выражение (8) правильно качественно описывает наблюденную в эксперименте картину. Большое расхождение длин волн для максимального значения s =40% в значительной мере можно приписать тем же причинам, что и для азимутальных колебаний.

При рассмотрении мы использовали модельное описание острий как полусфероидов, предполагалось регулярное распределение острий по поверхности и была использована скорректированная модель Друде. Тем не менее, учитывая, что экспериментально наблюденные полосы отражения достаточно широки, особенно для p-поляризованного света, а также то, что обычно используется неполяризованный свет, представляется вполне возможным использовать полученные выражения (7)-(11) для подбора необходимых геометрических размеров острий и их поверхностной плотности для получения усиления люминесценции для конкретного РЗИ.

Проведенный расчет в рамках модели полусфероидов качественно правильно описывает ситуацию (сдвиги линий в спектрах отражения и пр.). Однако для создания необходимых острийных наноструктур, имеющих плазмонные частоты в нужных для пракических целей частотных точках, необходимы полные расчеты с учетом реальной структуры и формы нанострий, включая радиус окончания, статистический разброс размеров и т.п. Это можно выполнить с использованием современных программ электродинамического моделирования, получивших широкое применение в расчетах СВЧ приборов.

3. Численное моделирование наноструктур произвольной формы

Для моделирования падения оптических световых волн на металлические поверхности со сложной структурой нами использован метод расчета во временной области (метод конечных разностей во временной области FDTD)

В решении данной конкретной тестовой задачи было отдано предпочтение программе CST MWS [39], поскольку она позволяет выполнить анализ падения плоской волны на бесконечную структуру, используя порты Флоке. Скорость решения и точность позволяет решать сложные научные задачи.

В этом случае можно рассчитать характеристики отражения и прохождения мощности через частотно-селективную поверхность, форму которой можно придать в виде штырей, впадин других резонансных структур. В этом случае для создания высокодобротной резонансной структуры, которая активно меняет частотный спектр оптической волны, падающей на нее, можно применять существенные наработки в области СВЧ и антенной техники, которые созданы к настоящему времени [41].


Рис. 5. а)Структура из полусфер, в) структура из цилиндрических резонаторов, с) структура из эллиптических неоднородностей.

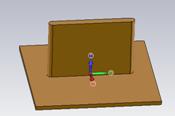
Рассмотрим структуру из острий с шаровым окончанием (рис. 5), на которую под разными углами падает плоская волна.

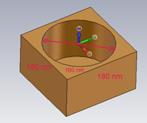
Для того, чтобы уменьшить объем пространства, в котором будет рассчитываться электромагнитное поле, выделим, как и раньше, повторяемые пространства, которые охватим периодическими граничными условиями. Так, если задано, что плотность 8*10⁸ см^-2 то можно выбрать площадку размером 320 nm на 320 nm, установить на нем отражающий объект.

Связь отдельных элементов подобна тому, как это происходит в антенных решетках, когда возбуждаемая вдоль оси Z волна может получить отклонение фронта распространения, благодаря сдвигу фаз ближнего поля, согласно разнице между ведущей и ведомой границе [41].

Закругления сверху конусов (рис. 5) имеют радиус 6.5 nm. При падении волны под определенным углом θ, часть энергии падает на конусы, которые выполняют роль диполей. Токи текут по плоской части структуры (рис. 5), а часть токов течет по конусам. Излучение этих токов приводит к изменению дифракции падающего поля.

Если задано, что острия посеяны с плотностью r_s=8*10⁸ см^-2, то для получения плотности s=5% один отражающий конус с нижним диаметром 80 nm нужно установить на площадку размером 320 nm на 320 nm. Высота равна 130 nm.

Между остриями, которые выполняют роль вторичных излучателей (монопольных антенн), существует связь. Эта связь описывает диполь-дипольное взаимодействие, которое существует в реальной модели.

Рис.6. Коэффициенты отражения плоской волны p-поляризации от структуры при 5% плотности острийных окончаний,

1 – угол падения 15º, 2-угол падения 45º, 3 – угол падения 75º .

На рис.6 приводятся рассчитанные характеристики острийной структуры для продольной волны (р-поляризации, когда вектор Е лежит в плоскости, перпендикулярной плоскости XY). При изменении поляризации моды канала Флоке, получаем частотные характеристики коэффициента отражения для волны s-поляризации.

Учитывая, что программа CST MWS [39] выполняет полный электродинамический расчет, т.е. учитывает, в том числе, диполь-дипольное взаимодействие, отражения и интерференцию между остриями, рассчитанные характеристики имеют более сложный характер и большое количество резонансов.

На рис. 6 показаны частотная зависимость коэффициента отражения от поверхности при падении волны с р-поляризацией. Отраженный сигнал имеет обе составляющие, и составляющую с p-поляризацией, и составляющую с s-поляризацией.

P-поляризацию имеет отраженная волна, которая пропорциональна длине острия по высоте. Эта поляризация приобретается при больших длинах волн. В же время, когда углы падения малые (волна падает почти нормально), то мощность составляющей, которая зависит от диаметра острия, становится более существенной.

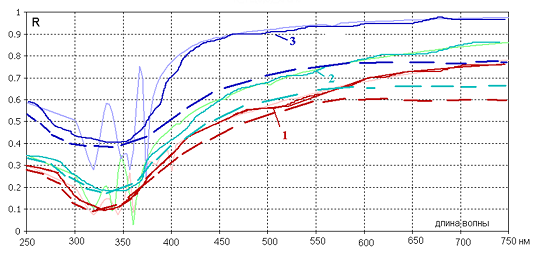
Рис.7. Коэффициенты отражения плоской волны s-поляризации от структуры при 5% плотности острийных окончаний,

1 – угол падения 15º, 2-угол падения 45º, 3 – угол падения 75º .

На рис. 6-7 приводятся, в виде пунктирных линий, экспериментальные зависимости, полученные в [36]. Можно видеть, что в расчетах подтвердилось физическое явление, обнаруженное в эксперименте: уменьшение мощности отражения в зависимости от угла падения (справа от точки А в расчете и точки B в эксперименте). Провал характеристики коэффициента отражения означает, что отраженный сигнал при малых углах падения (15° и 45°) получает s-поляризацию (1 и 2 зависимости на рис. 6).

С увеличением угла падения (75°) отраженный сигнал имеет и р-поляризацию и s-поляризацию (зависимость 3 на рис. 6).

Для зависимости 1 (15°) из рис. 6 имеем резонансную длину волны равную 350 нм. Это значение означает, что на этой длине волны возникает поверхностный плазмон.

Для зависимости 2 (угол падения 45°) эксперимент дает 330 нм (s-поляризация остается на месте 350 нм, но появляется другой провал, соответствующий р-поляризации 550 нм).

Для случая рис. 2 падающая волна имеет s-поляризацию. В этом случае отраженный сигнал имеет тоже s-поляризацию. Для углов падения 15° (кривая 1) расчетные и экспериментальные данные имеют значения 320 нм и 340 нм. Для угла падения 45° (кривая 2) расчетные и экспериментальные значения равны 350 нм и 330 нм. Для угла падения 75° (кривая 3) расчетные данные получили несколько значений 320 нм, 350 нм и 370 нм.

Расчеты для ряда плотностей расположения острийных окончаний на плоскости показывают, что минимум коэффициента отражения смещается в сторону больших длин волн. И при самых больших плотностях может достигнуть минимума при длине волны 500 нм (рис. 16). В заключении отметим, что расчеты были выполнены на современном двухядерном компьютере RAM=3 ГГб. Время расчета одной частотной точки порядка 30 мин.

4. Заключение

Проанализированы оптические характеристики металлических острийных наноструктур в рамках модели полусфероидов. Рассмотрено влияние диполь-дипольного взаимодействия на собственные частоты поверхностных плазмонов в остриях. Показано, что данная модель качественно правильно описывает поведение спектров отражения в зависимости от поляризуемости, углов падения электромагнитной волны, плотности острий. Данная модель может быть использована для оценки необходимых геометрических характеристик острийных структур для их получения.

Точные расчеты острийных структур с учетом всех геометрических характеристик (конусообразность, форма заострения и пр.) проводились с использованием метода FDTD. Показано, что численные расчеты правильно описывают экспериментальные данные. Это показывает реальные перспективы для совершенствования анализа и синтеза оптических систем.

Литература

1. B.R. Judd. Phys.Rev. 127, 750 (1962).

2. G.S. Ofelt. J.Chem.Phys. 37, 511 (1962).

3. Ch.K.Jorgensen, B.R. Judd. Mol.Phys. 8, 281 (1964).

4. S.F.Mason , R.D.Peacock , B.Stewart. Mol.Phys. 30, 1828 (1975).

5. D.A.Weitz , S.Garoff, C.D.Hanson, T.J.Gramila, J.I.Gersten. J.Lumin. 24/25, 83 (1981).

6. O.L. Malta , P.A.Santa-Cruz , G.F. De Sa, F.Auzel. J.Lumin. 33, 261 (1985).

7. Гигантское комбинационное рассеяние / Ред. Р.Ченг, Т.Фуртак. Мир, М. (1984). 484 с.

8. О.В.Уваров, А.Л. Васильев, А.С.Авилов, Г.А.Денисенко, Ж.Ф. Де Са. Кристаллография. 33, 1546 (1988).

9. G.A.Denisenko, L.D.Kislovskii, O.L.Uvarov, A.L.Vasil’ev, A.S.Avilov, B.F.Djurinskii, G.F.De Sa, O.L.Malta. Rev. Brasileira de Fisica. 19, 219 (1989).

10. F. Pelle F. Abstr. Rencontre Franco-Espanol sur la Chimie et Physique de l’Etat Solide. Abstracts .Carcans-Maubuisson, France (2000). Report C-14.

11. Г.Е.Малашкевич, Г.П.Шевченко, С.В.Сережкина, Г.А.Денисенко, П.П.Першукевич. Известия РАН, сер.физическая. 70, 1662 (2006).

12. Г.Е.Малашкевич, А.В.Семченко, А.А.Суходола, А.П.Ступак, А.В.Суходолов, Б.В.Плющ, В.В.Сидский, Г.А.Денисенко. ФТТ 50, 1408 (2008).

13. Г.А.Денисенко, В.А.Олейников, Г.Е.Малашкевич, А.П.Войтович, А.Г.Базылев, Б.В.Мчедлишвили, В.Стренк. ЖПС 62, 130 (1995).

14. G.A.Denisenko, G.E.Malashkevich, T.V.Tziganova, V.G.Galstyan, A.P.Voitovich, P.P.Pershukevich, I.I.Kalosha, A.G.Bazilev, B.V.Mchedlishvili, W.Stręk, V.A.Oleinikov. Acta Physica Polonica A 90, 121 (1996).

15. Г.Н.Флеров, В.С.Барашенков. УФН 114, 351 (1974).

16. S.N.Dmitriev, L.I.Kravets, N.V.Simakina, V.V.Sleptsov. Radiat. Meas. 25,723 (1995).

17. А.Н.Нечаев, В.В.Березкин, Г.С.Жданов Г.С. и др. В сб.: Трековые мембраны: синтез, структура, свойства и применения / Под ред. П.Ю.Апеля, Б.В.Мчедлишвили, М. (2004). С.42.

18. B.V.Mchedlishvili, V.V.Beryozkin, V.A.Oleinikov, A.I.Vilensky, A.B.Vasiliev. J.Membrane Sci. 79 285 (1993).

19. U.Kreibig, M.Vollmer. Optical properties of metal clusters. Springer-Verlag, Berlin, Heidelberg (1995). 531 p.

20. М.И.Гайдук, В.Ф. Золин, Л.С. Гайгерова. Спектры люминесценции европия. Наука, М. (1974). 195 с.

21. P.B. Johnson , R.W.Christy. Phys.Rev. B 6, 4370 (1972).

22. H. Mertens, J.Verhoeven, A.Polman, F.D.Tichelaar. Appl.Phys.Lett. 85 1317 (2004).

23. J.Gersten , A.Nitzan. J.Chem.Phys. 73, 3023 (1980).

24. U.Kreibig, C.v.Fragstein. Z.Phys. 224, 307 (1969).

25. A.Wokaun, J.P. Gordon, P.F.Liao. Phys.Rev.Lett. 28, 957 (1982).

26. Е.В.Гобсон. Теория сферических и эллипсоидальных функций. ИЛ, М. (1952).

27. A.Moussiaux , A.Ronveaux , A.Lucas. Can.J.Phys. 55, 1423 (1977).

28. E.A.Taft, H.R.Philipp. Phys.Rev. 121, 1100 (1961).

29. H.Ehrenreich, H.R.Philipp. Phys.Rev. 128, 1622 (1962).

30. E.D.Palik Handbook of Optical Constants of Solids. Academic, Orlando. (1985). 450 p.

31. L.A.Sweatlock, S.A.Maier, H.A.Atwater, J.J.Penninkhof, A.Polman. Phys.Rev. B 71, 235408 (2005).

32. W.Hampe. Z.Phys. 152, 476 (1958).

33. И.Н.Шкляревский, П.Л.Пахомов, Т.И.Корнеева. Опт. и спектр. 34, 729 (1973).

34. В.К.Милославский, Р.Г.Яровая. Опт. и спектр. 21, 708 (1966).

35. А.В.Митрофанов. Препринт 29, ФИАН, Москва (2003).

36. В.А.Олейников, К.В.Соколов, И.Р.Набиев. ЖПС. 59, 123 (1993).

37. Krenn J.R., Schider G., Rechberger W. et.al. // Apll. Phys.Lett. 2000. V.77. P.3379

38. Numerical Techniques For Microwave And Millimeter-Wave Passive Structures. Ed. by Tatsuo Itoh, N/Y. (1989). 707 pp.

39. [Электронный ресурс]: сайт производителя программы CST MWS. URL: www.cst.com

40. H. Yang, R. Mittra. FDTD Modeling of Metamaterials Theory and Applications. Artech House. (2009), 380 pp.

41. С.Е. Банков, А.А.Курушин. Электродинамика и техника СВЧ для пользователей САПР. М. (2008). 276 с. http://jre.cplire.ru/jre/library/3/toc.html.

42. G.A. Denisenko, Gutzeit E.M., Kurushin A.A. Electrodynamics Modeling of Nanosized Optical Systems. 4^th International Conference on Physics of Laser Crystals. Sudak, Crimea, 12-16 September 2010, Kharkiv-Sudak, p. OC10.
43. А.А. Курушин. Использование каналов Флоке для моделирования периодической наноструктуры. [Электронный ресурс] // Журнал радиоэлектроники. 2010. № 11. Режим доступа: http://jre.cplire.ru/jre/nov10/5/text.html